我爱学算法之—— 分治-归并

努力学习的小廉2025-10-25 15:06

一、排序数组

题目解析

这道题就是一个简单的排序数组（与分治-快排中排序数组那道题一样）

算法思路

这里就回顾一下归并排序，使用归并排序来解决这道题。

简单来说归并排序就分为两步：

  1. 递归划分数组
  2. 合并两个有序数组

合并两个有序数组：

归并排序中，划分数组是提供递归分治实现的；在整个代码逻辑中，我们只需要实现合并两个有序数组即可。

以升序排序为例：

  1. 定义两个指针cur1、cur2遍历两个数组（升序的）；定义一个tmp数组，用来记录排序完的数组。
  2. 谁小就将谁放到tmp数组中。
  3. 遍历完之后，如果cur1/cur2（其中一个）没有遍历完，就将其后面的元素一次放入数组tmp数组中。
  4. 最后，还原数组即可。

代码实现

cpp 复制代码 
class Solution {
public:
    void msort(vector<int>& nums, int left, int right) {
        if (left >= right)
            return;
        // 递归划分数组
        int mid = left + (right - left) / 2;
        msort(nums, left, mid);
        msort(nums, mid + 1, right);
        // 合并两个有序数组
        int sz = right - left + 1;
        int cur1 = left, cur2 = mid + 1;
        vector<int> tmp(sz);
        int i = 0;
        while (cur1 <= mid && cur2 <= right) {
            if (nums[cur1] <= nums[cur2])
                tmp[i++] = nums[cur1++];
            else
                tmp[i++] = nums[cur2++];
        }
        while (cur1 <= mid) {
            tmp[i++] = nums[cur1++];
        }
        while (cur2 <= right) {
            tmp[i++] = nums[cur2++];
        }
        // 还原数组
        for (i = 0; i < sz; i++) {
            nums[left + i] = tmp[i];
        }
    }
    vector<int> sortArray(vector<int>& nums) {
        msort(nums, 0, nums.size() - 1);
        return nums;
    }
};

二、交易逆序对的总数

题目解析

这道题，给定一个数组nums，要我们求出这个数组nums中的逆序对个数。（逆序对就是左边的数大于右边的数）

算法思路

解法一：暴力枚举

枚举出数组nums中的所有的二元组，判断是否是逆序对，然后统计逆序对的个数。

时间复杂度O(n^2)

解法二 ：归并排序

第一次看到这道题，可能会很疑惑，这跟归并排序有什么关系呢？

归并排序是先进行数组划分，然后再合并数组中有序的两部分。

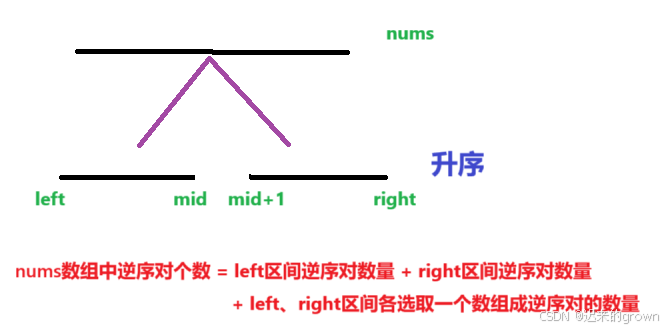
数组nums中的逆序对个数 = 左边期间逆序对个数 + 右边区间逆序对个数 + 左区间选一个数、右区间选一个数组成逆序对的个数

而在归并排序中，是要进行合并数组中两个有序的部分的，合并的过程不就是从left、right区间各选取一个数进行比较大小吗？

所以，在遍历过程中，left、right区间中的逆序对个数通过递归返回值过去；我们只需在合并两个有序数组的过程中，统计left、right区间各选取一个数能组成逆序对的数量。

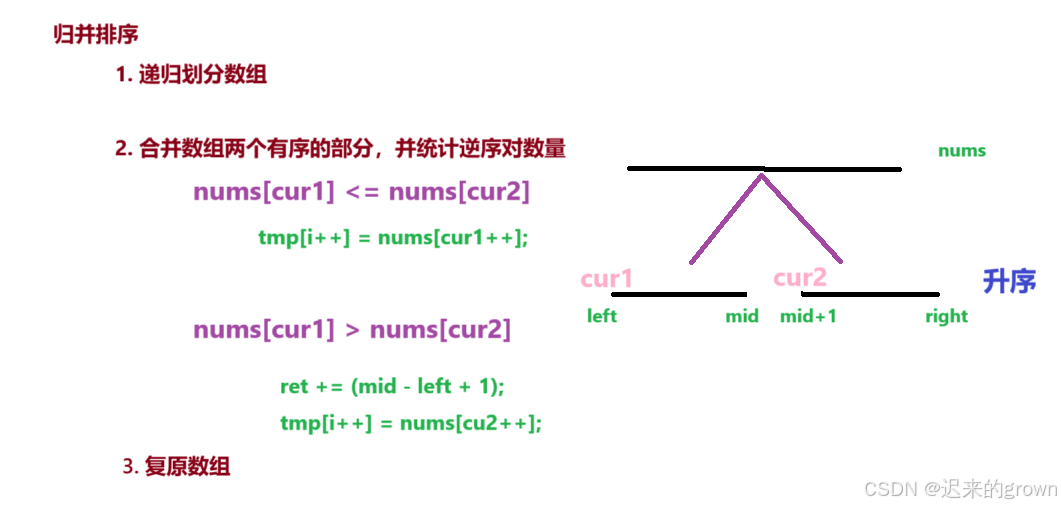
合并两个有序的数组，并统计逆序对数量 （这里按升序排序）：

定义cur1遍历left区间、cur2遍历右区间。

  • nums[cur1] <= nums[cur2] ：tmp[i++] = nums[cur1++]

  • nums[cur1] > nums[cur2] ：ret += (mid - cur1 + 1); tmp[i++] = nums[cur2++]

    因为数组是升序排序的，nums[cur1] > nums[cur2]，所以[cur1,mid]区间的所有元素都大于nums[cur2]都能和nums[cur2]组成一个逆序对。

因为这里是归并排序，在统计逆序对个数时，left区间和right区间是有序的；且left区间中任意一个元素一定在right中元素的左边。


这里使用升序排序，在合并两个有序数组部分时：

如果nums[cur1] > num[cur2]，区间[cur1, mid]中的所有元素都大于nums[cur2]；以nums[cur2]为右边值就存在mid-cur1+1个逆序对。

代码实现

cpp 复制代码 
class Solution {
public:
    int msort(vector<int>& nums, int left, int right) {
        if (left >= right)
            return 0;
        int mid = left + (right - left) / 2;
        int ln = msort(nums, left, mid);
        int rn = msort(nums, mid + 1, right);
        // 合并两个有序数组、并统计逆序对数量
        int cnt = 0, sz = right - left + 1;
        vector<int> tmp(sz, 0);
        int cur1 = left, cur2 = mid + 1;
        int i = 0;
        while (cur1 <= mid && cur2 <= right) {
            if (nums[cur1] <= nums[cur2])
                tmp[i++] = nums[cur1++];
            else {
                cnt += (mid - cur1 + 1);
                tmp[i++] = nums[cur2++];
            }
        }
        while (cur1 <= mid)
            tmp[i++] = nums[cur1++];
        while (cur2 <= right)
            tmp[i++] = nums[cur2++];
        // 复原数组
        for (i = 0; i < sz; i++) {
            nums[left + i] = tmp[i];
        }
        return ln + rn + cnt;
    }
    int reversePairs(vector<int>& record) {
        int ret = msort(record, 0, record.size() - 1);
        return ret;
    }
};

三、计算右侧小于当前元素的个数

题目解析

这道题，和上一道逆序对的题可以说非常相似，逆序对那道题是让我们求逆序对的总数；

而这道题，则是让我们求出某一个位置右边有多少小于该位置的值的；也就是以某一位置为左边值，能组成逆序对的个数。

算法思路

对于这道题，整体思路是和求逆序对总数是相同的。

暴力解法：遍历数组，枚举所有的二元组，求出每一个位置右侧小于自己的元素个数。

分治-归并：

和求逆序对一样，但是这道题要注意要求出每一个位置右侧有多少元素小于自己（也就是以某一个位置为左边值，能形成逆序对的个数）

所以，在进行归并排序的过程中，我们不仅要对数组进行排序，并且还要维护下标。

这里使用降序排序，合并两个有序的数组部分时：

如果nums[cur1] > nums[cur2]时，区间[cur2, right]中的所有元素都能和nums[cur1]形成逆序对，此时找到nums[cur1]对应原始数组中下标，统计逆序对个数即可。

维护nums中每一个元素的值，以及它的原始下标；在排序的过程中，不仅要排序数组，还是更修对应的原始下标

代码实现

cpp 复制代码 
class Solution {
public:
    void msort(vector<int>& ret, vector<int>& nums, vector<int>& index,
               int left, int right) {
        if (left >= right)
            return;
        int mid = left + (right - left) / 2;
        msort(ret, nums, index, left, mid);
        msort(ret, nums, index, mid + 1, right);
        int sz = right - left + 1;
        int cur1 = left, cur2 = mid + 1, i = 0;
        vector<int> tmp_n(sz), tmp_i(sz);
        while (cur1 <= mid && cur2 <= right) {
            if (nums[cur1] <= nums[cur2]) {
                tmp_n[i] = nums[cur2];
                tmp_i[i++] = index[cur2++];
            } else {
                ret[index[cur1]] += (right - cur2 + 1);
                tmp_n[i] = nums[cur1];
                tmp_i[i++] = index[cur1++];
            }
        }
        while (cur1 <= mid) {
            tmp_n[i] = nums[cur1];
            tmp_i[i++] = index[cur1++];
        }
        while (cur2 <= right) {
            tmp_n[i] = nums[cur2];
            tmp_i[i++] = index[cur2++];
        }
        for (int i = 0; i < sz; i++) {
            nums[left + i] = tmp_n[i];
            index[left + i] = tmp_i[i];
        }
    }
    vector<int> countSmaller(vector<int>& nums) {
        int n = nums.size();
        vector<int> ret(n, 0), index(n);
        for (int i = 0; i < n; i++)
            index[i] = i;
        msort(ret, nums, index, 0, n - 1);
        return ret;
    }
};

四、翻转对

题目解析

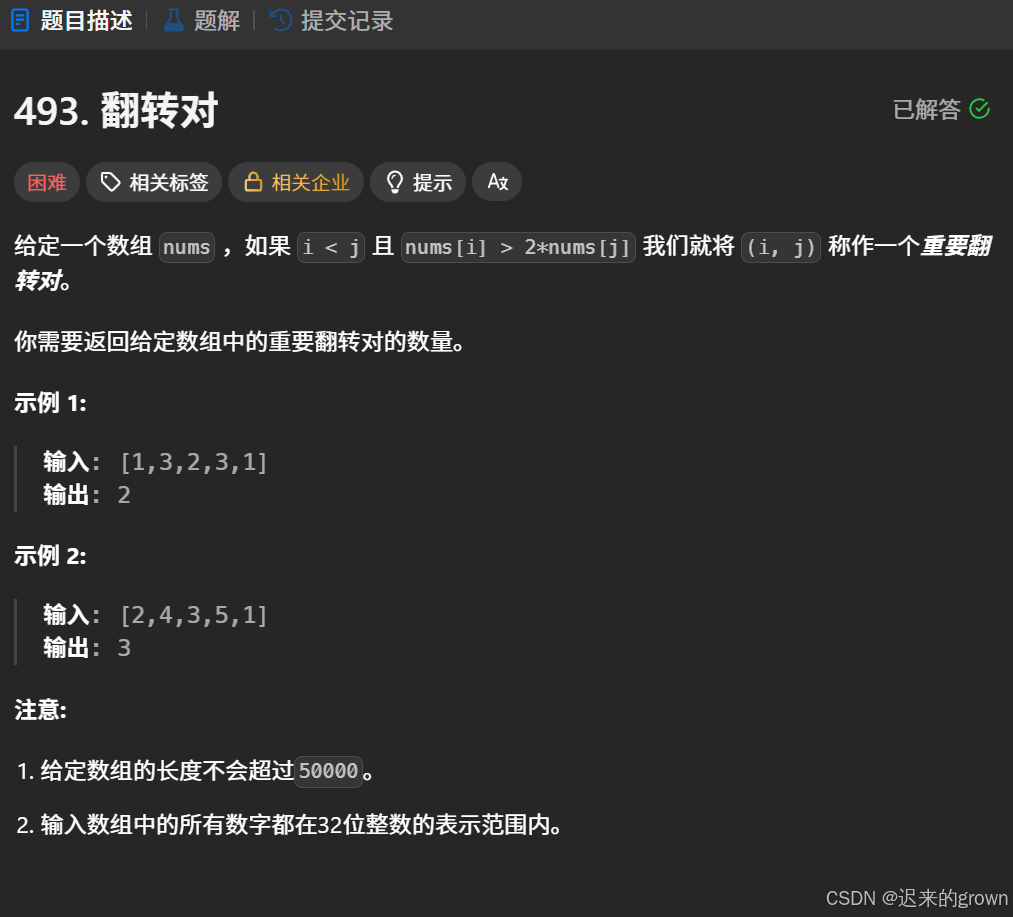
这道题和上述逆序对的题稍稍不一样，这里如果i<j并且nums[i] > 2*nums[j]，(i,j)就是一个重要翻转对。

给定一个数组nums要我们求出数组中重要翻转对的数量。

算法思路

这道题的整体思路和上述是一模一样的，还是在归并排序的过程中去求重要翻转对的个数。

在分治-归并排序的过程，合并两个有序数组时，可以保证左边区间中的元素下标都是小于右边区间元素的下标的；

所以，只需要统计坐标区间中任意元素和右边区间中的任意元素，满足nums[i] > 2*nums[j]即可。

而两个数组区间还是有序的 ：（降序排序 ）如果nums[i] >nums[j]*2，则区间[j, right]中所有元素都可以和元素i形成一个重要翻转对。

至于左、右区间内的重要翻转对个数，在递归的过程中求出即可。

这里因为判断重要翻转对的条件时nums[i] > 2*nums[j]，而排序数组的条件是nums[i] > nums[j]。

所以，在归并排序的过程中，要先统计重要翻转对的个数，再合并两个有序的数组部分。

代码实现

cpp 复制代码 
class Solution {
public:
    int msort(vector<int>& nums, int left, int right) {
        if (left >= right)
            return 0;
        int mid = left + (right - left) / 2;
        int ln = msort(nums, left, mid);
        int rn = msort(nums, mid + 1, right);
        int cnt = 0, cur1 = left, cur2 = mid + 1;
        while (cur1 <= mid && cur2 <= right) {
            if (nums[cur1] <= 2 * (long long)nums[cur2])
                cur2++;
            else {
                cnt += (right - cur2 + 1);
                cur1++;
            }
        }
        int sz = right - left + 1, i = 0;
        cur1 = left, cur2 = mid + 1;
        vector<int> tmp(sz);
        while (cur1 <= mid && cur2 <= right) {
            if (nums[cur1] <= nums[cur2])
                tmp[i++] = nums[cur2++];
            else
                tmp[i++] = nums[cur1++];
        }
        while (cur1 <= mid)
            tmp[i++] = nums[cur1++];
        while (cur2 <= right)
            tmp[i++] = nums[cur2++];
        for (i = 0; i < sz; i++)
            nums[left + i] = tmp[i];
        return cnt + ln + rn;
    }
    int reversePairs(vector<int>& nums) {
        return msort(nums, 0, nums.size() - 1);
    }
};

本篇文章到这里就结束了，感谢支持

我的博客即将同步至腾讯云开发者社区，邀请大家一同入驻：https://cloud.tencent.com/developer/support-plan?invite_code=2oul0hvapjsws

相关推荐
上去我就QWER17 小时前
Qt快捷键“魔法师”：QKeySequence
开发语言·c++·qt
将编程培养成爱好20 小时前
C++ 设计模式《外卖骑手状态系统》
c++·ui·设计模式·状态模式
猿太极20 小时前
设计模式学习(3)-行为型模式
c++·设计模式
cynicme1 天前
力扣3228——将 1 移动到末尾的最大操作次数
算法·leetcode
熬了夜的程序员1 天前
【LeetCode】109. 有序链表转换二叉搜索树
数据结构·算法·leetcode·链表·职场和发展·深度优先
随意起个昵称1 天前
【递归】二进制字符串中的第K位
c++·算法
mjhcsp1 天前
C++ 循环结构：控制程序重复执行的核心机制
开发语言·c++·算法
立志成为大牛的小牛1 天前
数据结构——四十一、分块查找(索引顺序查找)（王道408）
数据结构·学习·程序人生·考研·算法
xier_ran1 天前
深度学习：RMSprop 优化算法详解
人工智能·深度学习·算法
地平线开发者1 天前
不同传感器前中后融合方案简介
算法·自动驾驶
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03BongoCat - 跨平台键盘猫动画工具04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05Linux下V2Ray安装配置指南06综合整理：pdf预览显示：你尝试预览的文件可能对你的计算机有害。如果你信任此文件以及其来源，请打开此文件以看其内容，如何解决以正常预览文件07jdk21下载、安装（Windows、Linux、macOS）08智能库存管理的需求预测模型：从业务痛点到落地代码的完整实践09Labelme从安装到标注：零基础完整指南10使用国内镜像网站在线下载安装Qt（解决官网慢的问题）——Qt