文章目录
一、读题
题目来源：https://leetcode.cn/problems/container-with-most-water/description/
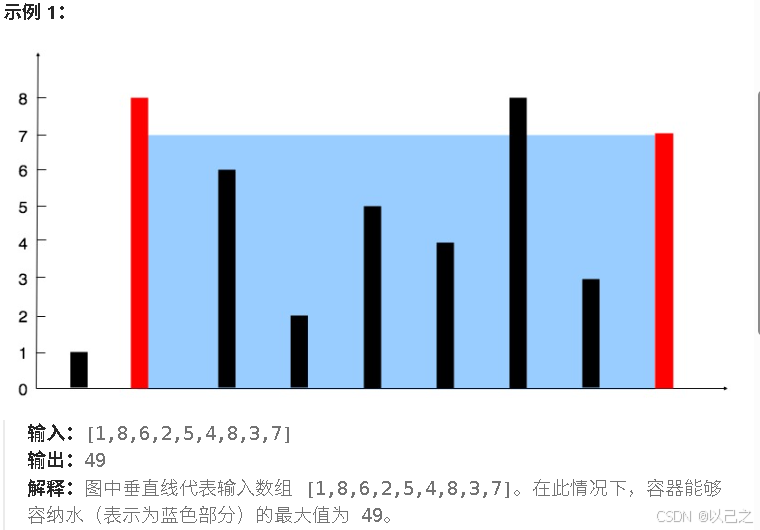
但看题目的讲解其实看的很懵逼，但是搭配示例看题目就很明确了，给定一个数组，根据数据的大小和宽度构成最大的容量，其实这一道题目本质上是水桶效应。
结果就是将最大的容量返回
二、算法思路
大家看到这个题目的第一想法肯定是暴力，直接来两个for循环遍历，把所有的结果都找出来，然后从中找最大值即可，但是我们仔细看，这一道题目的难度是中等，那么暴力ac的可能性就很小啊了，当然主包看到题目的第一想法也是暴力哈哈哈。
主包的思路是双指针，我们可以通过一个两数相乘来找思路。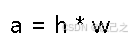
我们都知道在乘法里面，结果的大小和相乘数的大小息息相关，如果h减小w不变，那么a肯定减小，响应的w减小也是如此，唯一让a变大的可能性就是h增大，或者是w增大，当然一个增大一个减小也是有可能会导致a增大的，我们不排除这个可能性
现在我们再来看题，看我们的暴力思路，暴力的思路是通过一个数来乘以剩下的全部数据来排除一个数，就是先用1乘以其他的数据，乘完之后就可以将1排除，继续从8开始依次往后乘，一个一个的减少数据量，知道数据量最终为0。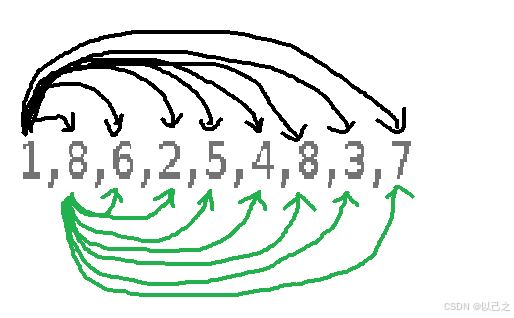
那么我们的主要思路就是减少数据量，而容积的大小和宽度高度这两个有关，那么我们可以一开始就举例最大的宽度来进行计算。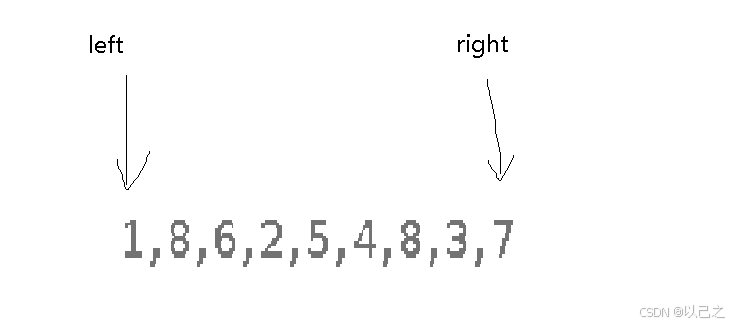
当我们计算完1和7的容积后，接下来我们应该是减少宽度，那么就是left++或者是rught--，那么我们应该选择那个呢？我们来思考一下，题目找的是最大的容积，那么我们计算完1和7的容积后是不是应该找大于1和7的容积呢？答案是肯定的，那么当宽度减小了，我们应该找高度增大的数据，只有在一个减小的情况下另外一个增大才有可能使得结果增大，因此我们应该left++，因为根据水桶效应，最大容积和最小的高度是直接关系，因此在1和7当中我们应该改变1，将1改变，即便我们不知道接下来是否是一定增大的，但是都有一定的概率要大于1，那么计算结果就有可能增大
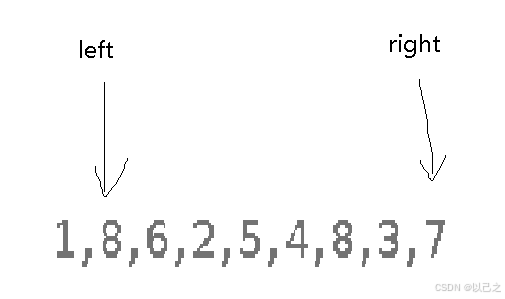计算完后接下来还是找高度增大的，那么就是right--；以此类推，直到两个指针相遇即可。这样子我们可以减少判断比当前两个指针的容积小的情况，只找有可能容积会增大的情况，那么在宽度减小的情况下，就只能将当前最低高度改变才会有可能增大容积
大家可能会觉得奇怪，这样子不会错过最大值吗？因为我们虽然是将较小的那个高度进行移动，那么会不会有可能将最大值错过，这个是肯定不会的，这个涉及到单调性，如果我们移动了较小高度了之后会保留当前的较大高度，每次移动都会保留当前的较大高度，根据水桶效应，容积的最大值是根据最小高度决定的，因此我们就可以通过不断提高最小高度来增大容积，那么我们就选择将较小的那个数字进行变化，保留较大值，那么每次我们都会将最大值拿到，因此较大值我们一定都遍历过，那么结果肯定在这其中。
三、代码实现：
sql
class Solution {
public int maxArea(int[] height) {
int i= 0;
int j = height.length - 1;
int ans = 0;
while(i < j){
int ret = (j - i) * Math.min(height[i] , height[j]);
ans = Math.max(ans , ret);
if(height[i] > height[j] ) {
j--;
} else {
i++;
}
}
return ans;
}
}各位佬，如果有什么更加高效的算法欢迎评论区讨论，指导一下主包进步，大家一起共勉