06_决策树 - 技术栈

文章目录

[1 概述](#1 概述)
[2 决策树工作流程](#2 决策树工作流程)
- [2.1 特征选择](#2.1 特征选择)
- - [2.1.1 信息增益与 ID3](#2.1.1 信息增益与 ID3)
  - [2.1.2 信息增益率与 C4.5](#2.1.2 信息增益率与 C4.5)
  - [2.1.3 基尼指数与 CART](#2.1.3 基尼指数与 CART)
- [2.2 数据分裂](#2.2 数据分裂)
- [2.3 决策树剪枝](#2.3 决策树剪枝)
[3 API 使用](#3 API 使用)

1 概述

决策树（Decision Tree）是一种基于树形结构的算法，根据一系列条件判断逐步划分数据，缩小范围，最终得出预测结果。决策树由 4 部分组成：

根节点：树的节点，包含所有数据
内部节点：表示特征上的判断条件
分支：根据判断条件分出的路径
叶子节点：最终分类或回归的结果

决策树适用于需要规则化、可解释性和快速决策的场景，尤其在数据特征明确、样本量适中的情况下表现良好。在复杂任务中，它常作为基模型，与集成学习结合（如随机森林、梯度提升树）以提升性能。

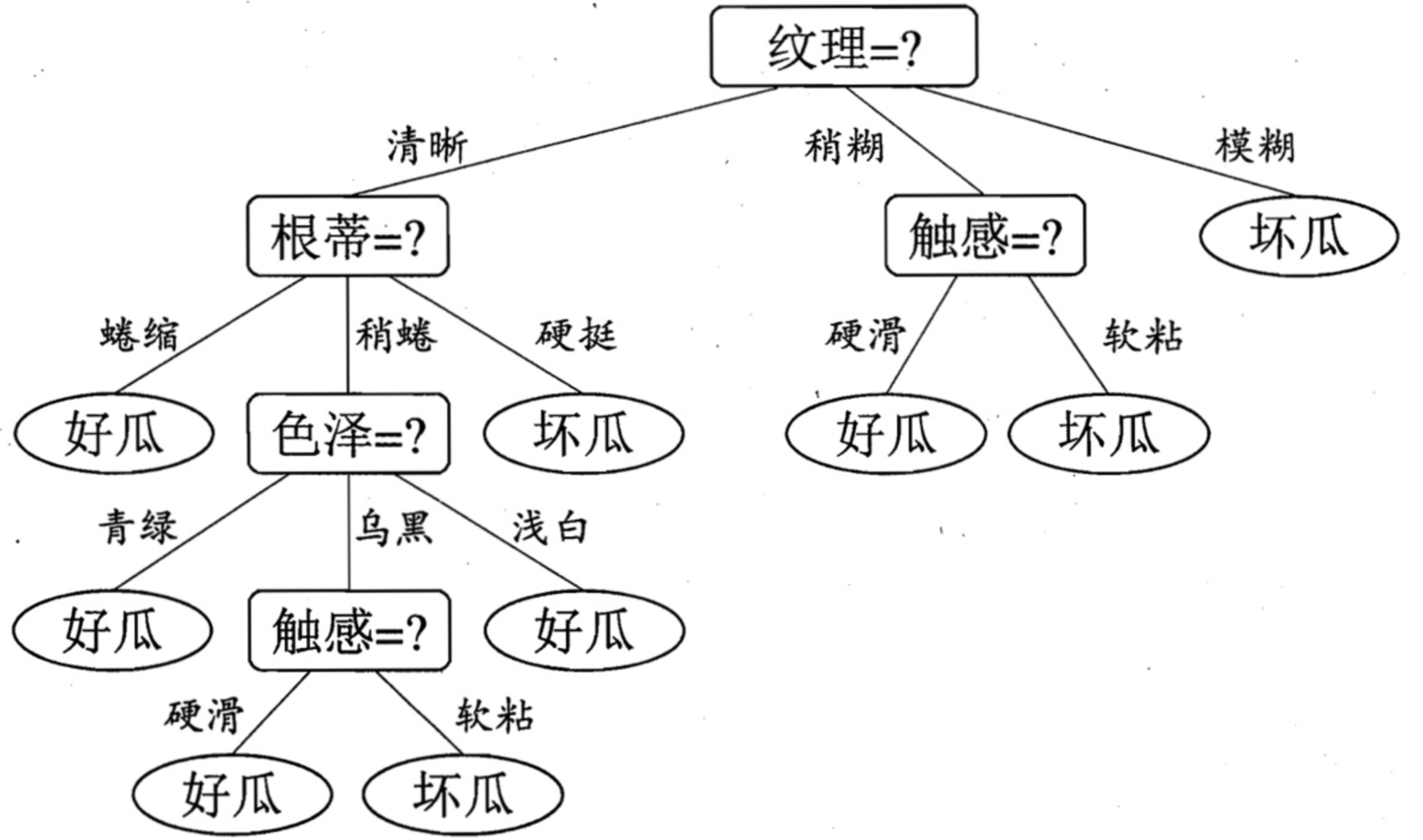
2 决策树工作流程

训练决策树模型有三个核心的步骤：特征选择、决策树构建和决策树剪枝。

递归选择最优特征，并根据该特征对训练数据进行划分，使得对各个子数据集有一个最好的分类。

首先构建根结点，将所有训练数据都放在根结点。
选择一个最优特征，按照这一特征将训练数据集划分成子集，使得各个子集有一个在当前条件下最好的分类。
如果这些子集已经能够被基本正确分类，那么构建叶结点，并将这些子集分到所对应的叶结点中去；如果还有子集不能被基本正确分类，那么就对这些子集选择新的最优特征，继续对其进行划分并构建相应的结点。
如此递归直至所有训练数据子集被基本正确分类，或者没有合适的特征为止。

最后每个子集都被分到叶结点有了明确的类，这就生成了一棵决策树。这样生成的决策树对训练数据有很好的分类能力，但可能发生过拟合现象。因此需要对已生成的树进行剪枝，将树变得更简单，从而使它具有更好的泛化能力。

2.1 特征选择

特征选择在于选取对训练数据具有分类能力的特征，这样可以提高决策树学习的效率。

如果一个特征能够使得分类后的分支结点尽可能属于同一类别，即该结点有着较高的纯度（purity），那么该特征对数据集而言就具备较强的分类能力。

通常选择的准则有信息增益、信息增益率和基尼指数

2.1.1 信息增益与 ID3

信息熵（entropy）是度量样本集合"纯度"的一个指标，当前样本集合 D D D 中共有 k k k 种类别，第 i i i 类样本样本的比例（也就是出现概率）为 p k p_k pk，则 D D D 的信息熵 定义为：
E n t ( D ) = − ∑ i = 1 k p i l o g 2 p i Ent(D) = -\sum_{i = 1}^{k} p_i\,log_2\,p_i Ent(D)=−i=1∑kpilog2pi

不难发现，信息熵越小， D D D 的纯度越大。可以得出， E n t ( D ) Ent(D) Ent(D)的最小值为 0，最大值为 l o g 2 k log_2k log2k。

直接以信息熵为基础，计算当前划分对信息熵所造成的变化，也就是信息增益（information gain） ，衡量的是当前划分对信息的不确定性减少的贡献程度。公式为 划分前的信息熵 - 划分后的信息熵 。
G a i n ( D , A ) = E n t ( D ) − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ E n t ( D v ) \mathrm{Gain}(D,A)=\mathrm{Ent}(D)-\sum_{v=1}^{V}\frac{|D_v|}{|D|}\mathrm{Ent}(D_v) Gain(D,A)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)

可以看出，划分后的信息熵表达的是在给定特征 A A A 的条件下，数据集 D D D 的不确定性，称为条件熵 ：
E n t ( D ∣ A ) = ∑ v = 1 V ∣ D v ∣ ∣ D ∣ E n t ( D v ) Ent(D|A)=\sum_{v=1}^{V}\frac{|D_v|}{|D|}\mathrm{Ent}(D_v) Ent(D∣A)=v=1∑V∣D∣∣Dv∣Ent(Dv)

特征 A A A 的取值： a 1 , a 2 , . . . a v {a_1, a_2,...a_v} a1,a2,...av，共有 V 个
D v D_v Dv： D D D 在特征 A A A 上取值为 a v a_v av 的样本子集
∣ D v ∣ D \frac{|D_v|}{D} D∣Dv∣：取值为 a v a_v av 的样本比例，第 v v v 个分支的权重，样本越多越重要
E n t ( D v ) Ent(D_v) Ent(Dv)：子集 D v D_v Dv 的信息熵

ID3 算法就是基于信息增益进行特征选择的。

2.1.2 信息增益率与 C4.5

信息增益作为划分准则时，倾向于筛选性强的特征，极端来看每个特征值只对应一个结果，那么结果就够纯，所以信息增益会倾向于选择取值较多的特征。

信息增益率（information gain ratio） 可以对这一问题进行校正：
G a i n r a t i o ( D , A ) = G a i n ( D , A ) I V ( A ) \mathrm{Gain_ratio}(D,A)=\frac{\mathrm{Gain}(D,A)}{\mathrm{IV}(A)} Gainratio(D,A)=IV(A)Gain(D,A)

其中 I V ( A ) IV(A) IV(A) 为：
I V ( A ) = − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ log ⁡ 2 ∣ D v ∣ ∣ D ∣ {IV}(A)=-\sum_{v=1}^{V}\frac{|D_{v}|}{|D|}\log_{2}\frac{|D_{v}|}{|D|} IV(A)=−v=1∑V∣D∣∣Dv∣log2∣D∣∣Dv∣
I V ( A ) IV(A) IV(A) 表述的基本思想是特征 A A A 的取值信息熵，取值数目越多，则 I V ( A ) IV(A) IV(A) 取值越大。

信息增益率希望选择的是：

信息增益尽可能大
特征取值尽可能少

C4.5 算法就是基于信息增益比进行特征选择的，但不是仅仅参考信息增益比，而是采用了启发式方法，会在避免取值较多的特征和避免信息增益过小之间找到平衡。

2.1.3 基尼指数与 CART

样本 D D D 有 k k k 种类别，样本属于第 k k k 种类别的概率为 p k p_k pk，那么两次抽到的是同一类别的概率为 p k 2 {p_k}^2 pk2，一共 k k k 种类别求和得到抽到任一同样类别的概率，用 1 减去这个概率，反映的是从样本 D 中任取两个样本，其类别标签不一致的概率 。
G i n i ( D ) = 1 − ∑ k = 1 n p k 2 Gini(D) = 1 - \sum_{k=1}^{n}{p_{k}}^{2} Gini(D)=1−k=1∑npk2

该值称为基尼指数（Gini index），基尼指数越大样本集合的不确定性也越大，这与信息熵相似。

属性 A 的基尼指数为：
G i n i _ i n d e x ( D , A ) = ∑ v = 1 V ∣ D v ∣ ∣ D ∣ G i n i ( D v ) Gini\index(D, A) = \sum{v=1}^{V}\frac{\lvert D_{v} \rvert}{\lvert D \rvert}Gini(D_{v}) Gini_index(D,A)=v=1∑V∣D∣∣Dv∣Gini(Dv)

和特征熵类似，根据特征 A 的取值，将数据集分为 V 个子集，分别计算每个子集的基尼指数，按照权重（占比）进行求和。

CART 算法就是基于基尼指数进行特征选择的，CART 既可以生成分类树，也可以生成回归树。

在回归问题中面对的特征是连续值，可以通过遍历特征所有可能的取值，找到切分点 x \small{x} x 让切分后的子集在信息增益比或基尼指数方面达到最优，在数据分裂时以 x \small{x} x 为分界点将数据划分为 D 1 \small{D_{1}} D1 和 D 2 \small{D_{2}} D2 两个子集，其中 D 1 \small{D_{1}} D1 包含特征值小于等于 x \small{x} x 的样本， D 2 \small{D_{2}} D2 包含特征值大于 x \small{x} x 的样本。

2.2 数据分裂

通过上述准则选定特征后就要进行数据分裂，根据选定特征将数据集分成两个或多个子集，每个子集对应于特征的不同取值。递归对每个子集重复特征选择和数据分裂的动作，直到满足停止条件。

常见的停止条件：

树达到预设的深度
当前结点的样本数量少于预设的阈值
结点上所有样本属于同一个类别
信息增益或 Gini 指数的变动低于某个阈值

2.3 决策树剪枝

剪枝可以减少树结构的复杂性，避免过拟合的风险，提升泛化能力。

预剪枝（pre-pruning）：在构建决策树的过程中设置一些限制条件（上一节中罗列了常见停止条件）提前停止树的生长，避免生成过于复杂的树，但是可能存在欠拟合的风险，因为过早停止分裂可能会遗漏潜在的重要决策规则。
后剪枝（post-pruning）：后剪枝是在决策树构建完成后，通过评估和移除一些不必要的分支来简化树结构。在减少过拟合风险的同时，还能较好的保留对数据的拟合能力，但是计算量较大，而且如果没有合适的验证集，剪枝效果就会受到影响。

3 API 使用

sklearn 中的基于 CART 算法分别实现了 DecisionTreeClassifier 和 DecisionTreeRegressor 来分别解决分类和回归问题。

python 复制代码

from sklearn.tree import DecisionTreeClassifier, DecisionTreeRegressor

model1 = DecisionTreeClassifier()
model2 = DecisionTreeRegressor()

criterion：特征选择（数据分裂质量评估）的标准，可以选择 'gini'或 'entropy'，前者代表基尼指数，也是默认值，后者代表信息增益。
max_depth：树的最大深度，默认值为 None，如果不设置该参数，会存在过拟合风险。
min_samples_split：一个内部结点再次分裂所需的最小样本数，默认值为 2。这个参数可以设置为整数表示最小样本数，也可以设置为浮点数，表示占总样本数的比例。
min_samples_leaf：叶结点所需的最小样本数，默认值为 1。将该参数设置为较大的值可以平滑模型，降低过拟合风险。这个参数也可以设置为整数或浮点数，道理同上。
max_features：用于最佳分裂的特征数，默认值为 None。这个参数可以设置为整数，表示选择固定数量的特征；可以设置为浮点数，表示选择特征的比例；可以设置为字符串，'auto'和 'sqrt'表示将总的特征数量求平方根，用平方根的值作为选择特征的数量，'log2'表示将总的特征数量求对数，用对数值作为选择特征的数量。
class_weight：指定类别的权重，用于处理类别不平衡问题，默认值为 None。可以用字典的方式手动设置每个类别的权重，也可以使用 'balanced'让模型自动调整。
splitter：选择分裂结点的策略，默认值为 'best'，表示最佳分裂，还有一个取值是 'random'，表示随机分裂。
max_leaf_nodes：限制叶结点的最大数量，可以防止树结构过于复杂。
min_impurity_decrease：结点分裂所需的最小不纯度降低值，任何结点只有在不纯度减少超过此值时才会进行分裂。
ccp_alpha：成本复杂度剪枝中的 α \small{\alpha} α参数值。这个参数用于控制后剪枝中成本复杂度计算公式中 α \small{\alpha} α的值。较小的 α \small{\alpha} α值允许更复杂的树，而较大的 α \small{\alpha} α值倾向于选择更简单的树。通过调整 α \small{\alpha} α，可以找到一个最佳的复杂度和误差之间的平衡点。

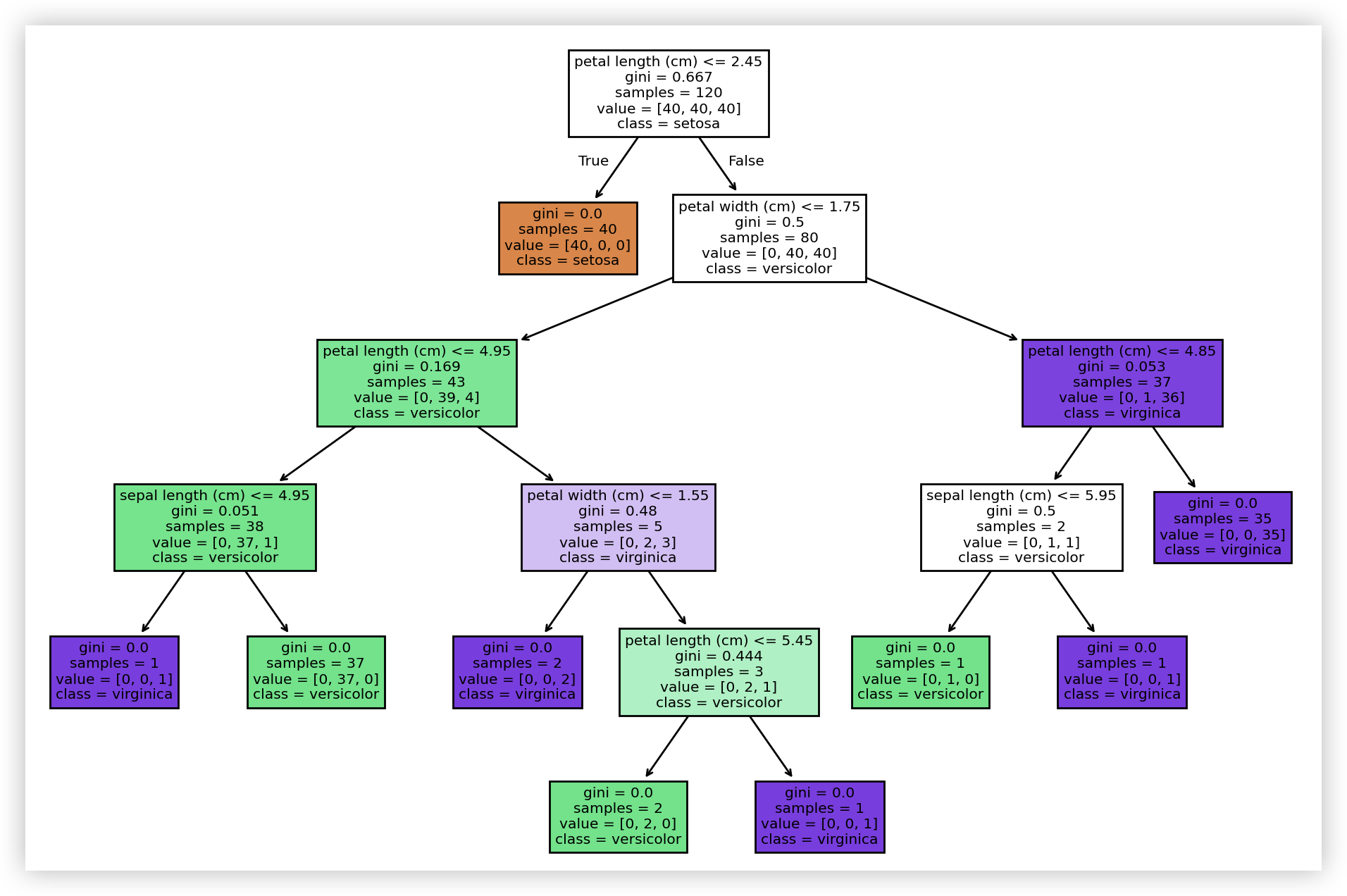
通过以下代码可以可视化决策树：

python 复制代码

from sklearn.tree import plot_tree

plot_tree(
    decision_tree=model,               # 决策树模型
    feature_names=iris.feature_names,  # 特征的名称
    class_names=iris.target_names,     # 标签的名称
    filled=True                        # 用颜色填充
)