此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下:
- 原课程视频链接:[双语字幕]吴恩达深度学习deeplearning.ai
- github课程资料,含课件与笔记:吴恩达深度学习教学资料
- 课程配套练习(中英)与答案:吴恩达深度学习课后习题与答案
本篇为第一课第四周的课程练习部分的讲解。
1.理论习题
【中英】【吴恩达课后测验】Course 1 - 神经网络和深度学习 - 第四周测验
同样,这是本周理论部分的习题和相应解析,博主已经做好了翻译和解析工作。
这里单独选出一道题如下:
向量化允许您在L层神经网络中计算前向传播,而不需要在层(l = 1,2,...,L)上显式的使用for-loop(或任何其他显式迭代循环),正确吗?
答案:错误
通过这道题,我们来总结一下:
向量化后的神经网络,到底省去了哪些部分的显式循环?又有哪些循环始终不能省去?
1.1 非向量化的神经网络需要定义哪些循环?
在没有向量化之前,前向传播过程通常包含以下显式循环:
| 循环类型 | 作用对象 | 描述 |
|---|---|---|
| 轮次循环(Epoch) | 整个训练集反复训练的次数 | 为了不断优化参数,必须多次重复训练整个训练集,每一轮称为一个 Epoch。 |
| 批次循环(Batch) | 每一个批次 | 若使用小批次梯度下降,则每轮训练需要对所有批次依次执行前向和反向传播。(一批次训练所有样本则不需此行) |
| 样本循环 | 每个样本 | 对训练集中的每个样本单独计算前向传播和损失(在未向量化时存在)。 |
| 层循环 | 每一层 | 逐层计算:当前层的输出依赖上一层输出,因此必须按顺序执行,无法并行消除。 |
| 层内神经元循环 | 当前层的每个神经元 | 计算当前层每个神经元的加权和与激活(可被矩阵运算替代)。 |
| 特征循环 | 某个神经元内部所有输入特征 | 对输入特征逐一乘权重再求和,即实现一次点乘(可向量化消除)。 |
1.2 向量化的神经网络省去了哪些循环?
向量化后,再次总结如下:
| 循环类型 | 是否被消除 | 原因说明 |
|---|---|---|
| 轮次循环(Epoch) | 无法消除 | 每一轮训练都需更新参数,是梯度下降优化的外层结构,与是否向量化无关。 |
| 批次循环(Batch) | 无法消除 | Mini-batch 是训练策略的一部分,用于节省显存与稳定梯度,无法用矩阵运算替代。(一批次训练所有样本则不需此行) |
| 样本循环 | 被消除 | 向量化使得矩阵 ( \(X=[x^{(1)}, x^{(2)}, ...]\) ) 可以一次性处理所有样本,无需逐个 for。 |
| 层循环 | 无法消除 | 每层的输出依赖上一层结果,必须逐层计算,属于模型结构依赖,无法并行消除,只是代码中可不写显式 for。 |
| 层内神经元循环 | 被消除 | 矩阵乘法 ( \(Z = W A + b\) ) 可一次计算整层所有神经元的输出,无需逐神经元循环。 |
| 特征循环 | 被消除 | 神经元加权求和(点乘)由底层线性代数库以矩阵计算形式完成,无需手工遍历每个特征。 |
这里要单独说明一下层循环,层循环不同于轮次和批次,他不会直接使用显示的 for 语法。
层循环的本质是输入样本的处理顺序,我们只有在前一层得到结果后才可以进行下一层的计算,这样严密的串行结构无法并行消除 。
因此,我们才说习题里的说法是错误的。
1.3表格总结
| 循环类型 | 是否可向量化消除 |
|---|---|
| 轮次循环 | 不可消除 |
| 批次循环 | 不可消除 |
| 层循环 | 不可消除 |
| 样本循环 | 可消除 |
| 层内神经元循环 | 可消除 |
| 特征循环 | 可消除 |
2.代码实践:多层神经网络
吴恩达神经网络实战第四周同样先粘贴整理课程习题的博主答案,博主依旧在不借助很多现在流行框架的情况下手动构建 模型的各个部分,并手动实现传播,计算过程。
如果希望更扎实地了解原理,更推荐跟随这位博主的内容一步步手动构建模型,这样对之后框架的使用也会更得心应手。
这次实操不同于之前直接使用框架构建,我们在本周的理论部分里了解了正向传播和反向传播的模块化,再回看一下定义:
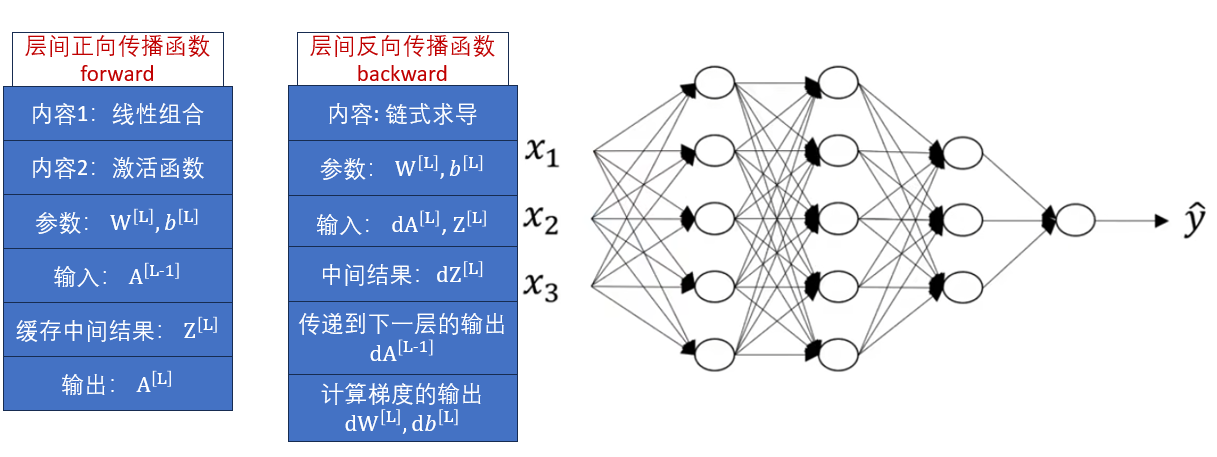
这次,我们按照理论梳理的内容,看看如何实现这两个函数 。
之后,再使用框架来看看多层神经网络对损失,对最终准确率的影响。
2.1 手工实现传播
1.正向传播
python
import numpy as np
# 1.定义ReLU激活函数用于隐藏层
def ReLU(Z):
return np.maximum(0, Z),Z # 返回格式:(层输出,加权和)
# 2.定义Sigmoid 激活函数用于输出层
def sigmoid(Z):
return 1/(1+np.exp(-Z)),Z # 返回格式:(层输出,加权和)
# 3.向前传播函数,实现线性组合+激活函数
def forward(A_prev, W, b, activation):
"""
参数介绍:
A_prev : 上一层输出 A^[L-1]
W : 当前层权重 W^[L]
b : 当前层偏置 b^[L]
activation : 本层使用的激活函数
"""
# 3.1 线性组合 Z = W*A_prev + b
Z = np.dot(W, A_prev) + b
# 3.2 激活函数
if activation == "sigmoid":
A, Z_cache = sigmoid(Z)
elif activation == "ReLU":
A, Z_cache = ReLU(Z)
else:
raise ValueError("未定义该激活函数")
# 3.3 保存中间值供 backward 使用
cache = (A_prev, W, b, Z_cache)
return A, cache
"""
返回:
A : 当前层输出 A^[L]
cache : 缓存中间结果 (A_prev, W, b, Z),用于反向传播
"""2.反向传播
python
import numpy as np
# 1. 激活函数的导数实现
def dReLU(dA, Z):
"""
ReLU 导数:
f(Z) = max(0, Z)
f'(Z) = 1, 若 Z > 0
0, 若 Z <= 0
"""
# dZ = dA*f'(Z)
dZ = np.array(dA, copy=True) # **确保修改dZ时不会影响到原始的dA
dZ[Z <= 0] = 0 # 只有 Z>0 时梯度能传递
return dZ
def dSigmoid(dA, Z):
"""
Sigmoid 导数:
A = σ(Z) = 1/(1 + e^-Z)
f'(Z) = A * (1 - A)
"""
A = 1 / (1 + np.exp(-Z))
# dZ = dA*f'(Z)
dZ = dA * A * (1 - A)
return dZ
# 2. 反向传播函数(链式求导得到参数梯度)
def backward(dA, cache, activation):
"""
参数:
dA : 当前层损失对激活输出 A^[L] 的梯度
cache : 前向传播保存的中间结果 (A_prev, W, b, Z)
activation : 本层使用的激活函数
"""
# 2.1取出前向传播缓存
A_prev, W, b, Z = cache
m = A_prev.shape[1] # 样本数量 m
# 2.2 根据激活函数计算 dZ
if activation == "ReLU":
dZ = dReLU(dA, Z)
elif activation == "sigmoid":
dZ = dSigmoid(dA, Z)
else:
raise ValueError("未定义的激活函数")
# 2.3 线性部分梯度(公式对应):
# dW = 1/m * dZ * A_prev^T
# db = 1/m * ∑(dZ)
# dA_prev = W^T * dZ
dW = (1/m) * np.dot(dZ, A_prev.T)
db = (1/m) * np.sum(dZ, axis=1, keepdims=True)
dA_prev = np.dot(W.T, dZ)
return dA_prev, dW, db
"""
返回:
dA_prev : 传递给上一层的梯度
dW : 当前层权重的梯度
db : 当前层偏置的梯度
"""这样,我们就实现了多层神经网络层间的正向传播和反向传播函数,如有更多兴趣可以去最开始推荐的博主的博客内,看看手工搭建整个神经网络的过程。
2.2 搭建多层神经网络
我们在第三周的代码实践中搭建的浅层神经网络的代码如下:
python
class ShallowNeuralNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten() #
# 隐藏层:输入128*128*3维特征,输出4个神经元
self.hidden = nn.Linear(128 * 128 * 3, 4)
# 隐藏层激活函数:ReLU,作用是加入非线性特征
self.ReLU = nn.ReLU()
# 输出层:将隐藏层的 4 个输出映射为 1 个加权和
self.output = nn.Linear(4, 1)
self.sigmoid = nn.Sigmoid()
# 前向传播方法
def forward(self, x):
# 输入 x 的维度为 [32, 3, 128, 128]
x = self.flatten(x)
# 展平后 x 的维度为 [32, 128 * 128 * 3]
x = self.hidden(x)
# 通过隐藏层线性变换后,x 的维度为 [32, 4]
x = self.ReLU(x)
# 经过 ReLU 激活后形状不变,仍为 [32, 4]
x = self.output(x)
# 通过输出层得到加权和,形状变为 [32, 1]
x = self.sigmoid(x)
# 经过 sigmoid 激活后得到 0~1 的概率值,形状仍为 [32, 1]
return x现在,我们再按本周理论内容里的多层神经网络修改一下,不改变其他部分:
经过三次代码实践 ,本周的内容里也总结了层级间维度变化的规律,想必对这部分的代码内容已经很熟悉了。这次就不再添加详细注释。
python
class ShallowNeuralNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
# 隐藏层
self.hidden1 = nn.Linear(128 * 128 * 3, 5)
self.hidden2 = nn.Linear(5, 5)
self.hidden3 = nn.Linear(5, 3)
self.ReLU = nn.ReLU()
# 输出层
self.output = nn.Linear(3, 1)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
x = self.flatten(x)
x = self.hidden1(x)
x = self.ReLU(x)
x = self.hidden2(x)
x = self.ReLU(x)
x = self.hidden3(x)
x = self.ReLU(x)
x = self.output(x)
x = self.sigmoid(x)
return x其构建的网络结构为:

很容易就可以对应出来。
2.3 结果分析
从浅层神经网络到多层神经网络,网络的规模再次扩大,带来的效果是什么样的呢?
我们还是先看结果:
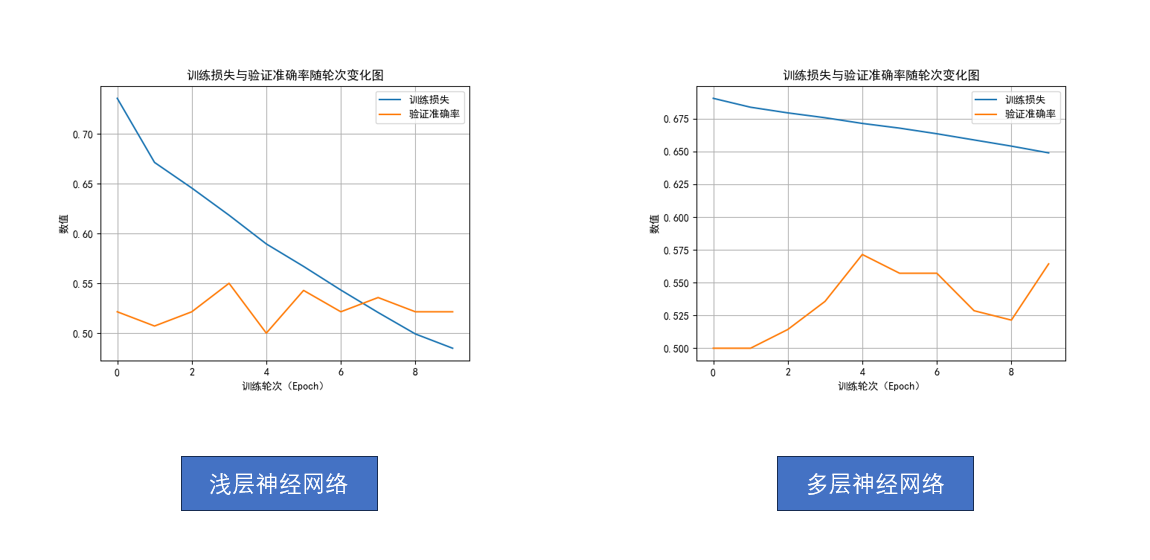
不对。
不是哥们,多了两层隐藏层,准确率没怎么升,损失收敛速度还变慢了?
先别急,回忆一下,在第三周,我们对比的是逻辑回归和浅层神经网络,从结果上我们得到的是浅层神经网络极大降低了损失。
当时为了控制变量,我们统一设置训练轮次 为10轮。
但有个容易忽略的前提------
当时的网络结构比较简单,10轮训练足够让它收敛 。
而现在我们提升到了多层神经网络,模型容量更大、表达的函数更复杂,再加上学习率设置得不高,仅仅训练10轮,根本不足以发挥出它的潜力 。
我们可以把它想象成:一场赛跑,浅层网络和多层网络都跑10圈,浅层网络更快,但它已经精疲力竭了,而后者刚刚结束热身。
为了让复杂的网络得到更充分的训练,现在我们把训练轮次增加到100轮 。
再次分别运行两个网络模型,来对比一下:
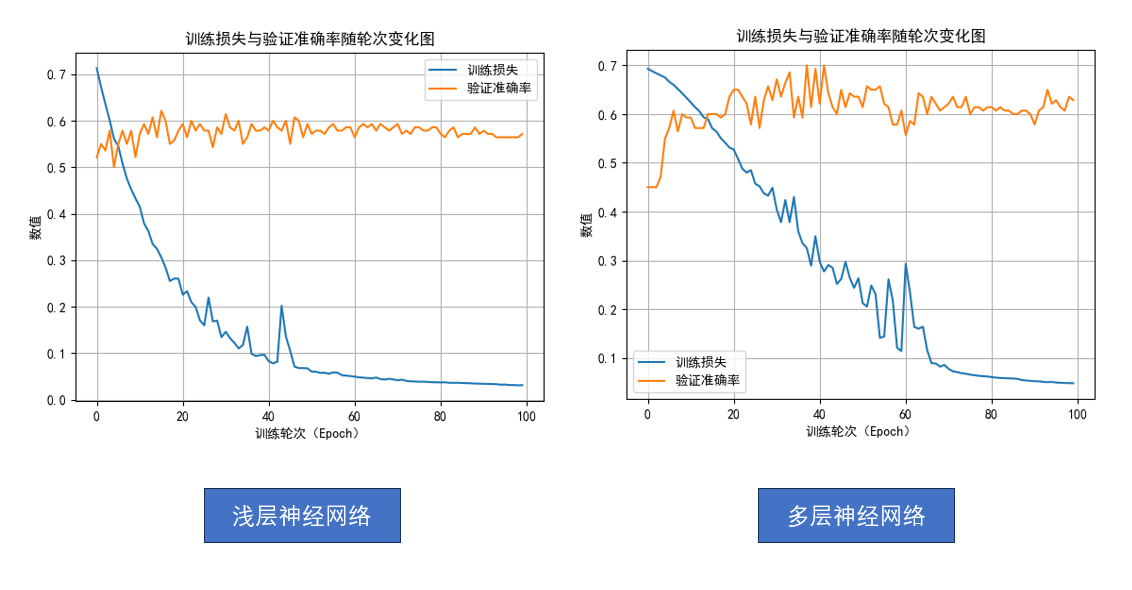
现在,是不是就能发现差别了?
- 浅层神经网络:即使训练到100轮,准确率依旧徘徊在 60% 左右,最高也难突破。
- 多层神经网络 :在大约第30轮后准确率迅速提升,最高甚至接近 70%,之后也很少跌回 60% 以下。
这就是我们之前提到的模型的"想象力"。
网络越深、参数越多,它越有能力去刻画复杂的函数关系,但反过来,它也需要更多时间和数据去学习,否则就像一位天赋很高但没受过训练的选手,潜力被埋没了。
这就是多层神经网络的效果。
3.总结
自此,吴恩达老师的深度学习第一课的笔记内容就结束了。
最后简单总结一下:
第一周,神经网络简洁,从概念上简单介绍了神经网络。
第二周,用逻辑回归这个单神经元网络讲解最简单的神经网络的传播过程。
第三周,从逻辑回归网络扩展到浅层神经网络,讲解隐藏层的作用和传播过程。
第四周,从浅层神经网络扩展到多层神经网络,补充更多细节和直观效果。
总的来说,第一课还是比较基础的内容。
之后的第二课开始就会以神经网络为基础,以实际网络运行中介绍其中的各种问题和解决方案,技术,会更加偏实践一些,也会更有"训练AI"的感觉。
最后附一下这次的多层神经网络完整代码:
python
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader, random_split
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score
transform = transforms.Compose([
transforms.Resize((128, 128)),
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))
])
dataset = datasets.ImageFolder(root='./cat_dog', transform=transform)
train_size = int(0.8 * len(dataset))
val_size = int(0.1 * len(dataset))
test_size = len(dataset) - train_size - val_size
train_dataset, val_dataset, test_dataset = random_split(dataset, [train_size, val_size, test_size])
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)
val_loader = DataLoader(val_dataset, batch_size=32, shuffle=False)
test_loader = DataLoader(test_dataset, batch_size=32, shuffle=False)
class ShallowNeuralNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
# 隐藏层
self.hidden1 = nn.Linear(128 * 128 * 3, 5)
self.hidden2 = nn.Linear(5, 5)
self.hidden3 = nn.Linear(5, 3)
self.ReLU = nn.ReLU()
# 输出层
self.output = nn.Linear(3, 1)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
x = self.flatten(x)
x = self.hidden1(x)
x = self.ReLU(x)
x = self.hidden2(x)
x = self.ReLU(x)
x = self.hidden3(x)
x = self.ReLU(x)
x = self.output(x)
x = self.sigmoid(x)
return x
model = ShallowNeuralNetwork()
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model.to(device)
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)
epochs =10
train_losses = []
val_accuracies = []
for epoch in range(epochs):
model.train()
epoch_train_loss = 0
for images, labels in train_loader:
images, labels = images.to(device), labels.to(device).float().unsqueeze(1)
outputs = model(images)
loss = criterion(outputs, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
epoch_train_loss += loss.item()
avg_train_loss = epoch_train_loss / len(train_loader)
train_losses.append(avg_train_loss)
model.eval()
val_true, val_pred = [], []
with torch.no_grad():
for images, labels in val_loader:
images = images.to(device)
outputs = model(images)
preds = (outputs.cpu().numpy() > 0.5).astype(int).flatten()
val_pred.extend(preds)
val_true.extend(labels.numpy())
val_acc = accuracy_score(val_true, val_pred)
val_accuracies.append(val_acc)
print(f"轮次: [{epoch + 1}/{epochs}], 训练损失: {avg_train_loss:.4f}, 验证准确率: {val_acc:.4f}")
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.plot(train_losses, label='训练损失')
plt.plot(val_accuracies, label='验证准确率')
plt.title("训练损失与验证准确率随轮次变化图")
plt.xlabel("训练轮次(Epoch)")
plt.ylabel("数值")
plt.legend()
plt.grid(True)
plt.show()
model.eval()
y_true, y_pred = [], []
with torch.no_grad():
for images, labels in test_loader:
images = images.to(device)
outputs = model(images)
preds = (outputs.cpu().numpy() > 0.5).astype(int).flatten()
y_pred.extend(preds)
y_true.extend(labels.numpy())
acc = accuracy_score(y_true, y_pred)
print(f"测试准确率: {acc:.4f}")