文章目录
- [一 调试学习算法的挑战](#一 调试学习算法的挑战)
- [二 机器学习诊断法](#二 机器学习诊断法)
- [三 评估你的模型](#三 评估你的模型)
-
- [3.1 过拟合问题与数据集划分](#3.1 过拟合问题与数据集划分)
- [3.2 线性回归的训练与测试流程](#3.2 线性回归的训练与测试流程)
- [3.3 分类问题的训练与测试流程](#3.3 分类问题的训练与测试流程)
- [四 模型选择问题](#四 模型选择问题)
-
- [4.1 测试集的局限性](#4.1 测试集的局限性)
- [4.2 引入交叉验证集](#4.2 引入交叉验证集)
- [4.3 正确的模型选择流程](#4.3 正确的模型选择流程)
- [五 诊断偏差与方差](#五 诊断偏差与方差)
-
- [5.1 理解偏差与方差](#5.1 理解偏差与方差)
- [5.2 如何判断是偏差还是方差问题](#5.2 如何判断是偏差还是方差问题)
- [六 正则化与偏差/方差的关系](#六 正则化与偏差/方差的关系)
- [七 基准性能与学习曲线](#七 基准性能与学习曲线)
-
- [7.1 建立性能基准](#7.1 建立性能基准)
- [7.2 学习曲线](#7.2 学习曲线)
视频链接
吴恩达机器学习p70-76
一 调试学习算法的挑战
在机器学习的实践中,我们经常会遇到这样的情况:我们已经实现了一个模型,比如带有正则化的线性回归模型来预测房价,但它在预测新数据时却出现了无法接受的巨大误差。

面对这种情况,我们应该怎么办呢?我们有很多可以尝试的策略:
- 获取更多的训练样本
- 尝试使用更少的特征
- 尝试获取更多的特征
- 尝试添加多项式特征 (如 x₁², x₁x₂, etc)
- 尝试减小正则化参数 λ
- 尝试增大正则化参数 λ
这些方法看起来都有道理,但问题在于,我们应该选择哪一个?随意选择一个方向进行尝试可能会花费我们数周甚至数月的时间,但最终可能收效甚微。因此,我们需要一种更系统、更有效的方法来指导我们优化算法。
二 机器学习诊断法
为了解决上述问题,吴恩达老师引入了"机器学习诊断法"(Machine learning diagnostic)的概念。

所谓诊断法,它本身就是一种测试。通过运行这些测试,我们可以深入洞察一个学习算法的有效之处和无效之处,从而为我们改进算法性能提供明确的指导。
虽然实现这些诊断法本身可能需要花费一些时间,但这样做是非常值得的,因为它能有效避免我们把大量时间浪费在错误的方向上,从而大大提高我们优化模型的效率。
三 评估你的模型
3.1 过拟合问题与数据集划分
在评估模型时,我们首先要面对的问题就是"过拟合"(Overfitting)。如下图所示,一个模型可能对训练数据拟合得非常好(图中蓝线穿过了所有的红色训练样本点),但它却无法很好地泛化到训练集之外的新样本上。这种模型的泛化能力很差。

为了能够客观地评估模型的泛化能力,我们需要将我们的数据集进行划分。一个常见的做法是将数据分为"训练集"(training set)和"测试集"(test set)。

如图所示,我们可以按照一定的比例,比如70%的数据作为训练集,用于训练模型的参数 w 和 b;剩下的30%作为测试集,用于评估训练好的模型的性能。
3.2 线性回归的训练与测试流程
对于带有平方误差代价的线性回归问题,其评估流程如下:

- 参数拟合 :使用训练集的数据,通过最小化代价函数 J(w,b) 来找到最优的参数 w 和 b。注意,这里的代价函数是包含正则化项的。
- 计算测试误差 :使用训练好的参数 w 和 b,在测试集上计算模型的误差,记为 J_test。测试误差反映了模型对新样本的泛化能力。
- 计算训练误差 :同样使用训练好的参数 w 和 b,在训练集上计算模型的误差,记为 J_train。
注意:在计算测试集误差 J_test 时,通常我们只关心模型在新数据上的预测表现,因此标准的做法是使用不含正则化项的代价函数。上图幻灯片中将正则化项放在了 J_test 的公式中,这是一种不太常规的表示,但在本课程的语境下,我们遵循讲师的定义。核心思想是使用一份"干净"的、未参与训练的数据来评估模型。

对于一个过拟合的模型,我们通常会观察到:
- J_train 会很低:因为模型几乎完美地拟合了训练数据。
- J_test 会很高:因为模型没能学到数据的一般规律,在新的测试数据上表现很差。
3.3 分类问题的训练与测试流程
同样的方法也适用于分类问题,例如逻辑回归。

- 参数拟合 :使用训练集,通过最小化逻辑回归的代价函数(带有正则化项)来找到最优参数 w 和 b。
- 计算测试误差 :在测试集上计算代价函数的值 J_test。
- 计算训练误差 :在训练集上计算代价函数的值 J_train。
与回归问题类似,计算测试误差和训练误差时,我们通常使用不含正则化项的代价函数,以反映模型本身的预测性能。

对于分类问题,除了使用代价函数作为误差度量外,我们还可以使用一种更直观的度量方法:误分类率(misclassification error)。
- J_test(w,b) = 测试集中被模型错误分类的样本比例。
- J_train(w,b) = 训练集中被模型错误分类的样本比例。
这种0/1误差度量方式简单明了,更容易解释。
四 模型选择问题
在实际应用中,我们往往需要从多个模型中选择一个最优的。这个过程就叫做"模型选择"(Model selection)。
4.1 测试集的局限性

我们知道,训练误差 J_train 通常会比模型的真实泛化误差要低,因为它是在模型"见过"的数据上计算的。相比之下,测试误差 J_test 是对模型泛化能力的一个更好的估计。

假设我们现在要选择一个多项式回归模型的最佳次数 d。我们可以构建10个不同的模型,d 从1到10。一个很自然的想法是:
- 用训练集训练这10个模型。
- 用测试集分别评估这10个模型,计算出10个 J_test。
- 选择那个 J_test 最小的模型,比如
d=5的模型。
但这里有一个严重的问题 :我们用测试集来选择了模型的超参数 d。这意味着,我们得到的这个 J_test(w<5>, b<5>) 很可能是对泛化误差的一个过于乐观的估计 。因为我们已经让模型为了在测试集上表现更好而调整了超参数 d,测试集在某种程度上已经"泄露"给了模型选择过程。这样得到的模型,在遇到全新的、真正未知的数据时,表现可能并不会像这个 J_test 显示的那么好。
4.2 引入交叉验证集
为了解决上述问题,我们需要引入第三个数据集:"交叉验证集"(Cross validation set),有时也称为"开发集"(development set, dev set)。
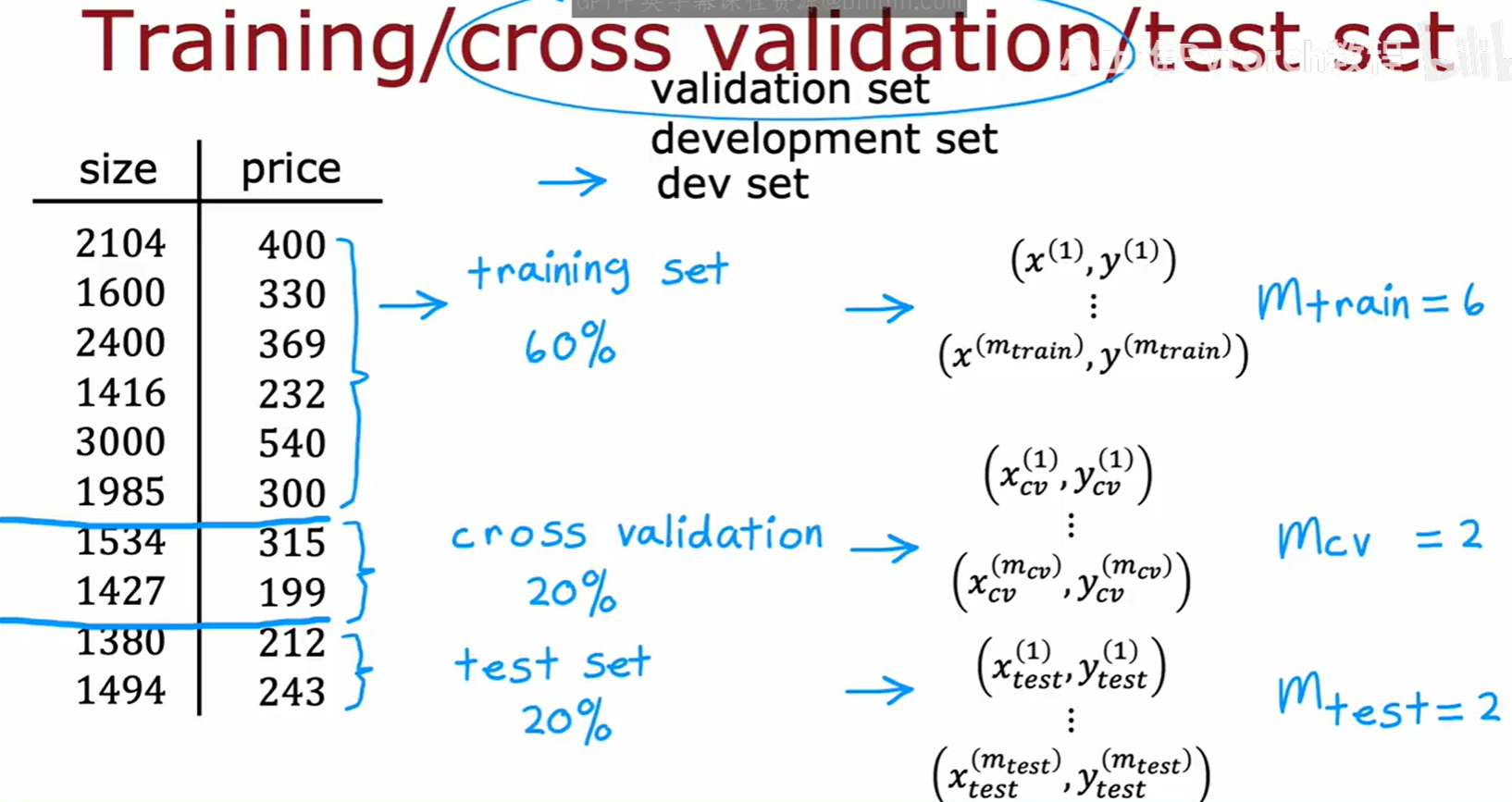
现在,我们将整个数据集划分为三部分:
- 训练集 (Training set):例如60%的数据,用于训练模型的参数 w, b。
- 交叉验证集 (Cross validation set) :例如20%的数据,用于模型选择(如选择多项式次数
d或正则化参数λ)。 - 测试集 (Test set):例如20%的数据,用于在模型选择完成后,对最终选定的模型进行一次性的、最终的性能评估。

相应地,我们现在有三个误差指标:
- 训练误差 J_train:在训练集上计算。
- 交叉验证误差 J_cv:在交叉验证集上计算。
- 测试误差 J_test:在测试集上计算。
4.3 正确的模型选择流程
有了这三个数据集,正确的模型选择和评估流程应该是这样的:

- 使用训练集训练所有候选模型(例如,d=1 到 d=10 的多项式模型)。
- 使用交叉验证集评估所有这些模型,计算 J_cv。
- 选择 J_cv 最小的那个模型作为我们的最终模型(例如,上图中
d=4的模型)。 - 最后,为了得到对最终模型泛化能力的无偏估计,我们使用测试集来计算 J_test。这个 J_test 值将作为我们对外报告的模型性能指标。
核心思想是:测试集绝对不能参与任何训练或模型选择的过程,它只能在所有工作都完成之后,像"期末考试"一样,被用来评估最终模型的泛化能力。
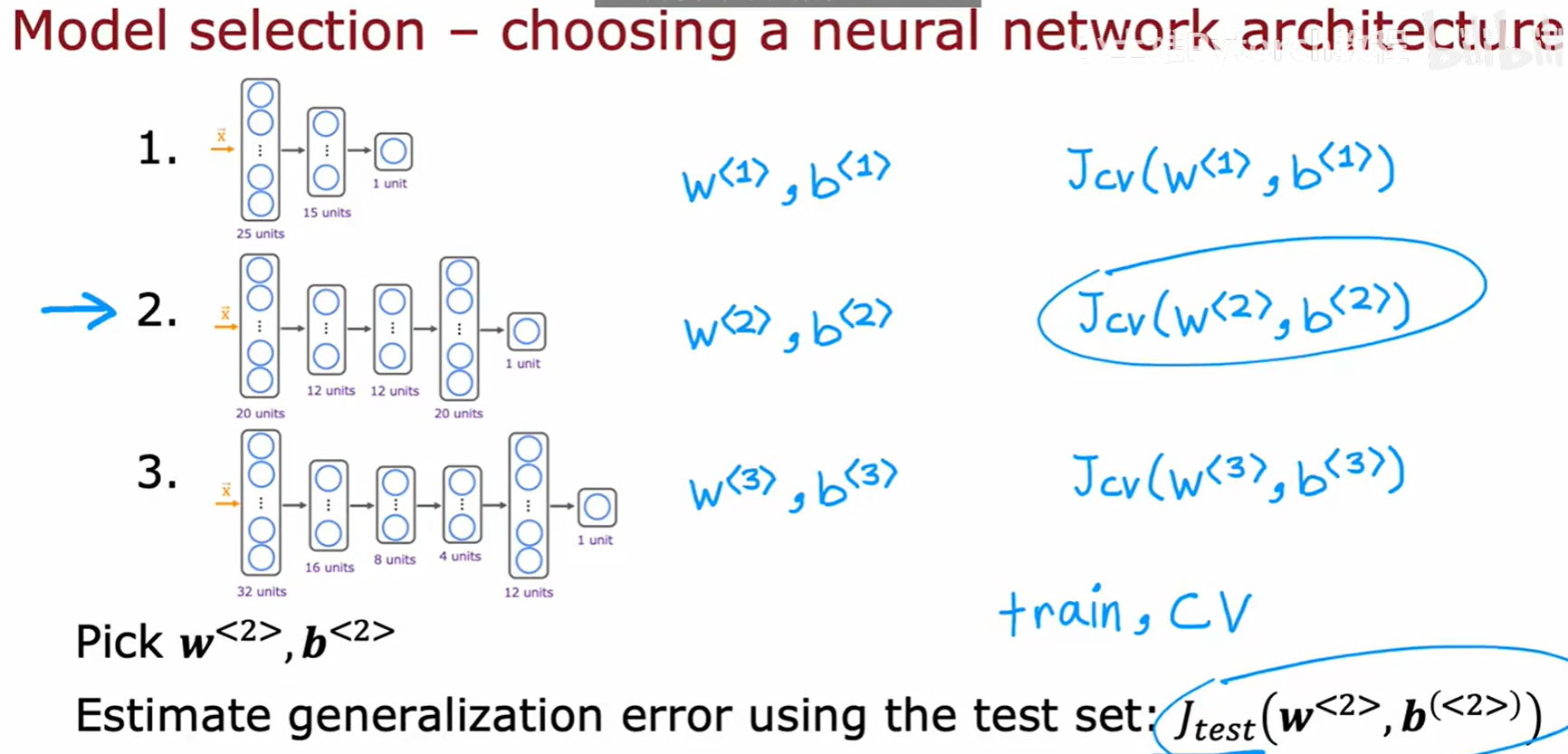
这个流程同样适用于选择神经网络的结构。我们可以设计多种不同的网络结构(不同的层数、不同的单元数),用训练集训练它们,用交叉验证集选出表现最好的那个结构,最后用测试集来评估它的最终性能。
五 诊断偏差与方差
现在,我们回到最初的问题:如何系统地判断模型出了什么问题?偏差(Bias)和方差(Variance)是两个核心的诊断工具。
5.1 理解偏差与方差
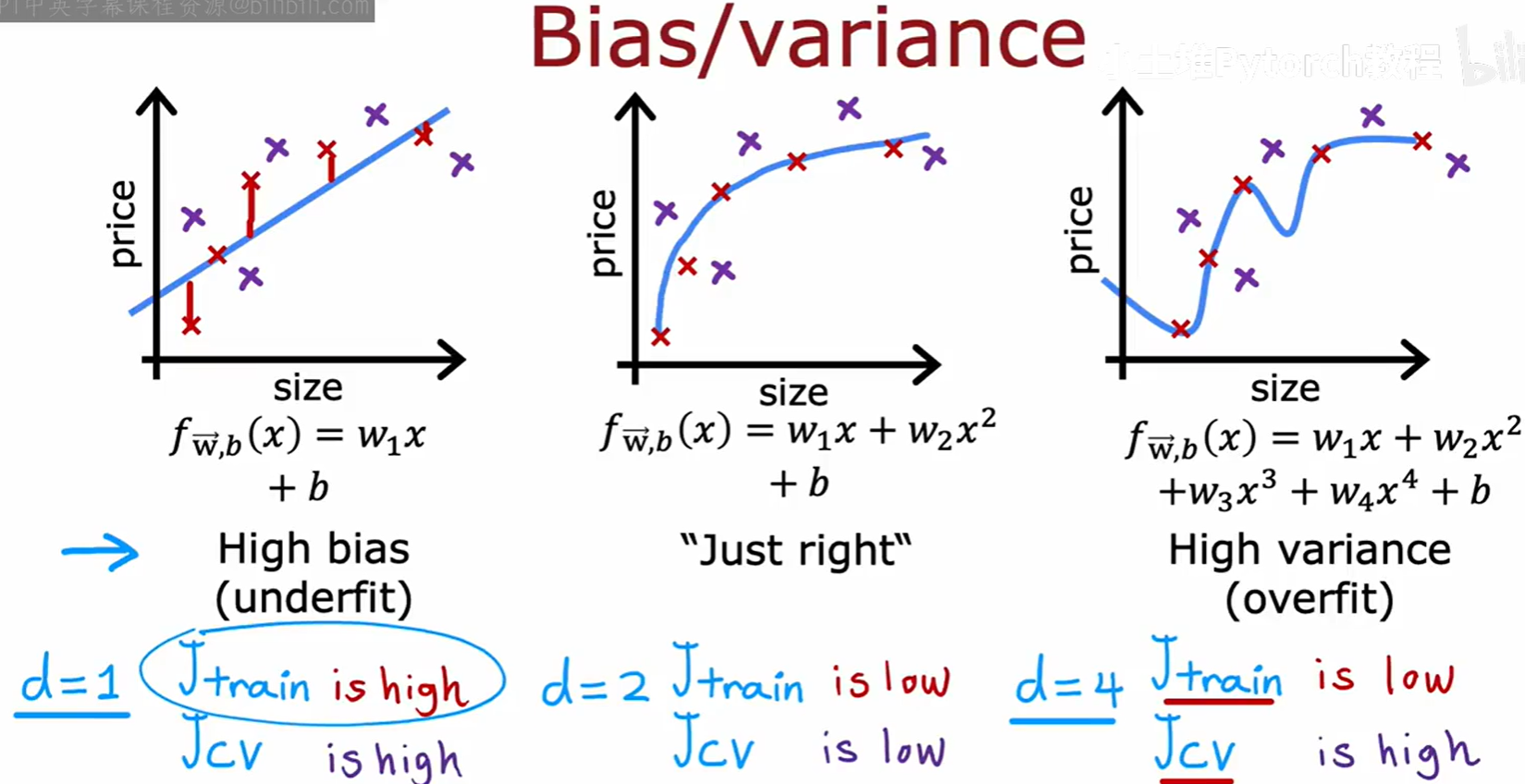
- 高偏差 (High bias) :也称作"欠拟合"(Underfit)。模型过于简单,无法捕捉数据中的基本规律。例如,用一条直线去拟合非线性的数据。
- 表现:训练误差 J_train 会很高,同时交叉验证误差 J_cv 也会很高。
- 高方差 (High variance) :也称作"过拟合"(Overfit)。模型过于复杂,过度拟合了训练数据中的噪声和细节,导致其泛化能力很差。
- 表现:训练误差 J_train 会很低,但交叉验证误差 J_cv 会很高。
- "刚刚好" (Just right) :模型复杂程度适中,很好地平衡了偏差和方差。
- 表现:训练误差 J_train 会很低,同时交叉验证误差 J_cv 也会很低。
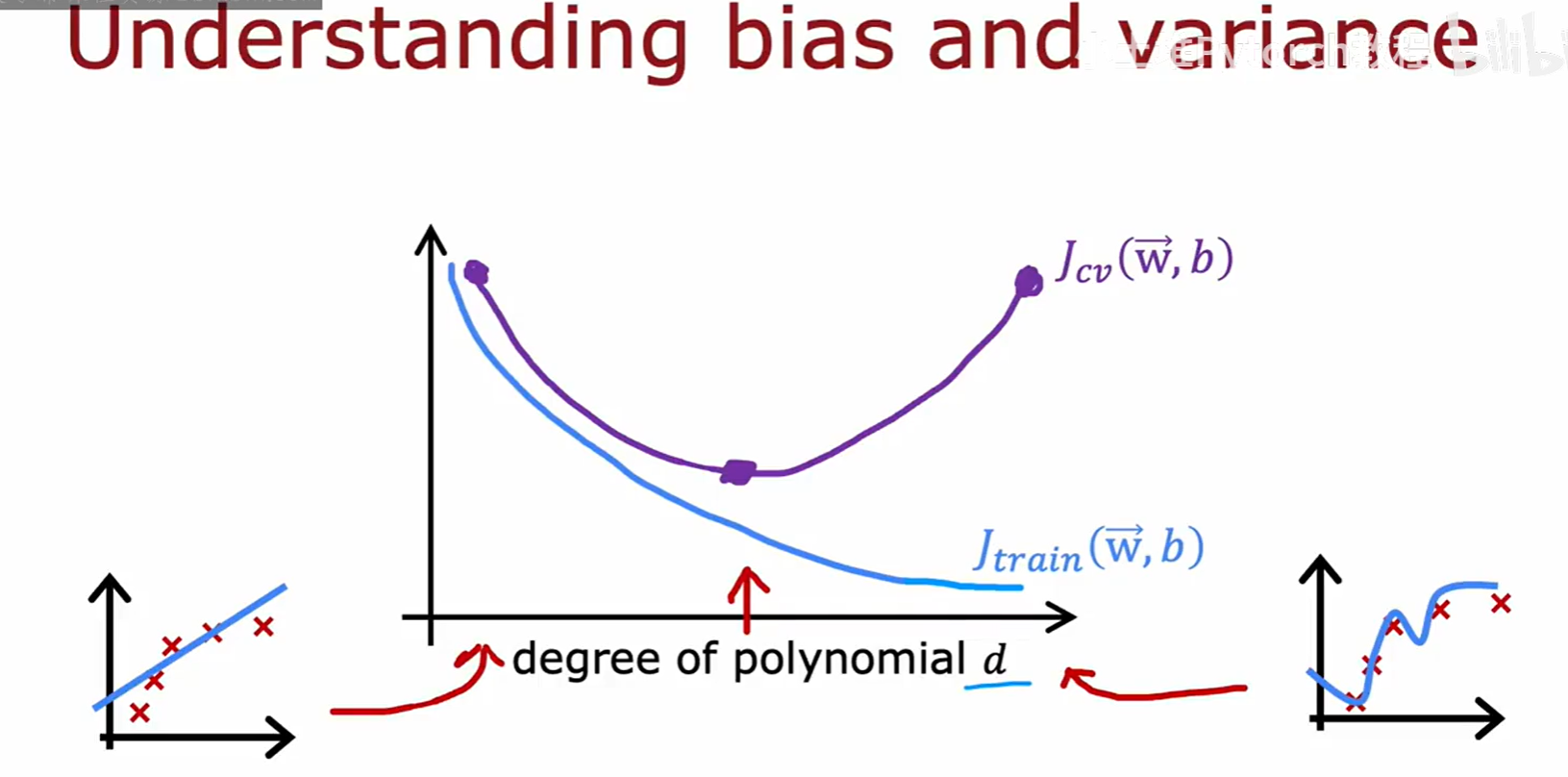
我们可以通过绘制 J_train 和 J_cv 随模型复杂度(例如多项式次数 d)变化的曲线来直观地理解这一点。
- 随着
d增大,J_train 倾向于单调递减。 - J_cv 则会先减小(因为模型拟合能力增强),然后增大(因为模型开始过拟合)。
- 我们的目标是找到那个使 J_cv 最小化的复杂度
d。
5.2 如何判断是偏差还是方差问题

根据 J_train 和 J_cv 的值,我们可以做出如下诊断:
- 高偏差问题:如果 J_train 本身就很高,并且 J_cv 与 J_train 的值很接近(J_cv ≈ J_train),这说明模型连训练数据都拟合不好,是欠拟合了。
- 高方差问题:如果 J_train 很低,但 J_cv 远大于 J_train(J_cv >> J_train),这说明模型在训练集上表现很好,但在验证集上表现很差,是过拟合了。
- 高偏差且高方差问题:如果 J_train 很高,并且 J_cv 比 J_train 还要高很多(J_cv >> J_train),这说明模型既有欠拟合的问题,又有过拟合的问题。
六 正则化与偏差/方差的关系
正则化是控制模型复杂度,从而调节偏差和方差的有效工具。
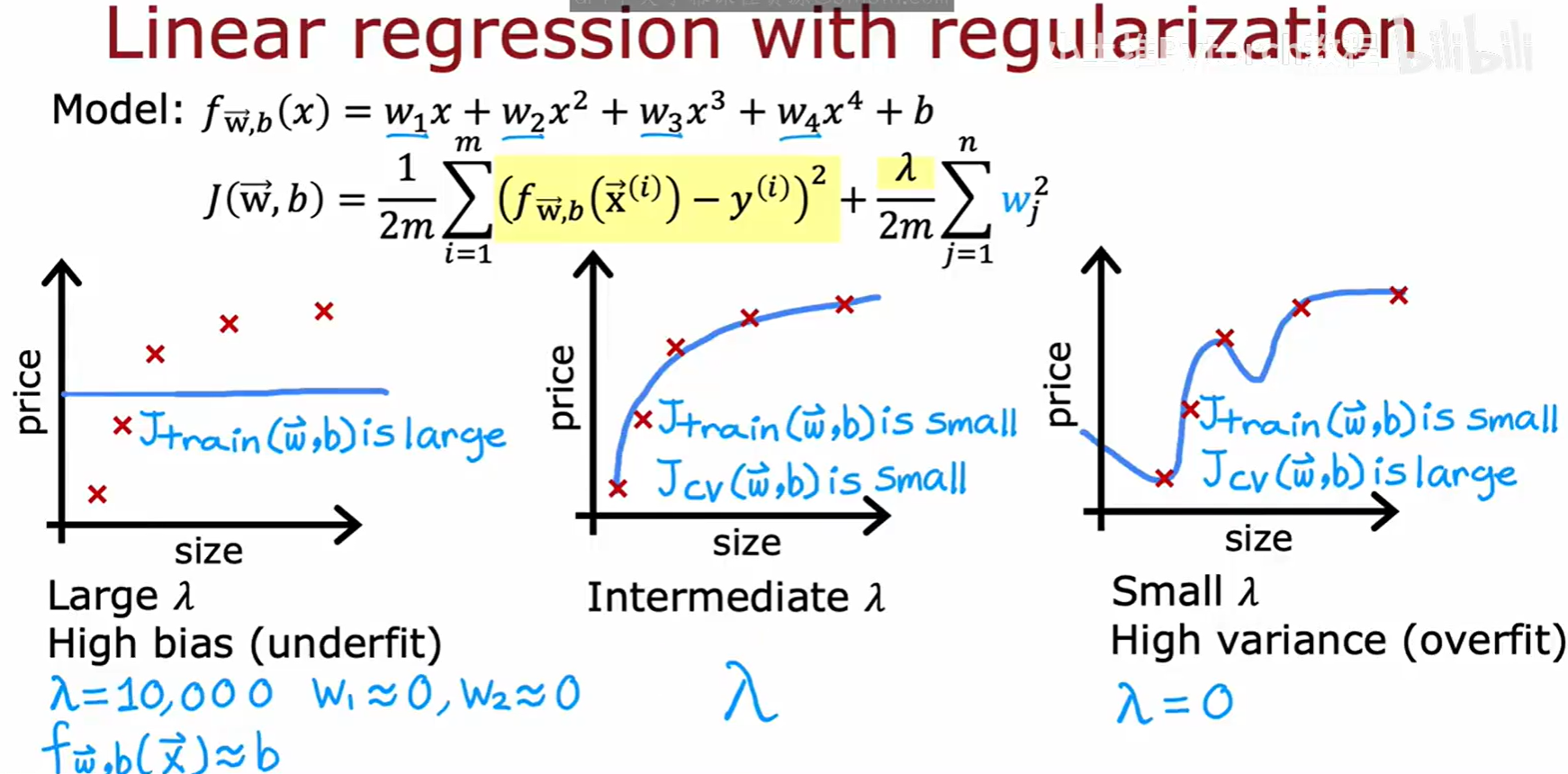
我们通过调整正则化参数 λ 来控制模型的偏差-方差平衡:
- 大的 λ :对参数 w 的惩罚很重,会使参数趋近于0,导致模型非常简单(例如近似一条水平线),从而产生高偏差(欠拟合)。此时 J_train 和 J_cv 都会很大。
- 小的 λ (例如 λ=0):对参数 w 几乎没有惩罚,允许模型变得非常复杂以拟合所有训练数据,从而导致高方差(过拟合)。此时 J_train 会很小,但 J_cv 会很大。
- 适中的 λ:能在两者之间找到一个很好的平衡,使得 J_train 和 J_cv 都比较小。

选择最佳 λ 的过程与选择多项式次数 d 的过程完全一样,是一个典型的模型选择问题:
- 选取一系列
λ的候选值(例如 0, 0.01, 0.02, ..., 10)。 - 对于每一个
λ,使用训练集训练模型得到对应的参数 w, b。 - 在交叉验证集上评估每一个模型,计算 J_cv。
- 选择使 J_cv 最小的那个
λ作为最终参数。 - 最后,使用测试集评估最终选定模型的性能。
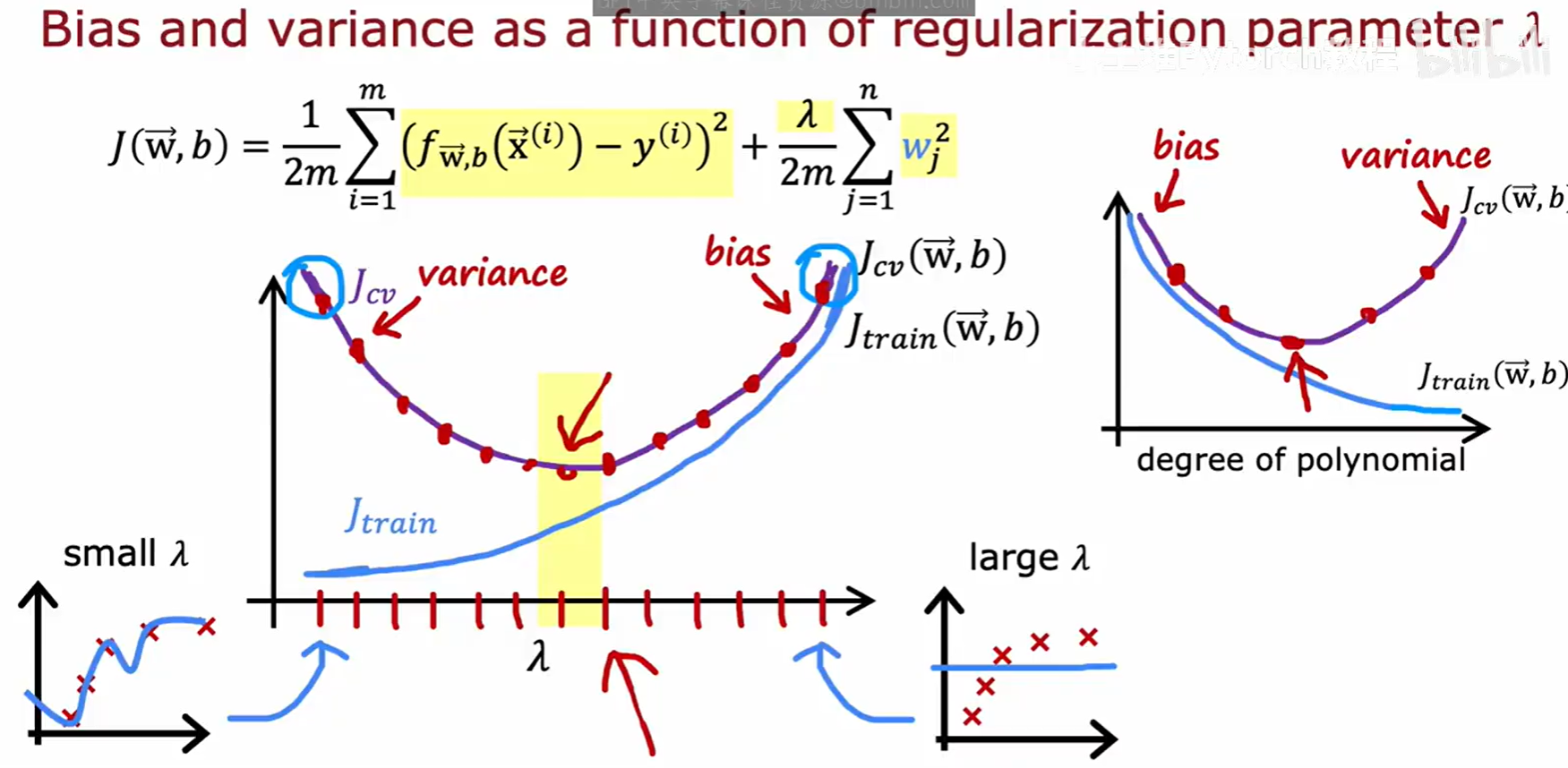
我们可以绘制 J_train 和 J_cv 随 λ 变化的曲线。随着 λ 从小到大变化,模型从高方差区域(左侧)过渡到高偏差区域(右侧)。我们的目标是找到 J_cv 曲线的最低点对应的 λ 值。
七 基准性能与学习曲线
7.1 建立性能基准
为了判断我们的误差(例如10.8%)到底算高还是算低,我们需要一个参考标准,即性能基准(Baseline level of performance)。
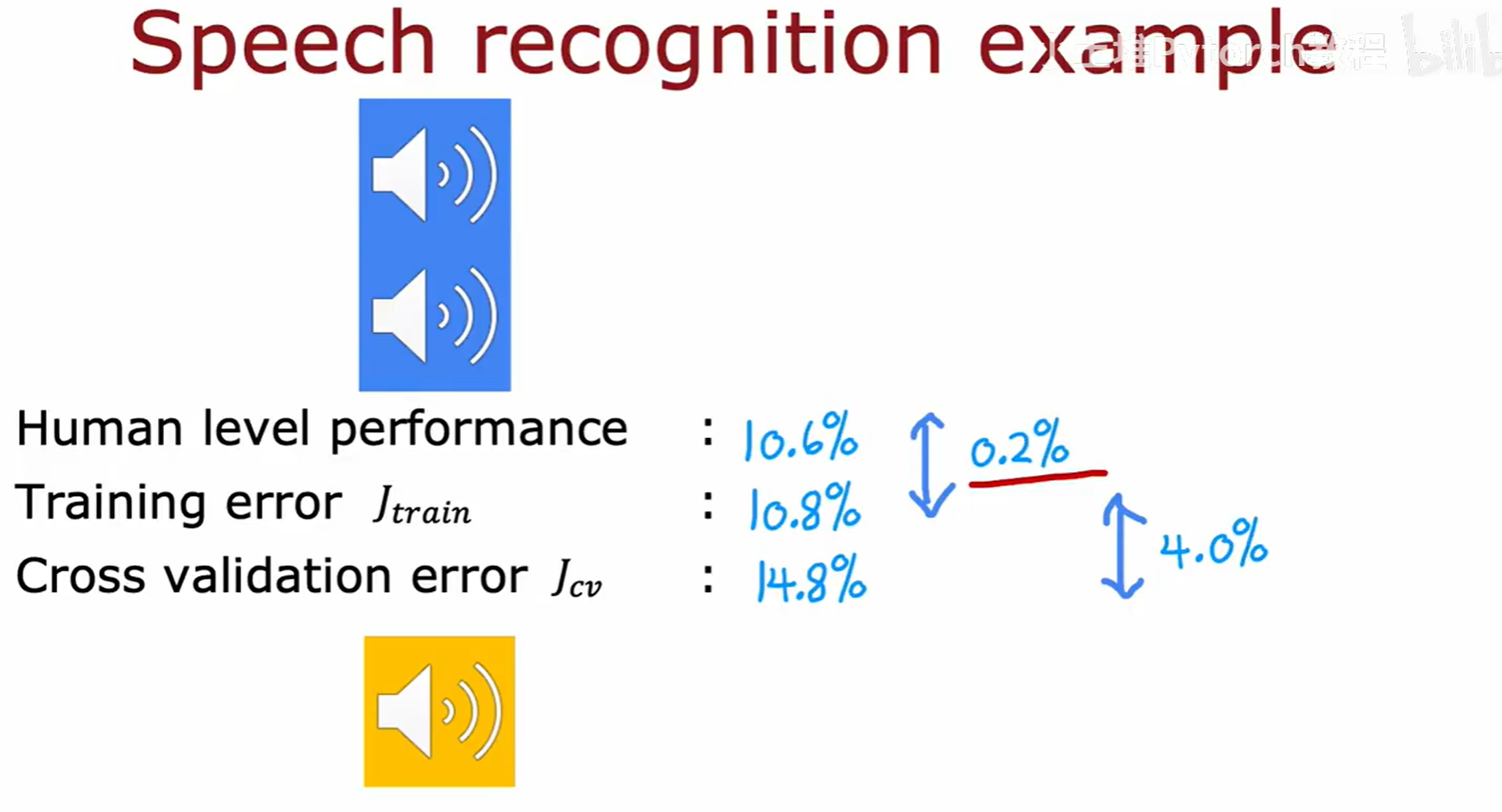
例如,在语音识别任务中,如果人类的错误率(Human level performance)是10.6%,而我们的模型训练误差是10.8%,交叉验证误差是14.8%。
- 可避免的偏差 (Avoidable bias):训练误差与基准性能的差距 (10.8% - 10.6% = 0.2%)。这个差距很小,说明模型的偏差问题不大。
- 方差 (Variance):交叉验证误差与训练误差的差距 (14.8% - 10.8% = 4.0%)。这个差距很大,说明模型的主要问题是方差太高(过拟合)。

如何确定基准性能?可以参考:
- 人类在该任务上的表现水平。
- 其他现有算法的性能。
- 根据经验进行的合理猜测。

通过比较训练误差、交叉验证误差和基准性能,我们可以更精确地诊断问题所在:
- 例1(高方差):可避免偏差小 (0.2%),方差大 (4.0%)。主要矛盾是过拟合。
- 例2(高偏差):可避免偏差大 (4.4%),方差小 (0.5%)。主要矛盾是欠拟合。
- 例3(高偏差和高方差):可避免偏差大 (4.4%),方差也大 (4.7%)。两者都是问题。
7.2 学习曲线
学习曲线(Learning curves)是另一种强大的诊断工具。它描绘了模型的训练误差和交叉验证误差随着训练样本数量 m_train 变化的趋势。
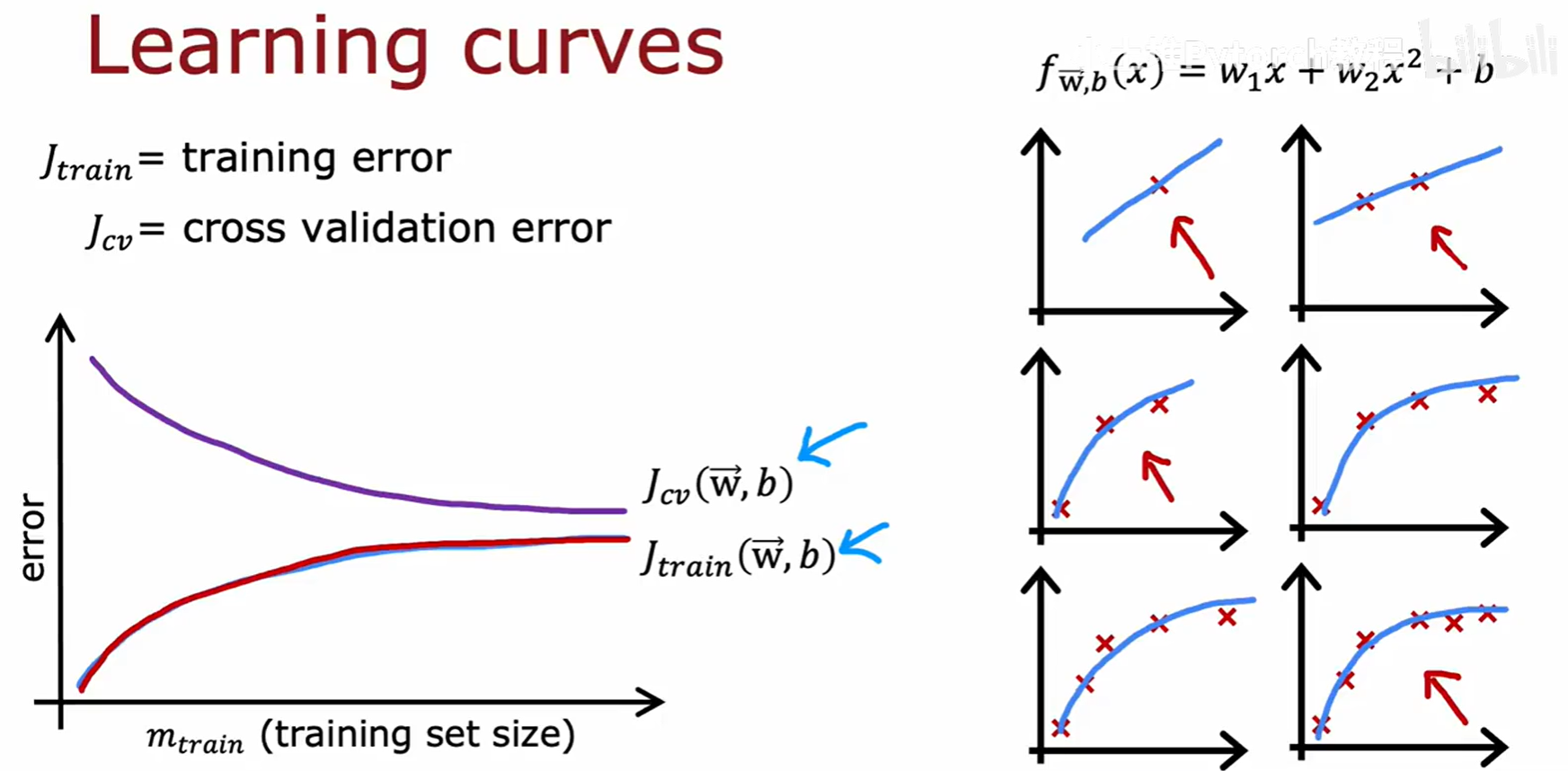
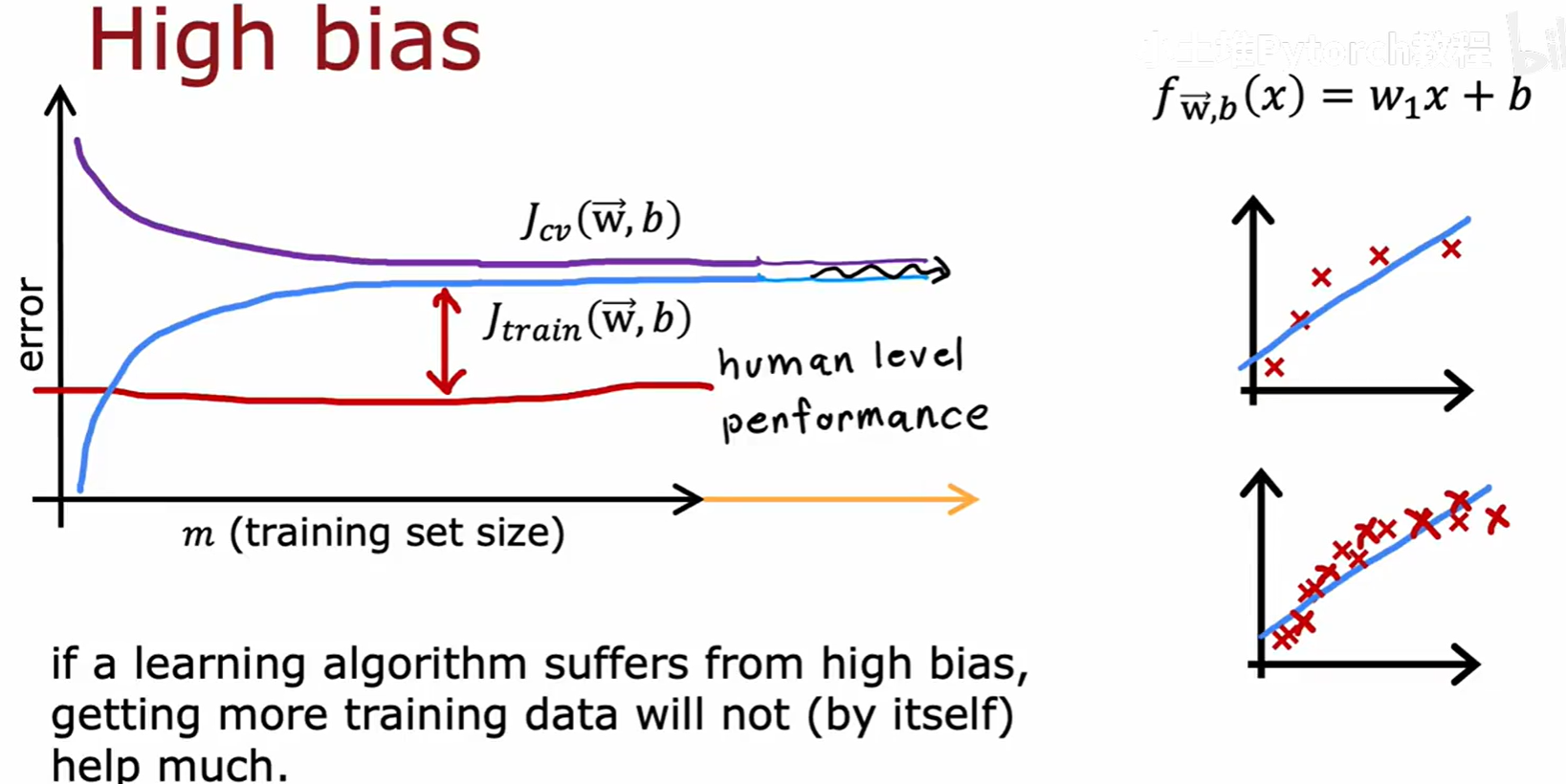
高偏差(欠拟合)模型的学习曲线特征:
- 随着训练样本增多,J_train 逐渐升高(因为模型越来越难拟合所有数据),J_cv 逐渐降低。
- 最终,J_train 和 J_cv 会收敛到一起,并且都处于一个较高的水平。
- 结论 :如果一个算法存在高偏差问题,那么增加更多的训练数据是徒劳的,因为曲线已经趋于平坦,增加数据并不会显著降低误差。
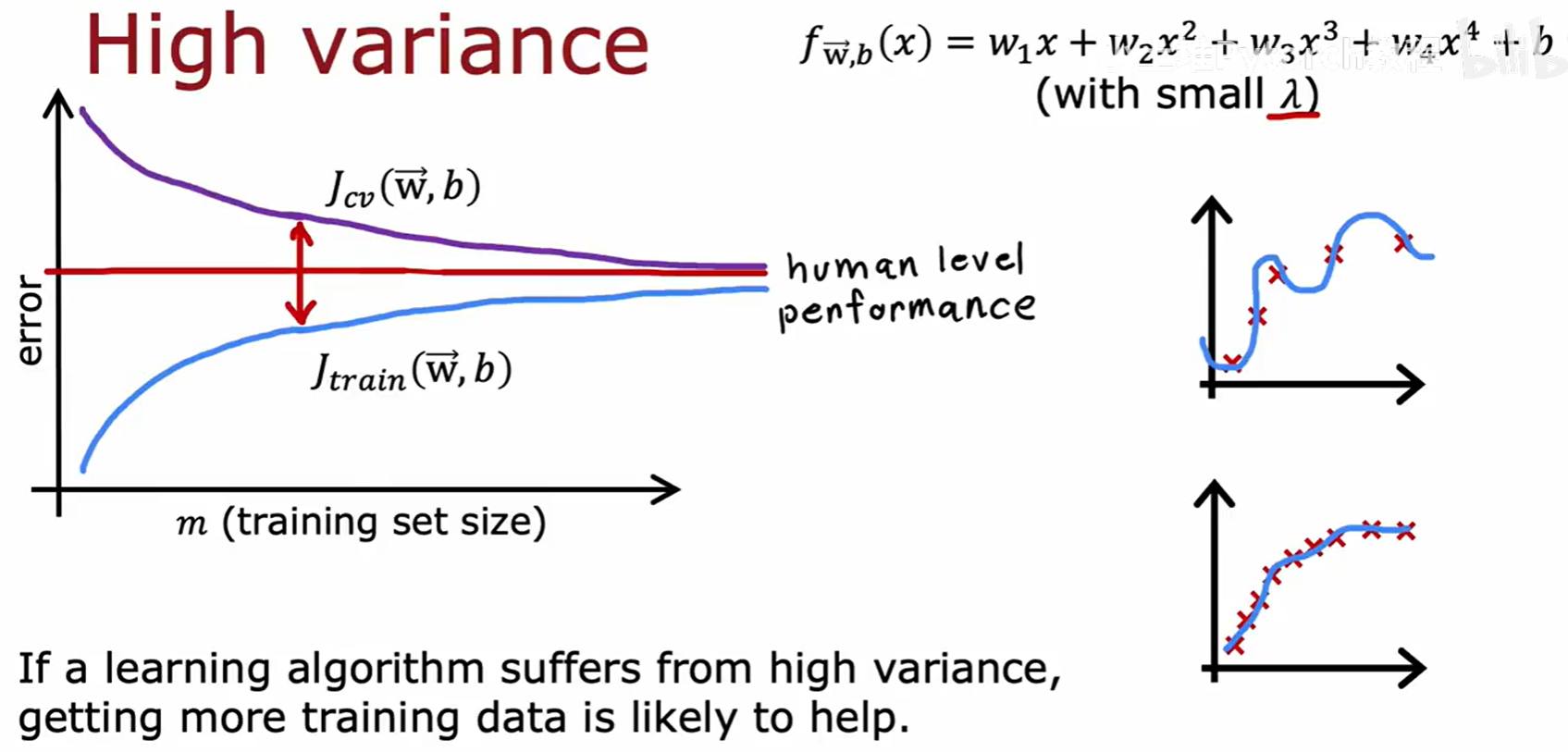
高方差(过拟合)模型的学习曲线特征:
- J_train 始终处于一个很低的水平。
- J_cv 则远高于 J_train,两者之间存在一个巨大的差距(gap)。
- 随着训练样本增多,J_train 会缓慢上升,而 J_cv 会显著下降,两者之间的差距会减小。
- 结论 :如果一个算法存在高方差问题,那么增加更多的训练数据是很有可能帮助改善模型性能的,因为这会帮助模型学到更普适的规律,减小过拟合。
通过上述的诊断法、模型选择流程以及偏差/方差分析工具,我们就能回到文章开头的那个问题,不再是盲目尝试,而是可以根据模型的具体"症状","对症下药"地选择最有效的优化策略。