导数和微分是微积分的核心概念,它们描述了函数变化的"速度"和"局部线性近似"。本文通过几何直观和Python案例,带你深入理解这两个重要概念!
一、导数与微分的历史背景
导数和微分是一元函数微分学中两个重要且密切相关的概念,在科学和工程技术中有极为广泛的应用。从17世纪开始,随着近代航海业和工业的发展,数学家们逐渐建立了这些概念。
历史小知识:牛顿和莱布尼茨独立发展了微积分,为解决天体运动、物体运动等实际问题提供了数学工具。
二、为什么需要导数?------实际问题驱动
1. 连续性的局限
前面学习的函数在一点连续的性质,反映的是函数值 f(x)f(x)f(x) 在一点附近随着自变量的变化而变化的定性性质 。但实际问题中,我们更需要定量描述变化的速度!
2. 三个经典问题
🔍 问题1:曲线的斜率(几何问题)
当 (x0,y0)(x_0, y_0)(x0,y0) 与 (x,y)(x, y)(x,y) 是直线 LLL 上的两点时,比值 y−y0x−x0\frac{y - y_0}{x - x_0}x−x0y−y0 表示直线 LLL 的斜率。
Python可视化:直线斜率计算
python
import matplotlib.pyplot as plt
import numpy as np
# 中文显示
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
def demonstrate_slope():
"""演示直线斜率的几何意义"""
x0, y0 = 1, 2 # 起点
x1, y1 = 4, 5 # 终点
# 计算斜率
slope = (y1 - y0) / (x1 - x0)
plt.figure(figsize=(8, 6))
plt.plot([x0, x1], [y0, y1], 'b-', linewidth=2, label=f'直线L, 斜率k={slope}')
plt.scatter([x0, x1], [y0, y1], color='red', s=100)
# 标注坐标
plt.annotate(f'({x0}, {y0})', (x0, y0), xytext=(x0-0.1, y0+0.1))
plt.annotate(f'({x1}, {y1})', (x1, y1), xytext=(x1+0.2, y1))
plt.title('直线斜率的几何意义')
plt.xlabel('x'); plt.ylabel('y')
plt.grid(True, alpha=0.3)
plt.legend()
plt.axis('equal')
plt.show()
demonstrate_slope()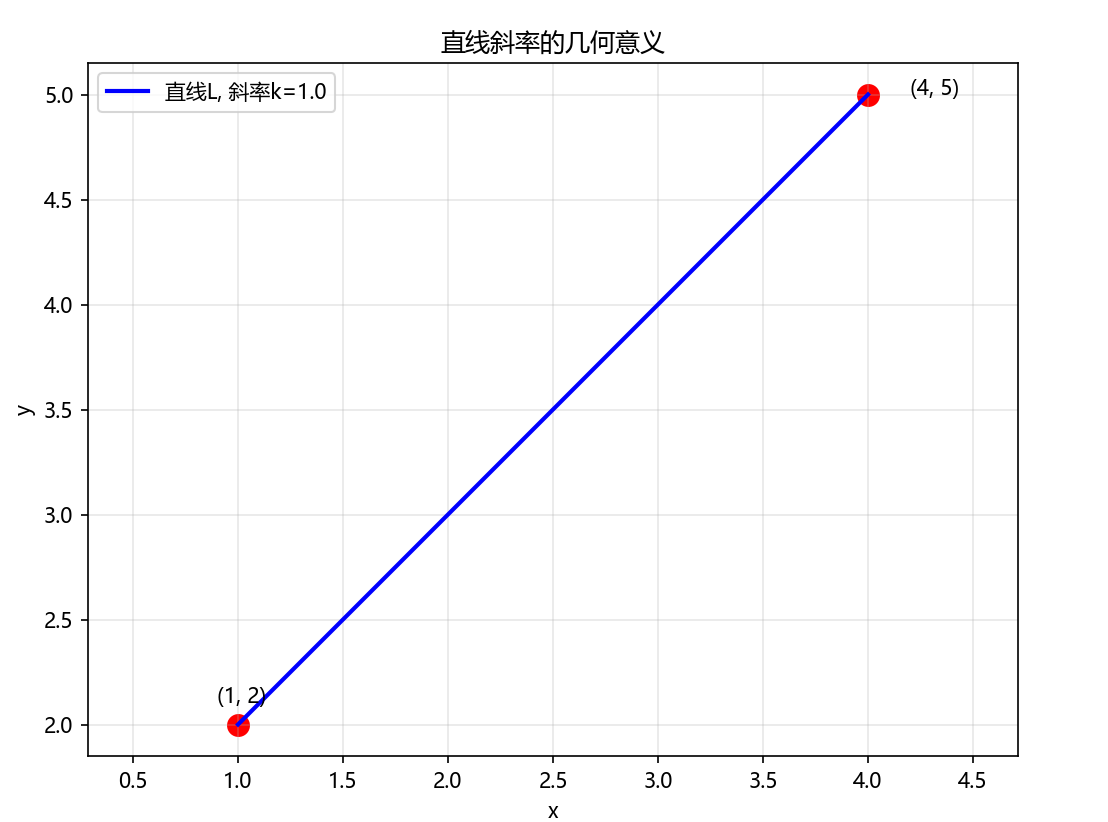
🔍 问题2:运动速度(物理问题)
当质点 PPP 做匀速运动时,若运动距离 sss 与运动时间 ttt 的关系记为 s=s(t)s = s(t)s=s(t),则比值 s(t1)−s(t0)t1−t0\frac{s(t_1) - s(t_0)}{t_1 - t_0}t1−t0s(t1)−s(t0) 表示质点的运动速度。
Python案例:匀速运动模拟
python
def uniform_motion():
"""模拟匀速运动"""
t = np.linspace(0, 10, 100)
s = 2 * t # 匀速运动,速度v=2
plt.figure(figsize=(10, 6))
plt.plot(t, s, 'b-', linewidth=2, label='s(t) = 2t')
# 计算平均速度
t0, t1 = 2, 6
s0, s1 = 2*t0, 2*t1
velocity = (s1 - s0) / (t1 - t0)
plt.scatter([t0, t1], [s0, s1], color='red', s=100)
plt.annotate(f't={t0}, s={s0}', (t0, s0), xytext=(t0, s0-3))
plt.annotate(f't={t1}, s={s1}', (t1, s1), xytext=(t1, s1+1))
plt.title(f'匀速运动:速度v = {velocity}')
plt.xlabel('时间 t'); plt.ylabel('距离 s')
plt.grid(True, alpha=0.3)
plt.legend()
plt.show()
uniform_motion()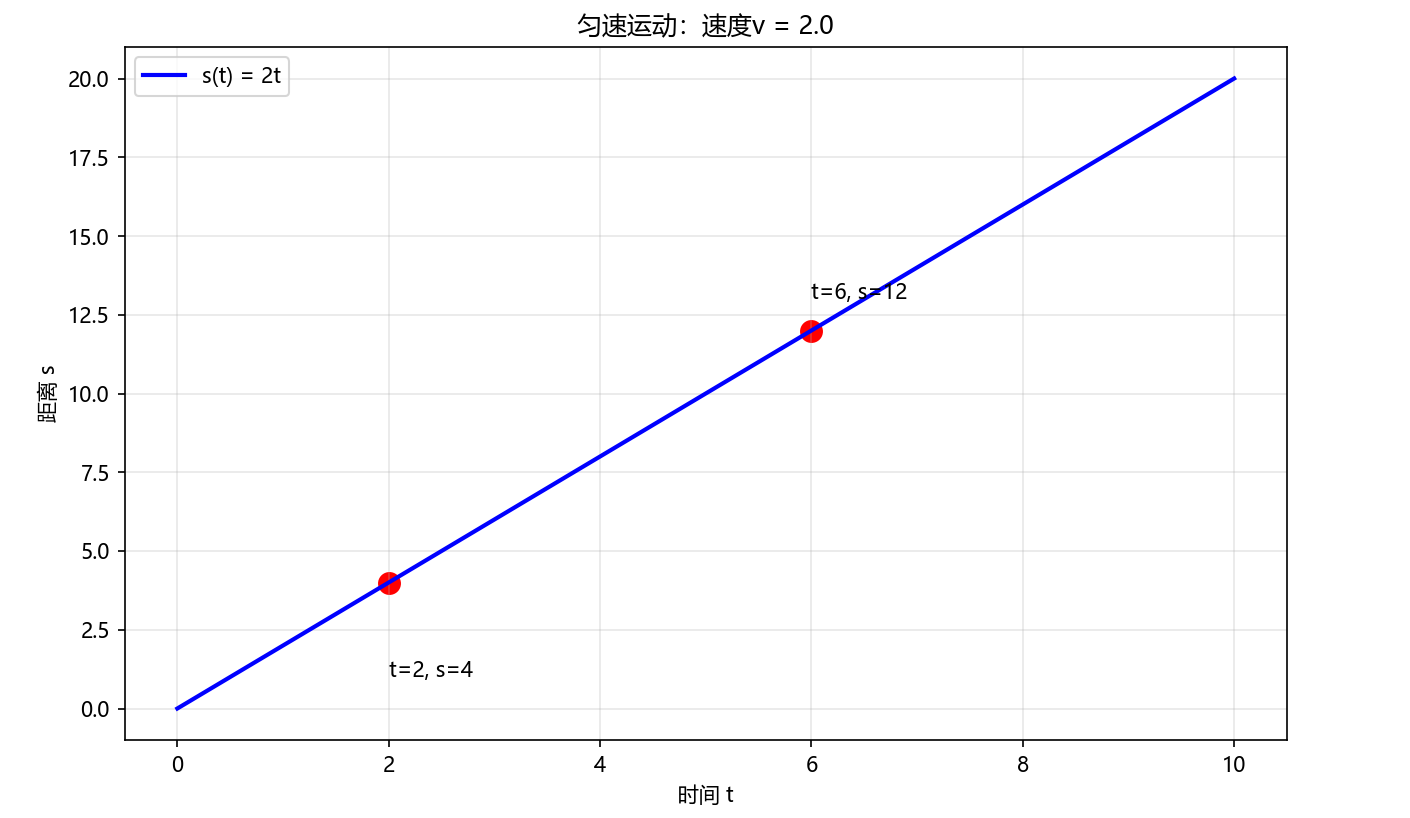
🔍 问题3:线密度(工程问题)
一条质量均匀的细杆,从它的一端量取长度为 lll 的一段,记这段细杆的质量为 m=m(l)m = m(l)m=m(l),则比值 m(l)−m(l0)l−l0\frac{m(l) - m(l_0)}{l - l_0}l−l0m(l)−m(l0) 表示细杆的线密度。
三、从特殊到一般:导数的诞生
关键突破
实际问题中,我们遇到的不仅是:
- ❌ 直线问题 → ✅ 还有曲线问题
- ❌ 匀速运动 → ✅ 还有变速运动
- ❌ 均匀细杆 → ✅ 还有非均匀细杆
核心思想 :当两点无限接近时,平均变化率就变成了瞬时变化率!
数学定义预览
函数 f(x)f(x)f(x) 在点 x0x_0x0 处的导数定义为: f′(x0)=limΔx→0f(x0+Δx)−f(x0)Δxf'(x_0) = \lim_{\Delta x \to 0} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}f′(x0)=Δx→0limΔxf(x0+Δx)−f(x0)
四、Python实战:从平均变化率到瞬时变化率
python
def from_average_to_instantaneous():
"""演示从平均变化率到瞬时变化率的过程"""
# 定义函数:f(x) = x^2
f = lambda x: x**2
x0 = 2
# 不同的Δx值
delta_x_values = [1.0, 0.5, 0.1, 0.01, 0.001]
plt.figure(figsize=(12, 8))
x_curve = np.linspace(0, 4, 1000)
plt.plot(x_curve, f(x_curve), 'b-', linewidth=2, label='f(x) = x²')
for i, dx in enumerate(delta_x_values):
x1 = x0 + dx
slope = (f(x1) - f(x0)) / dx
# 绘制割线
x_line = np.linspace(x0-0.5, x1+0.5, 100)
y_line = f(x0) + slope * (x_line - x0)
plt.plot(x_line, y_line, '--', alpha=0.7,
label=f'Δx={dx}, 斜率={slope:.3f}')
plt.scatter([x0], [f(x0)], color='red', s=100, label=f'点({x0}, {f(x0)})')
plt.title('从平均变化率到瞬时变化率(Δx → 0)')
plt.xlabel('x'); plt.ylabel('f(x)')
plt.legend(); plt.grid(True, alpha=0.3)
plt.show()
from_average_to_instantaneous()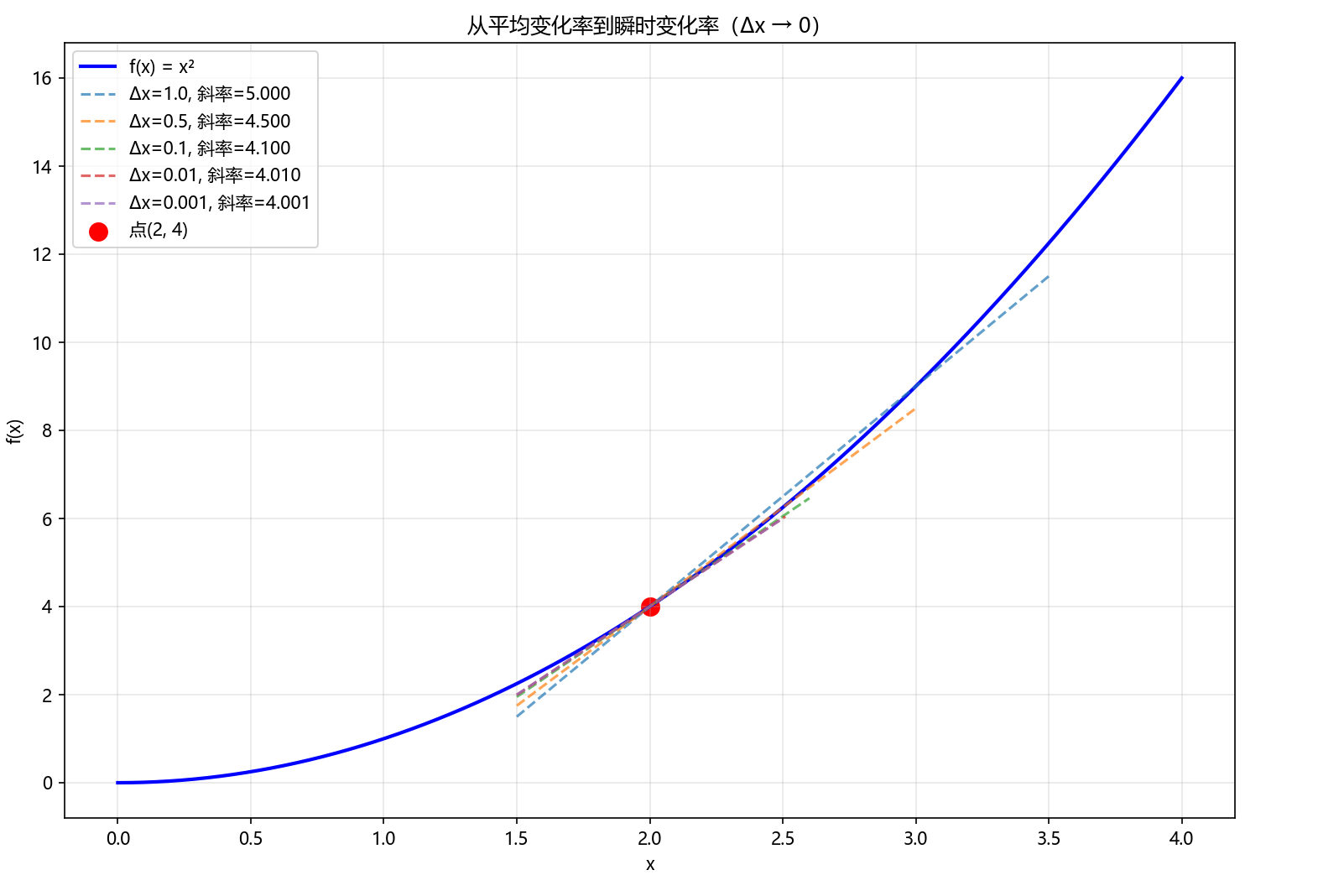
五、核心概念关系图
连续函数 → 平均变化率 → 极限过程 → 导数(瞬时变化率)
↓
微分(局部线性近似)🔍 互动思考题(评论区讨论)
- 几何直观:为什么曲线的切线斜率能够反映函数的变化率?
- 物理意义:瞬时速度与平均速度有什么本质区别?
- 实际应用:你能举出生活中其他需要用到导数概念的实例吗?
- 挑战题:如果函数在某点不可导,它的图像会是什么样子?
💻 Python小挑战
# 挑战1:绘制函数 f(x) = |x| 在x=0处的图像,观察导数情况
# 挑战2:模拟自由落体运动,计算不同时刻的瞬时速度
# 挑战3:用数值方法估算 π 的值(提示:利用圆的切线斜率)六、下节预告
在下一篇文章中,我们将正式学习:
- ✅ 导数的严格数学定义
- ✅ 导数的几何意义和物理意义
- ✅ 可导与连续的关系
- ✅ 基本求导公式和法则
参考资料:扈志明,《微积分》,高等教育出版社
版权声明:本文采用CC BY-NC-SA 4.0协议,欢迎转载但请注明出处。
互动邀请:如果你对导数概念有独特的理解或有相关的应用案例,欢迎在评论区分享讨论!