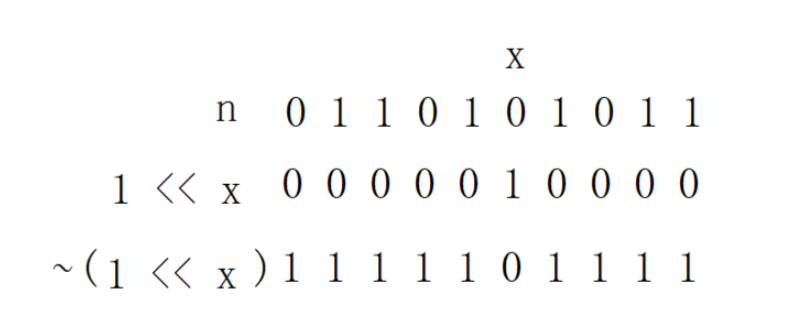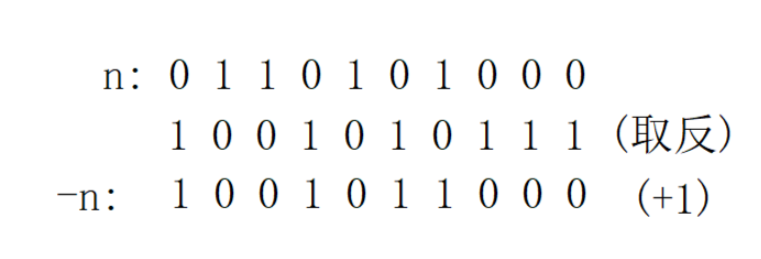一、常见位运算总结
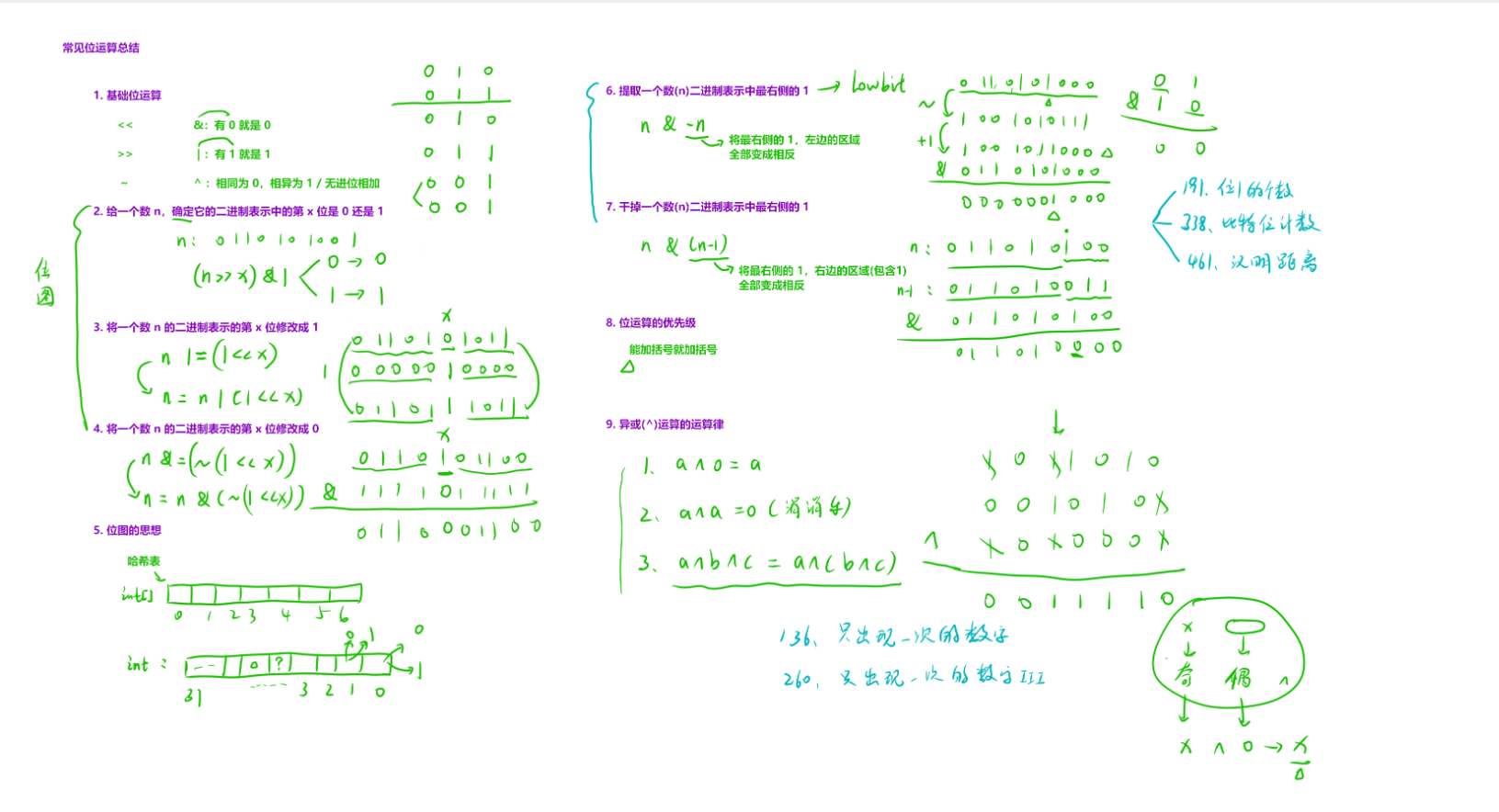
1.1基础位运算
|----------|-------------------------|
| 运算符 | 操作 |
| << | 左移 |
| >> | 右移 |
| ~ | 取反 |
| & | 对应二进制位有0就是0 |
| | | 对应二进制位有1就是1 |
| ^ | 对应二进制位,相同为0相异为1 / 不进位相加 |对于^运算的不进位相加解释:假设为
0 1 0
0 1 1
那么不进位相加就是 0 0 1,这个理解在我们后面是有用的
1.2给一个数n,确定他的二进制位中的第x为是0还是1
利用&(对应二进制位有0就是0)运算即可,将 n >> x后,他的第x为就在最右边,那么此时& 一个1,那么就只会得到1 或 0,如果是1,那么这个位上是1,反之则是0
即 (n>> x) &1
1.3将一个数n的二进制表示的第x位修改为1
方法: n | (1 << x) 即可:
这样,能保证其他位的不变,将对应x位改为1
1.4将一个数n的二进制表示的第x位修改为0
要想将某一位修改为0,那么就让这一位 & 0即可,但是怎么得到仅是这一位为0的数字呢??
方法: 我们将1 << x后取反即可
这样,通过**n & (~(1 << x))**就能得到所求
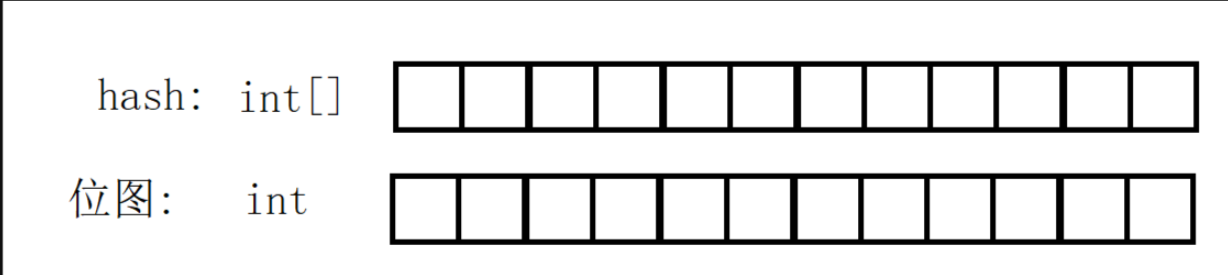
1.5位图的思想
哈希表实际上大多数情况下是个数组,通过数组的内容来存储数据
实际上二进制位同样有这个效果:
通过二进制位上是0还是1来存储信息,而我们上面的1.2 ~ 1.4的方法主要是为了以后操作位图做好准备
1.6提取一个数n二进制表示中最右侧的1
方法:n & -n
-n操作实际上就是将原数取反后 +1 的操作,
这样我们会发现,n与-n相比,原数最右侧的1的左边变成原来相反,右侧则不变,还是0
那么我们将 n & -n后,就能提取出最右侧的1
1.7去掉一个数n二进制表示中最右侧的1
方法: n & (n-1)
- 实际上n-1的操作就是从右往左进行借位的操作,因为在遇到最右侧的1之前,其余位都是0,是不够-1的,那么就要借位,直到遇见1
- 那么n-1后就得到与原来的n相比:最右侧的1(包括这个1)的右侧都是原来的相反数,而左侧的不变
- 那么我们将n & n-1后,就能将原数最右侧的1去掉
1.8异或运算的运算律
实际上我们用前面讲到的不进位相加就能理解
(1)a ^ 0 = a
(2)a ^ a = 0(形象称为消消乐)
(3)a ^ b ^ c = a ^ (b ^ c)
那么不进位相加实际上就是每一列抵消1的过程,既然这样,那就和顺序毫无关系了,因此满足交换律
题目链接:
题目描述:
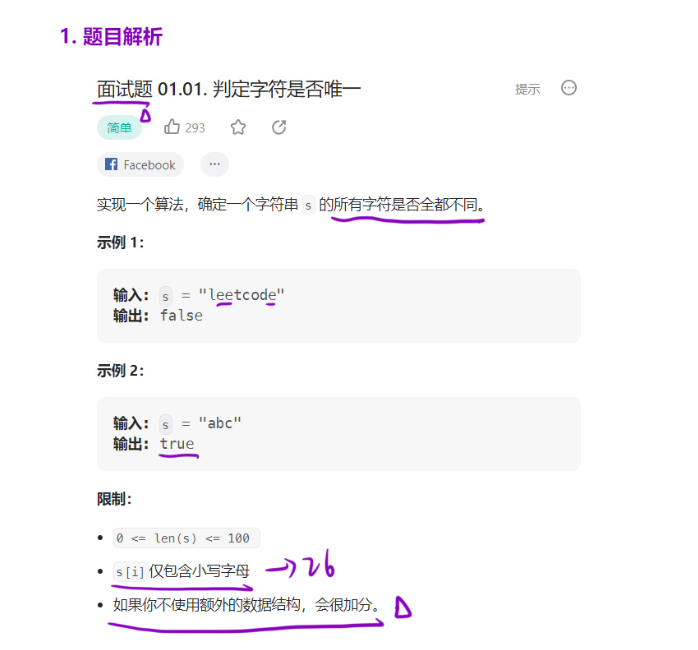
题目解析:
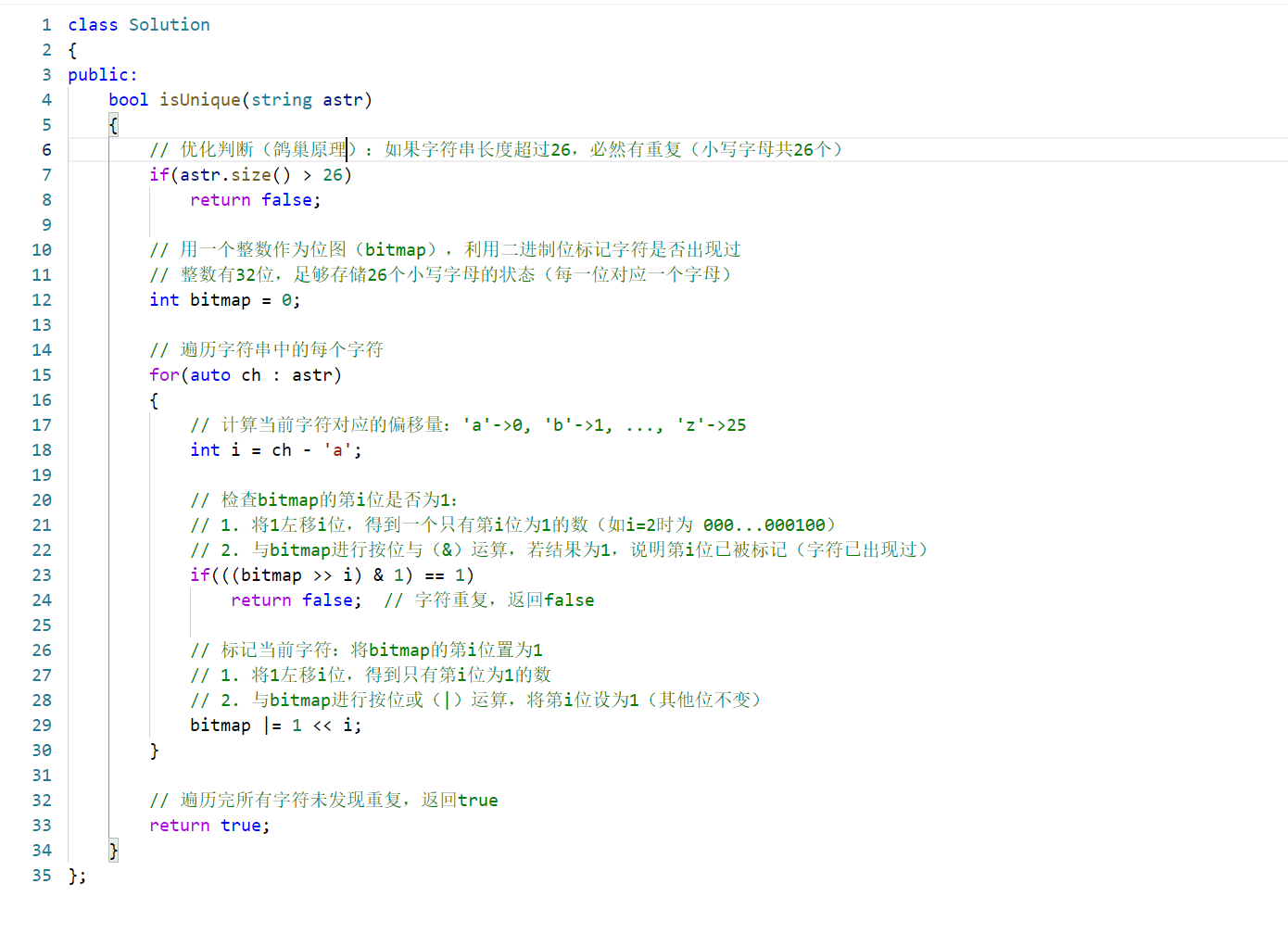
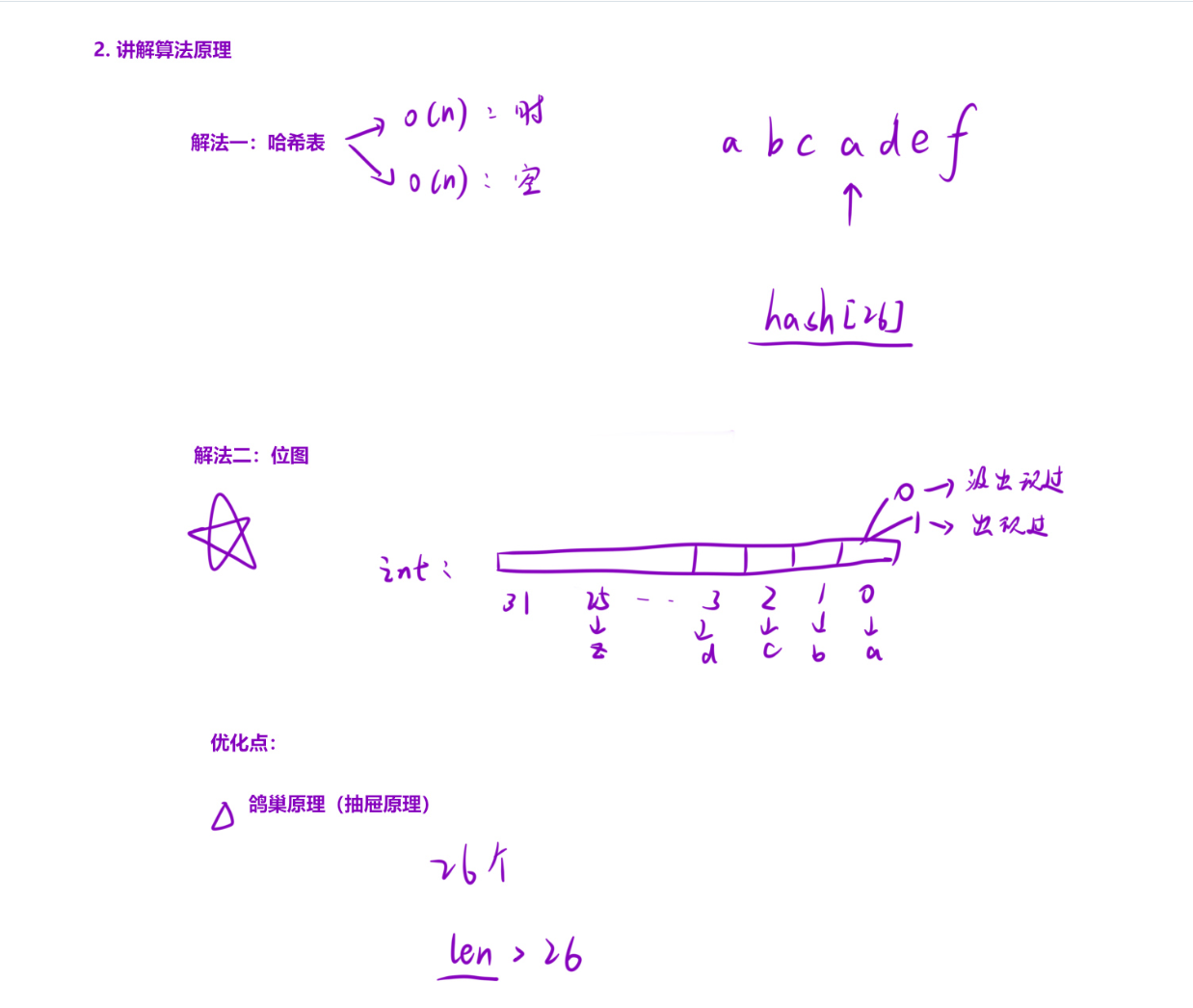
核心逻辑解析:
-
长度优化判断 :由于小写字母只有 26 个,若字符串长度超过 26,必然存在重复字符,直接返回
false,避免后续无效计算。 -
位图(bitmap)原理 :利用整数的二进制位作为 "标记位",每一位对应一个小写字母(第 0 位对应
'a',第 1 位对应'b',...,第 25 位对应'z')。- 例如:
bitmap = 0b101(二进制)表示'a'(第 0 位)和'c'(第 2 位)已出现过。
- 例如:
-
位运算操作:
- 检查字符是否出现 :
(bitmap >> i) & 1将bitmap右移i位,使第i位移动到最低位,再与1按位与,若结果为1,说明该字符已出现。 - 标记字符出现 :
bitmap |= 1 << i将1左移i位得到一个只有第i位为1的数,再与bitmap按位或,将第i位设为1,完成标记。
- 检查字符是否出现 :
复杂度分析:
- 时间复杂度 :O (n),其中
n为字符串长度,仅需遍历一次字符串。 - 空间复杂度 :O (1),仅使用一个整数
bitmap,空间消耗与输入规模无关。
题目链接:
题目描述:

题目解析:

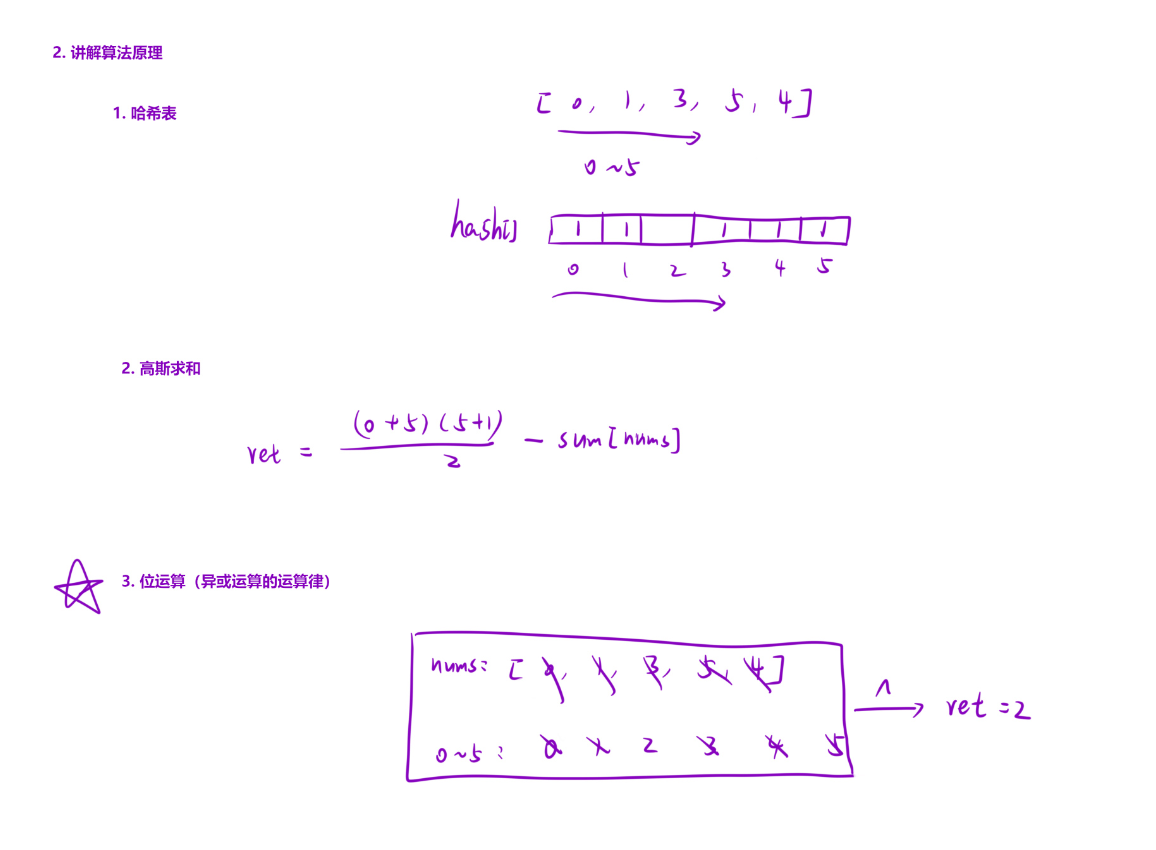
核心原理说明:
-
异或运算的特性:
- 任何数字与自身异或结果为
0(如a ^ a = 0) - 任何数字与
0异或结果为该数字本身(如a ^ 0 = a) - 异或运算满足交换律和结合律(如
a ^ b ^ c = a ^ c ^ b)
- 任何数字与自身异或结果为
-
算法逻辑:
- 假设数组长度为
n,则完整的数字序列应该是0, 1, 2, ..., n(共n+1个数字) - 数组
nums是完整序列中缺少一个数字后的结果(共n个数字) - 当我们把数组中的所有元素与
0~n的所有数字进行异或时:- 完整序列中存在的数字会出现两次(一次在数组中,一次在
0~n中),异或后抵消为0 - 缺失的数字只在
0~n中出现一次,最终会保留在结果中
- 完整序列中存在的数字会出现两次(一次在数组中,一次在
- 假设数组长度为
-
时间复杂度 :
O(n),只需遍历数组一次和0~n一次 -
空间复杂度 :
O(1),只使用了常数个额外变量