MATLAB基于自适应动态特征加权的K-means算法

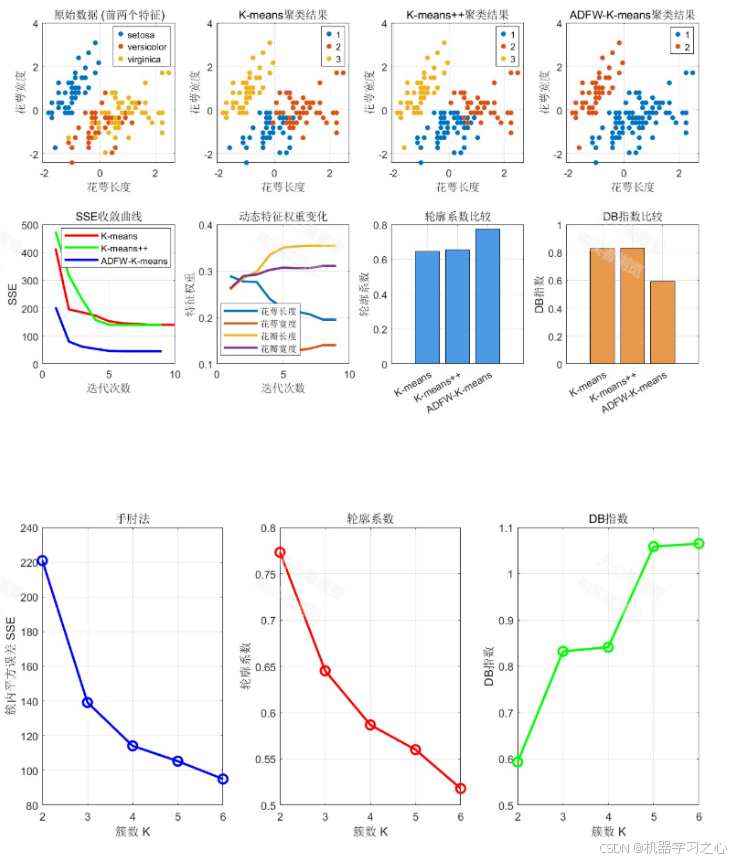
1. 算法核心思想

传统K-means算法中所有特征在距离计算中具有相同权重，而自适应动态特征加权K-means通过为每个特征分配不同的权重，并在迭代过程中动态调整，从而提高聚类性能。

2. 算法原理

2.1 目标函数

J(W,Z,Λ)=∑i=1n∑k=1Kuik∑j=1dλkjβ(xij−zkj)2 J(W,Z,\Lambda) = \sum_{i=1}^n \sum_{k=1}^K u_{ik} \sum_{j=1}^d \lambda_{kj}^\beta (x_{ij} - z_{kj})^2 J(W,Z,Λ)=i=1∑nk=1∑Kuikj=1∑dλkjβ(xij−zkj)2

其中：

• uiku_{ik}uik ∈ {0,1}：样本i属于簇k的指示变量
• zkjz_{kj}zkj：簇k在特征j上的中心
• λkj\lambda_{kj}λkj：簇k中特征j的权重
• β\betaβ > 1：权重指数参数

2.2 特征权重更新公式

λkj=1∑l=1d[DkjDkl]1/(β−1) \lambda_{kj} = \frac{1}{\sum_{l=1}^d \left[ \frac{D_{kj}}{D_{kl}} \right]^{1/(\beta-1)}} λkj=∑l=1d[DklDkj]1/(β−1)1

其中：
Dkj=∑i=1nuik(xij−zkj)2D_{kj} = \sum_{i=1}^n u_{ik}(x_{ij} - z_{kj})^2Dkj=∑i=1nuik(xij−zkj)2

2.3 自适应权重调节

λkj(t+1)=αλkj(t)+(1−α)exp⁡(−γDkj)∑l=1dexp⁡(−γDkl) \lambda_{kj}^{(t+1)} = \alpha \lambda_{kj}^{(t)} + (1-\alpha) \frac{\exp(-\gamma D_{kj})}{\sum_{l=1}^d \exp(-\gamma D_{kl})} λkj(t+1)=αλkj(t)+(1−α)∑l=1dexp(−γDkl)exp(−γDkj)

3. 算法步骤

输入：数据集X, 聚类数K, 最大迭代次数T, 权重指数β
输出：聚类标签, 聚类中心, 特征权重矩阵

1. 初始化：
   - 随机选择K个初始聚类中心
   - 初始化特征权重λ_{kj} = 1/d
   
2. For t = 1 to T:
   a. 分配步骤：
      对每个样本x_i，计算到各聚类中心的加权距离：
      d_{ik} = ∑_{j=1}^d λ_{kj}^β (x_{ij} - z_{kj})^2
      将x_i分配到距离最近的簇
   
   b. 更新步骤：
      重新计算聚类中心：
      z_{kj} = (∑_{i=1}^n u_{ik}x_{ij}) / (∑_{i=1}^n u_{ik})
   
   c. 权重更新步骤：
      计算每个簇中每个特征的离散度：
      D_{kj} = ∑_{i=1}^n u_{ik}(x_{ij} - z_{kj})^2
      更新特征权重：
      λ_{kj} = 1 / ∑_{l=1}^d [D_{kj}/D_{kl}]^{1/(β-1)}
   
   d. 收敛判断：
      如果聚类分配不再变化或目标函数变化小于阈值，则停止
   
3. 返回最终结果

4. MATLAB代码实现

function [labels, centers, weights, obj_history] = adaptive_weighted_kmeans(X, K, max_iter, beta)
% 自适应动态特征加权K-means算法
% 输入：
%   X: n×d数据矩阵
%   K: 聚类数目
%   max_iter: 最大迭代次数
%   beta: 权重指数参数(>1)
% 输出：
%   labels: 聚类标签
%   centers: 聚类中心
%   weights: 特征权重矩阵(K×d)
%   obj_history: 目标函数历史

[n, d] = size(X);

% 1. 初始化
% 随机选择初始中心
rng(1); % 设置随机种子保证可重复性
idx = randperm(n, K);
centers = X(idx, :);

% 初始化权重矩阵
weights = ones(K, d) / d;

% 存储目标函数值
obj_history = zeros(max_iter, 1);

% 2. 迭代过程
for iter = 1:max_iter
    % a. 分配步骤
    distances = zeros(n, K);
    for k = 1:K
        % 计算加权欧氏距离
        weighted_diff = (X - centers(k, :)).^2 * (weights(k, :)'.^beta);
        distances(:, k) = sqrt(weighted_diff);
    end
    [~, labels] = min(distances, [], 2);
    
    % b. 更新聚类中心
    old_centers = centers;
    for k = 1:K
        cluster_points = X(labels == k, :);
        if ~isempty(cluster_points)
            centers(k, :) = mean(cluster_points, 1);
        end
    end
    
    % c. 更新特征权重
    for k = 1:K
        cluster_points = X(labels == k, :);
        if ~isempty(cluster_points)
            % 计算每个特征的离散度
            D_k = sum((cluster_points - centers(k, :)).^2, 1);
            D_k(D_k == 0) = eps; % 避免除零
            
            % 更新权重
            for j = 1:d
                denominator = sum((D_k(j) ./ D_k).^(1/(beta-1)));
                weights(k, j) = 1 / denominator;
            end
        end
    end
    
    % d. 计算目标函数值
    obj_val = 0;
    for k = 1:K
        cluster_points = X(labels == k, :);
        if ~isempty(cluster_points)
            for j = 1:d
                obj_val = obj_val + weights(k, j)^beta * ...
                    sum((cluster_points(:, j) - centers(k, j)).^2);
            end
        end
    end
    obj_history(iter) = obj_val;
    
    % e. 收敛判断
    if iter > 1 && abs(obj_history(iter) - obj_history(iter-1)) < 1e-6
        obj_history = obj_history(1:iter);
        break;
    end
    
    % 显示进度
    fprintf('迭代 %d, 目标函数值: %.6f\n', iter, obj_val);
end

% 绘制目标函数收敛曲线
figure;
plot(1:length(obj_history), obj_history, 'b-', 'LineWidth', 2);
xlabel('迭代次数');
ylabel('目标函数值');
title('自适应加权K-means收敛曲线');
grid on;
end

5. 改进版本：基于信息熵的权重调节

function weights = update_weights_entropy(X, centers, labels, K, alpha)
% 基于信息熵的特征权重更新
% alpha: 熵调节参数

[n, d] = size(X);
weights = zeros(K, d);

for k = 1:K
    cluster_mask = (labels == k);
    if sum(cluster_mask) == 0
        weights(k, :) = 1/d;
        continue;
    end
    
    cluster_data = X(cluster_mask, :);
    center_k = centers(k, :);
    
    % 计算特征重要性得分
    feature_scores = zeros(1, d);
    for j = 1:d
        % 基于类内距离的特征得分
        intra_var = var(cluster_data(:, j));
        if intra_var == 0
            feature_scores(j) = 1;
        else
            feature_scores(j) = 1 / (1 + intra_var);
        end
    end
    
    % 基于信息熵的权重调节
    scores_normalized = feature_scores / sum(feature_scores);
    entropy_weights = exp(-alpha * scores_normalized);
    
    weights(k, :) = entropy_weights / sum(entropy_weights);
end
end

6. 参数设置建议

% 推荐参数范围
K = 3;              % 聚类数目，根据实际数据确定
max_iter = 100;     % 最大迭代次数
beta = 2;           % 权重指数，通常取2-3
alpha = 0.1;        % 熵调节参数

% 调用示例
[labels, centers, weights, obj_history] = adaptive_weighted_kmeans(X, K, max_iter, beta);

7. 算法优势

1. 特征选择能力：自动识别对聚类重要的特征
2. 自适应学习：权重在迭代过程中动态调整
3. 鲁棒性：对噪声特征具有更好的容忍度
4. 可解释性：权重矩阵提供特征重要性的直观理解

完整代码私信MATLAB基于自适应动态特征加权的K-means算法