什么是算法复杂度？

在计算机科学中，当我们谈论"算法"的时候，不仅仅在关心它能否解决问题，还关心它用多快的速度解决问题 以及需要多少资源 。这里的资源主要是时间和空间。算法复杂度，就是衡量算法消耗这些资源的指标。

一、算法复杂度的两大类

算法复杂度主要分为 时间复杂度 和 空间复杂度：

1. 时间复杂度（Time Complexity）

时间复杂度衡量算法执行所需的时间，通常与输入数据的规模 (n) 有关。我们通常用 大 O 表示法（Big O Notation） 来描述算法的增长趋势，而不是精确时间。

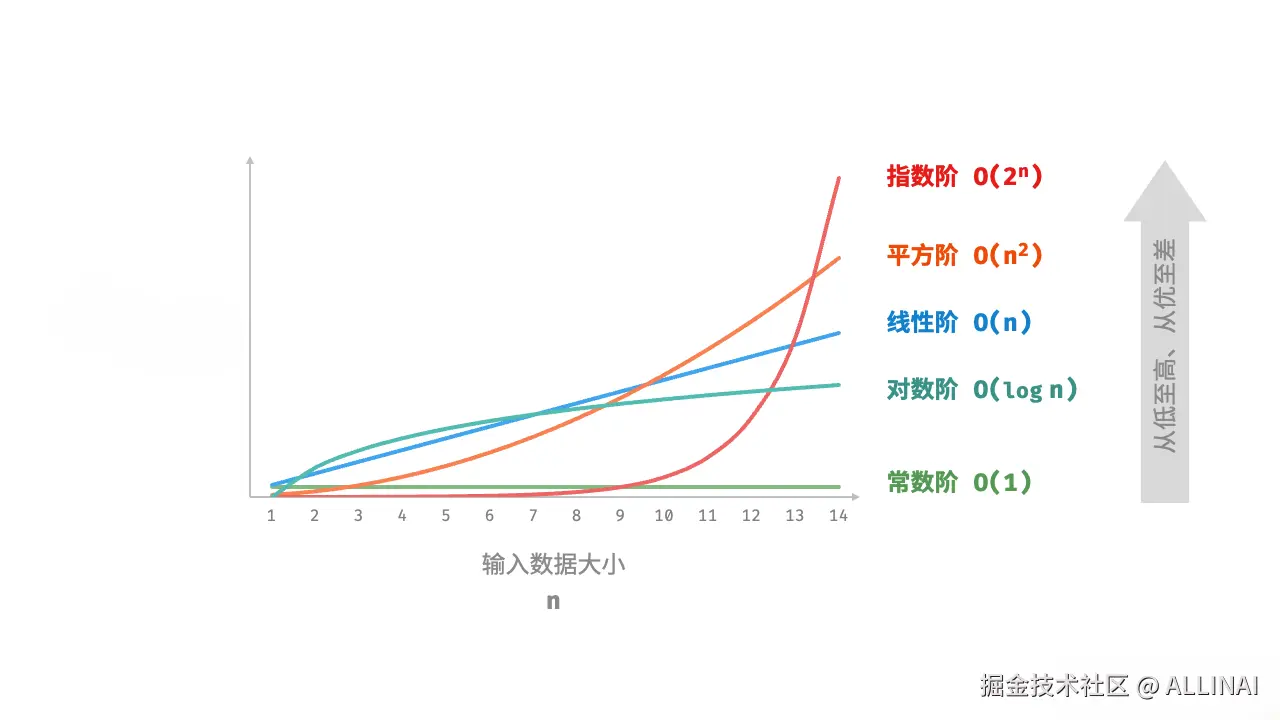
常见例子：

O(1) - 常数时间

python 复制代码

def get_first_element(arr):
    return arr[0]  # 无论数组多大，访问第一个元素只需一步

O(n) - 线性时间

python 复制代码

def sum_list(arr):
    total = 0
    for num in arr:  # 遍历每个元素，操作次数随n线性增长
        total += num
    return total

O(n^2) - 平方时间

python 复制代码

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n-i-1):  # 嵌套循环，操作次数约为n²
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]

O(log n) - 对数时间（二分查找）

python 复制代码

def binary_search(arr, target):
    left, right = 0, len(arr) - 1
    while left <= right:
        mid = (left + right) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return -1

O(n log n) - 线性对数时间（Python 内置排序）

python 复制代码

arr = [5, 2, 9, 1, 5, 6]
arr.sort()  # 底层使用 Timsort，时间复杂度 O(n log n)

2. 空间复杂度（Space Complexity）

空间复杂度衡量算法运行时占用的内存量，通常也依赖于输入规模。

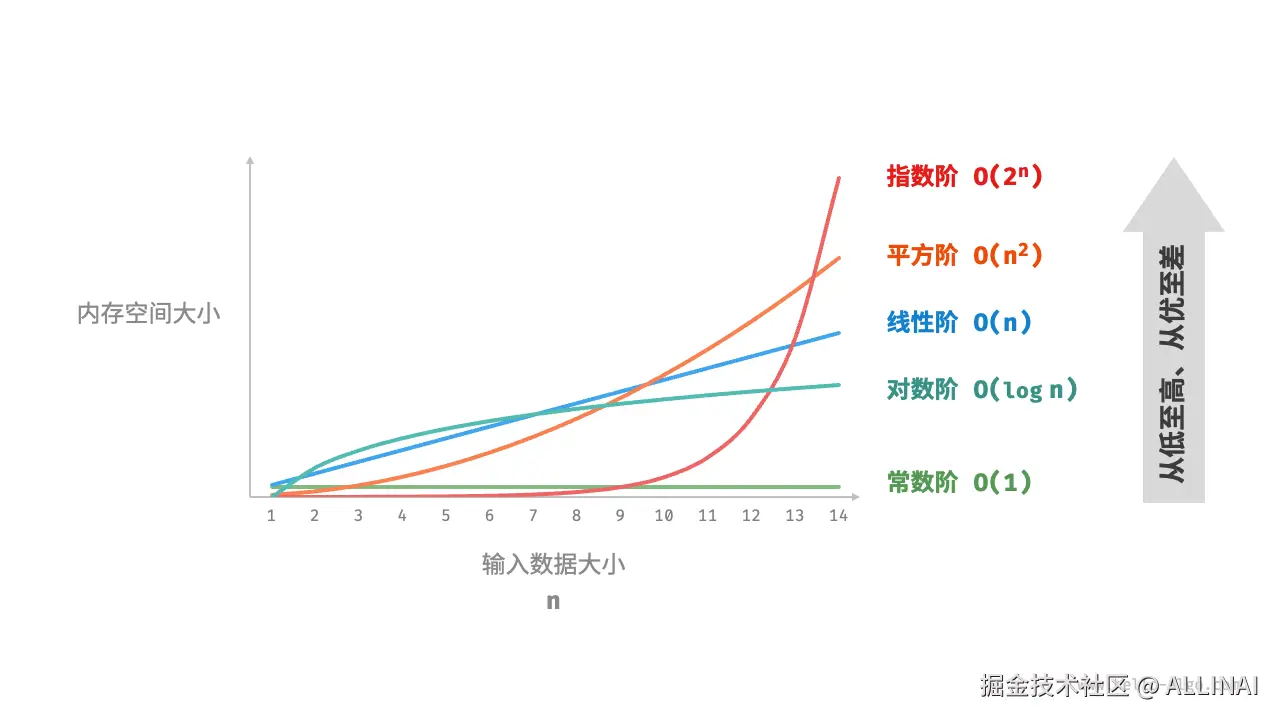
python 复制代码

# O(n) - 需要额外数组存储
def duplicate_list(arr):
    return arr.copy()  # 创建了一个与原数组等大的副本

python 复制代码

# O(1) - 原地交换
def swap_first_two(arr):
    if len(arr) >= 2:
        arr[0], arr[1] = arr[1], arr[0]  # 不使用额外空间

二、为什么算法复杂度重要？

算法复杂度直接影响程序的效率和可扩展性：

处理大数据：在数据量巨大的情况下，低效算法可能让程序运行几小时甚至几天，而高效算法只需几分钟。
优化资源使用：在内存有限的设备上，低空间复杂度算法更适用。
预测性能：通过分析复杂度，我们可以在实际运行前预测程序的表现。

三、常见复杂度对比

复杂度	增长趋势	举例
O(1)	恒定	访问数组元素
O(log n)	对数	二分查找
O(n)	线性	遍历数组
O(n log n)	线性对数	快速排序、归并排序
O(n²)	平方	嵌套循环排序（冒泡、选择）
O(2^n)	指数	递归解子集问题
O(n!)	阶乘	全排列生成

从表格可以看出，输入规模增加时，算法效率的差异可能会非常巨大。

四、总结

算法复杂度是评价算法效率的重要指标，包括时间和空间两个方面。结合 Python 示例，我们可以更清楚地看到算法执行时的资源消耗趋势。理解复杂度，就像掌握了算法性能的"体温计"，能提前预测和优化程序的表现。