机器学习(3)---线性算法，决策树，神经网络，支持向量机

杭州杭州杭州2025-10-30 21:27

1、概述

  1. 数据集

最常用的公开数据集

  • 数据集 dataset
  • 样本 sample
  • 特征 feature
  • 类别标记 label
  • 向量 vector
  • 矩阵 matrix
  1. 机器学习的任务
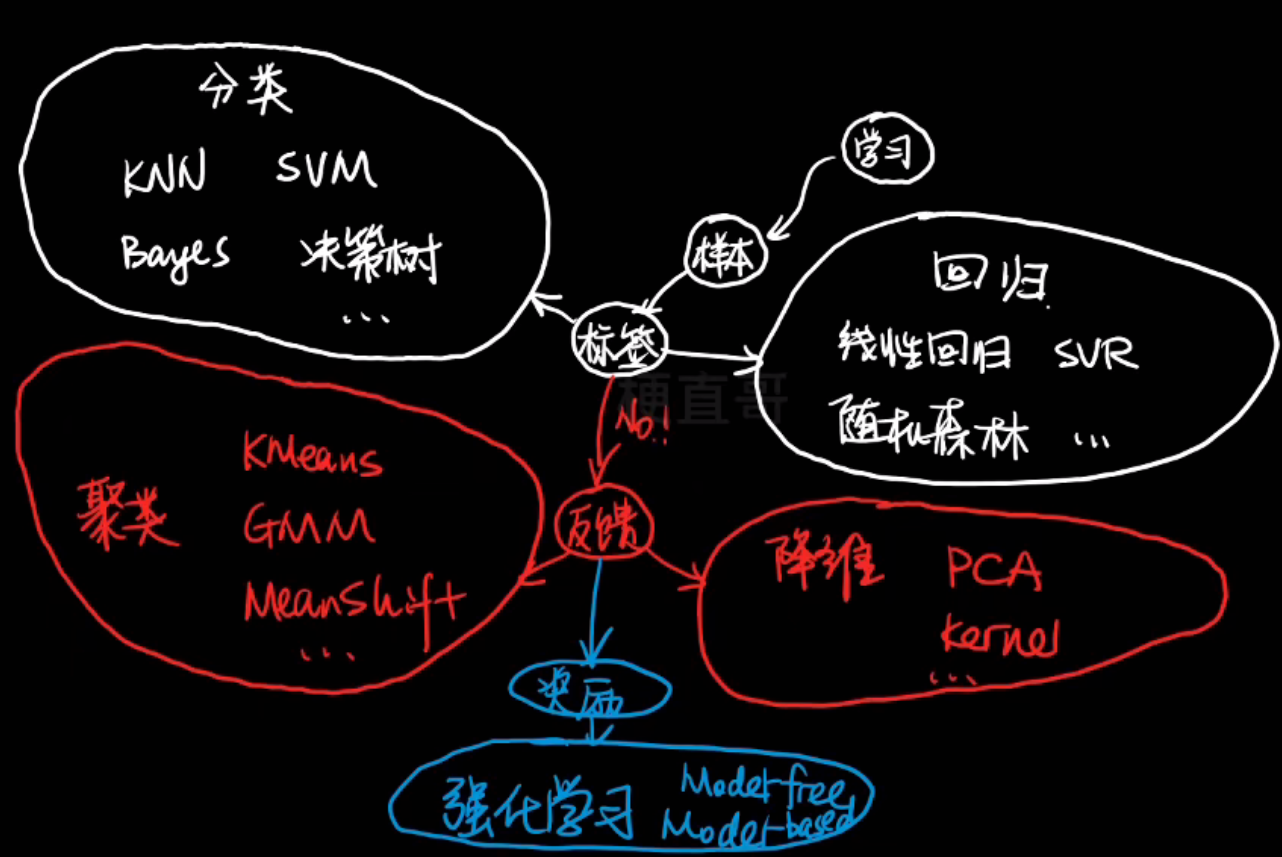
  • 分类任务：已知样本特征，判断样本类别。常见有二分类，多分类，多标签分类
    • 二分类-----垃圾邮件分类，图片识别
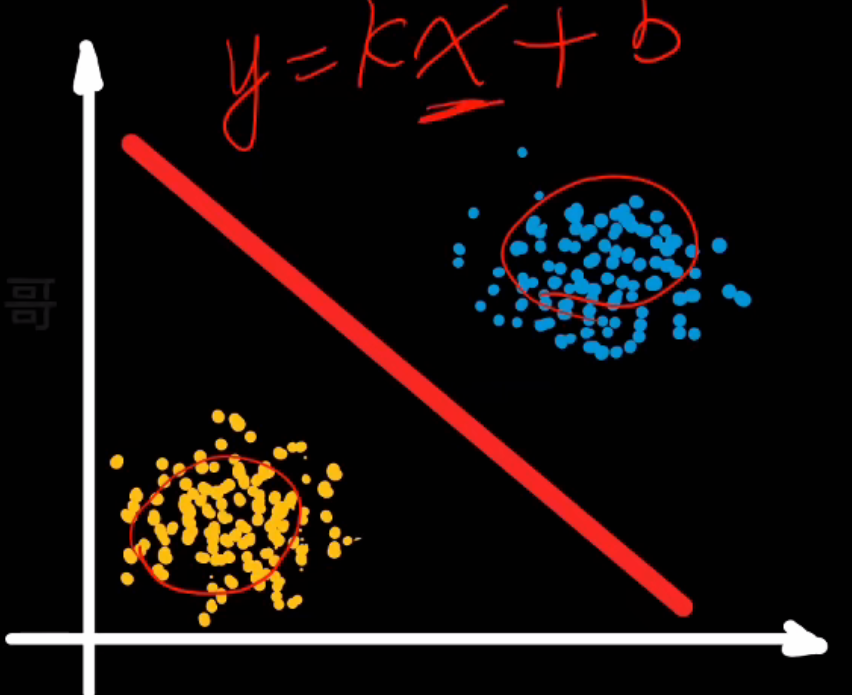
    • 多分类：病毒分型
    • 多标签分类：标签间不互斥，概率和不为1（行人，车辆，物体）
  • 回归任务
    • 线性回归
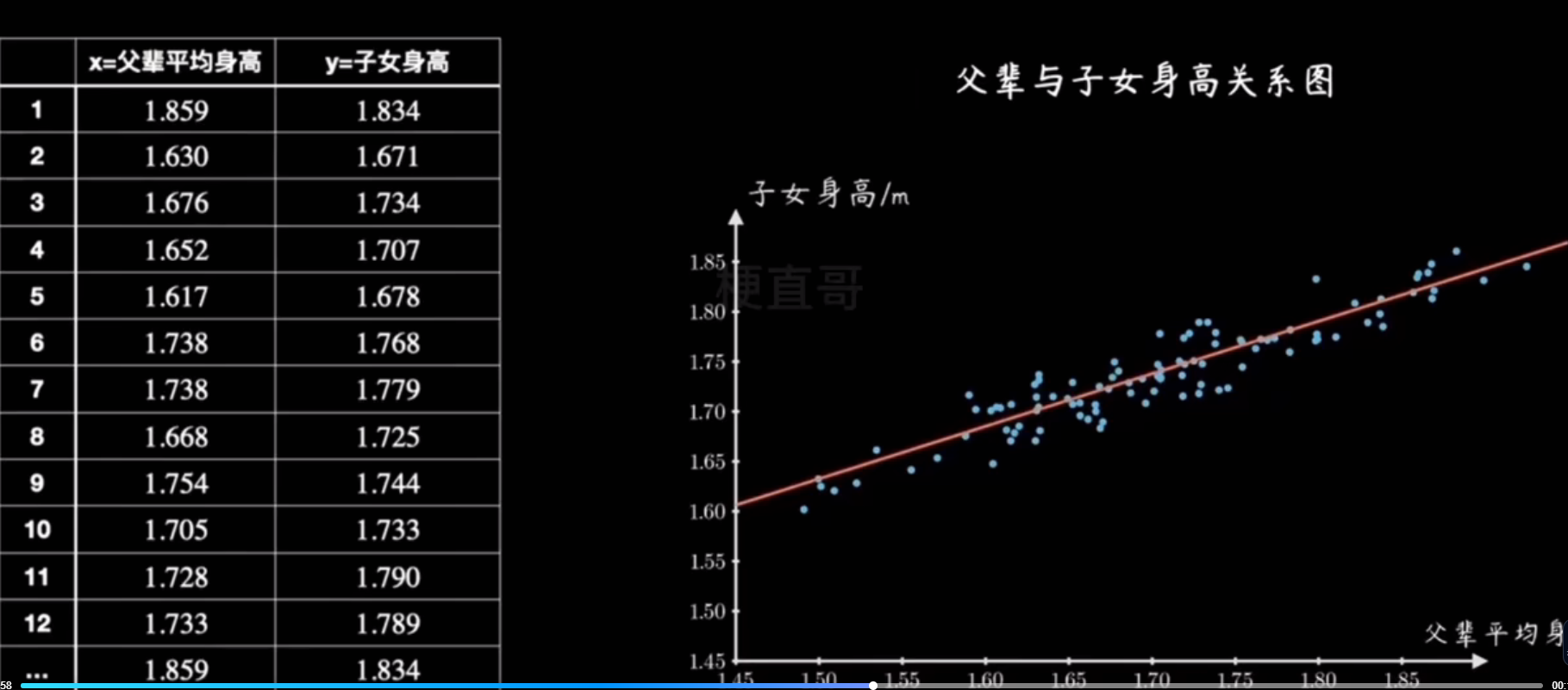
    • 多项式回归
    • 逻辑回归

分类和回归都是监督学习，因为二者的数据集都有标签，有直接的反馈

  1. 机器学习分类

分类依据

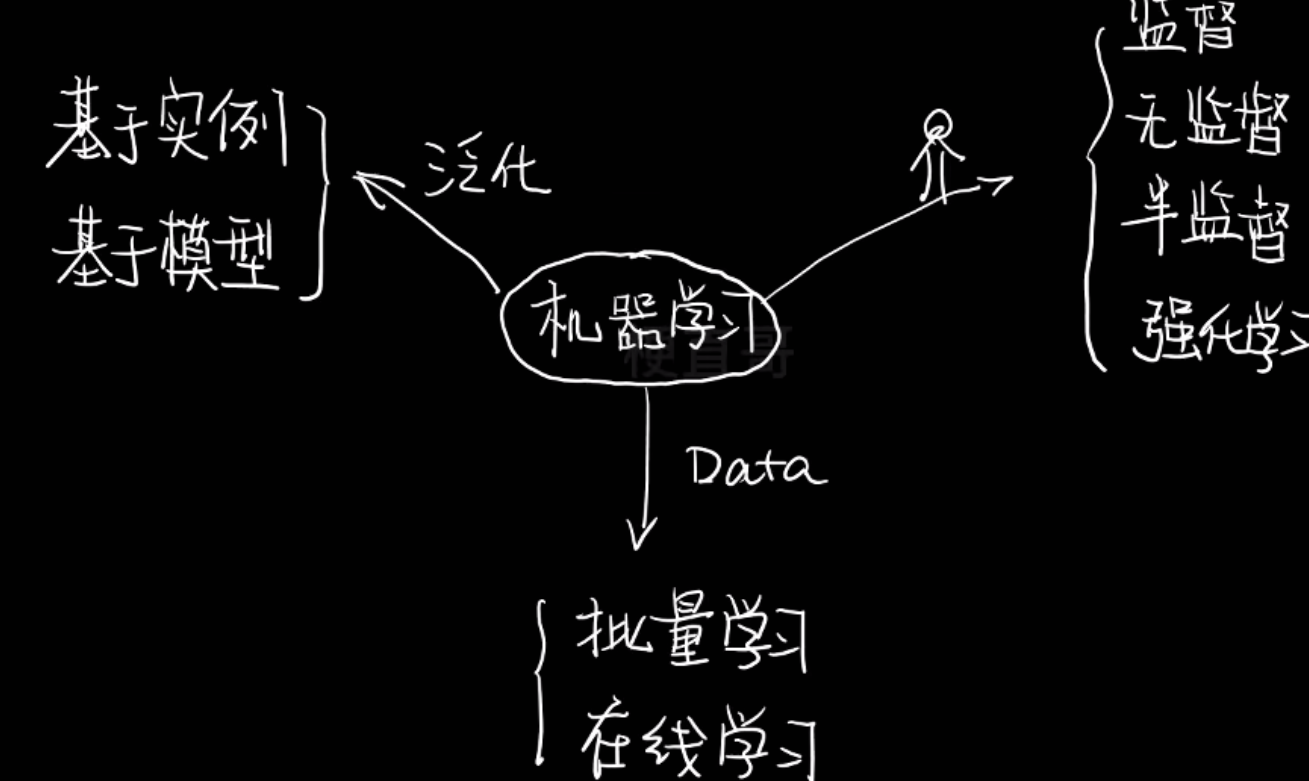
按训练数据中是否有标签（以及反馈信号的类型）分：

  • 监督学习
    • 分类和回归
    • 训练数据有标记
    • 基础且重要
  • 无监督学习
    • 训练数据未经标记
    • 聚类：K均值算法（K-means），密度聚类（DBSCAN），最大期望算法
    • 降维(主成分分析PCA,核方法)
    • 关联规则学习：挖掘特征间关联关系，用Apriori方法和Eclat方法
  • 半监督学习
    • 少量标记数据
    • 大量无标记数据
  • 强化学习
    • 观测环境，估计状态，执行操作，获得回报或惩罚

按 学习方式/数据输入方式 来分

  • 批量学习
    • 先训练再使用，需要大量的时间和计算资源
    • 通常是离线完成
  • 在线学习
    • 循序渐进，边学边用

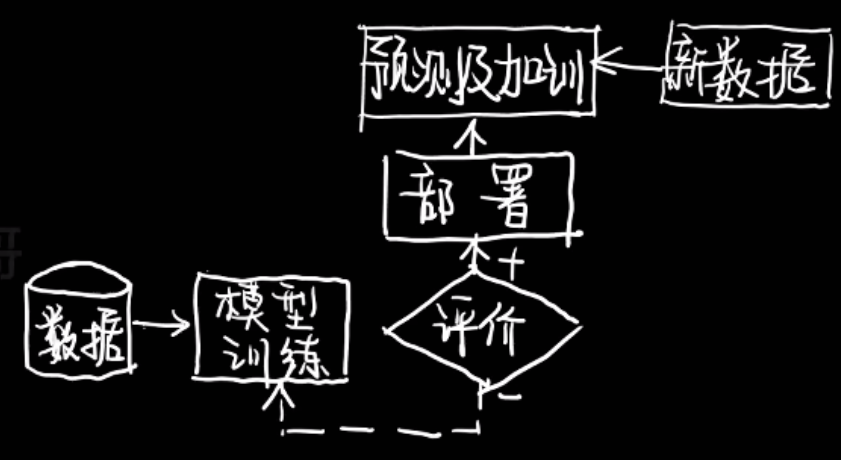
按怎么泛化来分

  • 基于实例的学习
    • 不同的泛化方式，先记住训练实例
    • 相似度的学习
  • 基于模型的学习
    • 先构建模型，然后预测
  1. 常见误区
  • 数据不是越多越好，多并不意味着准确，传统算法依旧有用
  • 模型训练出来不一定可用， 深度学习是个黑盒子
  • 机器学习本质是统计，确定性依旧很重要，我们要平衡好随机与确定性的平衡
  • 机器学习适合大数据，很多问题天然小数据，小样本学习是挑战也是机会
  • 机器学习尚在判断阶段，抽象思维和逻辑推理远未实现
  • 自动驾驶伤了人算谁的错，机器的道德规范是什么
  • 机器学习不死，深度学习局限性很大，其本质是空间几何变换
  1. 软件的使用
  • Anaconda命令行
    • conda -V
    • 更新conda update conda
    • 查看有多少个虚拟环境：conda env list
    • 创建虚拟环境：conda create -n 名字 python=3.10
    • 激活环境：conda activate 名字
    • 查看当前环境已经安装的包：conda list
    • 装包:conda install 包名
    • 删除包：conda uninstall 包名
    • 装可视化界面：conda install jupyter notebook
    • 启动：jupyter notebook
    • 删除安装的虚拟环境：conda deactivate（先退出创建的虚拟环境）,conda remove -n 名字 --all

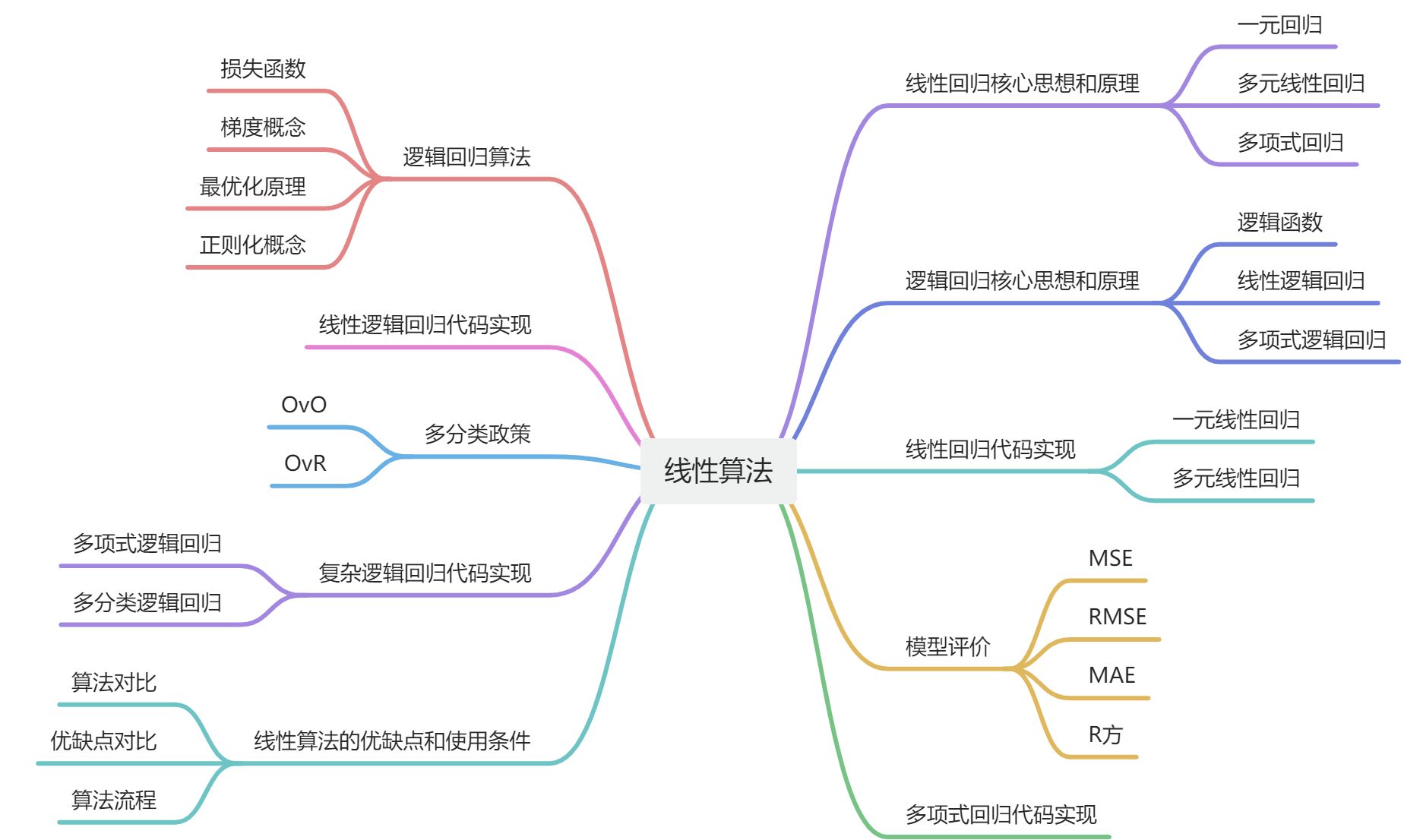
2、线性算法

回归就是找条线

类型 代表算法 主要功能 损失函数 特点
回归任务 线性回归（Linear Regression） 预测连续值（如房价、气温） 均方误差（MSE） 最经典的线性模型
岭回归（Ridge Regression） 回归 + L2正则化 MSE + λ‖w‖² 抑制过拟合
分类任务 逻辑回归（Logistic Regression） 二分类（如生存/死亡） 交叉熵损失 "回归"名字但做分类
线性判别分析（LDA） 二分类或多分类 最大化类间方差比 有概率解释

线性回归

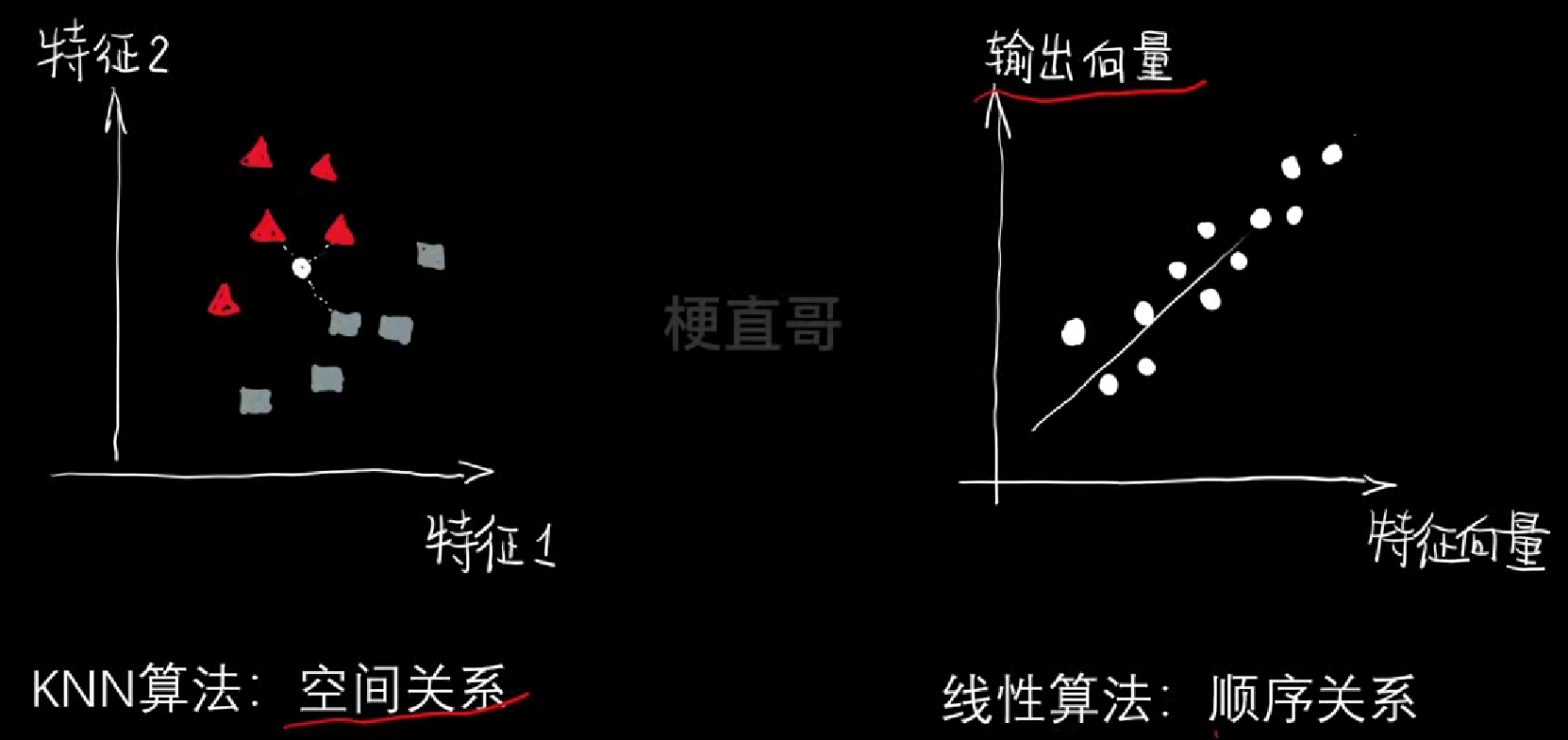
  • 距离"误差"
  • 损失函数
  • 最优化

先导入数据集

python 复制代码 
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
import warnings
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler

warnings.filterwarnings("ignore")

housing = datasets.fetch_california_housing()

print(housing.DESCR)

# 选择第一个特征（中位数收入）作为一元线性回归的特征
x = housing.data[:, 0]  # MedInc - 中位数收入
y = housing.target

# 限制数据范围以便更好地展示
x = x[y < 5]
y = y[y < 5]

plt.scatter(x, y)
plt.xlabel('Median Income')
plt.ylabel('House Price')
plt.title('California Housing: Income vs Price')
plt.show()

# 数据分割
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=0)

plt.scatter(x_train, y_train)
plt.xlabel('Median Income')
plt.ylabel('House Price')
plt.title('Training Data')
plt.show()
  1. 一元线性回归

y=kx+b

最优化问题，民主投票，距离的衡量

代码实现

  • 一元线性回归公式实现
python 复制代码 
## 
def fit(x, y):
    a_up = np.sum((x - np.mean(x)) * (y - np.mean(y)))
    a_bottom = np.sum((x - np.mean(x)) ** 2)
    a = a_up / a_bottom
    b = np.mean(y) - a * np.mean(x)
    return a, b

a, b = fit(x_train, y_train)
print(f"斜率 a: {a}")
print(f"截距 b: {b}")

plt.scatter(x_train, y_train)
plt.plot(x_train, a * x_train + b, c='r')
plt.xlabel('Median Income')
plt.ylabel('House Price')
plt.title('Manual Linear Regression - Training')
plt.show()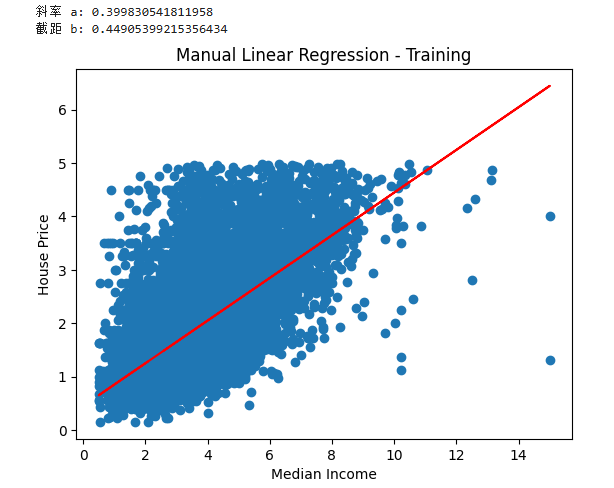

用测试集试试效果

python 复制代码 
plt.scatter(x_test, y_test)
plt.plot(x_test, a * x_test + b, c='r')
plt.xlabel('Median Income')
plt.ylabel('House Price')
plt.title('Manual Linear Regression - Testing')
plt.show()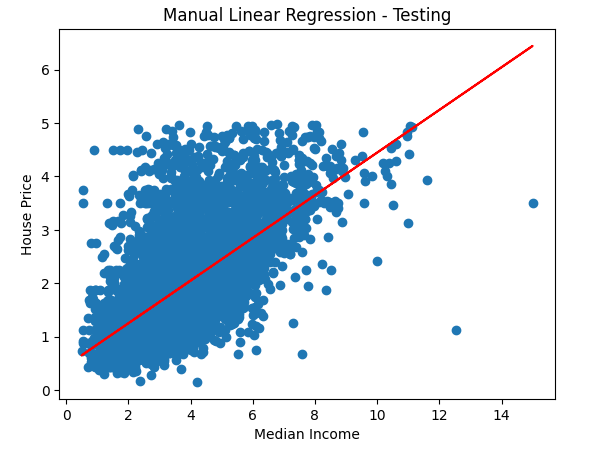
  • sklearn实现一元线性回归
python 复制代码 
## sklearn实现一元线性回归
lin_reg = LinearRegression()
# reshape(-1, 1) 把一维数组变成二维数组
lin_reg.fit(x_train.reshape(-1, 1), y_train)

y_predict = lin_reg.predict(x_test.reshape(-1, 1))

plt.scatter(x_test, y_test)
plt.plot(x_test, y_predict, c='r')
plt.xlabel('Median Income')
plt.ylabel('House Price')
plt.title('Sklearn Linear Regression - Testing')
plt.show()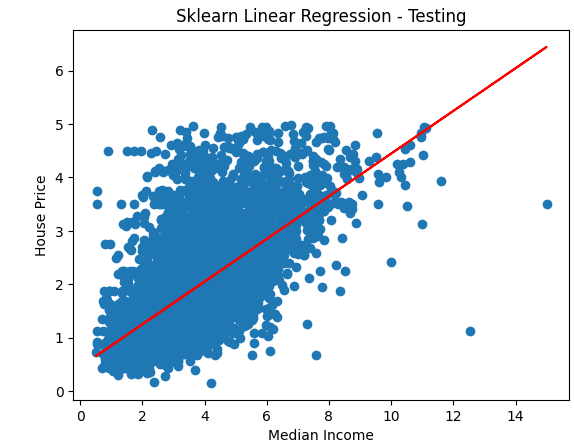
  1. 多元线性回归
python 复制代码 
## sklearn 实现多元线性回归
# 使用所有特征
x_multi = housing.data
y_multi = housing.target

# 限制数据范围
x_multi = x_multi[y_multi < 5]
y_multi = y_multi[y_multi < 5]

x_train_multi, x_test_multi, y_train_multi, y_test_multi = train_test_split(
    x_multi, y_multi, test_size=0.3, random_state=0
)

lin_reg_multi = LinearRegression()
lin_reg_multi.fit(x_train_multi, y_train_multi)

score = lin_reg_multi.score(x_test_multi, y_test_multi)
print(f"多元线性回归 R² 分数: {score}")

输出：
多元线性回归 R² 分数: 0.5582591396048222

此处不需要归一化，没啥区别

因为多元线性回归学习的是每个特征的权重（系数），模型会自动调整这些权重来适应不同特征的数据尺度

python 复制代码 
## 归一化
standardScaler = StandardScaler()
standardScaler.fit(x_train_multi)
x_train_scaled = standardScaler.transform(x_train_multi)
x_test_scaled = standardScaler.transform(x_test_multi)

lin_reg_scaled = LinearRegression()
lin_reg_scaled.fit(x_train_scaled, y_train_multi)

score_scaled = lin_reg_scaled.score(x_test_scaled, y_test_multi)
print(f"归一化后多元线性回归 R² 分数: {score_scaled}")

输出：
归一化后多元线性回归 R² 分数: 0.5582591396048212

多项式回归

python 复制代码 
import numpy as np
import matplotlib.pyplot as plt
# 构造非线性数据
x = np.random.uniform(-4,2,size=(100))
y = 2*x**2 + 4*x + 3 + np.random.randn(100)
X = x.reshape(-1,1)
plt.scatter(x,y)
plt.show()
#线性回归
from sklearn.linear_model import LinearRegression
linear_regression = LinearRegression()
linear_regression.fit(X,y)
y_predict = linear_regression.predict(X)
plt.scatter(x,y)
plt.plot(x,y_predict,color='red')
plt.show()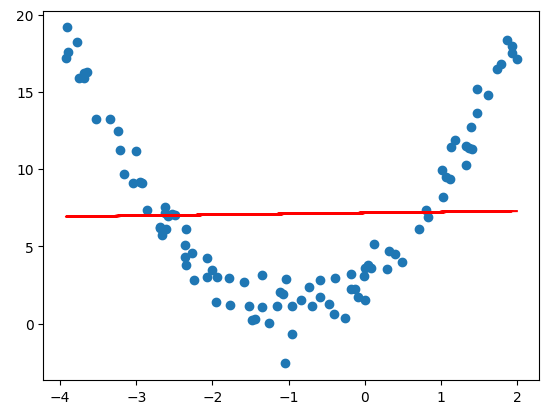
python 复制代码 
# 多项式回归
X[:5]
X_new = np.hstack([X,X**2])
X_new[:5]
linear_regression_new = LinearRegression()
linear_regression_new.fit(X_new,y)
y_predict_new = linear_regression_new.predict(X_new)
plt.scatter(x,y)
plt.plot(np.sort(x),y_predict_new[np.argsort(x)],color="red")
plt.show()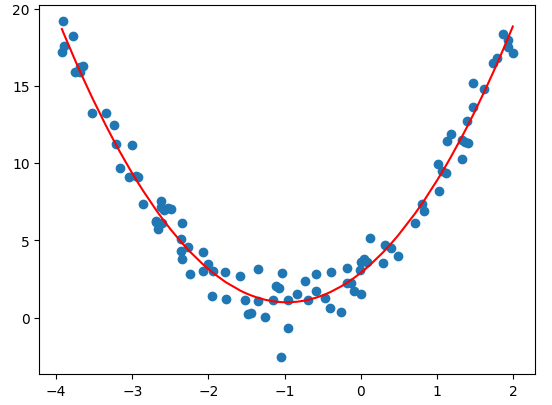
python 复制代码 
# 函数的截距
linear_regression_new.intercept_
# 特征值
linear_regression_new.coef_

输出：
np.float64(2.910763300495222)
array([3.93855269, 2.02866524])
python 复制代码 
# scikit-learn中的PolynomialFeatures
from sklearn.preprocessing import PolynomialFeatures
polynomial_features = PolynomialFeatures(degree=2)
X_poly = polynomial_features.fit_transform(X)
X_poly[:5]

输出：
array([[ 1.        , -2.62673044,  6.89971278],
       [ 1.        , -0.40289062,  0.16232085],
       [ 1.        , -2.35268823,  5.53514189],
       [ 1.        ,  1.00887873,  1.01783629],
       [ 1.        ,  1.8734883 ,  3.5099584 ]])

逻辑回归

叫着回归的名，做着分类的活

  1. 线性逻辑回归

逻辑函数（Logistic Function）：

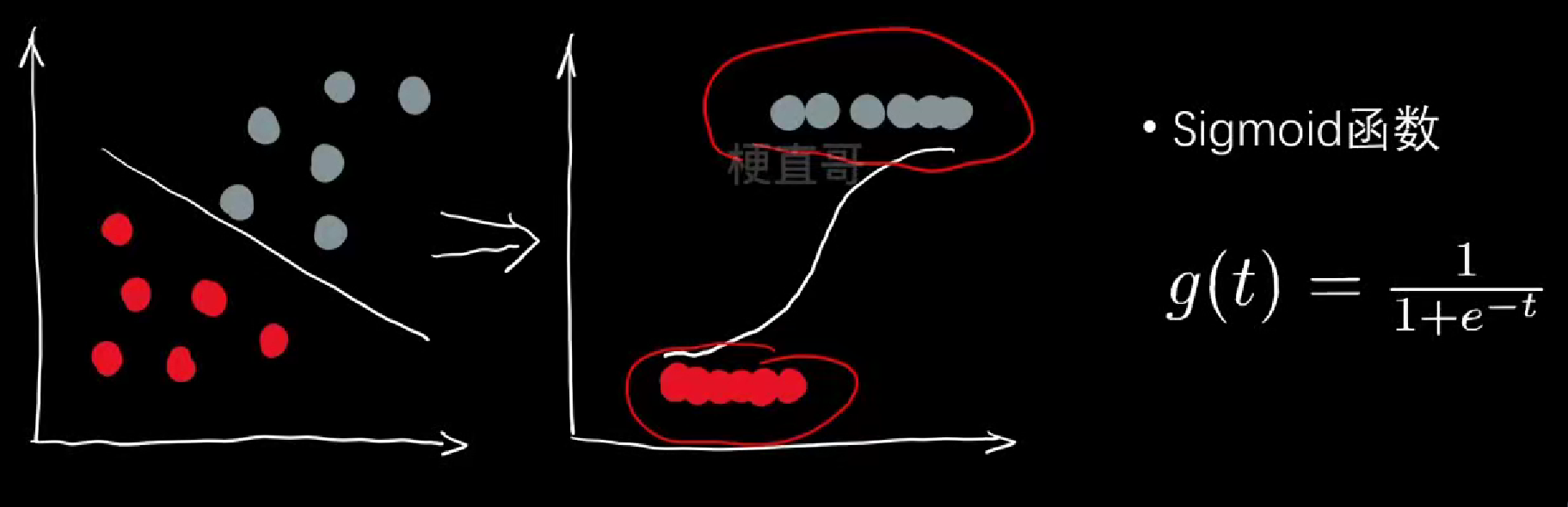
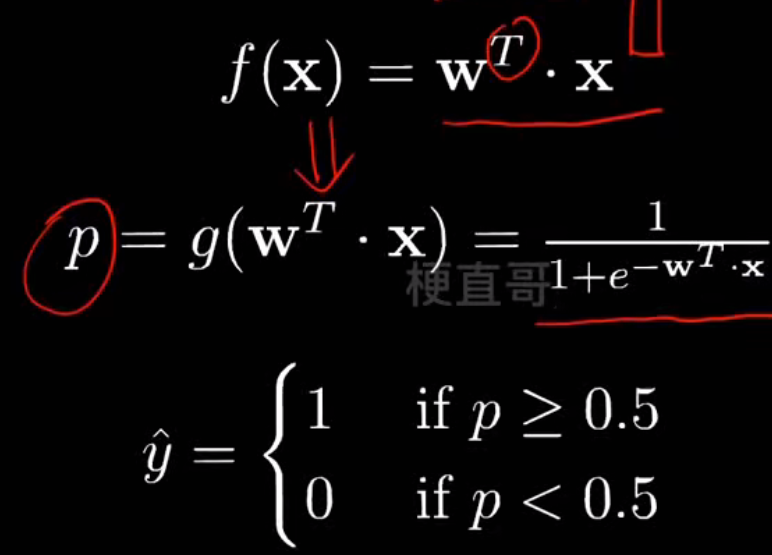
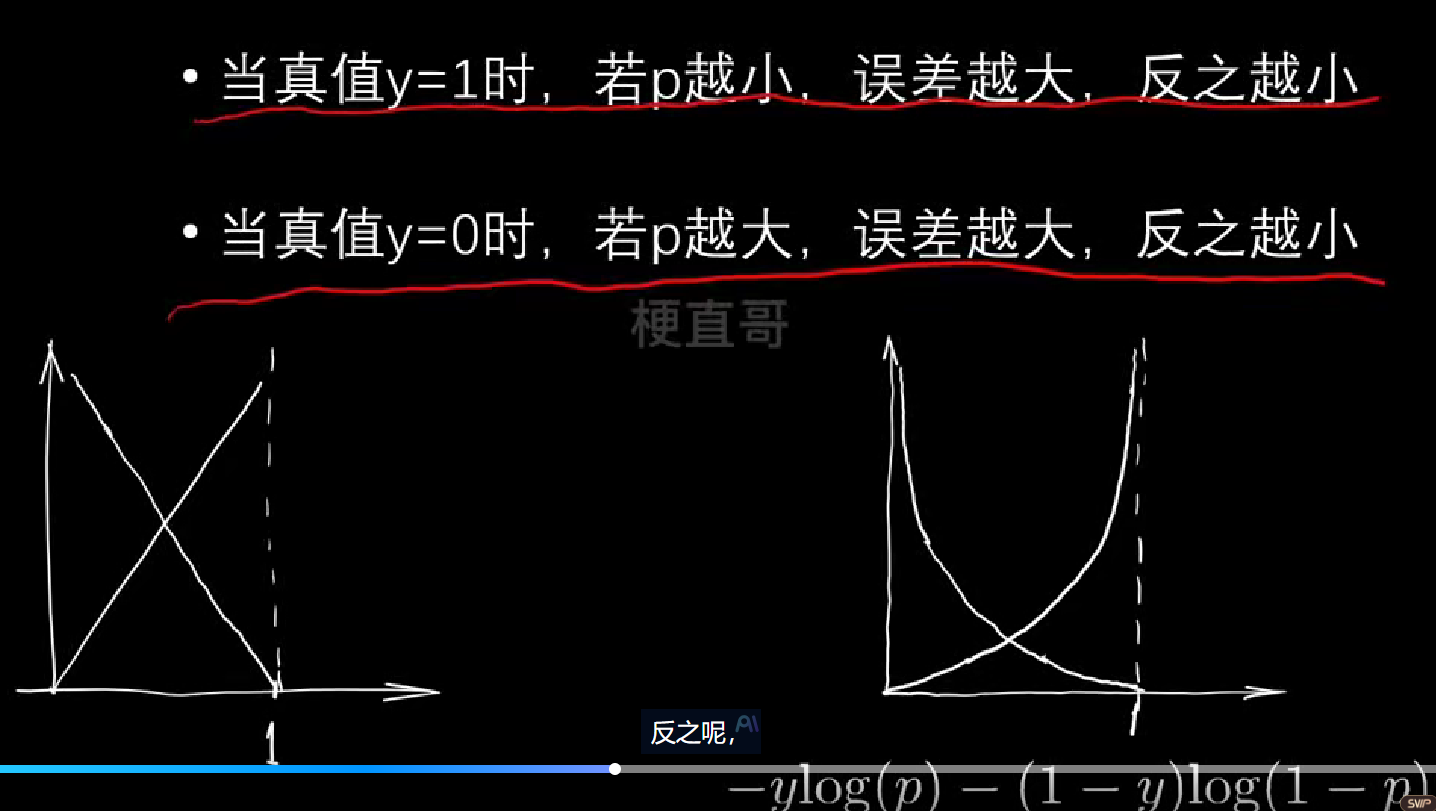
python 复制代码 
# 生成训练集
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification

x, y = make_classification(
    n_samples=200,
    n_features=2,
    n_redundant=0,
    n_classes=2,
    n_clusters_per_class=1,
    random_state=1024
)
x.shape, y.shape
x_train, x_test, y_train, y_test = train_test_split(x, y, train_size = 0.7, random_state = 233, stratify = y)
plt.scatter(x_train[:,0], x_train[:,1], c = y_train)
plt.show()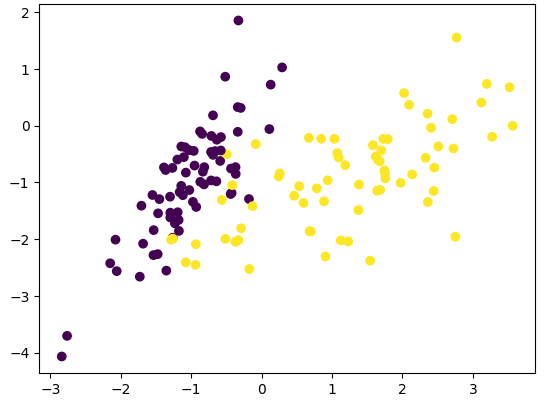
python 复制代码 
# sklearn中的逻辑回归
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression()
clf.fit(x_train, y_train)
clf.score(x_train, y_train)   #0.9357142857142857
clf.score(x_test, y_test)     #0.95
clf.predict(x_test)
输出：
array([1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1,
       0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1,
       0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0])
# 属于每个类别的概率
clf.predict_proba(x_test)
# 取概率最大的类别索引（即预测类别）
np.argmax(clf.predict_proba(x_test), axis = 1)
输出：
array([1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1,
       0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1,
       0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0])
python 复制代码 
# 超参数调优
# 用 网格搜索（GridSearchCV） 自动尝试多组超参数组合，找到让模型效果最好的那一组
from sklearn.model_selection import GridSearchCV
params = [{
    'penalty': ['l2', 'l1'],
    'C': [0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000],
    'solver': ['liblinear']
}, {
    'penalty': ['none'],
    'C': [0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000],
    'solver': ['lbfgs']
}, {
    'penalty': ['elasticnet'],
    'C': [0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000],
    'l1_ratio': [0, 0.25, 0.5, 0.75, 1],
    'solver': ['saga'],
    'max_iter': [200]
}]
grid = GridSearchCV(
    estimator=LogisticRegression(),
    param_grid=params,
    n_jobs=-1
)
grid.fit(x_train, y_train)
grid.best_score_   #np.float64(0.95)
grid.best_estimator_.score(x_test, y_test)  #0.9333333333333333
grid.best_params_
输出：
{'C': 1,
 'l1_ratio': 0.75,
 'max_iter': 200,
 'penalty': 'elasticnet',
 'solver': 'saga'}
  1. 多项式逻辑回归：

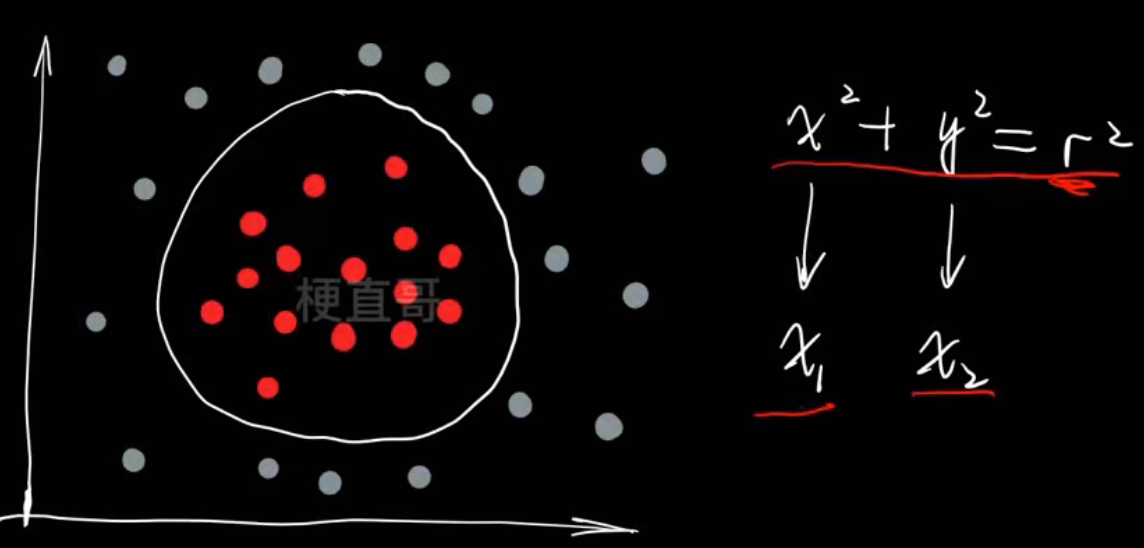
生成数据集

python 复制代码 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification
np.random.seed(0)
X = np.random.normal(0,1,size=(200,2))
y = np.array((X[:,0]**2)+(X[:,1]**2)<2, dtype='int')
y
输出：
array([0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0,
       1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1,
       0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1,
       1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1,
       1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0,
       1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1,
       0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0,
       0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1,
       0, 0])

x_train, x_test, y_train, y_test = train_test_split(X, y, train_size = 0.7, random_state = 233, stratify = y)
plt.scatter(x_train[:,0], x_train[:,1], c = y_train)
plt.show()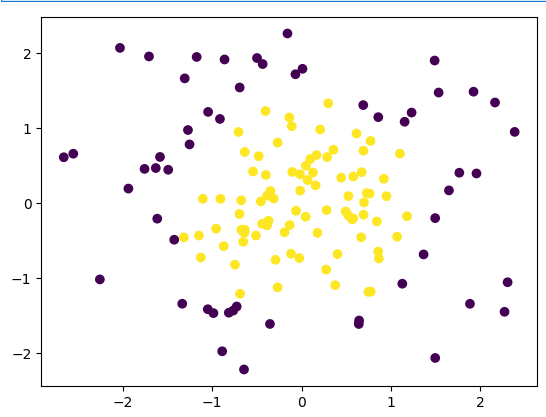

多项式逻辑回归代码实现：

python 复制代码 
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2)
poly.fit(x_train)
x2 = poly.transform(x_train)
x2t = poly.transform(x_test)
clf.fit(x2, y_train)
clf.score(x2, y_train)  # 1.0
clf.score(x2t, y_test)  # 0.9666666666666667

线性回归的模型评价

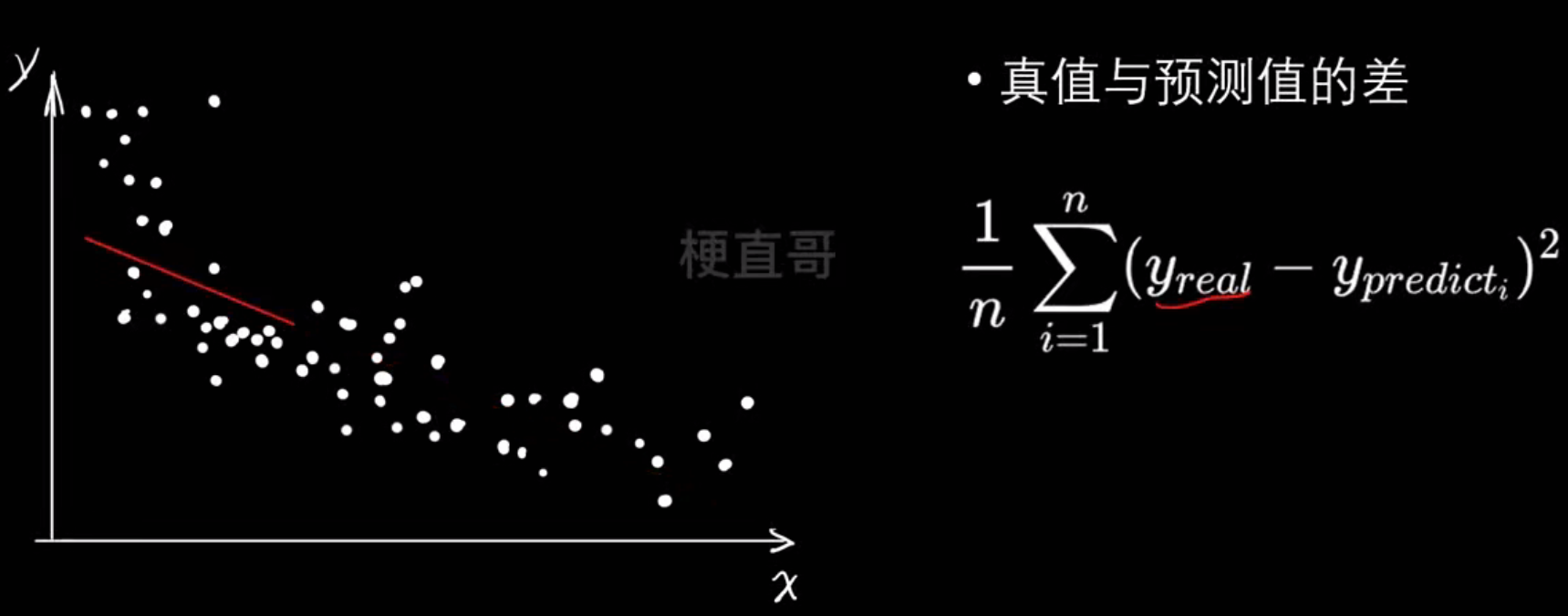
有误差怎么办？

python 复制代码 
# 加州房价预测模型（线性回归 + 模型评估 + 可视化）
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score

data = fetch_california_housing()
X = data.data
y = data.target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)

scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

model = LinearRegression()
model.fit(X_train, y_train)

y_pred = model.predict(X_test)

mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

print("===== 加州房价预测模型评价 =====")
print(f"均方误差 (MSE): {mse:.4f}")
print(f"均方根误差 (RMSE): {rmse:.4f}")
print(f"平均绝对误差 (MAE): {mae:.4f}")
print(f"决定系数 (R²): {r2:.4f}")

输出：
均方误差 (MSE): 0.5411
均方根误差 (RMSE): 0.7356
平均绝对误差 (MAE): 0.5297
决定系数 (R²): 0.5911
  1. 均方误差（MSE, Mean Squared Error）

特点：

  • 误差平方会放大大偏差样本的影响 → 对"极端错误"更敏感。
  • 单位是"平方单位"（在这里是房价平方，解释上不直观）。

解读结果：

MSE = 0.5411

→ 模型预测值与真实房价的平均平方偏差约为 0.54（单位约是"十万美元²"）。

  1. 均方根误差（RMSE, Root Mean Squared Error）

解读结果：

RMSE = 0.7356

→ 模型平均预测误差约为 0.73 个房价单位 （约 $73,000 左右）。

可理解为：模型的预测结果平均偏差在 ±7 万美元上下。

  1. 平均绝对误差（MAE, Mean Absolute Error）

解读结果：

MAE = 0.5297

→ 模型平均每个样本预测偏差约 0.53 个房价单位 （≈ $53,000）。

相当于：平均每套房预测误差大概五万美元上下。

  1. 决定系数（R², Coefficient of Determination）

解读结果：

R² = 0.5911

→ 模型能解释房价变化中 约 59% 的方差，剩下 41% 由未建模的因素（非线性关系、特征缺失等）决定。

指标 含义 理想情况 你的结果 说明
MSE 平方误差平均 越小越好 0.5411 整体误差适中
RMSE 与原单位一致的均方误差 越小越好 0.7356 平均预测误差约 $73,000
MAE 平均绝对误差 越小越好 0.5297 平均偏差约 $53,000
R² 拟合优度 越接近1越好 0.5911 模型解释力中等偏上

多分类策略

复杂问题简单化，把多分类问题转化为二分类问题：

  1. one vs one一对一-------- 每次对两个类别进行分类

如图有四组数据，每次拿出两个

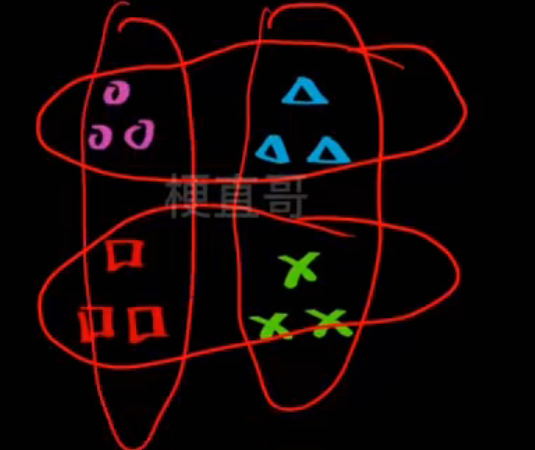
一共可以分为六组

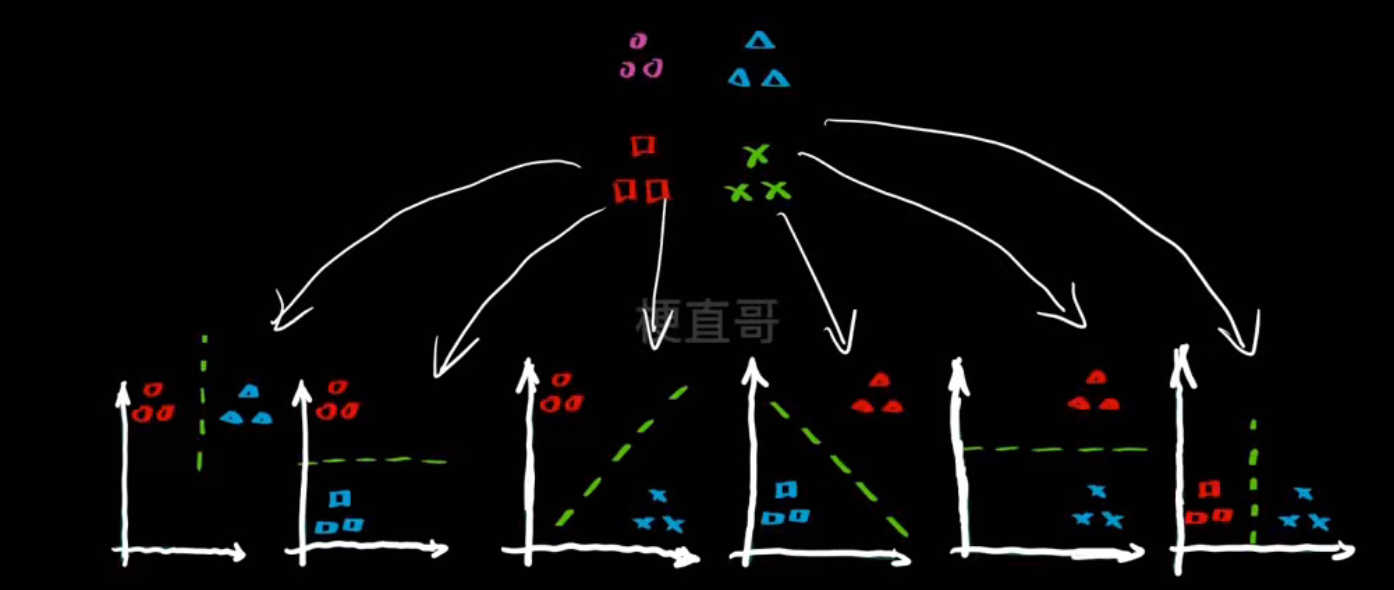
  1. one vs rest一对剩余------ 每次对一个类别 vs 其他所有类别
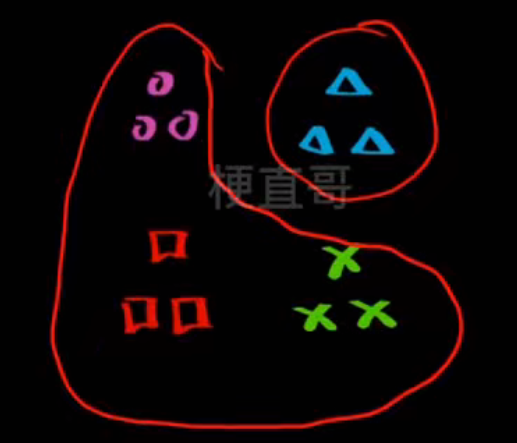
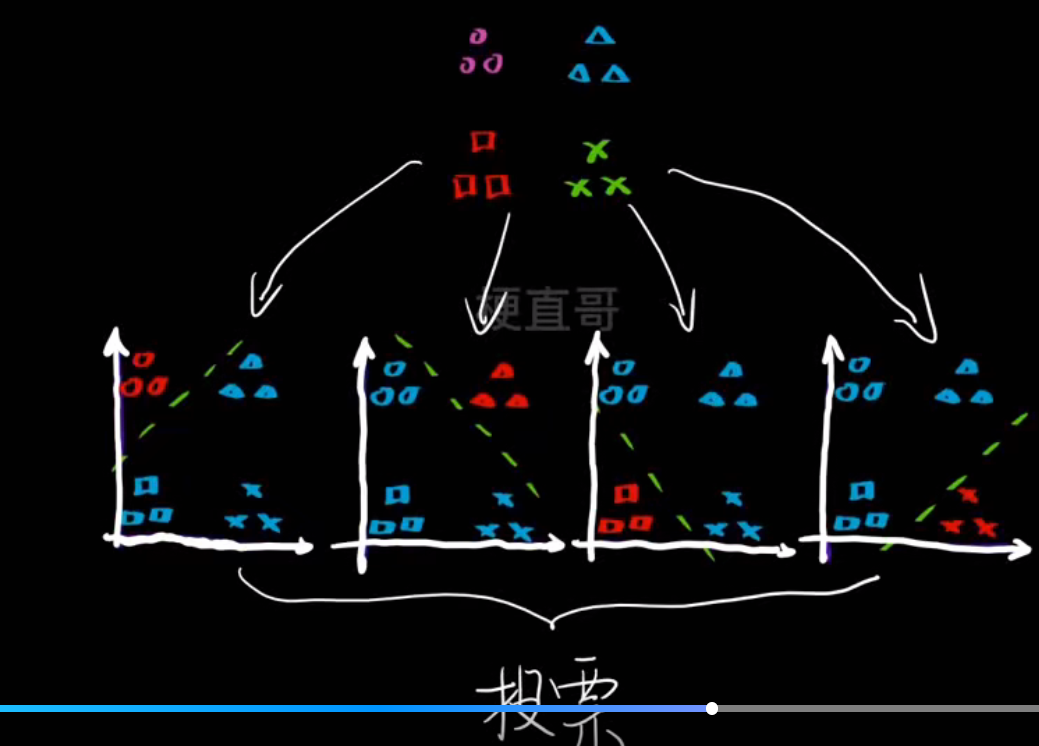
  1. 性能对比

生成数据集

python 复制代码 
from sklearn import datasets
iris = datasets.load_iris()
x = iris.data
y = iris.target
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=666)
plt.scatter(x_train[:,0], x_train[:,1], c=y_train)
plt.show()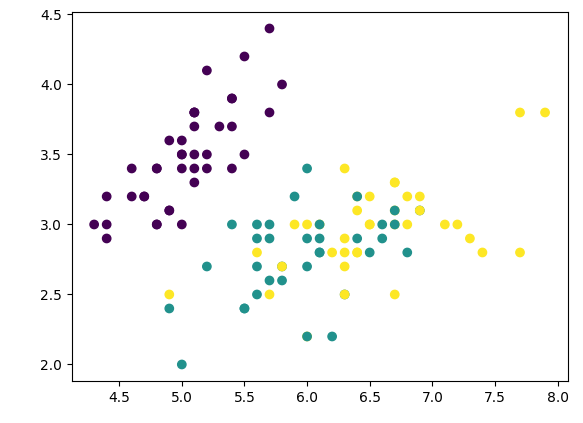
python 复制代码 
# 一对一
from sklearn.multiclass import OneVsOneClassifier

ovr = OneVsOneClassifier(clf)
ovr.fit(x_train,y_train)
ovr.score(x_test, y_test)  # 1.0

# 一对多
from sklearn.multiclass import OneVsRestClassifier

ovr = OneVsRestClassifier(clf)
ovr.fit(x_train,y_train)
ovr.score(x_test, y_test)  #0.9736842105263158

线性算法优缺点及使用条件

类别 线性回归 多项式回归 逻辑回归
数学表达式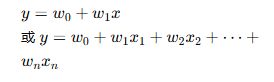
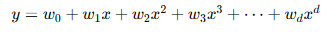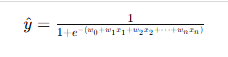模型类型 回归（预测连续值） 回归（预测连续值，非线性） 分类（预测0/1概率）
可视化示意 一条直线拟合数据 （线性趋势） 一条弯曲的平滑曲线 （可拟合非线性关系） 一条S形曲线（Sigmoid） （输出0~1概率）
优点 1. 模型简单、易理解 2. 建模和训练速度快 1. 能拟合非线性数据 2. 学习能力更强 3. 在合适阶数下表现优越 1. 模型清晰，参数解释性强 2. 输出有概率意义 3. 计算量小，可在线学习 4. 可处理过拟合（L1/L2正则）
缺点 1. 对异常值敏感 2. 无法表达复杂模式 3. 仅能拟合线性关系 1. 阶数选择不当易过拟合 2. 对异常值仍敏感 3. 特征数量急剧增加 1. 只能用于分类问题 2. 特征空间大时性能下降 3. 处理特征相关性较差
适用场景 数据趋势接近线性时，如房价~面积 变量间存在非线性关系，如温度~时间、销量价格曲线 二分类任务，如垃圾邮件识别、疾病预测、客户流失判断
核心思想 找一条直线，使预测值与真实值差距最小 用线性模型在高维空间近似非线性关系 使用 Sigmoid 将线性结果映射为概率，进行分类
输出形式 连续值（实数） 连续值（平滑曲线） 概率值（0~1）

3、核心概念精讲

机器学习干啥的：

四种语言的转换：

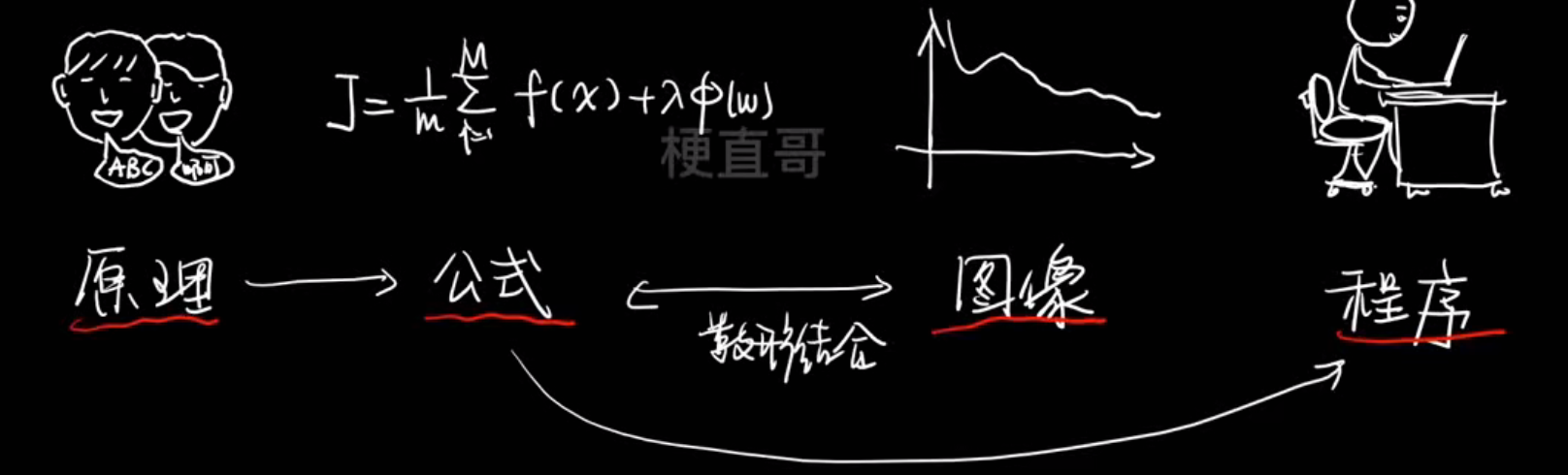
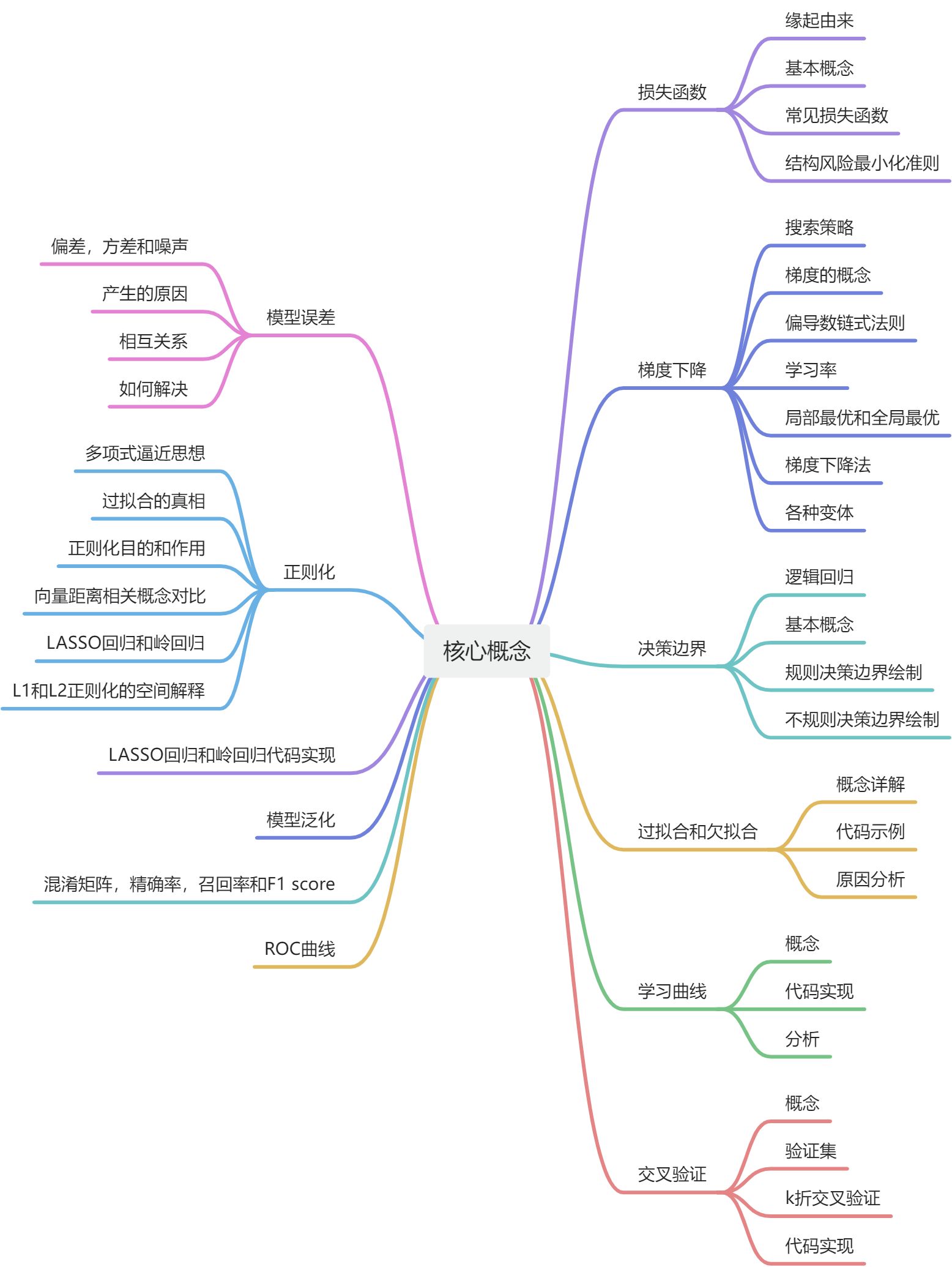
损失函数

缘由：

  • 机器学习的本质是在数据中找规律
  • 先假定带参数的模型
  • 数据投票打分的数学描述
  • Loss function/cost function

损失函数：针对不同情况下用不同标准来衡量样本和模型之间的损失

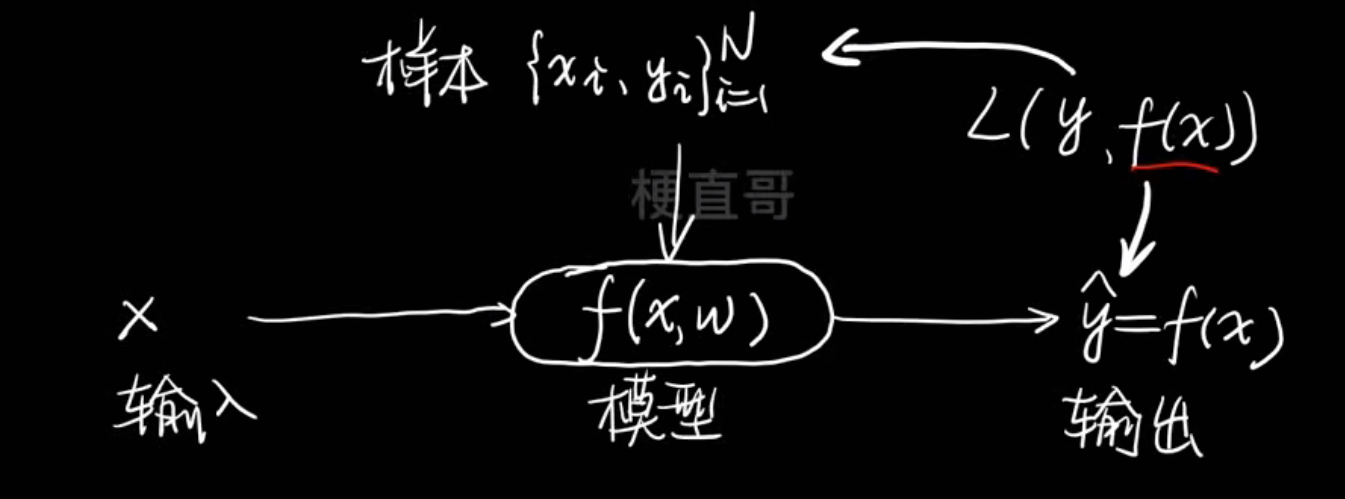
损失函数越小，说明效果越好

常见损失函数：

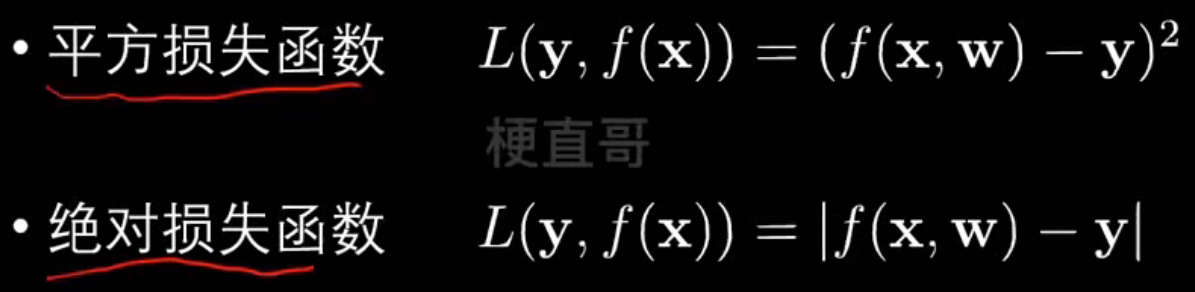
什么是熵？

  • 衡量混乱程度
  • 熵增定律

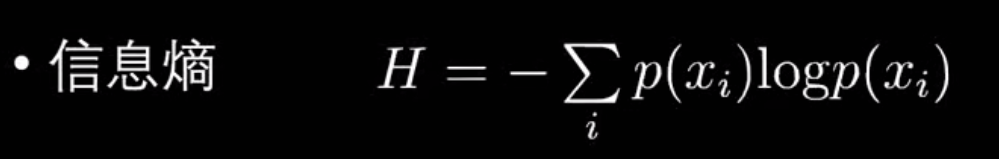
交叉熵直观解释：

交叉熵就是一个 衡量两个概率分布差异的指标，差距越大，交叉熵越大

其他损失函数

对比项 经验风险最小化 (ERM) 结构风险最小化 (SRM)
思想核心 让训练误差最小 让"训练误差 + 模型复杂度"总和最小
是否防过拟合 容易过拟合 可以抑制过拟合
数学形式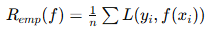
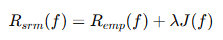典型算法 普通线性回归、KNN 岭回归、LASSO、SVM
惩罚项 无 有，如 (
理论基础 统计学习的经验逼近 Vapnik 的 VC 维理论（模型容量控制）

梯度下降

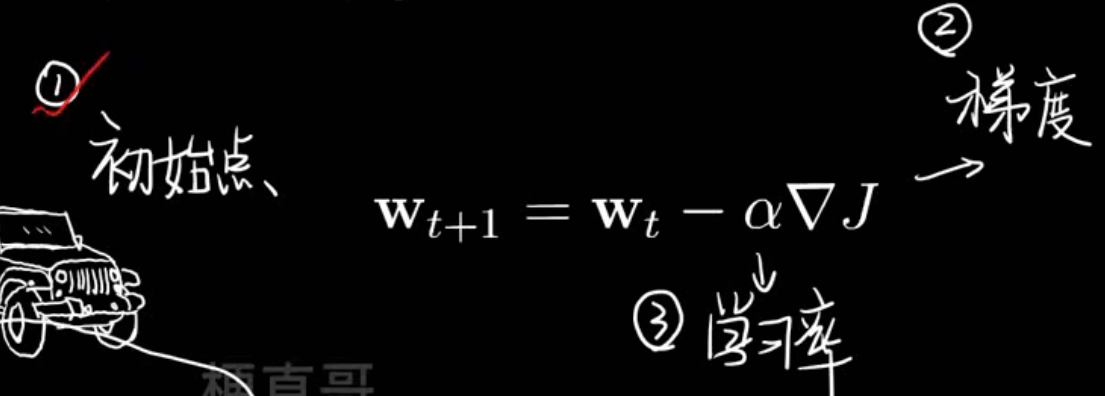
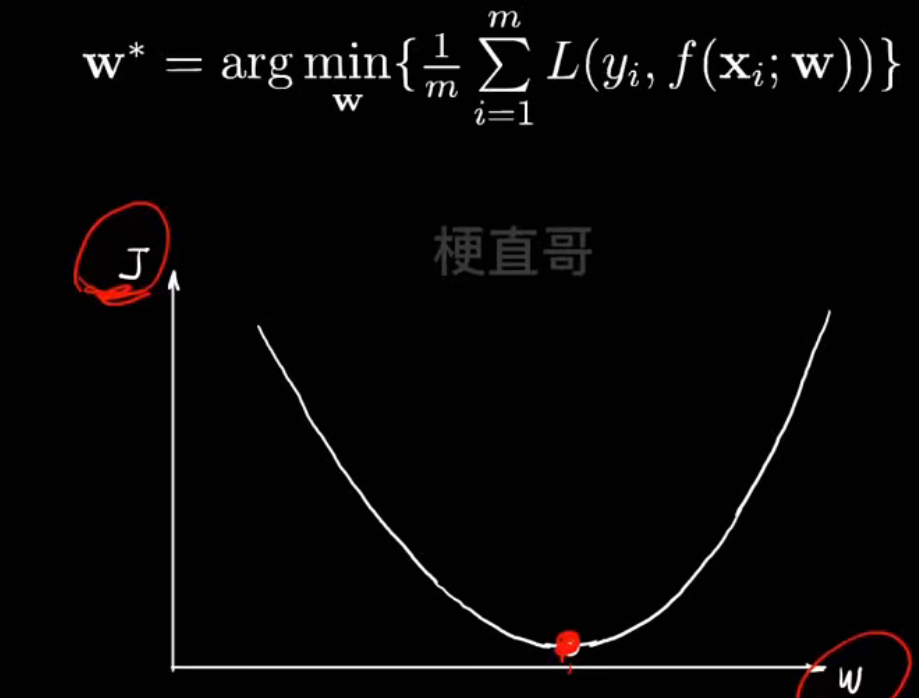
这是一种最优化算法，为了 找到一组参数 w,b，让损失函数 L的值最小

如图，显然最低点的时候损失最小

那么怎么找到这个最低点呢？

用搜索策略

这是最优化的核心

确定好搜索方向和搜索速度

梯度（Gradient）就是函数曲面陡度，偏导数是具体方向的陡度，梯度是所有方向偏导数向量和

学习率：

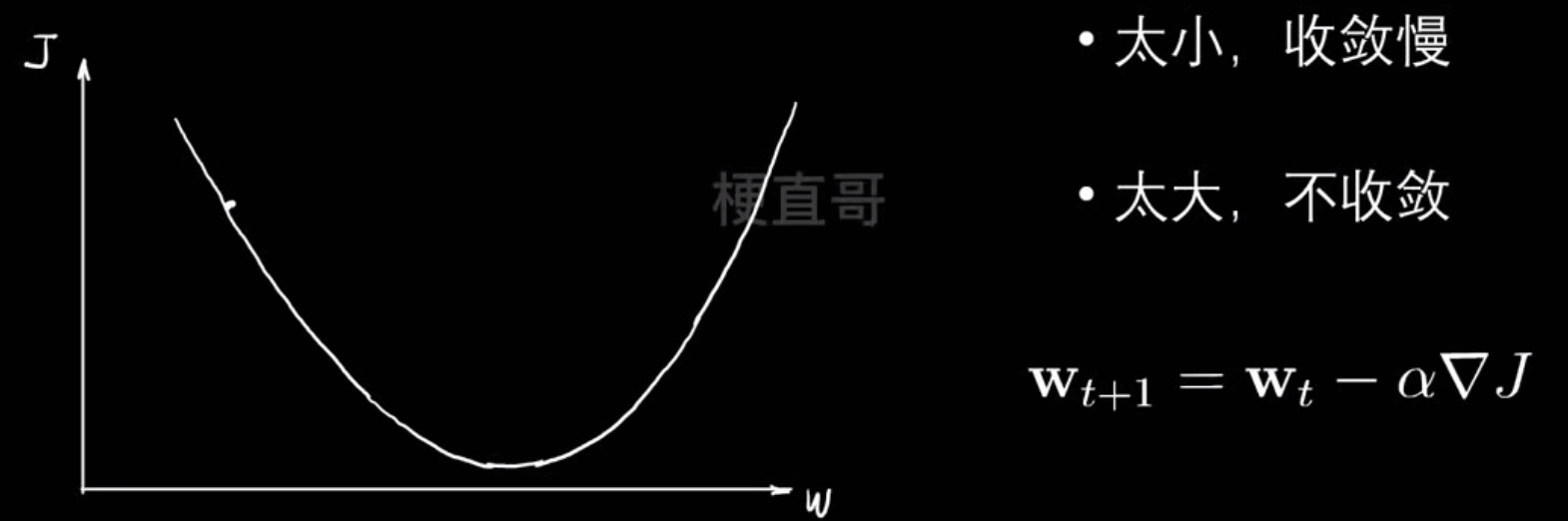
梯度下降过程中往往极值点不止一个，辨析局部最优和全局最优

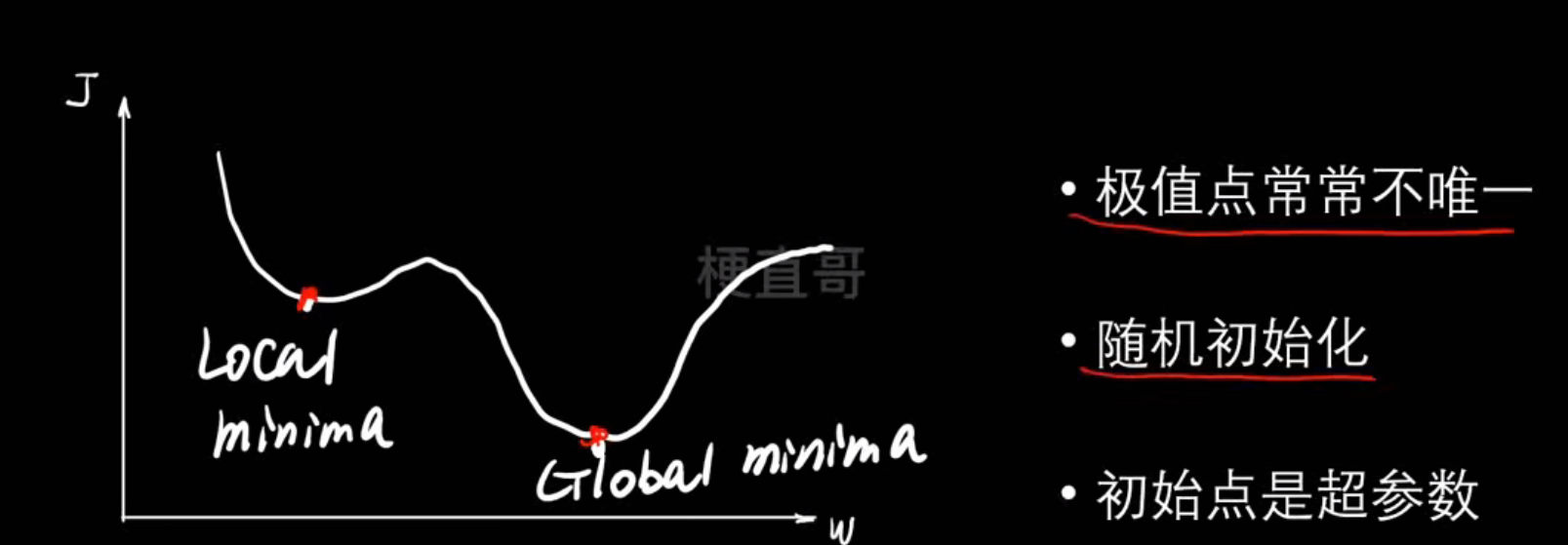
寻找最低点的过程中陷入局部最优，于是我们需要寻找更好的下山办法：

  • AdaGrad → 每个参数独立学习率
  • RMSProp → 防止学习率衰减过快
  • AdaDelta → 自动调节学习率
  • Adam → 综合优点，最常用

常见梯度下降算法：

方法 每次迭代样本量 优点 缺点 典型应用
批量梯度下降（BGD） 全部样本 收敛稳定、结果精确 计算量大、内存占用高 小数据集或离线训练
随机梯度下降（SGD） 1个样本 更新快、可跳出局部最优 收敛不稳定、震荡大 在线学习、流式数据
小批量梯度下降（Mini-Batch） 部分样本（如32~256） 稳定高效、支持并行 批量大小需调参 深度学习主流方法

决策边界

分类模型如何描绘决策边界

决策边界是模型将不同类别区分开的分界线（或曲面） 。换句话说，它定义了模型在输入空间中"判定类别"的临界位置。

不同算法的决策边界

模型类型 决策边界形状 举例说明
线性模型（如 Logistic Regression, Linear SVM） 直线（二维）或超平面（高维） 用线性方程 ( w^T x + b = 0 ) 划分空间
非线性模型（如 Kernel SVM, 决策树, 神经网络） 曲线或复杂曲面 可以弯曲、折叠甚至形成多个区域
k近邻（KNN） 不规则边界 取决于样本分布，边界会非常"碎"
神经网络 随层数增加可学到非常复杂的非线性边界 CNN、MLP 等深层模型能逼近任意形状的边界

举个例子：

规则边界绘制：

python 复制代码 
# 线性逻辑回归决策边界
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression

x,y=make_classification(
    n_samples=200,
    n_features=2,
    n_redundant=0,
    n_classes=2,
    n_clusters_per_class=1,
    random_state=1024
)
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.7,random_state=24)
clf=LogisticRegression()
clf.fit(x_train,y_train)
clf.score(x_train,y_train) #0.9333333333333333
plt.scatter(x_train[:,0],x_train[:,1],c=y_train)
plt.show()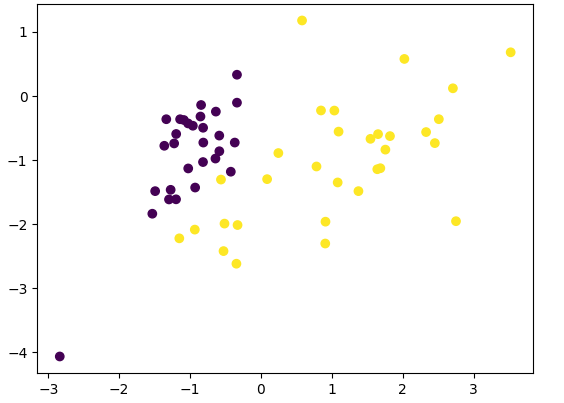
python 复制代码 
clf.coef_ # # 权重 w,array([[ 2.51671784, -1.3052424 ]])
clf.intercept_ # 截距 b,array([-0.61049327])
x1=np.linspace(-4,4,1000)
x2=(-clf.coef_[0][0]*x1-clf.intercept_)/clf.coef_[0][1]
plt.scatter(x_train[:,0],x_train[:,1],c=y_train)
# 决策边界
plt.scatter(x1,x2)
plt.show()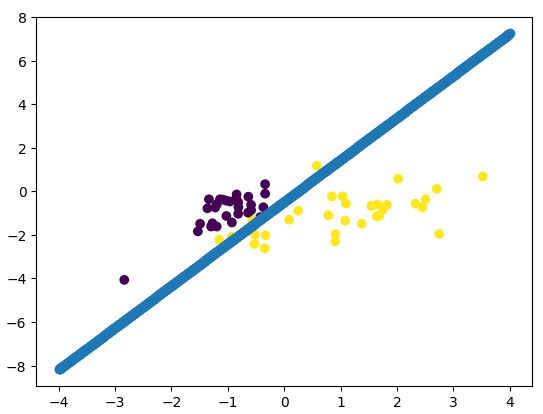
python 复制代码 
# 决策边界绘制函数
def decision_boundary_plot(X, y, clf):
    axis_x1_min, axis_x1_max = X[:,0].min() - 1, X[:,0].max() + 1
    axis_x2_min, axis_x2_max = X[:,1].min() - 1, X[:,1].max() + 1
    
    x1, x2 = np.meshgrid( np.arange(axis_x1_min,axis_x1_max, 0.01) , np.arange(axis_x2_min,axis_x2_max, 0.01))
    z = clf.predict(np.c_[x1.ravel(),x2.ravel()])
    z = z.reshape(x1.shape)
    
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#F5B9EF','#BBFFBB','#F9F9CB'])

    plt.contourf(x1, x2, z, cmap=custom_cmap)
    plt.scatter(X[:,0], X[:,1], c=y)
    plt.show()

decision_boundary_plot(x,y,clf)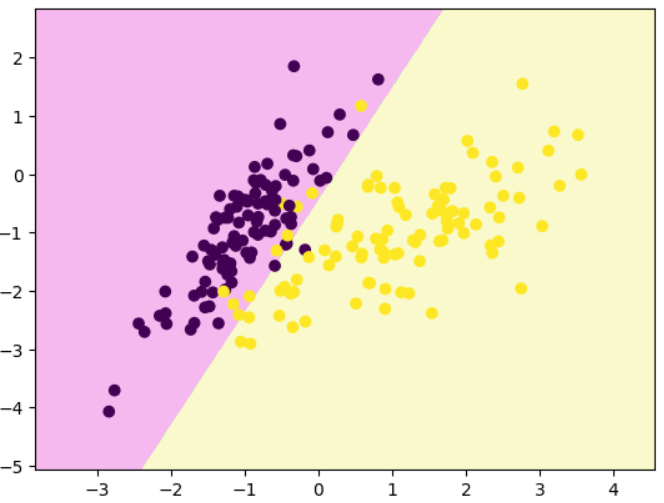

不规则边界绘制：

python 复制代码 
# 三分类
from sklearn import datasets
iris=datasets.load_iris()
x=iris.data[:,:2]
y=iris.target
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)
plt.scatter(x_train[:,0],x_train[:,1],c=y_train)
plt.show()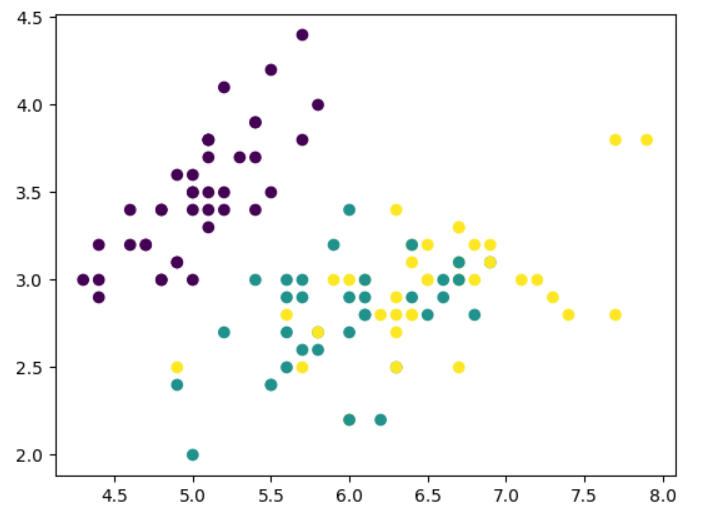
python 复制代码 
# 三分类的决策边界
clf.fit(x_train,y_train)
clf.score(x_test,y_test)   #0.7894736842105263
decision_boundary_plot(x,y,clf)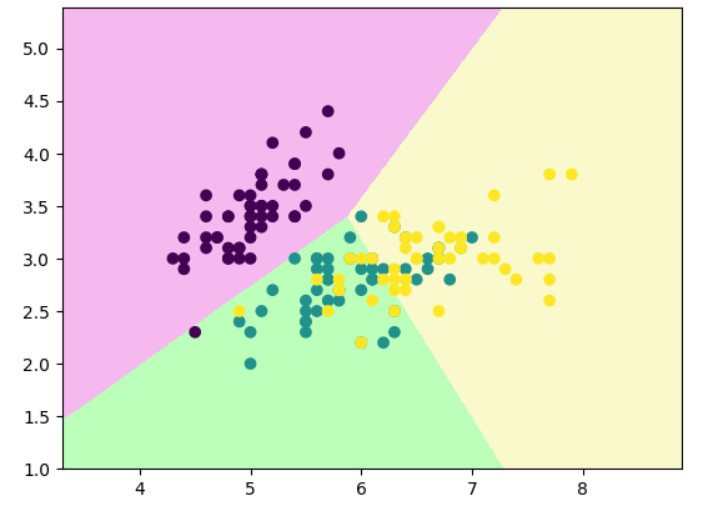
python 复制代码 
# 多项式逻辑回归
np.random.seed(0)
x = np.random.normal(0, 1, size=(200, 2))
y = np.array((x[:,0]**2+x[:,1]**2)<2, dtype='int')
x_train, x_test, y_train, y_test = train_test_split(x, y, train_size = 0.7, random_state = 233, stratify = y)
plt.scatter(x_train[:,0], x_train[:,1], c = y_train)
plt.show()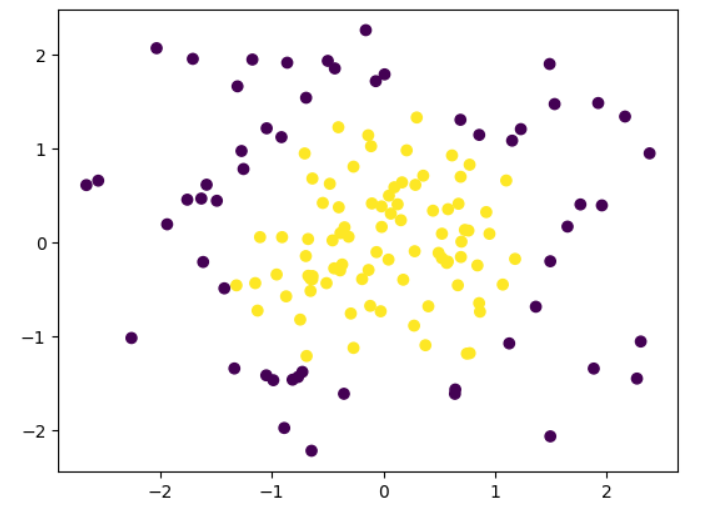
python 复制代码 
# 多项式逻辑回归的决策边界
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression

clf_pipe=Pipeline([
    ('poly',PolynomialFeatures(degree=2)),
     ('std_scaler',StandardScaler()),
     ('log_reg',LogisticRegression())
])
clf_pipe.fit(x_train,y_train)
decision_boundary_plot(x,y,clf_pipe)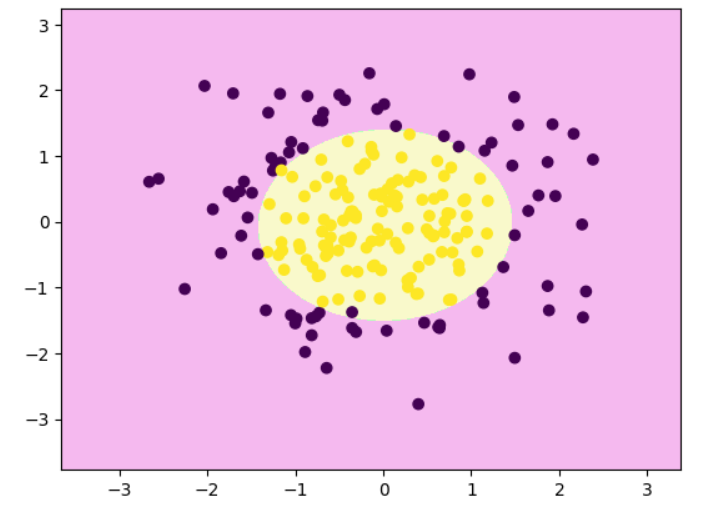

过拟合和欠拟合

python 复制代码 
# 数据集
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(233)
x=np.random.uniform(-4,2,size=(100))
y=x**2+4*x+3+2*np.random.randn(100)
X=x.reshape(-1,1)

plt.scatter(x,y)
plt.show()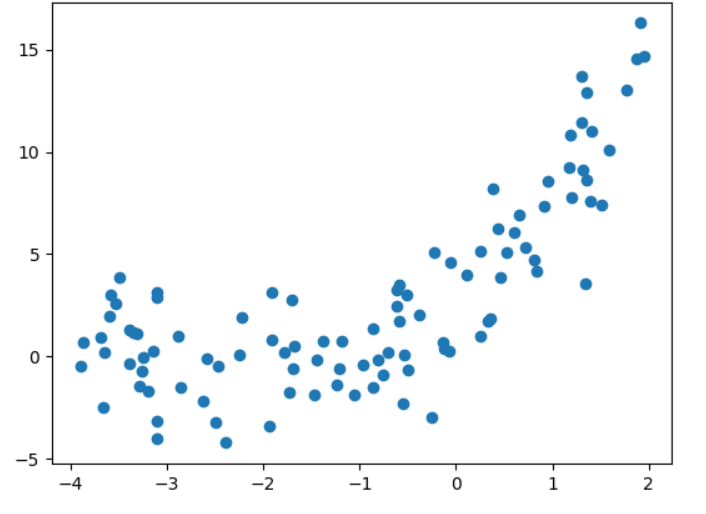
python 复制代码 
# 欠拟合
from sklearn.linear_model import LinearRegression
linear_regression=LinearRegression()
linear_regression.fit(X,y)
y_predict=linear_regression.predict(X)
plt.scatter(x,y)
plt.plot(x,y_predict,color='red')
plt.show()

linear_regression.score(X,y)  #0.5273556058762796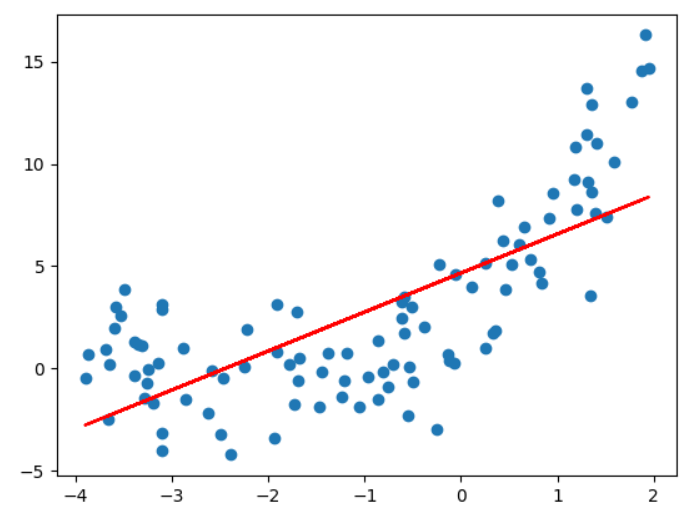
python 复制代码 
# 过拟合
from sklearn.preprocessing import PolynomialFeatures
polynomial_features=PolynomialFeatures(degree=2)
X_poly=polynomial_features.fit_transform(X)

linear_regression=LinearRegression()
linear_regression.fit(X_poly,y)

y_predict=linear_regression.predict(X_poly)

plt.scatter(x,y,s=10)
plt.plot(np.sort(x),y_predict[np.argsort(x)],color='red')
plt.show()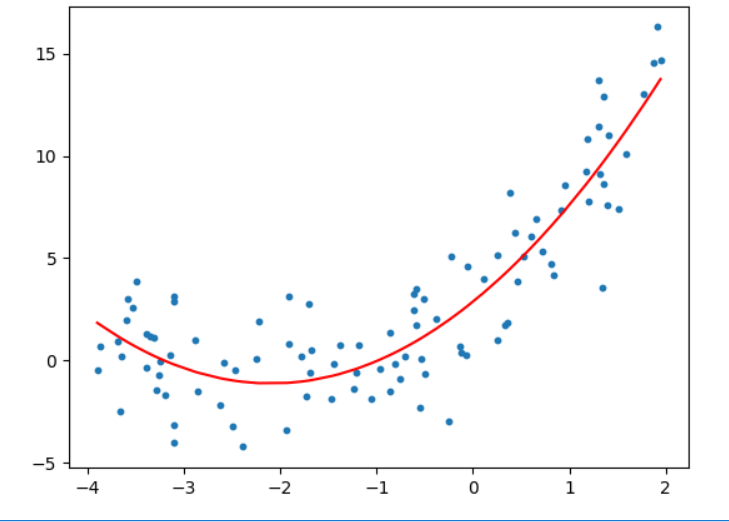
python 复制代码 
# 多项式回归另一种方法
X_new=np.linspace(-5,3,200).reshape(-1,1)
X_new_poly=polynomial_features.fit_transform(X_new)
y_predict=linear_regression.predict(X_new_poly)

plt.scatter(x,y,s=10)
plt.plot(X_new,y_predict,color='red')
plt.show()

print("Degree:",2,"Score:",linear_regression.score(X_poly,y))  #Degree: 2 Score: 0.7961121480231473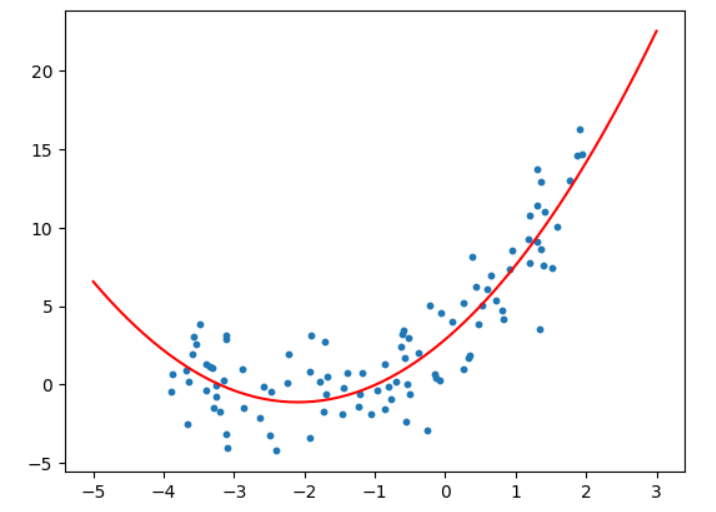
python 复制代码 
# 绘制不同degree效果
degrees=[2,5,10,15,20,24]
for i, degree in enumerate(degrees):
    polynomial_features = PolynomialFeatures(degree = degree)
    X_poly = polynomial_features.fit_transform(X)
    
    linear_regression = LinearRegression()
    linear_regression.fit(X_poly, y)
    
    X_new = np.linspace(-5, 3, 200).reshape(-1, 1)
    X_new_poly = polynomial_features.fit_transform(X_new)
    y_predict = linear_regression.predict(X_new_poly)
    
    plt.subplot(2, 3, i + 1)
    plt.title("Degree: {0}".format(degree))
    plt.scatter(x, y, s = 10)
    plt.ylim(-5, 25)
    plt.plot(X_new, y_predict, color = 'red')
    
    print("Degree:", degree, "Score:", linear_regression.score(X_poly, y))
    
plt.show()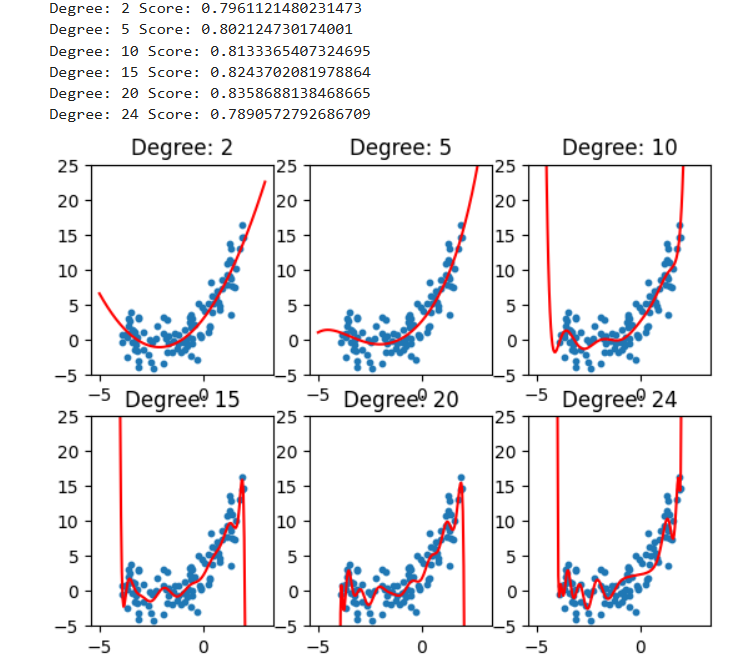

学习曲线

过拟合老要画曲线太麻烦了，我们通过学习曲线去评判拟合效果更简单

学习曲线就是：随着训练数据量增加，模型性能（误差或准确率）的变化曲线

什么是学习曲线？

它通常包含两条曲线：

  • 训练集曲线：模型在训练数据上的表现；
  • 验证集/测试集曲线：模型在新数据上的表现
情况 特征 含义
欠拟合（Underfitting） 训练误差高，测试误差也高，且两者都几乎不下降 模型太简单，学不到规律
过拟合（Overfitting） 训练误差很低，但测试误差高，两条曲线差距大 模型太复杂，记住了训练数据
拟合良好 两条曲线都低，并且趋于接近 模型复杂度合适、泛化好
python 复制代码 
# 数据集
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(233)
x=np.random.uniform(-4,2,size=(100))
y=x**2+4*x+3+2*np.random.randn(100)
X=x.reshape(-1,1)

plt.scatter(x,y)
plt.show()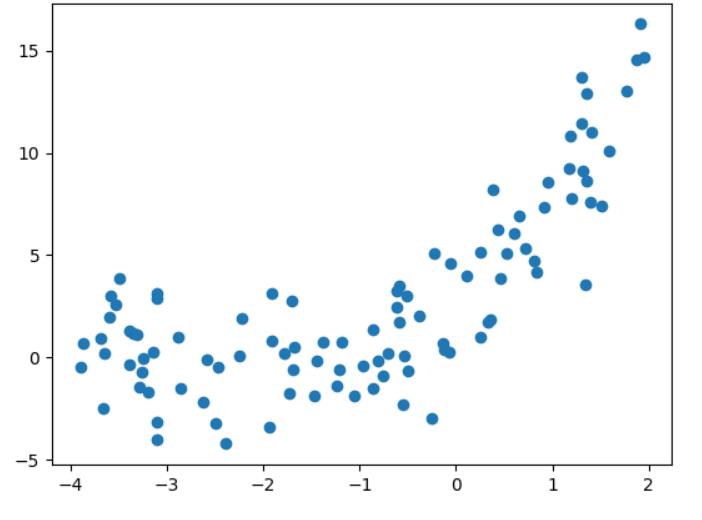
python 复制代码 
# 线性回归和多项式回归
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures

plt.rcParams["figure.figsize"] = (12, 8)

degrees = [1, 2, 5, 20]
for i, degree in enumerate(degrees):
    polynomial_features = PolynomialFeatures(degree = degree)
    X_poly = polynomial_features.fit_transform(X)

    linear_regression = LinearRegression()
    linear_regression.fit(X_poly, y)

    X_new = np.linspace(-5, 3, 200).reshape(-1, 1)
    X_new_poly = polynomial_features.fit_transform(X_new)
    y_predict = linear_regression.predict(X_new_poly)
    
    plt.subplot(2, 2, i + 1)
    plt.title("Degree: {0}".format(degree))
    plt.scatter(x, y, s = 10)
    plt.ylim(-5, 25)
    plt.plot(X_new, y_predict, color = "red")

    print("Degree:", degree, "Score:", linear_regression.score(X_poly, y))

plt.show()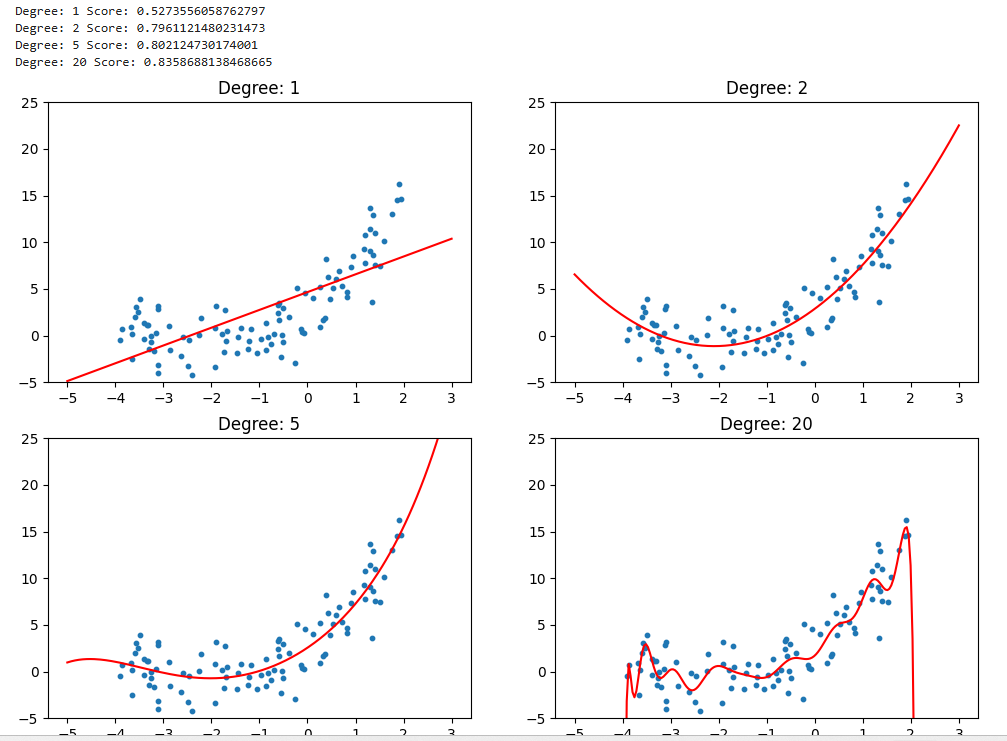
python 复制代码 
# 划分数据集
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,train_size=0.7,random_state=233)

x_train.shape,x_test.shape,y_train.shape,y_test.shape

输出：
((70,), (30,), (70,), (30,))
python 复制代码 
# 学习曲线
from sklearn.metrics import mean_squared_error

plt.rcParams["figure.figsize"] = (12, 8)

degrees = [1, 2, 5, 20]
for i, degree in enumerate(degrees):
    polynomial_features = PolynomialFeatures(degree = degree)
    
    X_poly_train = polynomial_features.fit_transform(x_train.reshape(-1, 1))
    X_poly_test = polynomial_features.fit_transform(x_test.reshape(-1, 1))
    
    train_error, test_error = [], []
    for k in range(len(x_train)):
        linear_regression = LinearRegression()
        linear_regression.fit(X_poly_train[:k + 1], y_train[:k + 1])

        y_train_pred = linear_regression.predict(X_poly_train[:k + 1])
        train_error.append(mean_squared_error(y_train[:k + 1], y_train_pred))

        y_test_pred = linear_regression.predict(X_poly_test)
        test_error.append(mean_squared_error(y_test, y_test_pred))
    
    plt.subplot(2, 2, i + 1)
    plt.title("Degree: {0}".format(degree))
    plt.ylim(-5, 50)
    plt.plot([k + 1 for k in range(len(x_train))], train_error, color = "red", label = 'train')
    plt.plot([k + 1 for k in range(len(x_train))], test_error, color = "blue", label = 'test')
    plt.legend()

plt.show()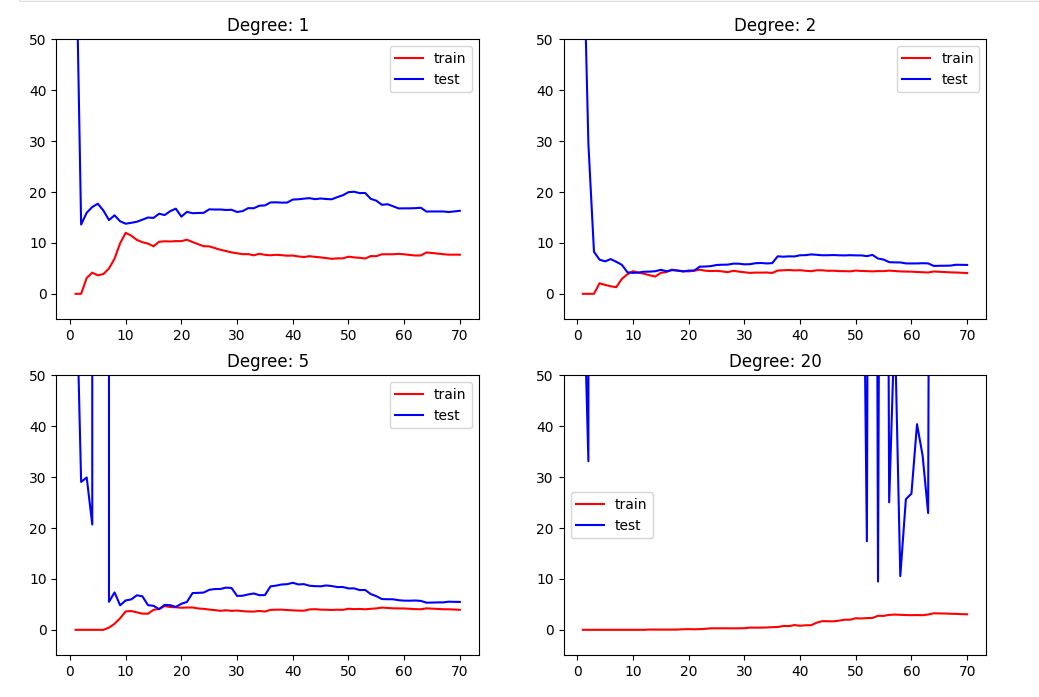
python 复制代码 
from sklearn.metrics import mean_squared_error

plt.rcParams["figure.figsize"] = (12, 8)

degrees = [1, 2, 5, 20]
for i, degree in enumerate(degrees):
    polynomial_features = PolynomialFeatures(degree = degree)
    
    X_poly_train = polynomial_features.fit_transform(x_train.reshape(-1, 1))
    X_poly_test = polynomial_features.fit_transform(x_test.reshape(-1, 1))
    
    train_error, test_error = [], []
    for k in range(1, len(x_train)):
        linear_regression = LinearRegression()
        linear_regression.fit(X_poly_train[:k + 1], y_train[:k + 1])

        train_error.append(linear_regression.score(X_poly_train[:k + 1], y_train[:k + 1]))
        test_error.append(linear_regression.score(X_poly_test, y_test))
    
    plt.subplot(2, 2, i + 1)
    plt.title("Degree: {0}".format(degree))
    plt.ylim(-1, 1)
    plt.plot([k + 1 for k in range(1, len(x_train))], train_error, color = "red", label = 'train')
    plt.plot([k + 1 for k in range(1, len(x_train))], test_error, color = "blue", label = 'test')
    plt.legend()

plt.show()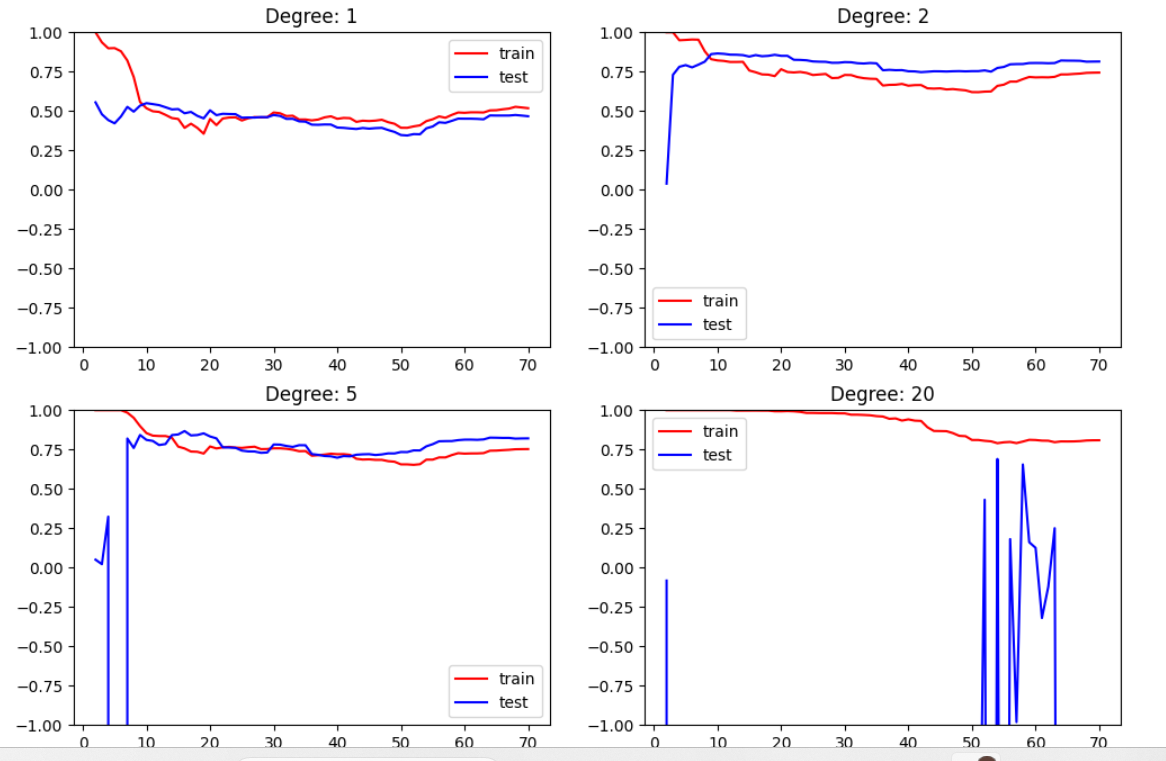
指标 含义 越什么越好 单位
MSE（Mean Squared Error） 预测值与真实值之间的平均平方差 越小越好 与原始数据单位的平方一致
R²（Coefficient of Determination） 模型能解释数据方差的比例（相对衡量） 越大越好（上限1） 无单位、相对指标
比较维度 第一版代码（用 mean_squared_error） 第二版代码（用 model.score()）
性能指标 使用 均方误差（MSE） 作为误差度量 使用 R² 决定系数 作为性能指标
纵轴含义 "误差" 越低越好（下越好） "拟合度" 越高越好（上越好）
显示方向 y轴是误差，越靠近 0 越优 y轴是 R²，越靠近 1 越优
曲线趋势 下降曲线：随着样本增加误差下降 上升曲线：随着样本增加R²上升
用途偏向 直观展示"误差下降趋势" 强调"模型解释能力提升"
易于发现的问题 过拟合/欠拟合更直观（看误差间距） 模型好坏更直观（看R²靠近1）
底层计算 每次调用 mean_squared_error() 每次调用 LinearRegression().score()
数值取值范围 MSE ≥ 0，无上限 R² ∈ (-∞, 1]
方向一致性 误差 ↓ → 模型更好 R² ↑ → 模型更好

交叉验证

验证集：

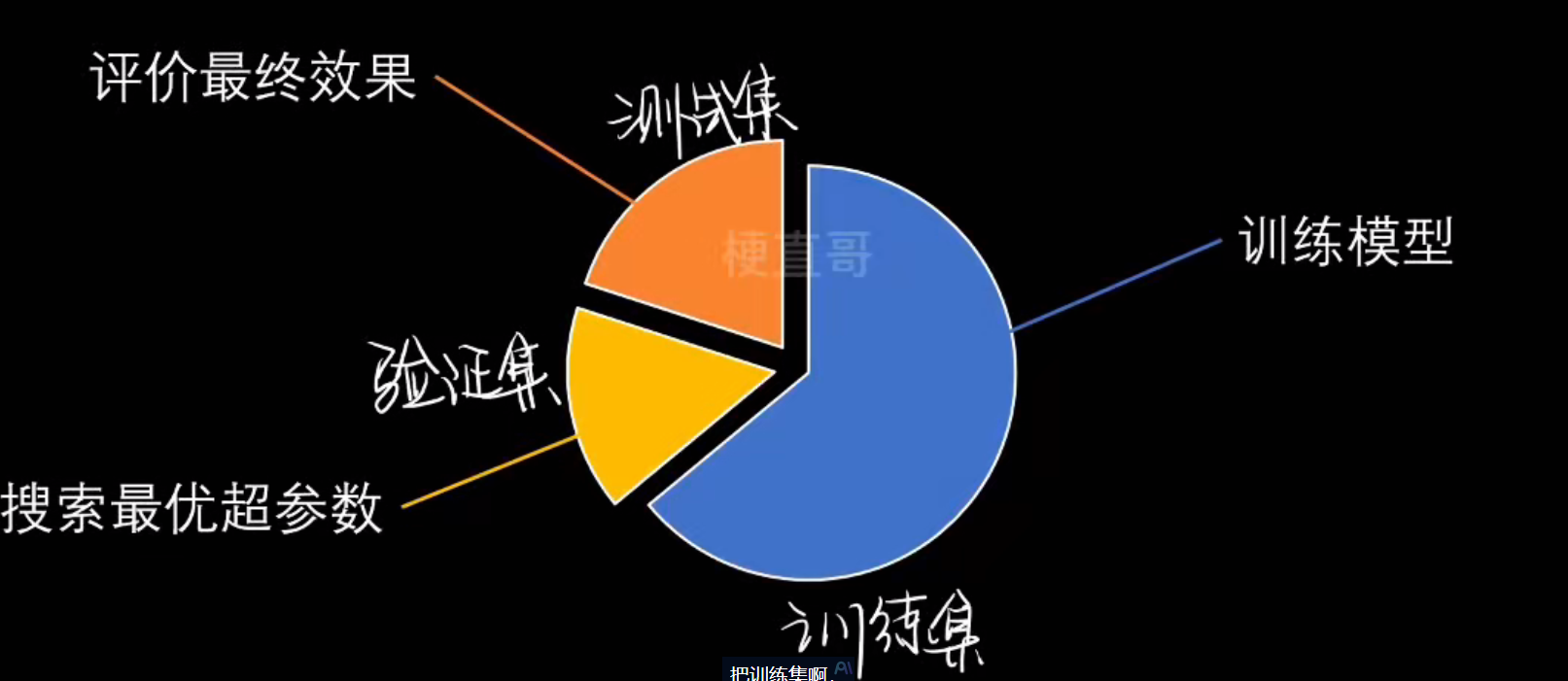
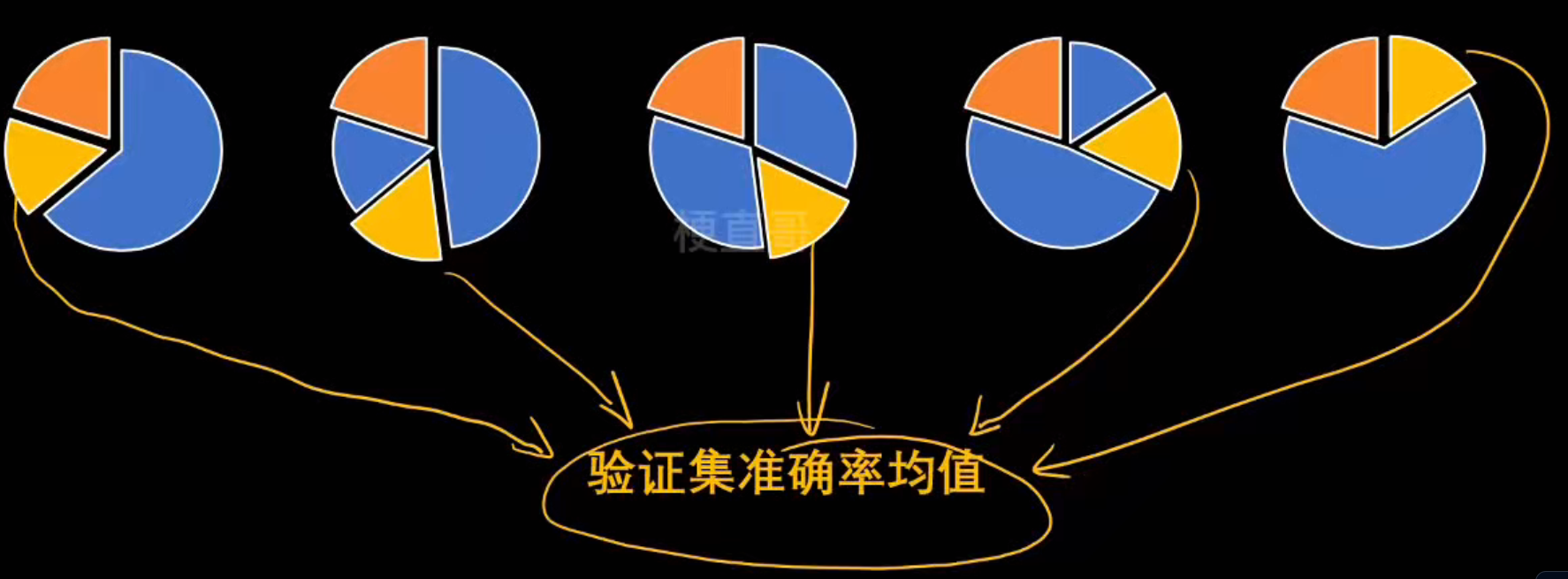
k-fold交叉验证：

python 复制代码 
┌──────────────────────────────┐
│  GridSearchCV 工作流程       │
│                              │
│  for 每一组超参:             │
│     for 每一折CV:            │
│         拆分训练/验证数据    │
│         训练模型 → 得分      │
│     平均折内得分             │
│  取平均分最高的超参组合       │
└──────────────────────────────┘

代码实现：

python 复制代码 
# 数据集
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris

iris = load_iris()
x = iris.data
y = iris.target

x_train, x_test, y_train, y_test = train_test_split(x, y, train_size = 0.7, random_state = 233, stratify = y)
x_train.shape, x_test.shape, y_train.shape, y_test.shape

输出：
((105, 4), (45, 4), (105,), (45,))
python 复制代码 
from sklearn.model_selection import cross_val_score
from sklearn.neighbors import KNeighborsClassifier

neigh = KNeighborsClassifier()、
# 把训练集 x_train, y_train 分成 5 份（cv=5），
# 用 5 折交叉验证（5-Fold Cross Validation）评估模型性能。
cv_scores = cross_val_score(neigh, x_train, y_train, cv = 5)
print(cv_scores)

输出：
[0.95238095 1.         0.95238095 0.85714286 1.        ]
轮次 训练集 验证集
第1次 折2~5 折1
第2次 折1,3,4,5 折2
第3次 折1,2,4,5 折3
第4次 折1,2,3,5 折4
第5次 折1,2,3,4 折5

每次：

  1. 模型用 4 份数据训练；
  2. 用剩下 1 份验证；
  3. 记录这次验证的准确率。

最后得到 5 个分数。

python 复制代码 
best_score = -1
best_n = -1
best_weight = ''
best_p = -1
best_cv_scores = None
for n in range(1, 20):
    for weight in ['uniform', 'distance']:
        for p in range(1, 7):
            neigh = KNeighborsClassifier(
                n_neighbors = n,
                weights = weight,
                p = p
            )
            cv_scores = cross_val_score(neigh, x_train, y_train, cv = 5)
            score = np.mean(cv_scores)
            if score > best_score:
                best_score = score
                best_n = n
                best_weight = weight
                best_p = p
                best_cv_scores = cv_scores

print("n_neighbors:", best_n)
print("weights:", best_weight)
print("p:", best_p)
print("score:", best_score)
print("best_cv_scores:", best_cv_scores)

输出：
n_neighbors: 9
weights: uniform
p: 2
score: 0.961904761904762
best_cv_scores: [1.         1.         0.95238095 0.85714286 1.        ]

对 KNN 模型的三个超参数 ------n_neighbors 、weights 、p 进行网络搜索（Grid Search） ，并用 5折交叉验证 评估每组参数的平均得分，找出性能最好的组合。

输出解析：

当 KNN 模型的参数设置为：

  • 邻居数（n_neighbors）= 9
  • 权重方式（weights）= 每个邻居权重相同（uniform）
  • 距离算法（p）= 2（欧式距离）

时，模型在 5 折交叉验证中的平均准确率是 96.2%。

模型误差

准确：

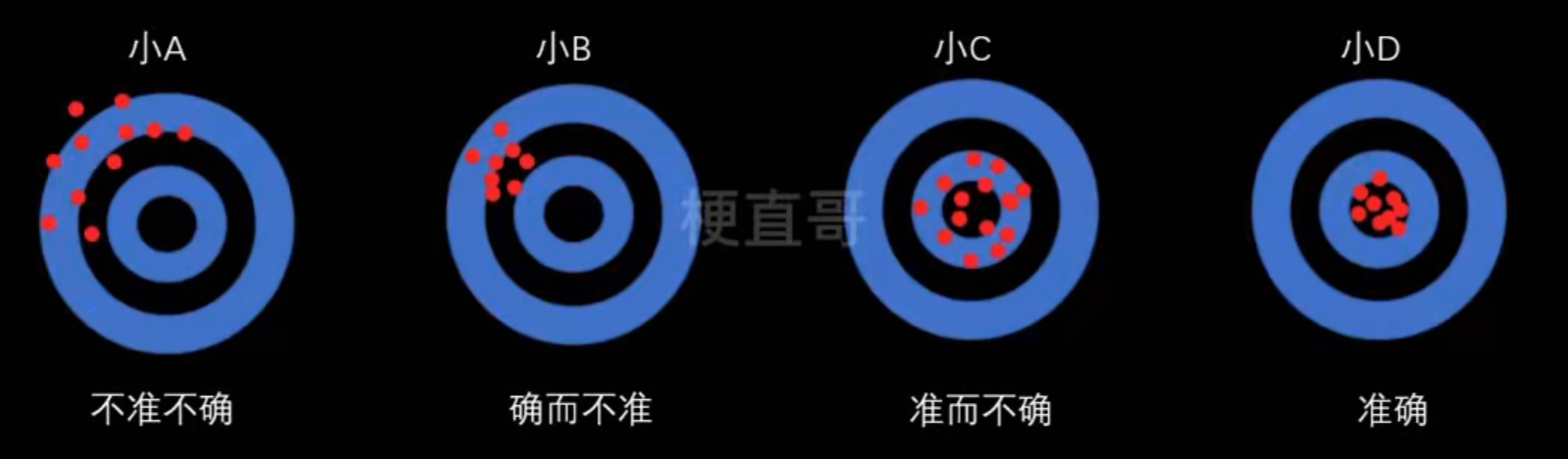
B的点比较集中，也就是比较确定

偏差、方差和噪声

模型误差的组成：

  • 高偏差的原因：模型本身不适合（线性模型拟合非线性数据）；欠拟合（模型未收敛）
  • 高方差的原因：模型过于复杂（特征太多）；过拟合（噪声数据影响）
  • 噪声难以避免的原因：观测误差，计算机精度误差，方法误差

偏差和方差的关系：

情况 偏差 方差 示意
高偏差、低方差 箭都集中在靶子一角（方向错，但很稳定）
低偏差、高方差 箭散落在靶心周围（平均准，但不稳定）
高偏差、高方差 箭乱飞，既不准又不稳
低偏差、低方差 箭都集中在靶心（理想模型）

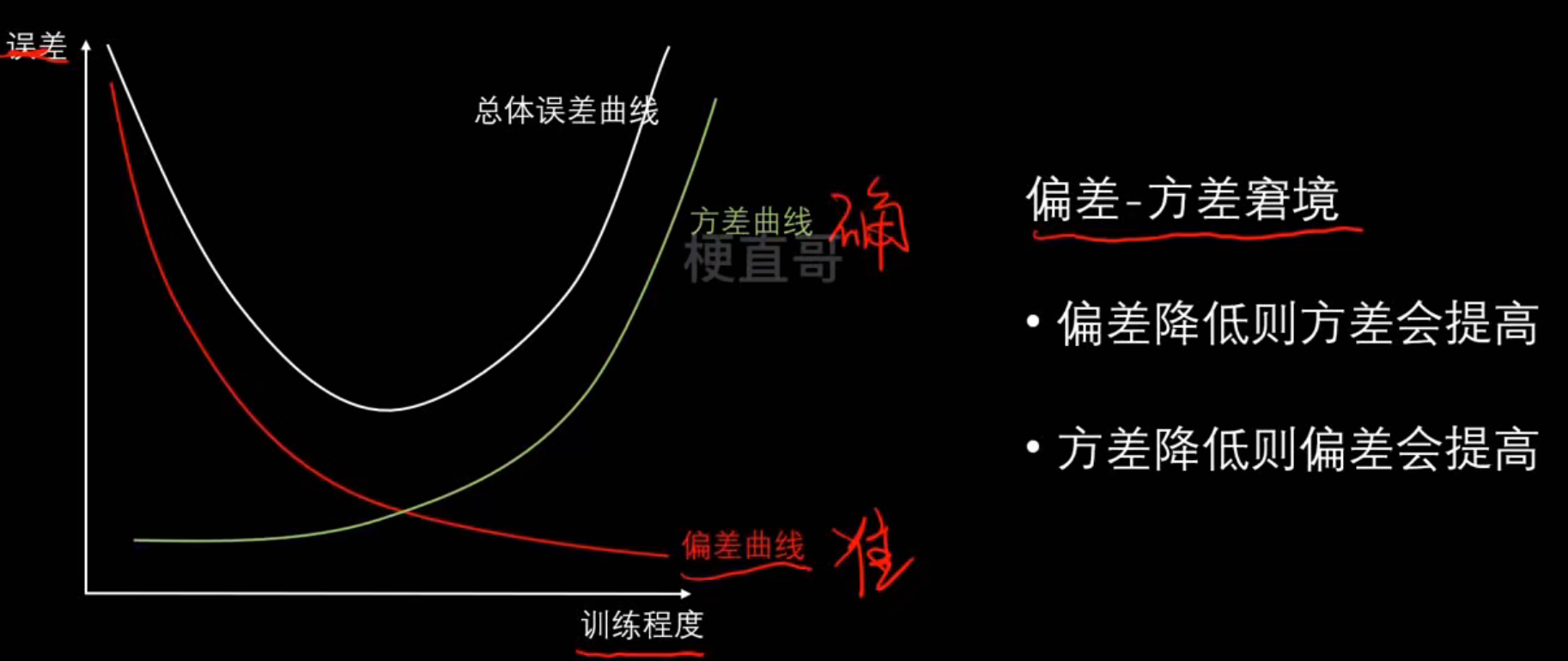
偏差、方差和模型复杂度的关系：

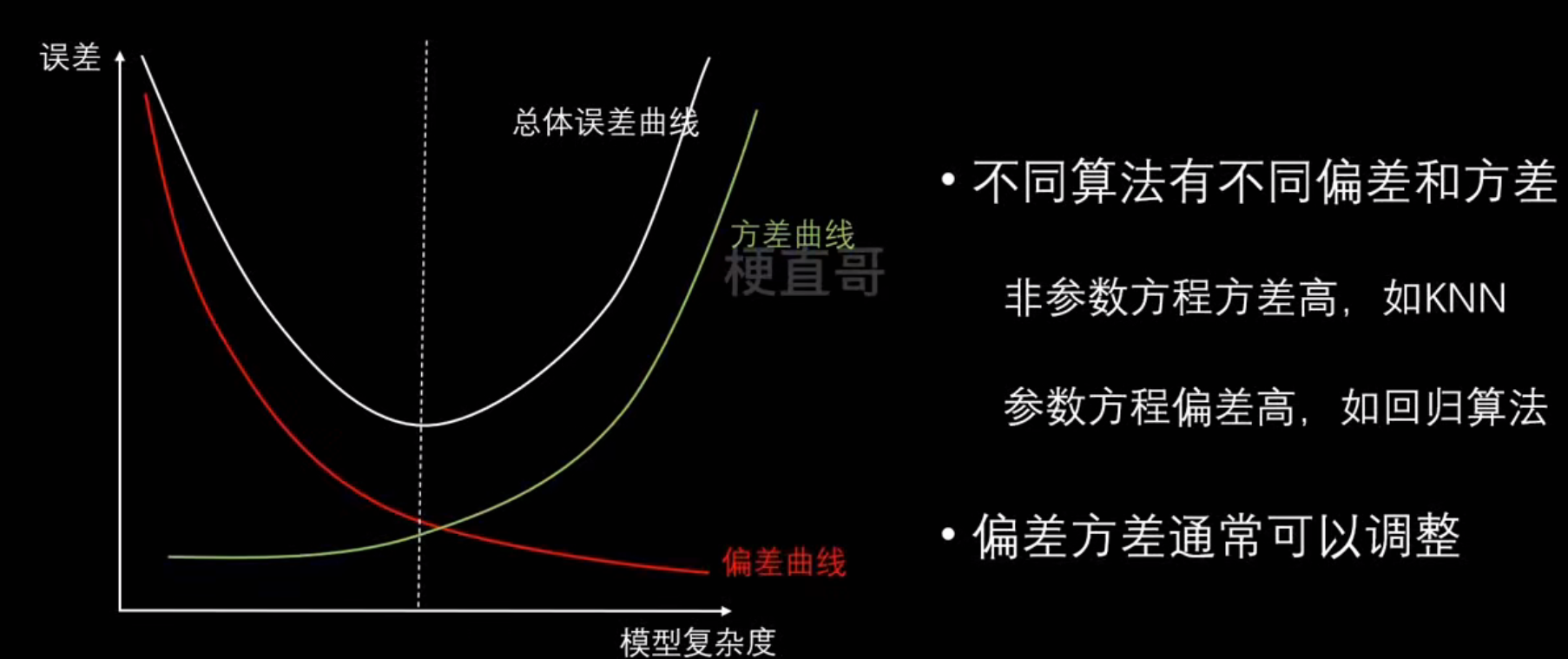
降低偏差：

  • 寻找更好的特征
  • 增加更多的特征
  • 提高模型复杂度

降低方差：

  • 尽量选低复杂度的模型
  • 尽可能增加样本数
  • 尽可能减少数据维度
  • 使用验证集
  • 使用正则化

正则化

本质上解决的是过拟合问题

在机器学习训练中，我们通常最小化一个**损失函数。**但是如果模型太复杂（比如参数太多、多层神经网络），它可能会"过度拟合训练集"，也就是把噪声也当成规律学了下来

为了防止这种情况，我们就给损失函数加一点"惩罚项" ，不让模型的参数随便乱跑、变得太大。这就是 正则化

  1. 多项式逼近思想：
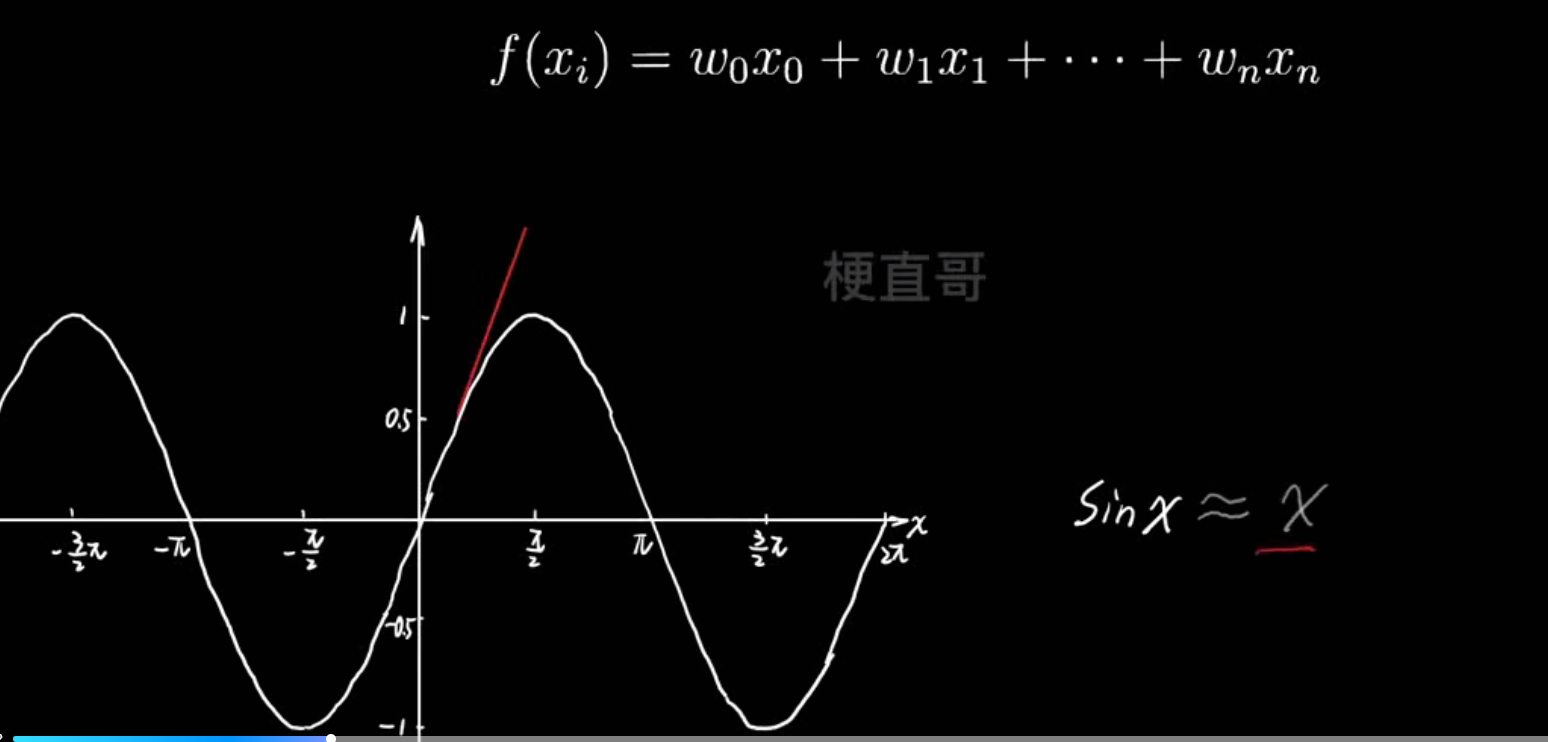
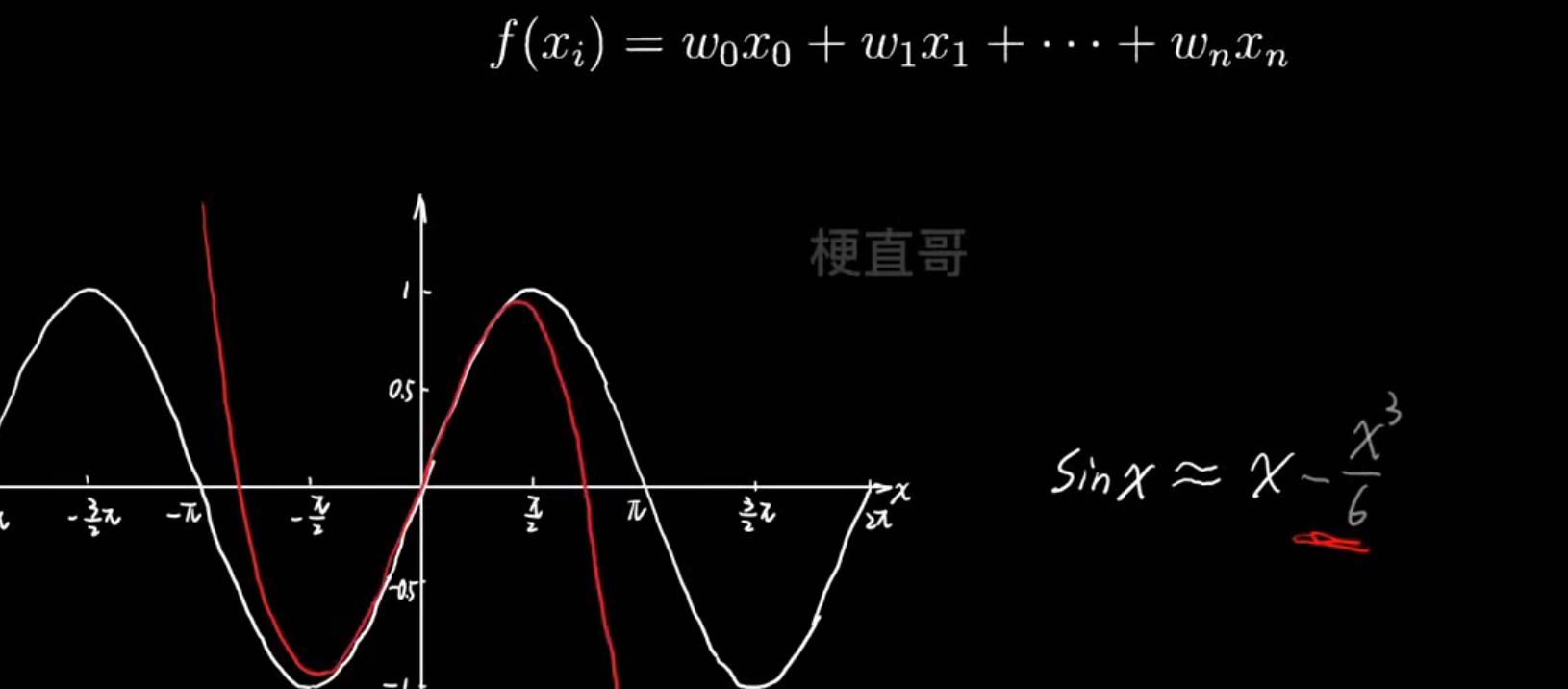
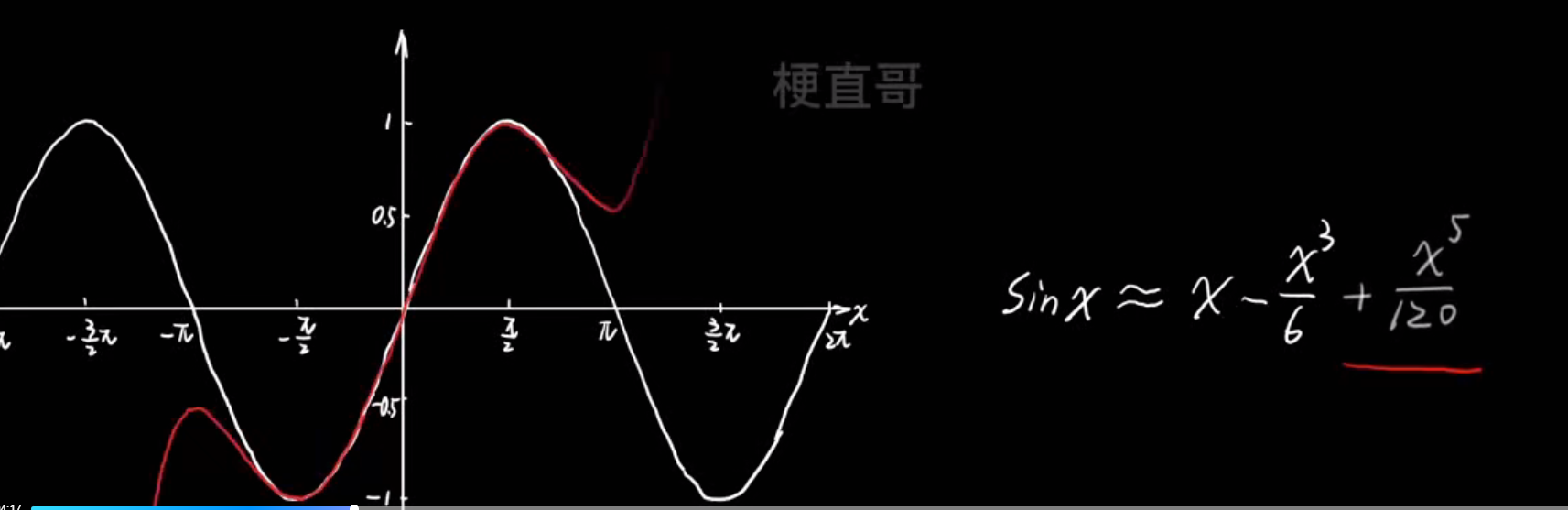
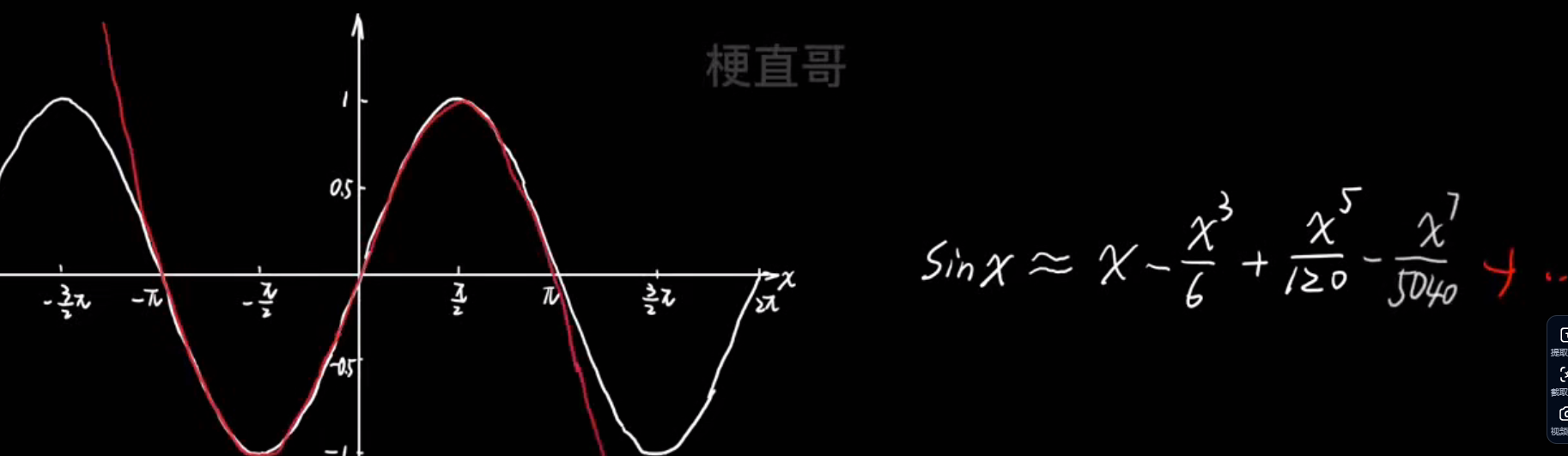
  1. 过拟合的真相：

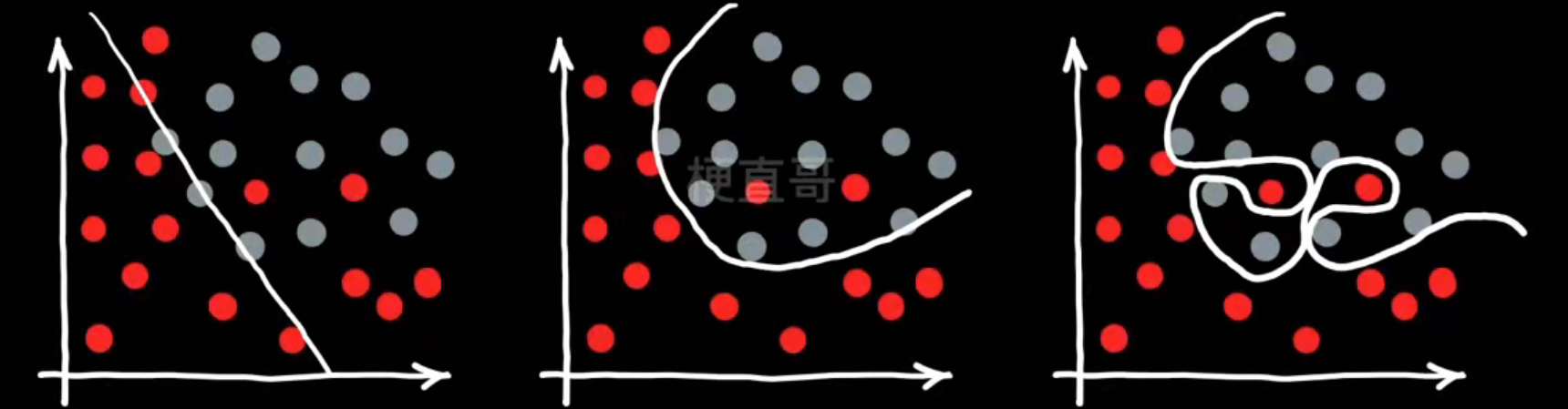
如何尽量避免第三种情况呢？

控制高次项的系数

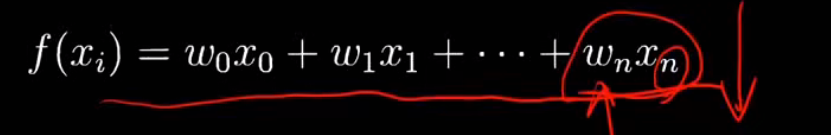
  1. 正则化

相似概念对比：

常见的两种正则化方法-----------LASSO回归和Ridge回归

模型泛化

泛化能力：

  • 机器学习算法对于新鲜样本的适应能力
  • 奥卡姆剃刀法则：能简单别复杂
  • 泛化理论：衡量模型复杂度

如何知道自己的模型是否理想？

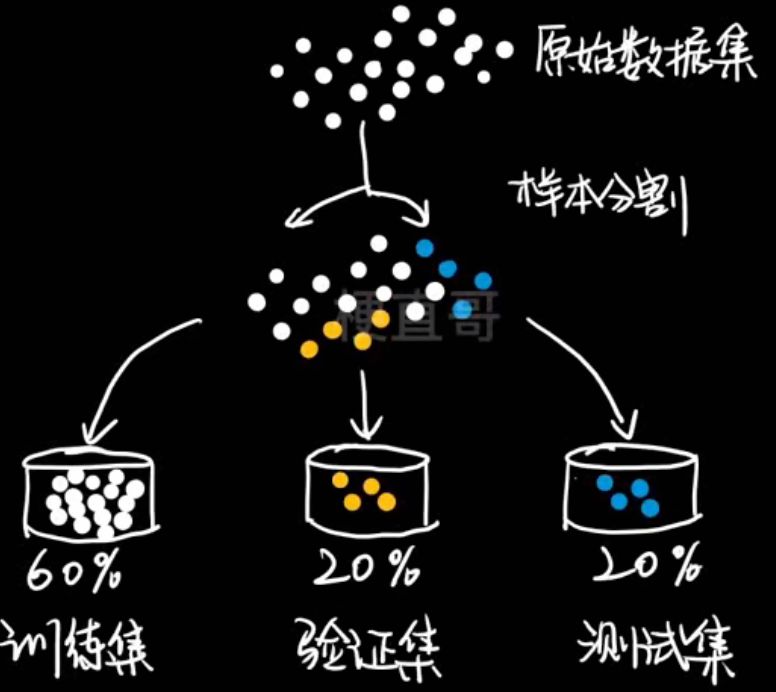
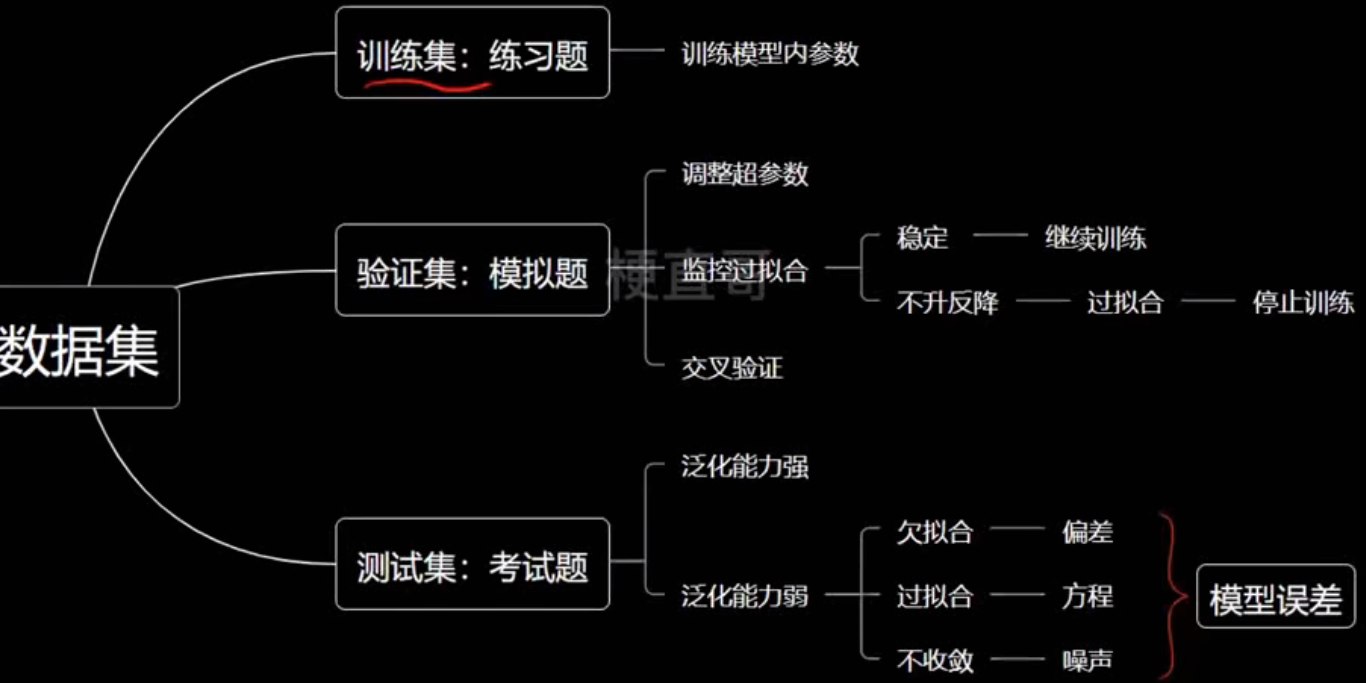
过拟合的应对策略：

  • 降低模型复杂度
  • 降低数据维度
  • 降噪
  • 增加样本数
  • 使用验证集
  • 正则化：
    • L1:LASSOR回归
    • L2：Ridge回归
    • L1+L2：弹性网络

评价标准：混淆矩阵、精确率和召回率

Precision，Recall,F1 Score

  1. 混淆矩阵Confusion Matrix
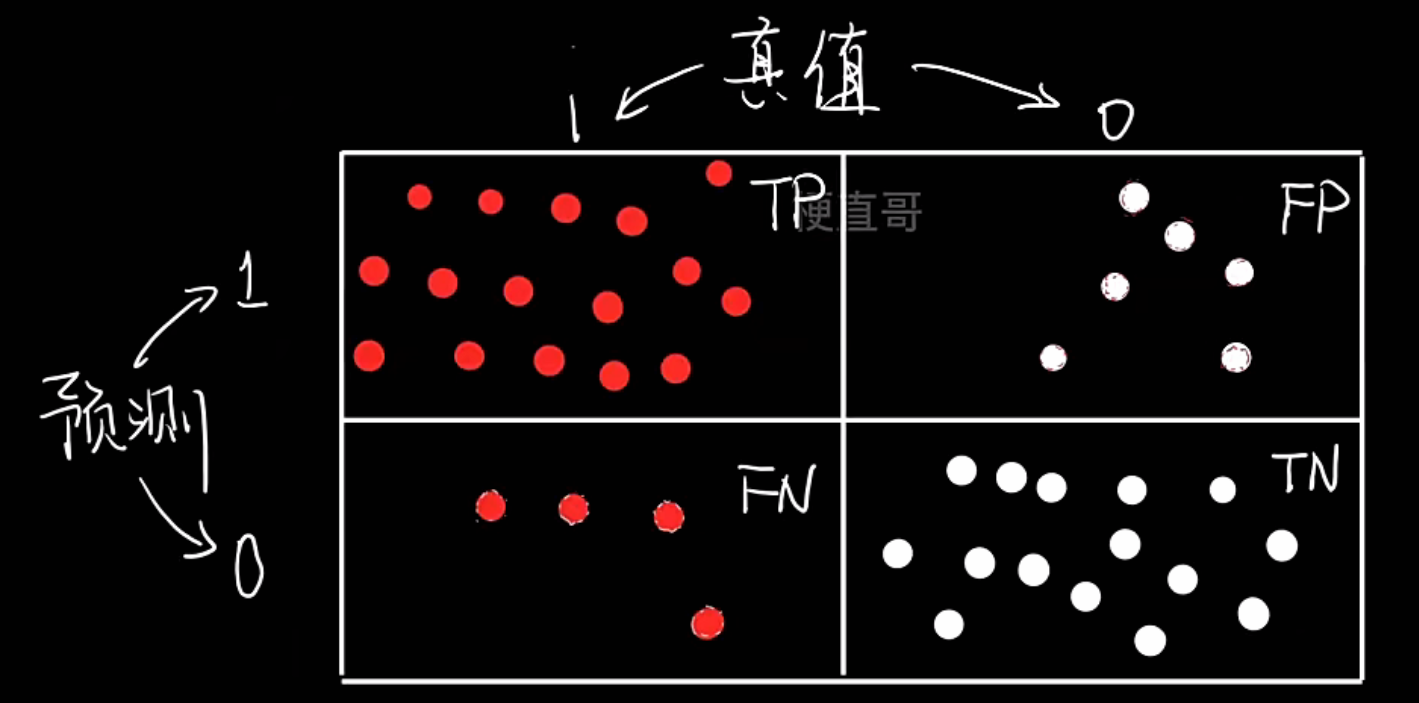
  1. 基于混淆矩阵的评价指标
指标 英文名 公式 含义
准确率 Accuracy (TP + TN) / (TP + FP + FN + TN) 预测正确的总体比例
精确率 Precision TP / (TP + FP) 预测为正的样本中，有多少是真的正
召回率 Recall TP / (TP + FN) 所有真实正样本中，被模型识别出来的比例
F1 值 F1-Score 2×(P×R)/(P+R) Precision 与 Recall 的综合平衡

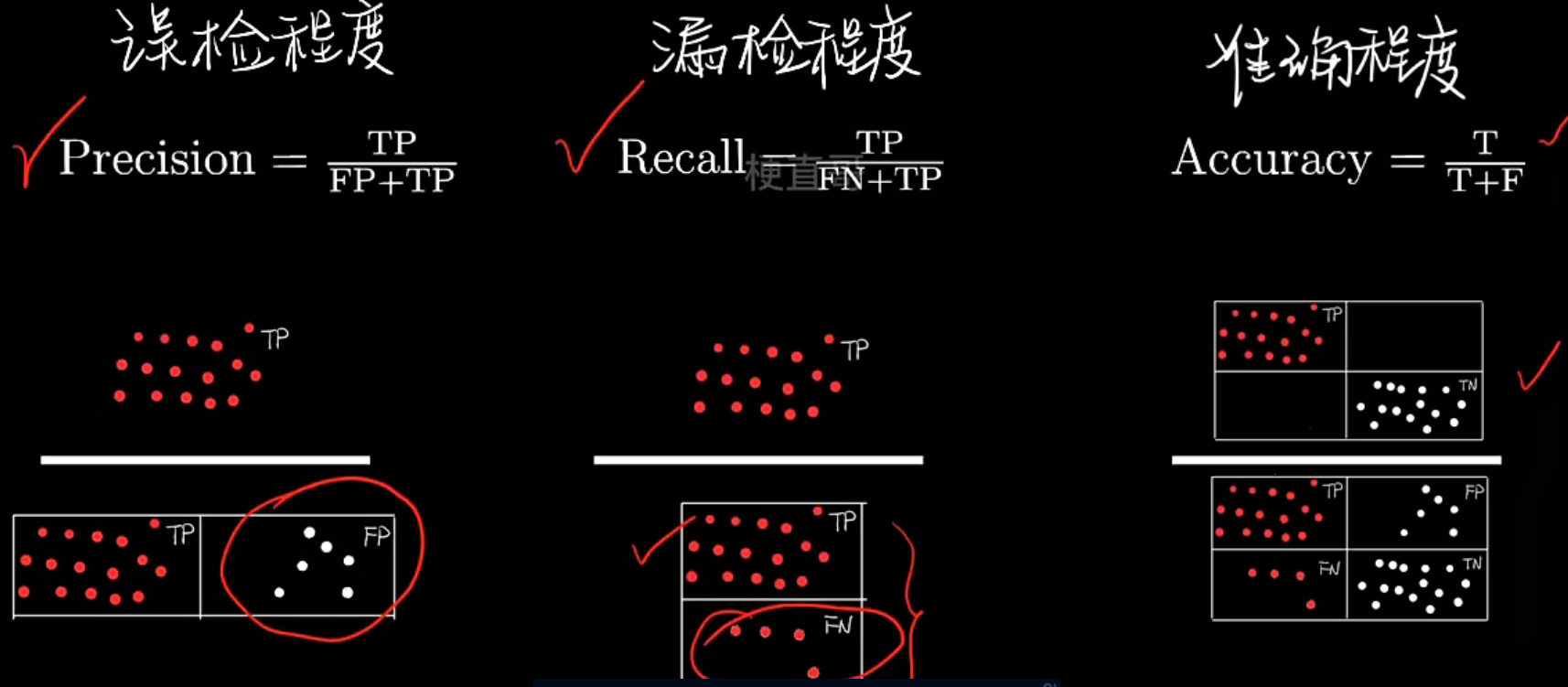
举个例子：

python 复制代码 
# 加载鸢尾花数据集
from sklearn import datasets
import numpy as np

iris=datasets.load_iris()
X=iris.data
y=iris.target.copy()
y

输出：
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
python 复制代码 
# 转化为二分类问题
y[y!=0]=1
y

输出：
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])
名称 英文全称 含义 模型预测结果 实际标签 是否预测正确
TP True Positive 真正例 正 正 ✅
FP False Positive 假正例 正 负 ❌
FN False Negative 假负例 负 正 ❌
TN True Negative 真负例 负 负 ✅
python 复制代码 
# 手动实现
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=666)

logistic_regression=LogisticRegression()
logistic_regression.fit(X_train,y_train)
y_predict=logistic_regression.predict(X_test)

TN=np.sum((y_predict==0)&(y_test==0))  #10
FP=np.sum((y_predict==1)&(y_test==0))  #0
FN=np.sum((y_predict==0)&(y_test==1))  #0
TP=np.sum((y_predict==1)&(y_test==1))  #28

confusion_matrix=np.array([
    [TN,FP],
    [FN,TP]
])
confusion_matrix

输出：
array([[10,  0],
       [ 0, 28]])

求精确率，召回率，F1

python 复制代码 
precision=TP/(TP+FP)  #1.0
recall=TP/(TP+FN)  #1.0
f1_score=2*precision*recall/(precision+recall) #1.0
python 复制代码 
# scikit-learn封装实现
from sklearn.metrics import confusion_matrix

confusion_matrix(y_test,y_predict)
输出：
array([[10,  0],
       [ 0, 28]])

from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import f1_score

precision_score(y_test,y_predict) #1.0
recall_score(y_test,y_predict)  #1.0
f1_score(y_test,y_predict)  #1.0

评价指标：ROC曲线

  1. ROC曲线

ROC 曲线（接收者操作特征曲线）是一个展示分类模型在不同阈值下性能表现的图，横轴是假阳性率（FPR），纵轴是真阳性率（TPR）

坐标 名称 公式 含义
X 轴 FPR（False Positive Rate） FP / (FP + TN) 实际为负却被误判为正的比例（误报率）
Y 轴 TPR（True Positive Rate）= Recall TP / (TP + FN) 实际为正被正确识别出来的比例（召回率）
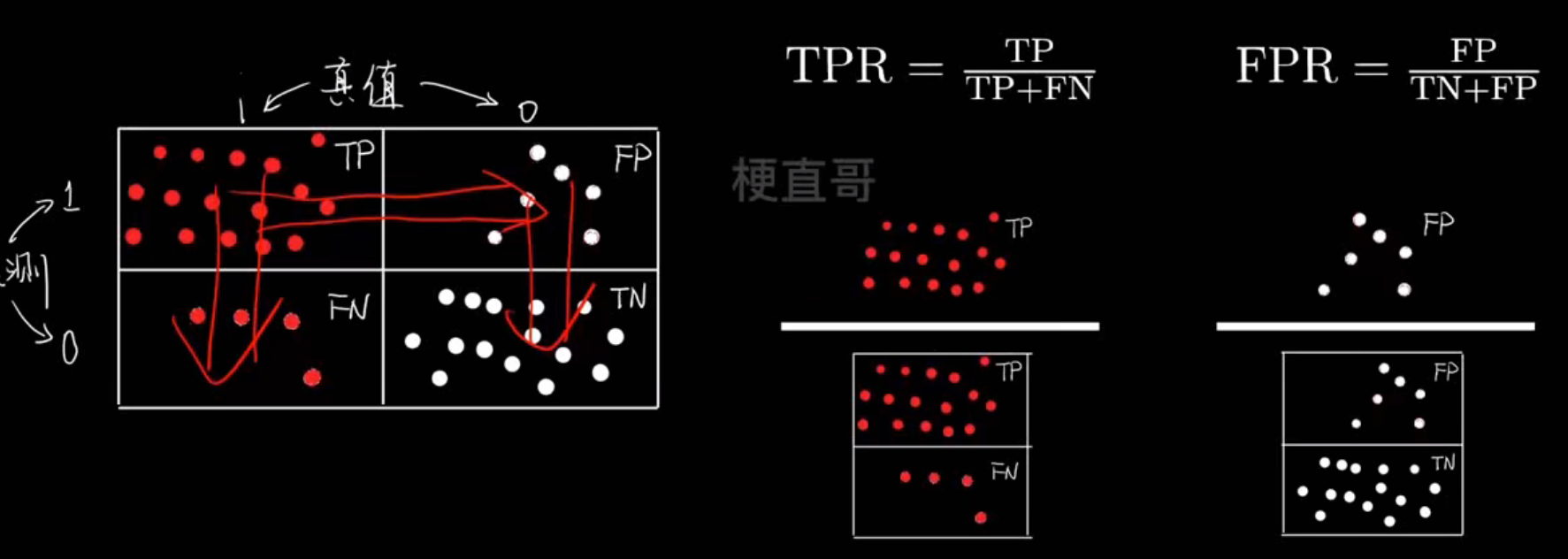
  1. PR曲线

**PR 曲线（Precision--Recall Curve）**是在二分类问题中，用来评估模型性能的一种重要可视化方法。它展示了模型在不同阈值（threshold）下，Precision（查准率） 和 Recall（查全率） 之间的关系

对比项 ROC 曲线 PR 曲线
横轴 FPR（假正率） Recall（召回率）
纵轴 TPR（真正率） Precision（精确率）
衡量内容 模型整体区分能力（看模型能不能区分正负） 模型在正类预测上的表现（看抓正类抓得多准、多全）
是否受类别比例影响 ❌ 不敏感 ✅ 非常敏感
适用场景 正负样本数量接近时 正样本稀少时（类别极不平衡）
典型任务 图像分类、性别识别 疾病检测、欺诈识别、垃圾邮件过滤
对应指标 AUC（ROC） AUC-PR
曲线表现 对角线表示随机分类 Precision 平均值接近正类比例表示随机分类
  1. AUC

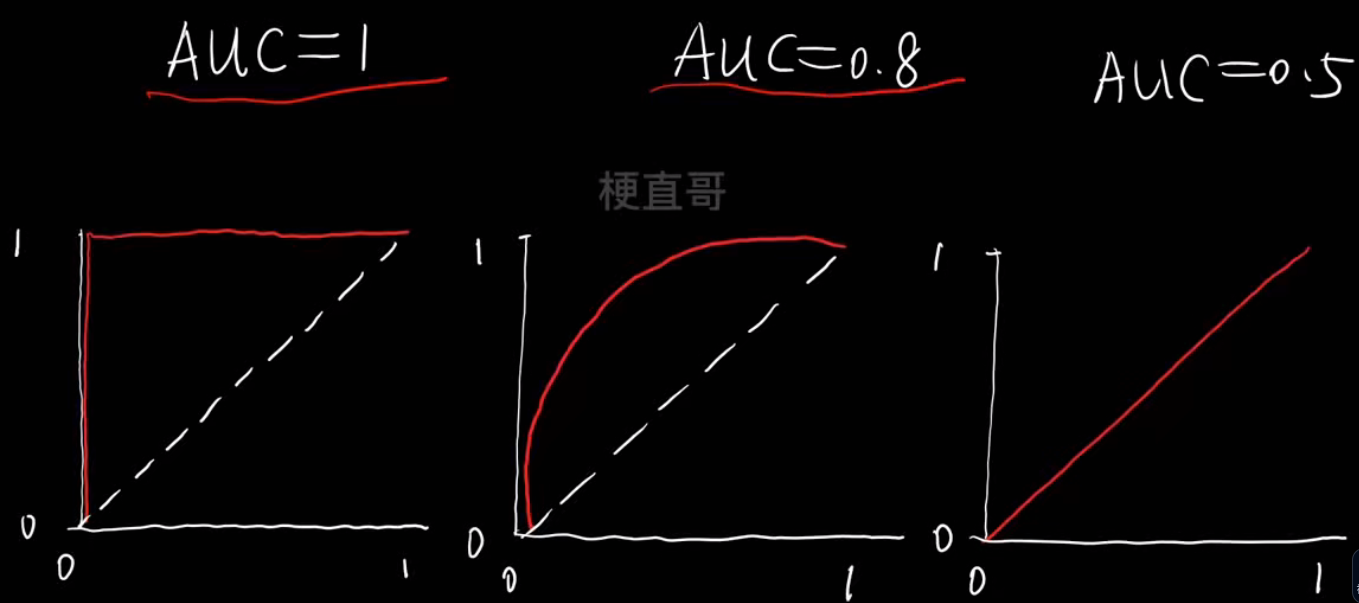
AUC (Area Under the Curve) 就是 ROC 曲线下的面积 ，

用一个数值（0～1之间）来衡量模型的整体分类能力。

它表示：

随机取一个正样本和一个负样本，

模型把正样本排在负样本前面的概率。

AUC的判断标准：

举个例子：

前置准备：

python 复制代码 
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

iris = datasets.load_iris()
X = iris.data
y = iris.target.copy()

# 转化为二分类问题
y[y!=0] = 1

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

logistic_regression = LogisticRegression()
logistic_regression.fit(X_train,y_train)
y_predict = logistic_regression.predict(X_test)
y_predict

输出：
array([1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0,
       1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1])

决策分数：

模型先给每个样本打一个分数，这个分数叫做"决策分数"（decision score）；然后根据这个分数再决定------到底判为正类还是负类

python 复制代码 
decision_scores = logistic_regression.decision_function(X_test)
decision_scores

输出：
array([ 4.52818505,  6.87901472,  1.76728414,  6.52488998, -3.69893489,
        3.62555304,  4.5641345 ,  6.91106486,  5.03499692,  4.3292245 ,
        4.65382011, -3.43985382, -3.38750347, -3.39712028,  9.14590416,
        3.55830077, -5.19913952,  8.64478135,  7.05911342,  7.24100241,
        5.13254176, -3.758013  , 11.76868021, -3.89433573,  4.27903572,
        4.01351394, -4.2488403 ,  3.78927124,  8.75367646,  9.69578918,
       -4.01142913, -3.69538324,  3.69140718,  7.14170805,  1.08284202,
        5.36638089,  7.40154878, 10.56568001])
python 复制代码 
# 手写绘制 Precision--Recall vs Threshold 曲线
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score

precision_scores = []
recall_scores = []
thresholds = np.sort(decision_scores)
for threshold in thresholds:
    # 大于阈值分为1，小于阈值分为0
    y_predict = np.array(decision_scores>=threshold,dtype='int')
    precision = precision_score(y_test,y_predict)
    recall = recall_score(y_test,y_predict)
    precision_scores.append(precision)
    recall_scores.append(recall)  

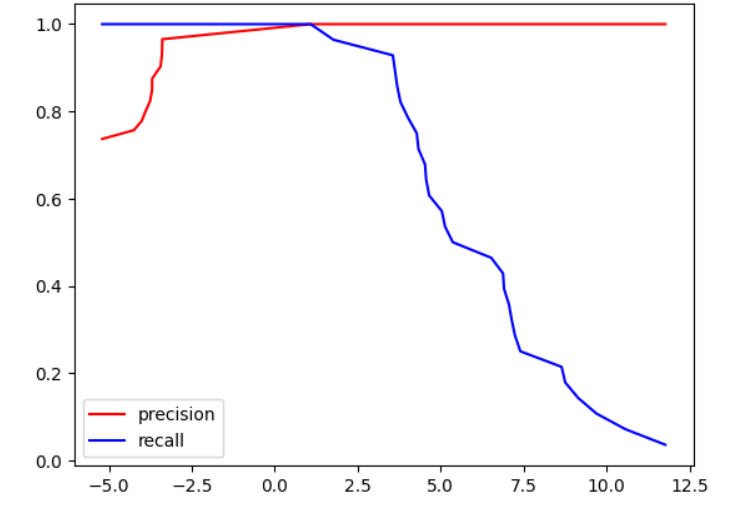
plt.plot(thresholds, precision_scores, color='r',label="precision")
plt.plot(thresholds, recall_scores, color='b',label="recall")
plt.legend()
plt.show()
元素 含义
横轴（x-axis） 决策阈值（threshold） = decision_function 的分界线
纵轴（y-axis） Precision 或 Recall（介于 0 和 1 之间）
红线（precision） 查准率------预测为正的样本中有多少是真的正样本
蓝线（recall） 查全率------所有真实正样本中被预测为正的比例

图形规律：

阈值变化方向 Precision（红线） Recall（蓝线） 模型行为
阈值 ↓ ↓ 降 ↑ 升 "激进"型：多报，查得全但误报多
阈值 ↑ ↑ 升 ↓ 降 "保守"型：少报，查得准但漏报多
python 复制代码 
# Precision-Recall 曲线，简称PR曲线
plt.plot(recall_scores,precision_scores)
plt.xlabel("Recall")
plt.ylabel("Precision")
plt.show()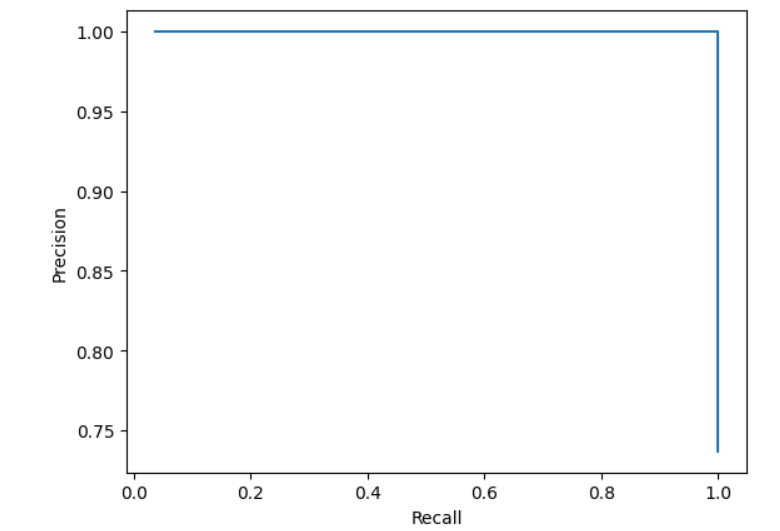
python 复制代码 
# scikit-learn中的PR曲线
from sklearn.metrics import precision_recall_curve

precision_scores, recall_scores,thresholds =  precision_recall_curve(y_test,decision_scores)

plt.plot(thresholds, precision_scores[:-1], color='r',label="precision")
plt.plot(thresholds, recall_scores[:-1], color='b',label="recall")
plt.legend()
plt.show()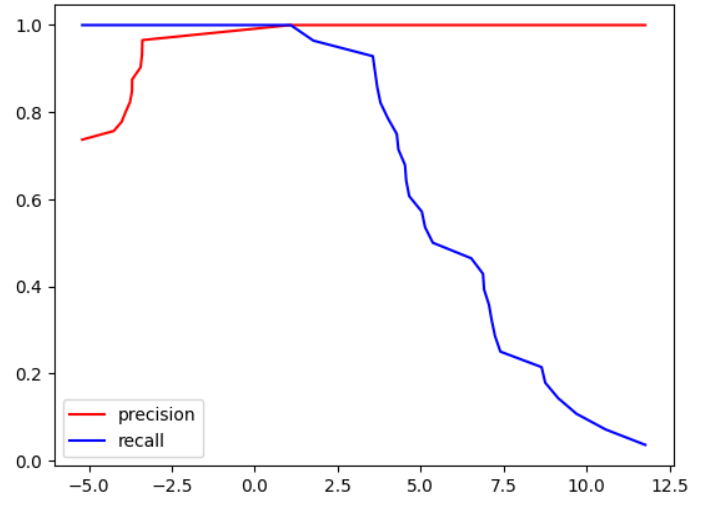
python 复制代码 
plt.plot(recall_scores,precision_scores)
plt.xlabel("Recall")
plt.ylabel("Precision")
plt.show()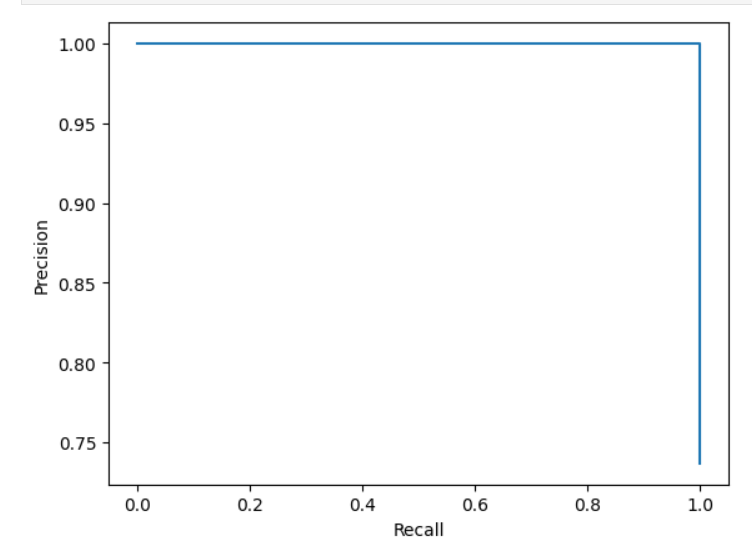
python 复制代码 
# scikit-learn中的ROC曲线
from sklearn.metrics import roc_curve

fpr, tpr, thresholds = roc_curve(y_test,decision_scores)
plt.plot(fpr,tpr)
plt.xlabel("FPR")
plt.ylabel("TPR")
plt.show()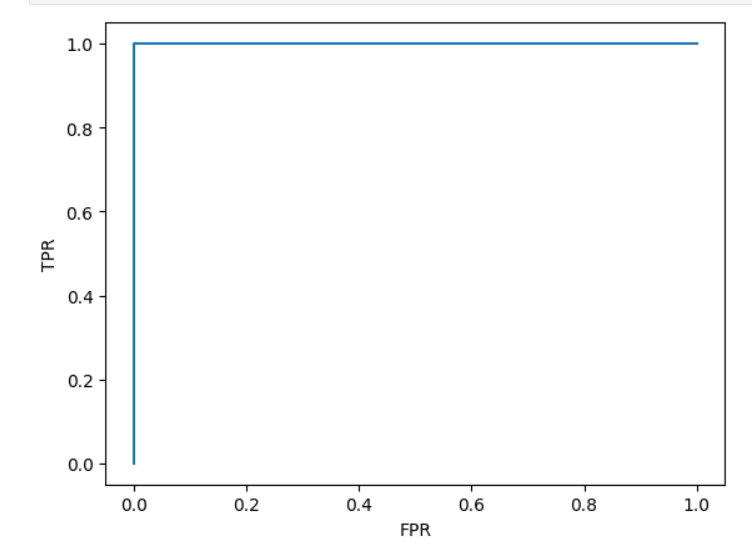
python 复制代码 
from sklearn.metrics import roc_auc_score

auc = roc_auc_score(y_test,decision_scores)
auc

输出：
np.float64(1.0)

4、决策树

树状决策：

  • 假设数据中隐含树状特征结构
  • 构建规则模型实现逼近
  • 数据自上而下实现分类

决策树核心思想和原理

决策树的样子：

决策树的生成：

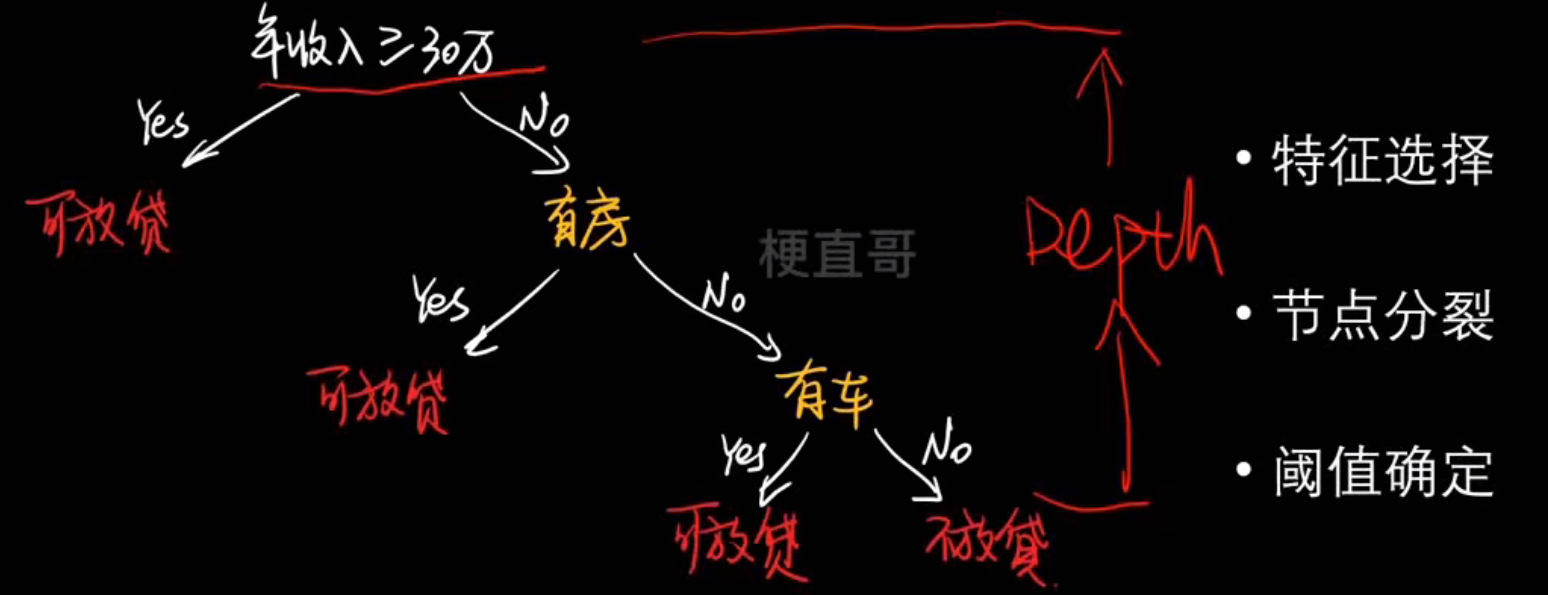
信息熵

  1. 信息熵
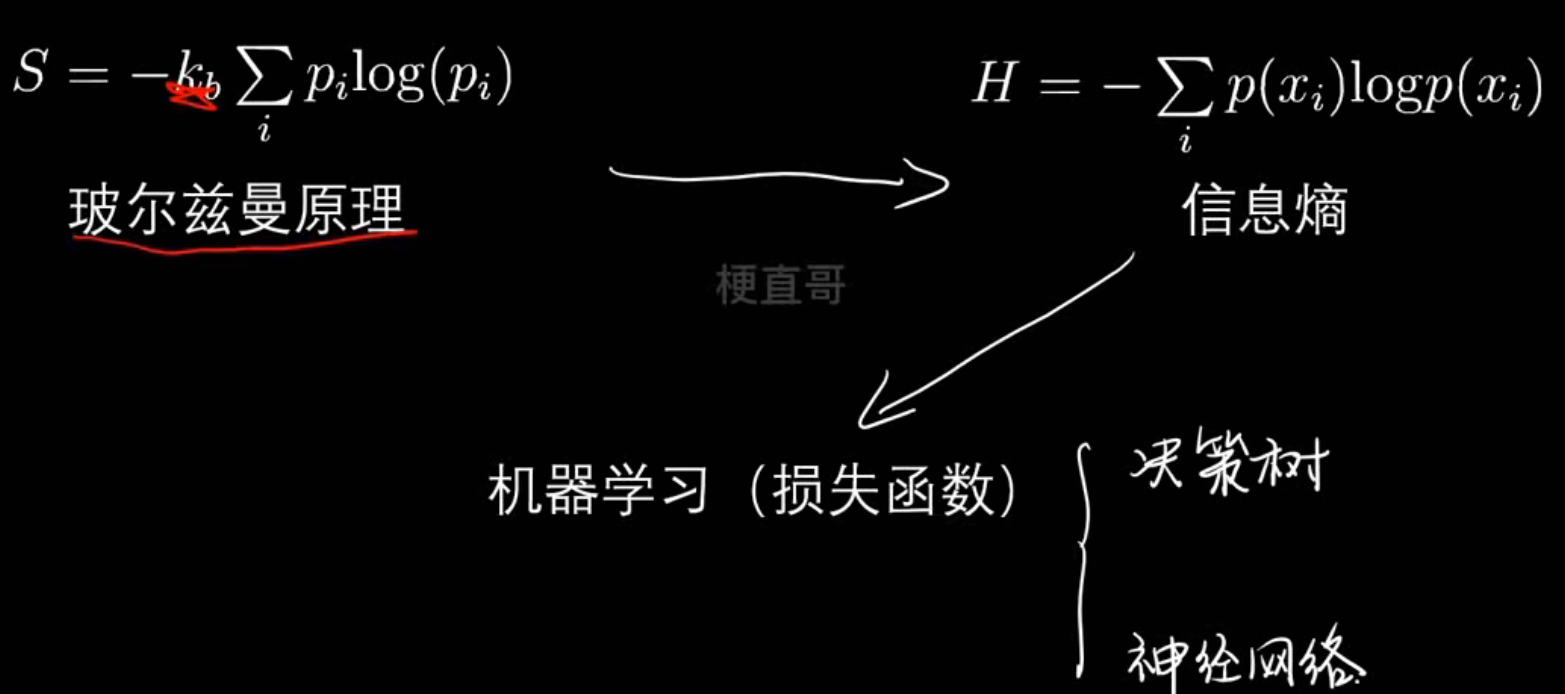
名称 含义 公式 应用场景
信息熵 (H§) 度量系统自身的不确定性 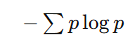决策树分类（选择划分）
交叉熵 (H(p,q)) 度量两个分布差异 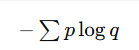分类模型的损失函数
MSE 预测值与真实值的距离平方 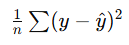回归任务损失函数
  1. 各种熵
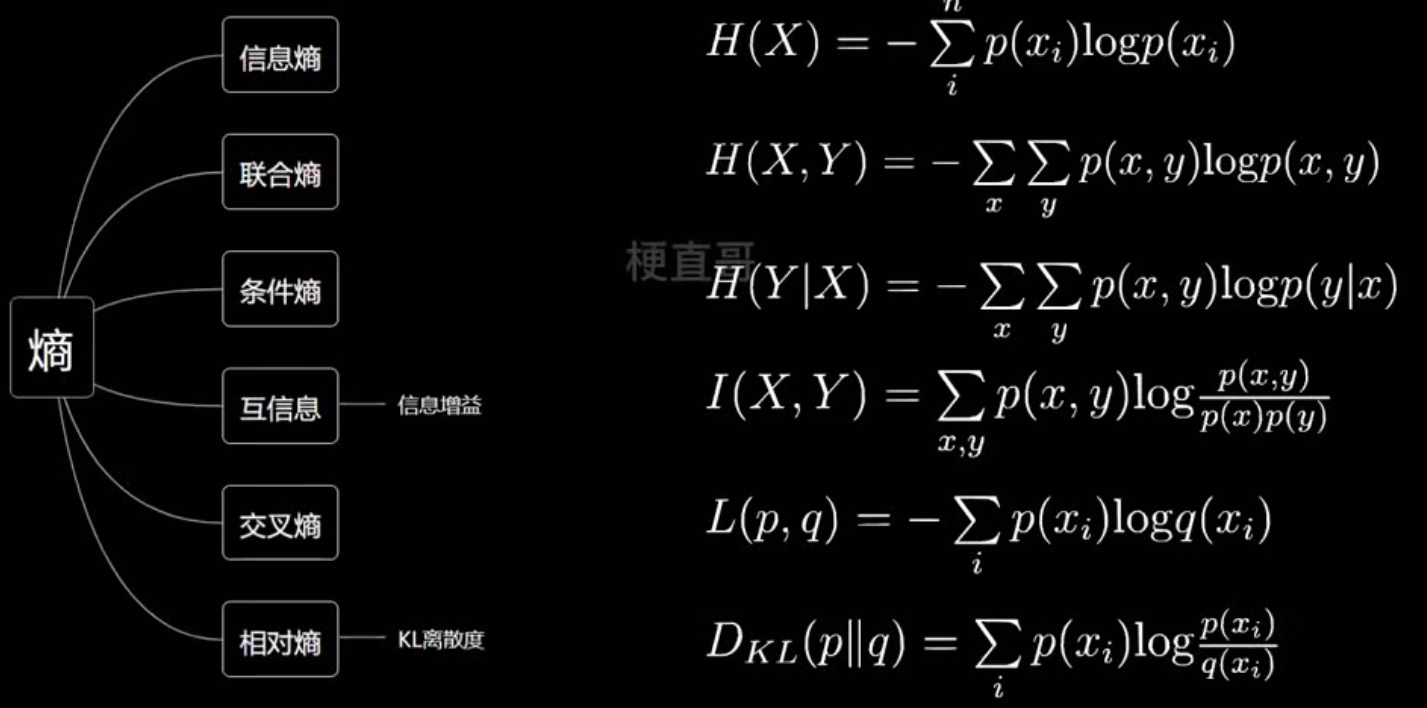
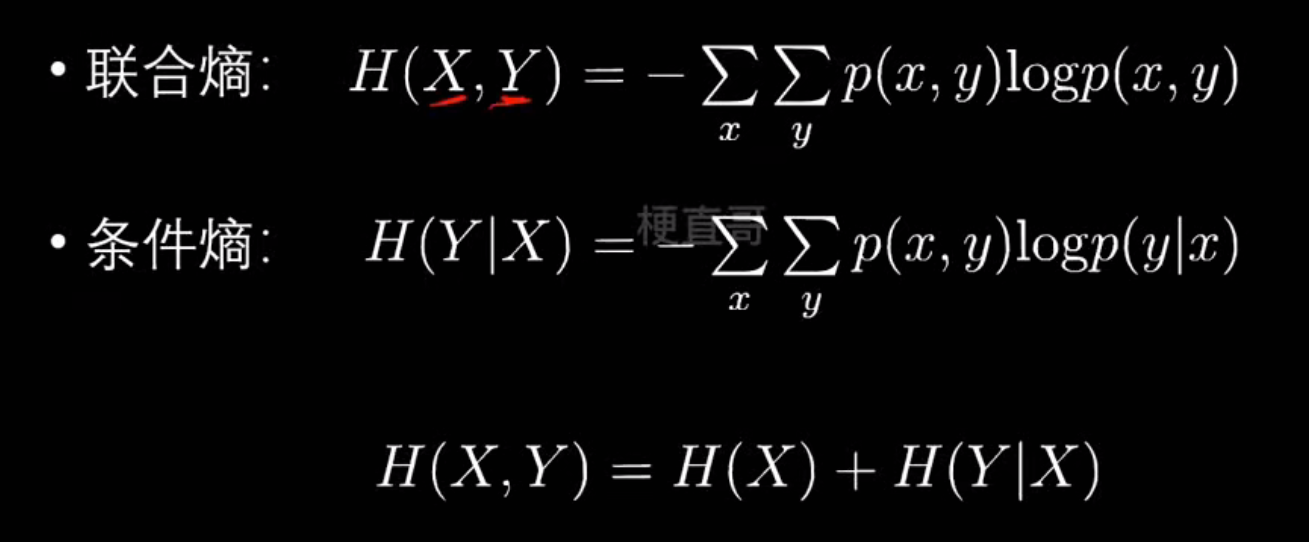
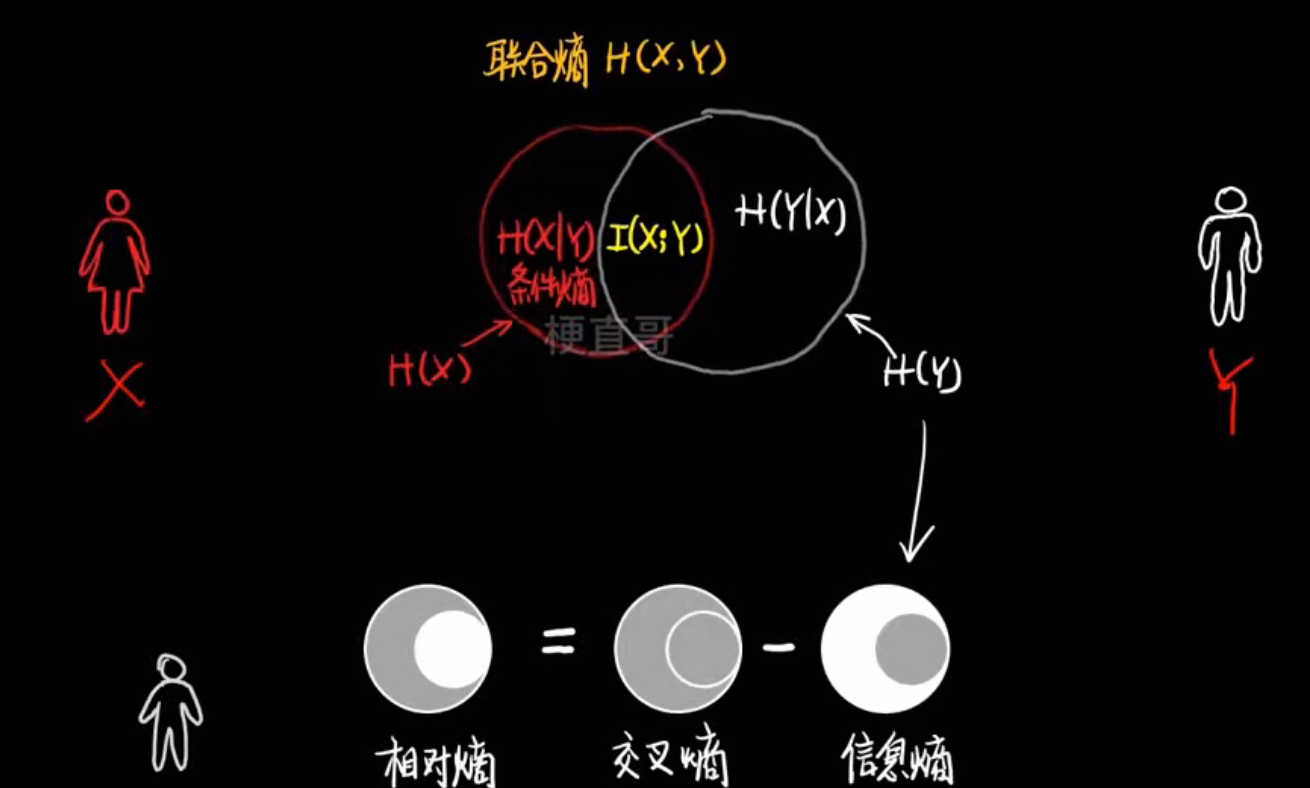
  1. 信息增益

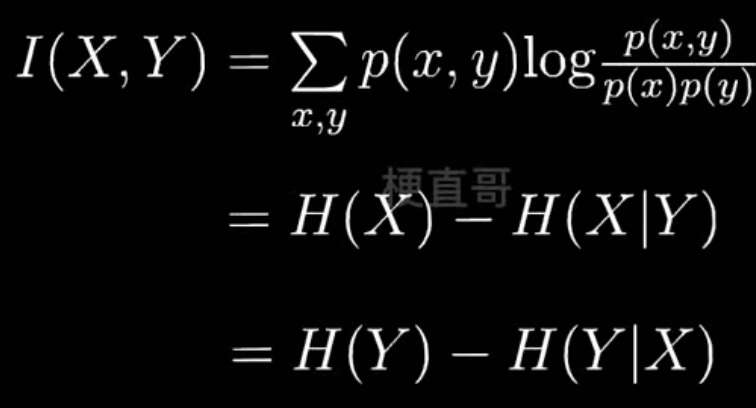
决策树分类任务和代码实现

python 复制代码 
# 二分类信息熵
import numpy as np
import matplotlib.pyplot as plt

def entropy(p):
    return -(p * np.log2(p) + (1 - p) * np.log2(1 - p))
plot_x = np.linspace(0.001, 0.999, 100)
plt.plot(plot_x, entropy(plot_x))
plt.show()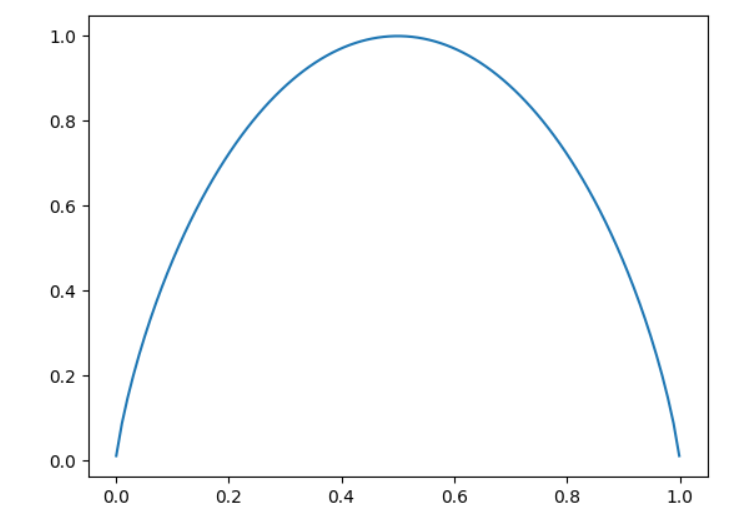
python 复制代码 
# 数据集
from sklearn.datasets import load_iris

iris = load_iris()
x = iris.data[:, 1:3]
y = iris.target
plt.scatter(x[:,0], x[:,1], c = y)
plt.show()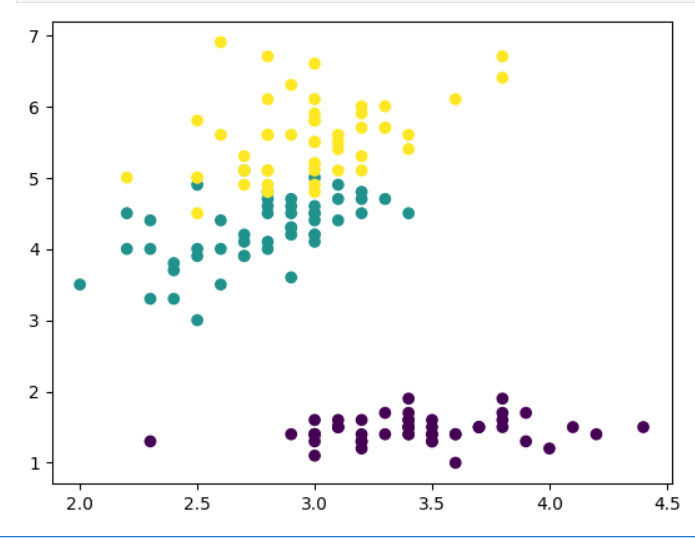
python 复制代码 
# 查看刚刚分类的效果
from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier(max_depth=2, criterion='entropy')
clf.fit(x, y)
def decision_boundary_plot(X, y, clf):
    axis_x1_min, axis_x1_max = X[:,0].min() - 1, X[:,0].max() + 1
    axis_x2_min, axis_x2_max = X[:,1].min() - 1, X[:,1].max() + 1
    
    x1, x2 = np.meshgrid( np.arange(axis_x1_min,axis_x1_max, 0.01) , np.arange(axis_x2_min,axis_x2_max, 0.01))
    z = clf.predict(np.c_[x1.ravel(),x2.ravel()])
    z = z.reshape(x1.shape)
    
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#F5B9EF','#BBFFBB','#F9F9CB'])

    plt.contourf(x1, x2, z, cmap=custom_cmap)
    plt.scatter(X[:,0], X[:,1], c=y)
    plt.show()

decision_boundary_plot(x, y, clf)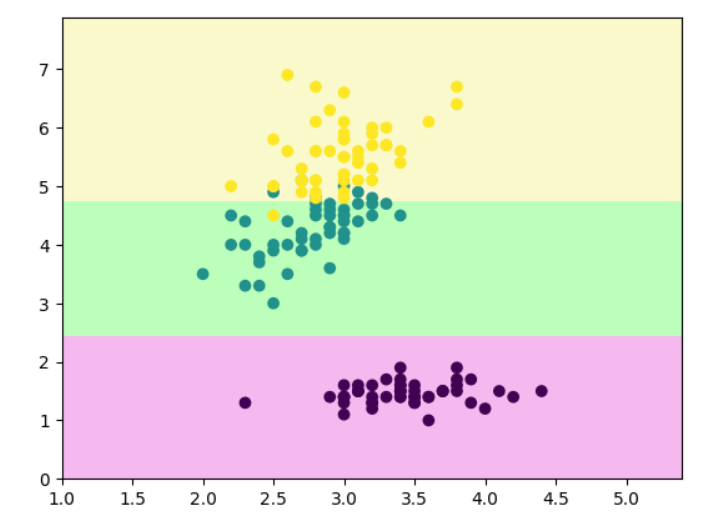
python 复制代码 
# sklearn中的决策树
from sklearn.tree import plot_tree
plot_tree(clf)

决策树的"最优划分条件"就是在每一步划分时，选择能让数据"最纯净"的特征和分割点

python 复制代码 
for 每个特征:
    for 每个候选划分点:
        → 按阈值划分样本
        → 计算左右熵
        → 计算加权平均熵
        → 若小于当前最小熵 → 更新最优划分
python 复制代码 
# 最优划分条件
# 用 Python 的计数器统计每个类别在样本中出现的次数，得到每类样本数。
from collections import Counter
Counter(y)  #Counter({np.int64(0): 50, np.int64(1): 50, np.int64(2): 50})
#  手写实现计算数据集的熵
def calc_entropy(y):
    counter = Counter(y)
    sum_ent = 0
    for i in counter:
        p = counter[i] / len(y)
        sum_ent += (-p * np.log2(p))
    return sum_ent
calc_entropy(y)  #np.float64(1.584962500721156)

def split_dataset(x, y, dim, value):
    index_left = (x[:, dim] <= value)
    index_right = (x[:, dim] > value)
    return x[index_left], y[index_left], x[index_right], y[index_right]
def find_best_split(x, y):
    best_dim = -1
    best_value = -1
    best_entropy = np.inf
    best_entropy_left, best_entropy_right = -1, -1
    for dim in range(x.shape[1]):
        sorted_index = np.argsort(x[:, dim])
        for i in range(x.shape[0] - 1):
            value_left, value_right = x[sorted_index[i], dim], x[sorted_index[i + 1], dim]
            if value_left != value_right:
                value = (value_left + value_right) / 2
                x_left, y_left, x_right, y_right = split_dataset(x, y, dim, value)
                entropy_left, entropy_right = calc_entropy(y_left), calc_entropy(y_right)
                entropy = (len(x_left) * entropy_left + len(x_right) * entropy_right) / x.shape[0]
                if entropy < best_entropy:
                    best_dim = dim
                    best_value = value
                    best_entropy = entropy
                    best_entropy_left, best_entropy_right = entropy_left, entropy_right
    return best_dim, best_value, best_entropy, best_entropy_left, best_entropy_right
find_best_split(x, y)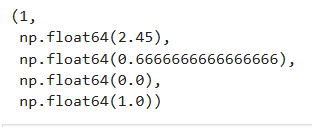
python 复制代码 
x_left, y_left, x_right, y_right = split_dataset(x, y, 1, 2.45)
find_best_split(x_right, y_right)

基尼系数

在分类问题中，我们希望每个节点（或样本集合）尽可能"纯"（pure），也就是样本尽量属于同一个类别。

基尼系数（Gini Impurity）就是用来衡量一个节点的不纯度的指标。

  • 纯度高：节点中样本几乎都属于同一类 → 基尼系数小；
  • 纯度低：节点中样本类别分布混乱 → 基尼系数大。
情形 类别分布 计算 Gini值 解释
完全纯 A类=100% (1 - 1^2 = 0) 0 最纯，节点完美
二分类均匀 A=50%，B=50% 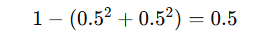0.5 最不纯
A=70%，B=30% 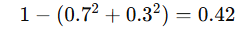0.42 有一定纯度

应用----决策树在划分节点时，会遍历所有特征和可能的划分点，计算：

  1. 划分后的左右子节点的基尼系数；
  2. 计算加权平均基尼系数（即划分后的整体纯度）；
  3. 选取加权基尼最小的划分作为最优划分

代码实现：

python 复制代码 
import numpy as np
import matplotlib.pyplot as plt

def entropy(p):
    return -(p * np.log2(p) + (1 - p) * np.log2(1 - p))
def gini(p):
    return 1 - p ** 2 - (1 - p) ** 2
plot_x = np.linspace(0.001, 0.999, 100)
plt.plot(plot_x, entropy(plot_x), color = 'blue')
plt.plot(plot_x, gini(plot_x), color = 'red')
plt.show()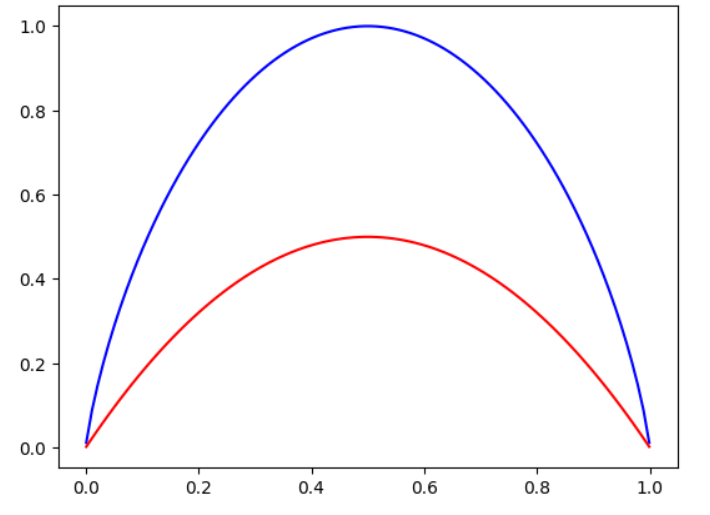

基尼系数和信息熵

  • 基尼系数运算稍快
  • 物理意义略有不同
  • 模型效果上差异不大
python 复制代码 
clf = DecisionTreeClassifier(max_depth=2, criterion='gini')
clf.fit(x, y)

注意！如果不指定，默认就是用基尼系数划分

决策树剪枝

为什么要剪枝？

  • 目标：
    • 降低复杂度，提高模型泛化能力
    • 解决过拟合
  • 手段：
    • 限制深度（结点层数）
    • 限制广度（叶子结点个数）

举个例子对比一下剪枝和不剪枝的区别：

不剪枝：

python 复制代码 
# 准备数据集
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris

iris=load_iris()
x=iris.data[:,0:2]
y=iris.target

plt.scatter(x[:,0],x[:,1],c=y)
plt.show()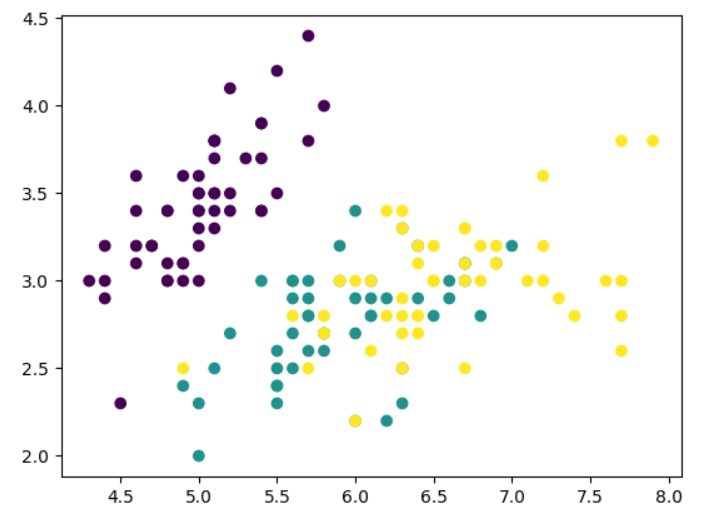
python 复制代码 
# 使用决策树算法拟合样本数据
from sklearn.tree import DecisionTreeClassifier

clf=DecisionTreeClassifier()
clf.fit(x,y)

def decision_boundary_plot(X, y, clf):
    axis_x1_min, axis_x1_max = X[:,0].min() - 1, X[:,0].max() + 1
    axis_x2_min, axis_x2_max = X[:,1].min() - 1, X[:,1].max() + 1
    
    x1, x2 = np.meshgrid( np.arange(axis_x1_min,axis_x1_max, 0.01) , np.arange(axis_x2_min,axis_x2_max, 0.01))
    z = clf.predict(np.c_[x1.ravel(),x2.ravel()])
    z = z.reshape(x1.shape)
    
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#F5B9EF','#BBFFBB','#F9F9CB'])

    plt.contourf(x1, x2, z, cmap=custom_cmap)
    plt.scatter(X[:,0], X[:,1], c=y)
    plt.show()
# 绘制决策边界来查看绘制效果
decision_boundary_plot(x,y,clf)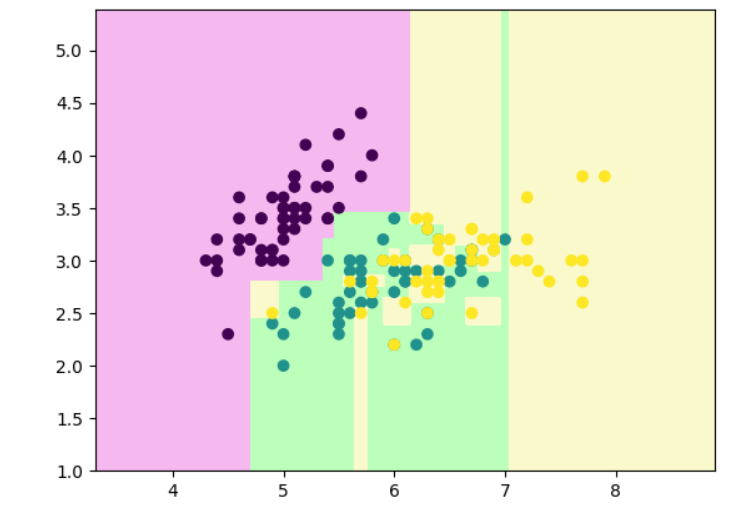
python 复制代码 
# 绘制决策树样子
from sklearn.tree import plot_tree
plot_tree(clf)

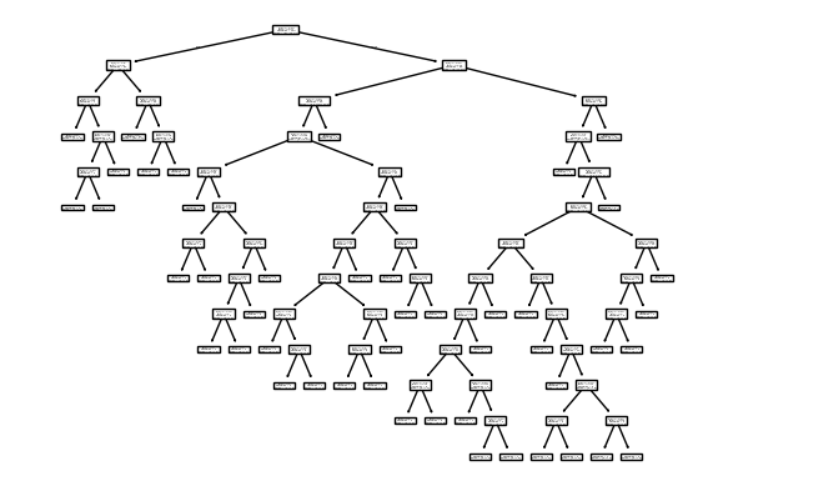
剪枝后：

python 复制代码 
# 决策树剪枝
clf=DecisionTreeClassifier(max_depth=4)  #深度
clf.fit(x,y)
decision_boundary_plot(x,y,clf)
plot_tree(clf)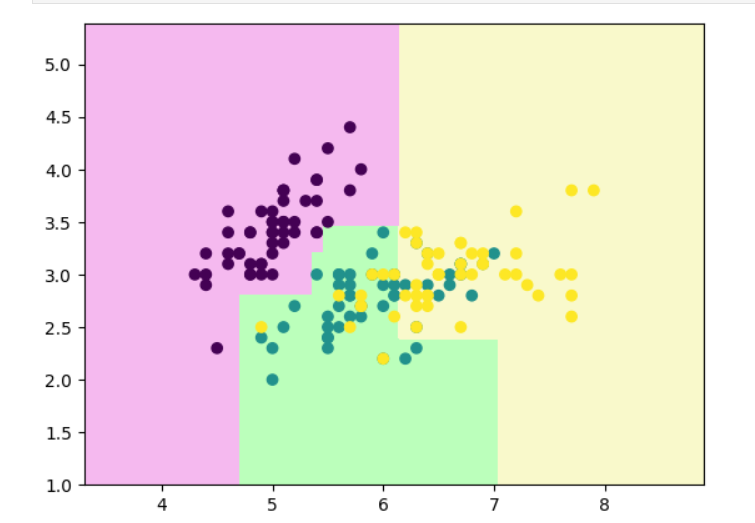
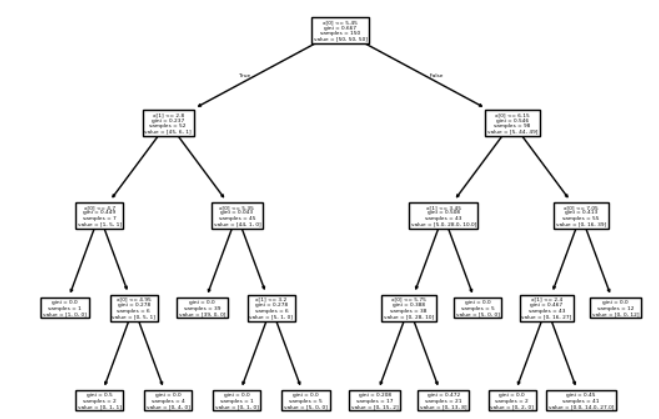
python 复制代码 
# 最小样本划分
clf=DecisionTreeClassifier(min_samples_split=20)  
clf.fit(x,y)
decision_boundary_plot(x,y,clf)
plot_tree(clf)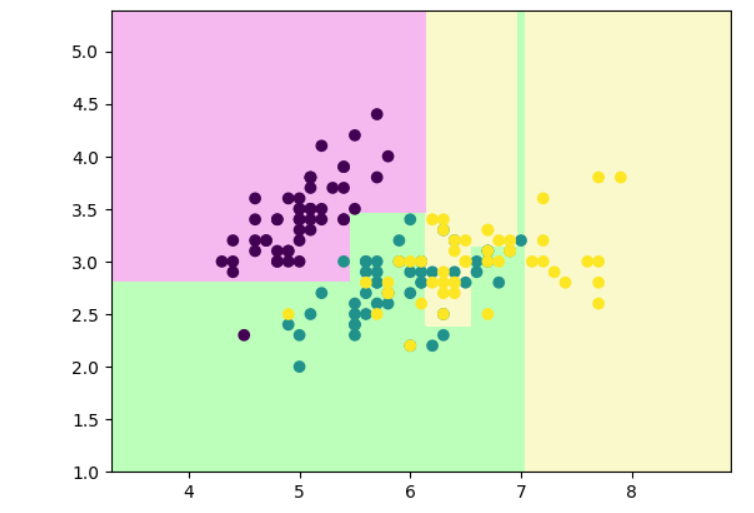
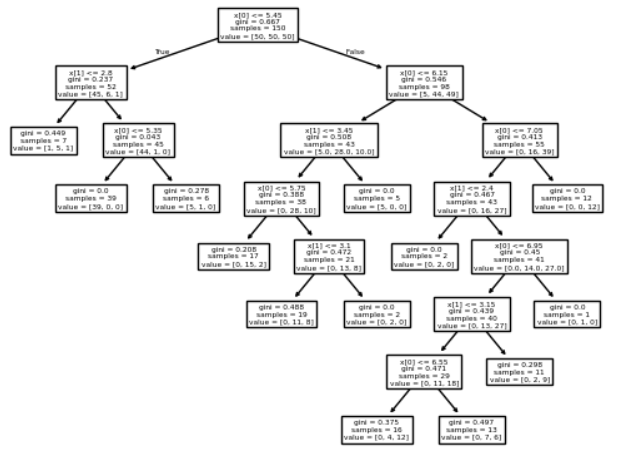
python 复制代码 
# 最小节点样本数
# 即决策树的叶子节点数不能低于***,低于这个数就要向上合并
clf = DecisionTreeClassifier(min_samples_split=5)
clf.fit(x, y)
decision_boundary_plot(x, y, clf)
plot_tree(clf)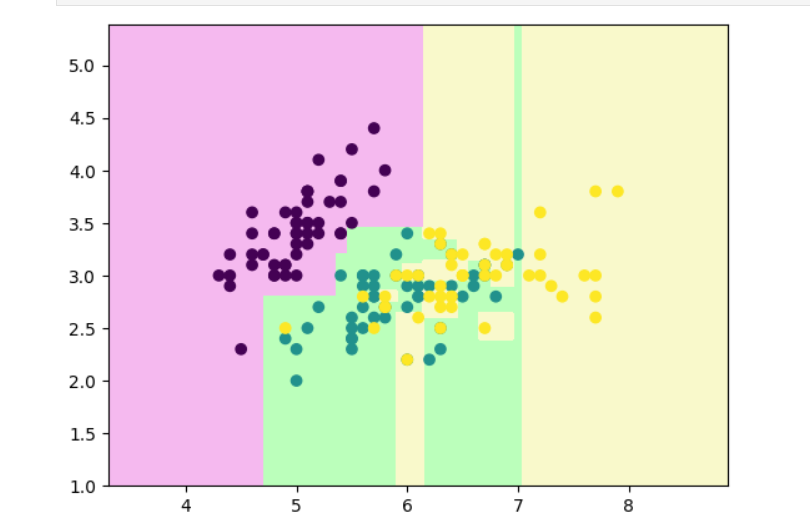
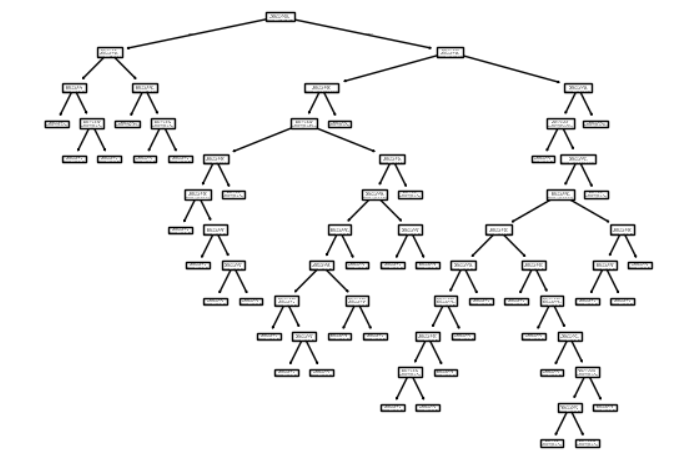
python 复制代码 
# 叶子节点样本的最小权重
# 此处是限制每个叶子节点的样本"权重占比"不能低于整个样本总权重的 3%
clf = DecisionTreeClassifier(min_weight_fraction_leaf=0.03)
clf.fit(x, y)
decision_boundary_plot(x, y, clf)
plot_tree(clf)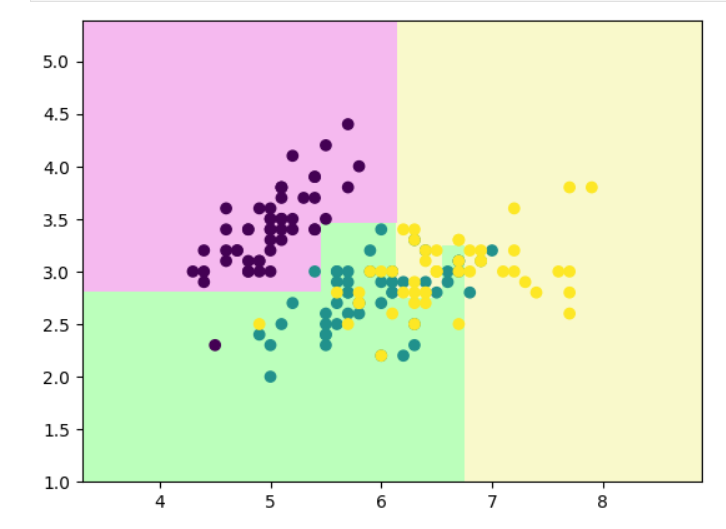

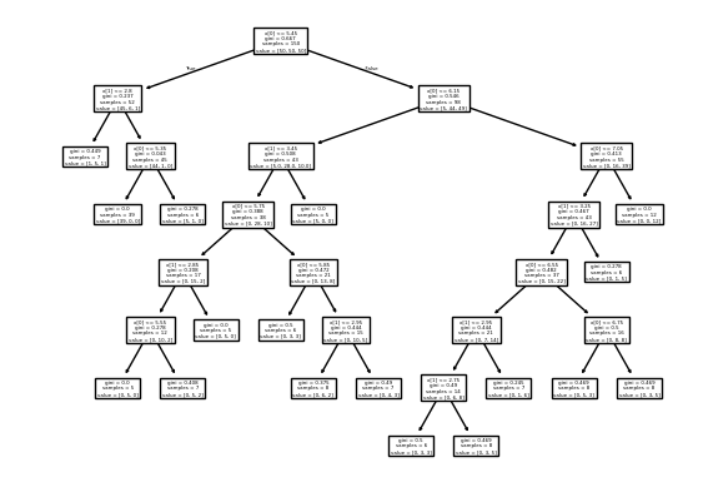
决策树回归任务代码实现

决策树如何回归？

由于相似的输入必然产生相似的输出

取节点平均值

项目 分类树（DecisionTreeClassifier） 回归树（DecisionTreeRegressor）
输出 类别（离散值） 数值（连续值）
划分指标 基尼系数 (Gini) 或 信息熵 (Entropy) 均方误差 (MSE) 或 平均绝对误差 (MAE)
叶节点值 投票最多的类别 样本目标值的平均数
应用场景 鸢尾花分类、垃圾邮件识别等 房价预测、温度估计、股票回归等
python 复制代码 
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import r2_score

# =========================
# 1) 数据集（改为加州房价）
# =========================
cal = datasets.fetch_california_housing()
x = cal.data
y = cal.target
# 把数据随机分为训练集与测试集（默认 75% 训练，25% 测试）
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=233)

# =========================
# 2) 基础模型训练与评分
# =========================
reg = DecisionTreeRegressor()
reg.fit(x_train, y_train)

# 返回 决定系数 R²
print(reg.score(x_test, y_test))
print(reg.score(x_train, y_train))

输出：
0.5824658488130179
1.0
python 复制代码 
# =========================
# 3) 学习曲线（随训练样本数变化）
# =========================
plt.rcParams["figure.figsize"] = (12, 8)
max_depth = [2, 5, 10, 20]

for i, depth in enumerate(max_depth):
    reg = DecisionTreeRegressor(max_depth=depth), 
    reg = DecisionTreeRegressor(max_depth=depth)

    train_error = []
    test_error  = []

    for k in range(len(x_train)):
        reg.fit(x_train[:k+1], y_train[:k+1])

        y_train_pred = reg.predict(x_train[:k + 1])
        train_error.append(r2_score(y_train[:k + 1], y_train_pred))

        y_test_pred = reg.predict(x_test)
        test_error.append(r2_score(y_test, y_test_pred))

    plt.subplot(2, 2, i + 1)
    plt.ylim(0, 1.1)
    plt.title("Depth: {0}".format(depth))
    plt.plot([k + 1 for k in range(len(x_train))], train_error, label='train')
    plt.plot([k + 1 for k in range(len(x_train))], test_error,  label='test')
    plt.legend()

plt.tight_layout()
plt.show()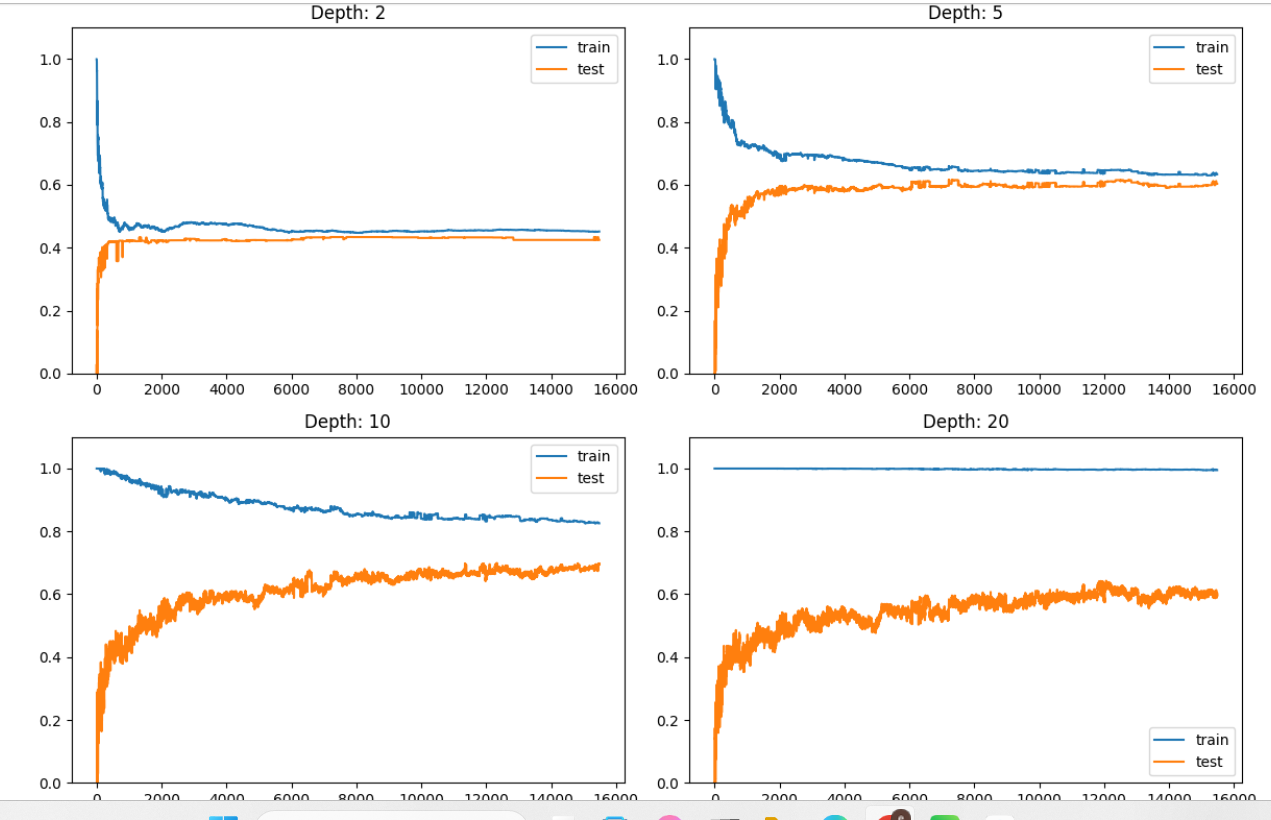

分析：

子图 max_depth 特征 模型表现解释
左上 2 训练和测试曲线都较平稳且收敛 模型较简单 → 偏差大、方差小，欠拟合。
右上 5 训练得分略高，测试得分上升后趋稳 模型复杂度适中 → 泛化较好。
左下 10 训练分数高，测试分数开始上升后停在0.6左右 模型开始过拟合。
右下 20 训练分数几乎为1.0，测试分数约0.6 模型完全记住训练数据 → 过拟合严重。

总体规律总结：

指标 随深度变化的趋势
训练集 R² 随着深度增加而持续升高，趋近 1.0
测试集 R² 先升后降，通常在中等深度（如 5~10）处达到最优
泛化能力 在 depth=5~10 时最好，过小欠拟合、过大过拟合
python 复制代码 
# =========================
# 4) 网格搜索，找到最佳的超参数
# =========================
params = {
    'max_depth': [n for n in range(2, 15)],
    'min_samples_leaf': [sn for sn in range(3, 20)],
}

grid = GridSearchCV(
    estimator = DecisionTreeRegressor(),
    param_grid = params,
    n_jobs = -1
)

grid.fit(x_train, y_train)

print(grid.best_params_)
print(grid.best_score_)

reg = grid.best_estimator_
print(reg.score(x_test, y_test))

输出：
{'max_depth': 14, 'min_samples_leaf': 16}
0.7310066772774355
0.7284985242273161

分析：

  • 最优超参
    {'max_depth': 14, 'min_samples_leaf': 16}
    含义：允许树最深到 14 层 ，但每个叶子至少要有 16 个样本 。尽管深度看起来偏大，但配合较大的 min_samples_leaf 会强制合并小叶子、起到"平滑/正则化"的作用，从而抑制过拟合 。这也解释了为什么之前 max_depth=20 会过拟合，而现在加了叶子最小样本数后能泛化得更稳。
  • 交叉验证成绩（内部验证）
    best_score_ = 0.7310
    这是在训练集上做 K 折（默认 5 折）交叉验证得到的平均 R²。它代表你在看不见的折上（相当于验证集）的期望表现。
  • 独立测试集成绩
    reg.score(x_test, y_test) = 0.7285
    与 best_score_ 非常接近（0.731 vs 0.728），说明CV 评估与真正泛化误差吻合 ，配置稳定，没有明显的过拟合或数据泄漏。对加州房价这种噪声较多、非线性的回归问题来说，~0.73 的 R²已经是相当合理的树模型表现。

决策树优缺点和适用条件

  1. 优点

符合人类直观思维

可解释性强

能够处理数值型数据和分类型数据

能够处理多输出问题

  1. 缺点

容易产生过拟合

决策边界只能是水平或竖直方向

不稳定，数据的微小变化可能生成完全不同的树

举个例子：

python 复制代码 
# 正常情况下生成决策树
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris

iris = load_iris()
X = iris.data[:,2:]
y = iris.target

from sklearn.tree import DecisionTreeClassifier

dt_clf = DecisionTreeClassifier(max_depth = 2,random_state=666)
dt_clf.fit(X, y)

def decision_boundary_plot(X, y, clf):
    axis_x1_min, axis_x1_max = X[:,0].min() - 1, X[:,0].max() + 1
    axis_x2_min, axis_x2_max = X[:,1].min() - 1, X[:,1].max() + 1
    
    x1, x2 = np.meshgrid( np.arange(axis_x1_min,axis_x1_max, 0.01) , np.arange(axis_x2_min,axis_x2_max, 0.01))
    z = clf.predict(np.c_[x1.ravel(),x2.ravel()])
    z = z.reshape(x1.shape)
    
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#F5B9EF','#BBFFBB','#F9F9CB'])

    plt.contourf(x1, x2, z, cmap=custom_cmap)
    plt.scatter(X[:,0], X[:,1], c=y)
    plt.show()

decision_boundary_plot(X, y, dt_clf)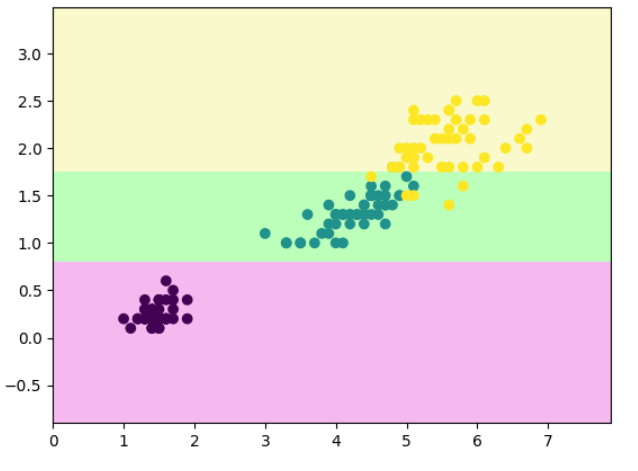
python 复制代码 
# 把第 131 个样本（X[130]）的两个特征改成 [6, 0.5]，然后重新训练模型。
X[130] = [6, 0.5]
dt_clf.fit(X, y)
decision_boundary_plot(X, y, dt_clf)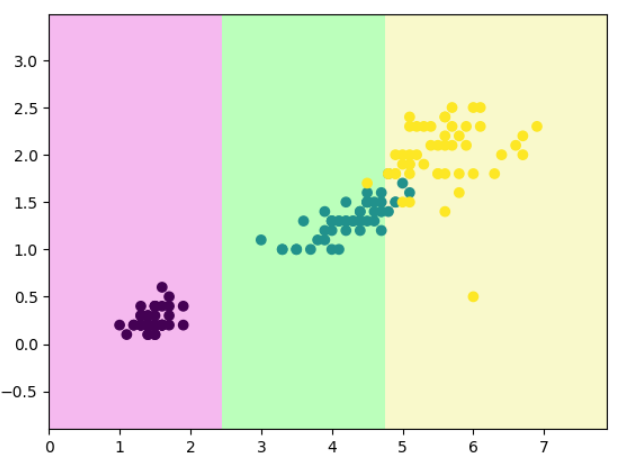

结果说明：

决策树对输入数据非常敏感（sensitive）：

  • 一点小的数据偏差、异常值、噪声都能改变划分结果；
  • 深度越大，敏感性越强；
  • 因此通常会配合参数控制（如 max_depth, min_samples_leaf, min_samples_split）或剪枝（ccp_alpha）防止过拟合。

5、神经网络

在神经网络中，每一次失败（预测错误）都会促进下一次成功（预测更准）------这正是"失败乃成功之母"的数学体现

俗语的含义 神经网络中的对应机制
"失败" 模型预测错误，损失函数（Loss）很大
"从失败中学习" 计算误差（Loss）并反向传播
"吸取教训" 调整权重（Weights）以减少错误
"慢慢变得更好" 不断迭代训练，Loss 越来越小
"成功" 模型收敛，预测准确率高

神经网络是什么？

倒过来发现就是多叉决策树

再换个角度理解：

神经网络核心思想和原理

神经网络的核心思想是"用大量简单的线性单元，通过非线性组合，自动逼近复杂函数"。

也就是说：

  • 每个神经元只会做一件简单的事：线性加权 + 非线性变换；
  • 把很多神经元分层组合起来时，它就能表达非常复杂的模式（比如图像识别、语言理解、天气预测等）

这就是所谓的 "复杂性来自简单性"

神经元模型：

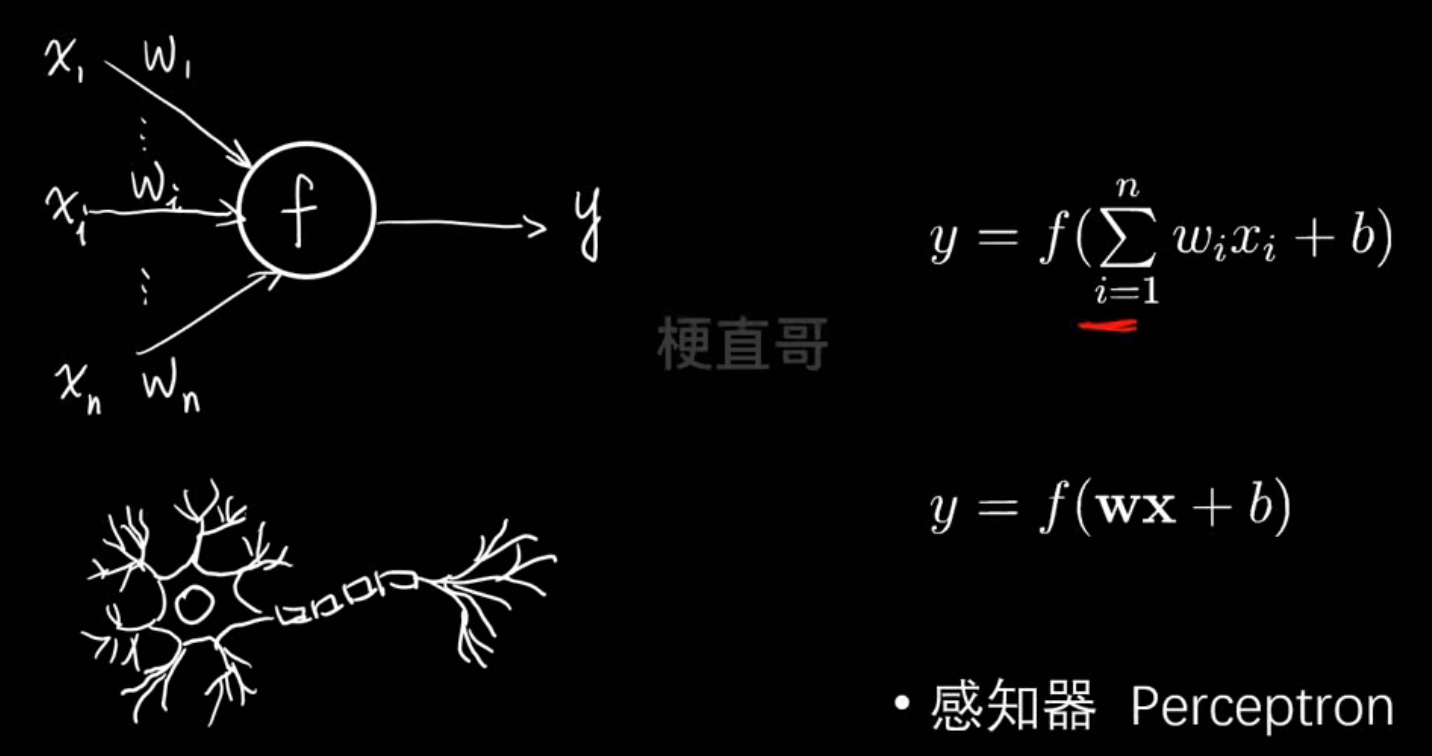
神经网络结构：

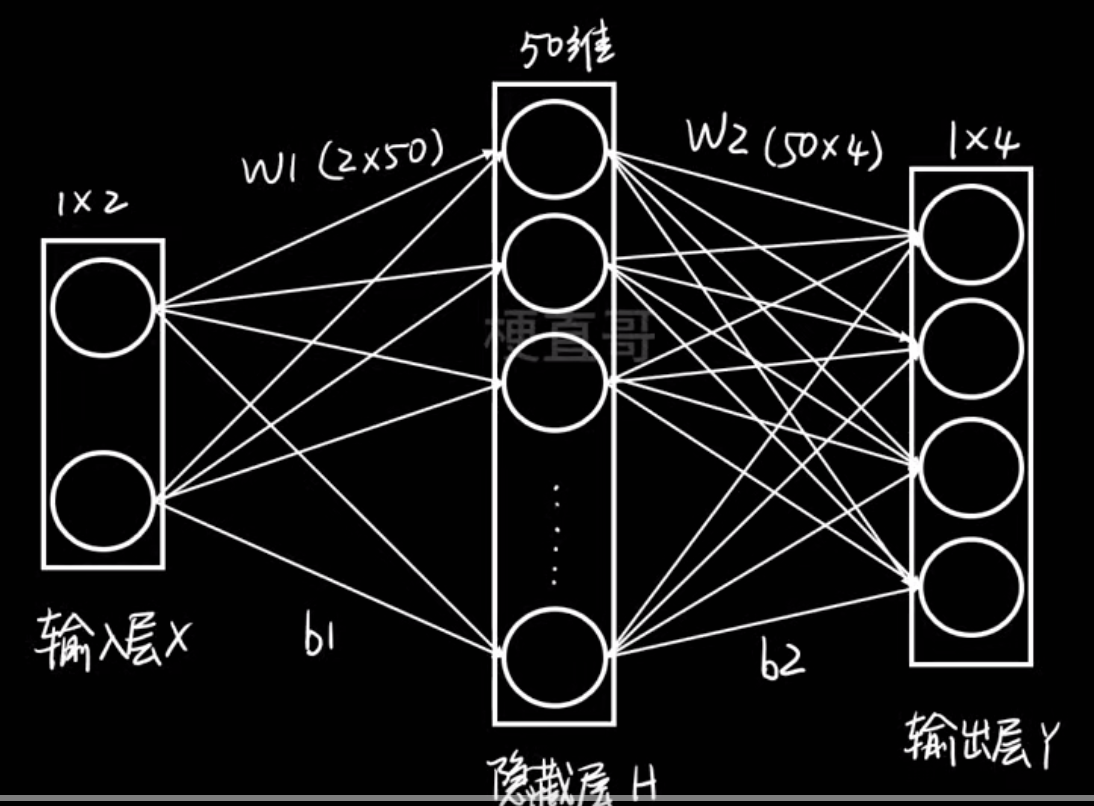
在这个例子中：

  • 输入：2个特征（x₁, x₂）
  • 经过隐藏层 50 个神经元的非线性组合
  • 输出：4个结果（比如分类为A、B、C、D的概率）

也就是说，它在学习一个从二维特征 → 四维输出 的复杂非线性映射。

激活函数层：

本质就是把线性的变成非线性的

有什么用：

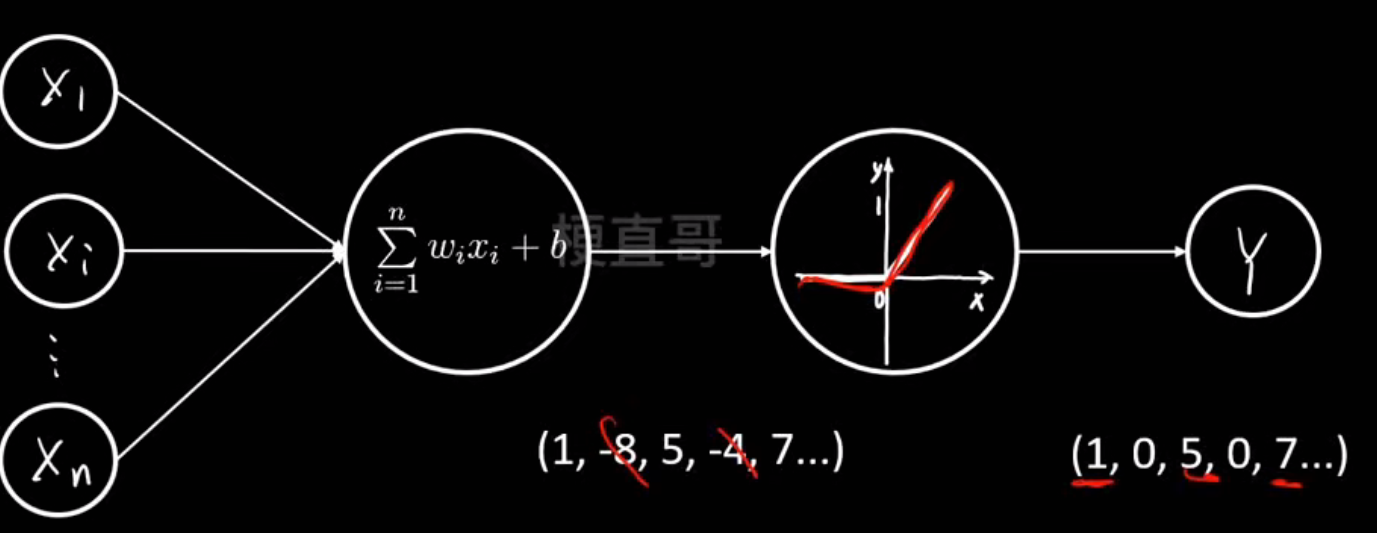
输出层：

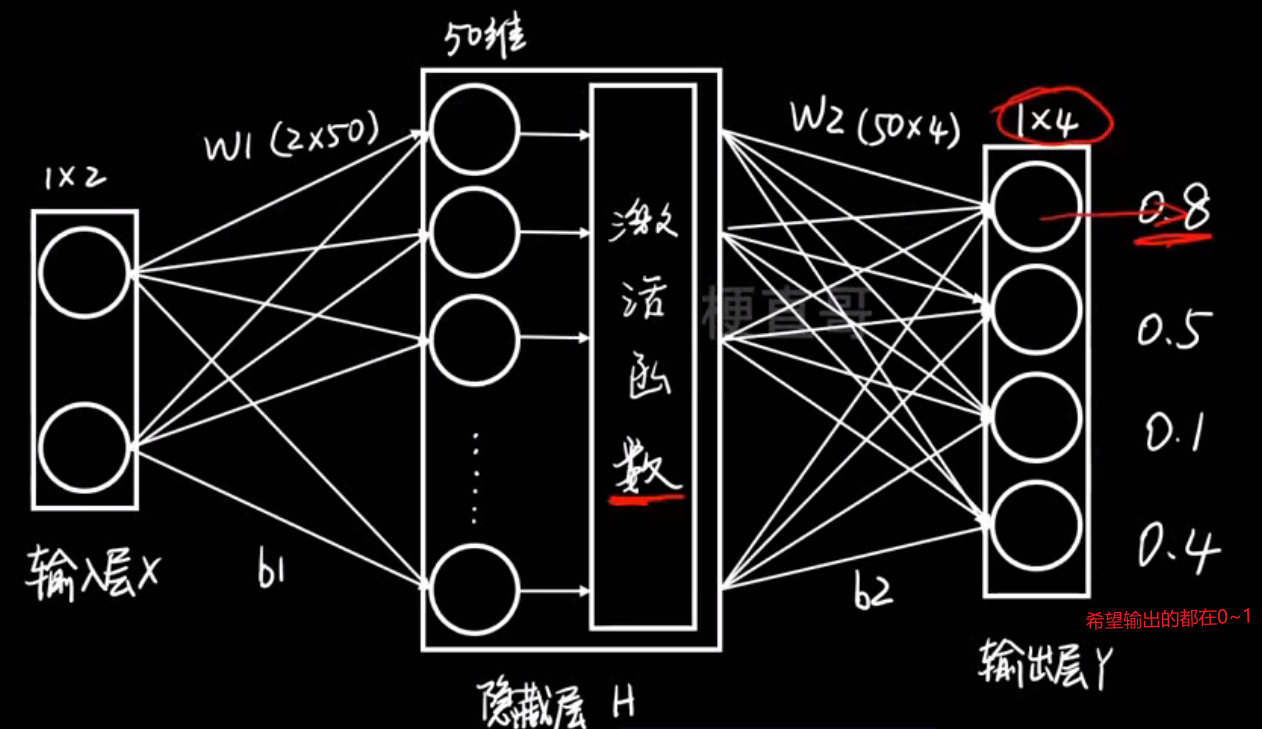
softmax层：

把一组任意实数（可以正、可以负）变换成一个概率分布

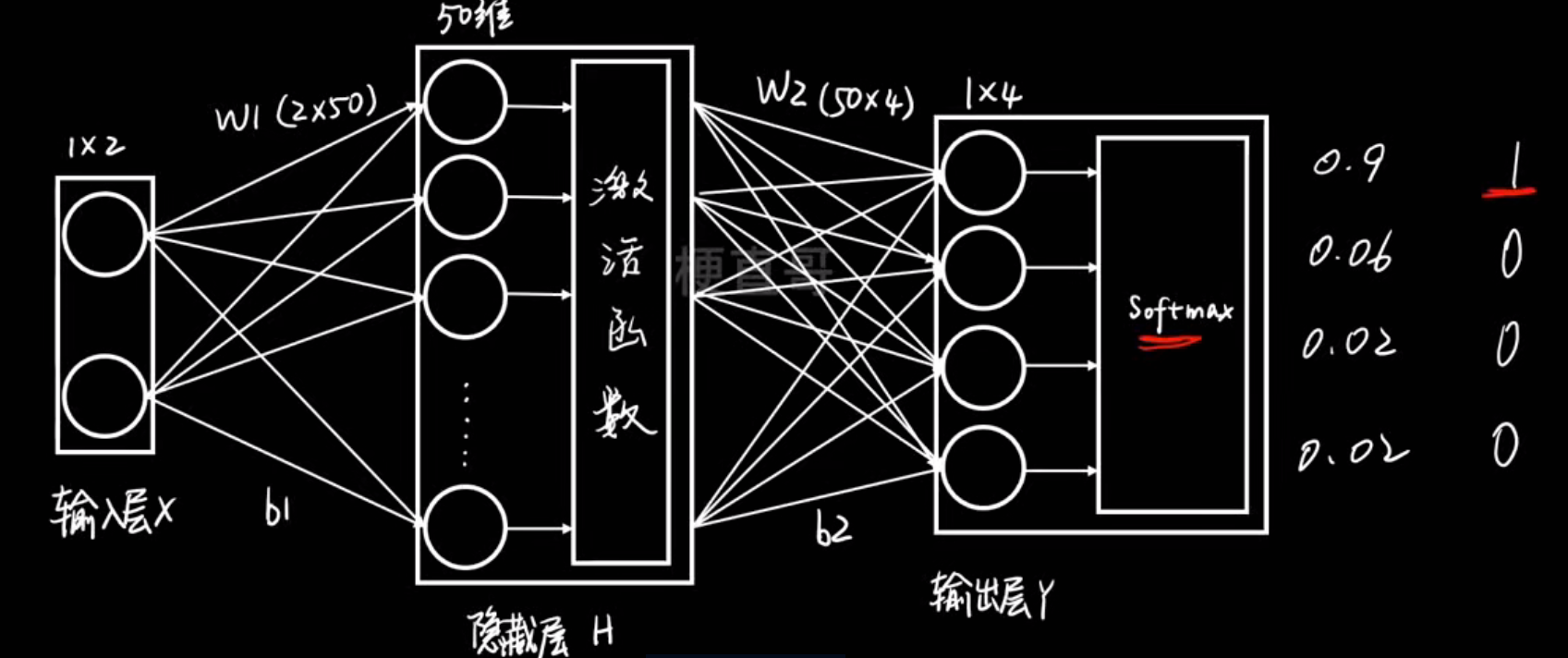
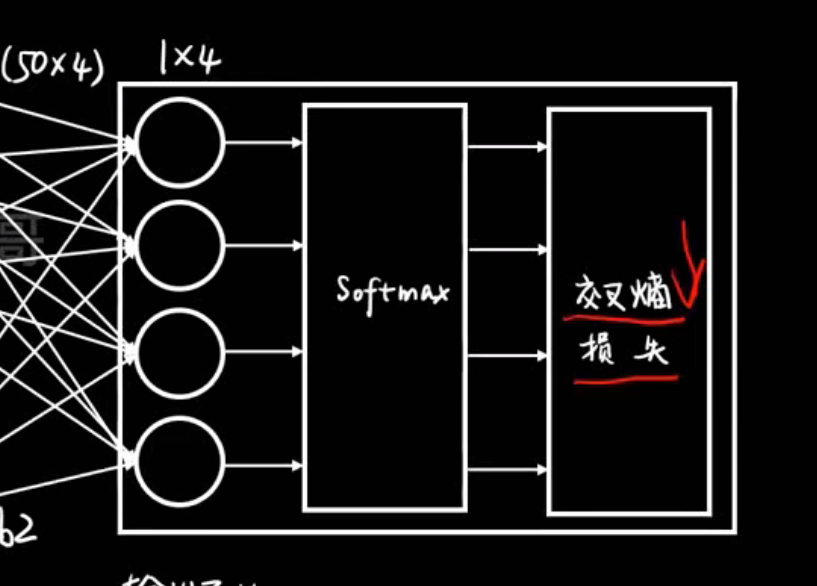
反向传播：

阶段 名称 方向 作用
1 前向传播 (Forward Propagation) 从输入到输出 算出预测结果和损失
2 反向传播 (Backpropagation) 从输出到输入 算出每个参数的"责任"，并更新它
  • 计算损失对输出层每个权重的影响；
  • 再计算损失对隐藏层权重的影响；
  • 一层层往回传播"误差信号"。

激活函数

为什么要使用激活函数？

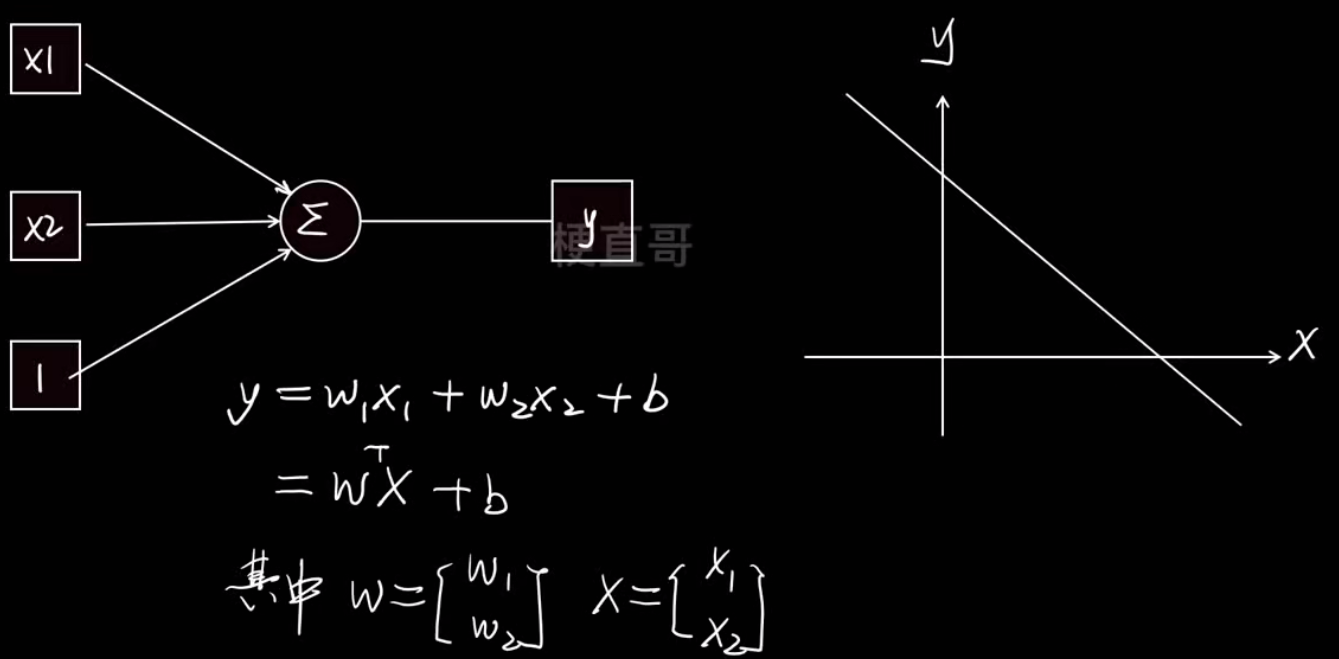
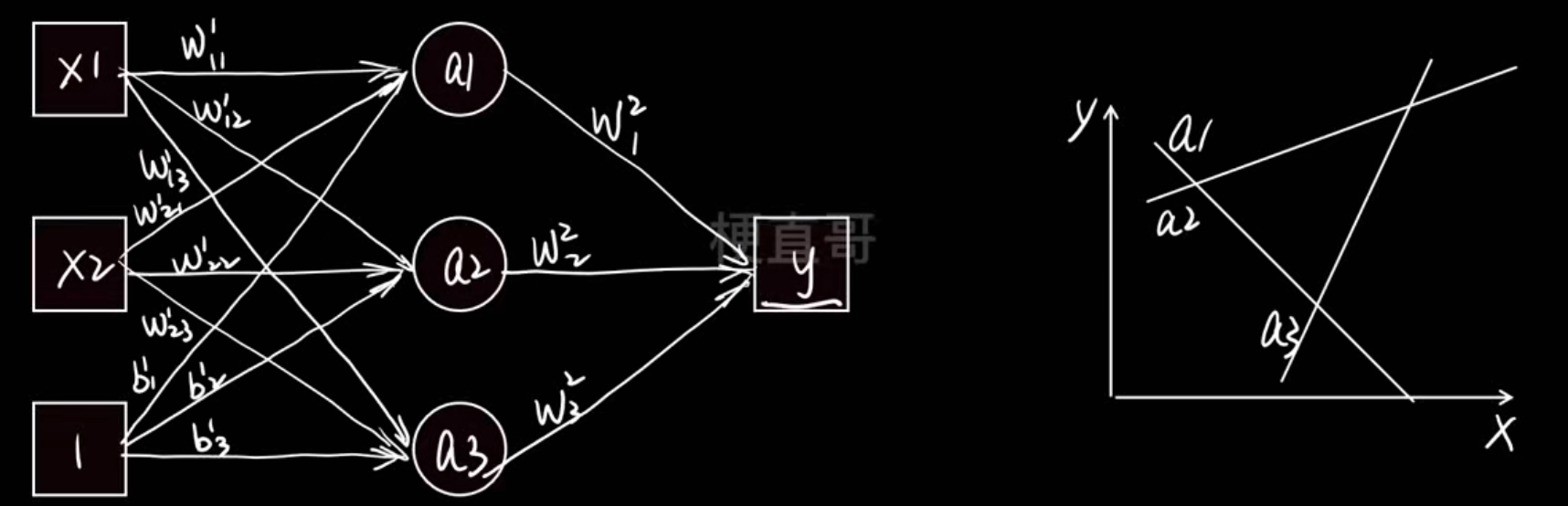
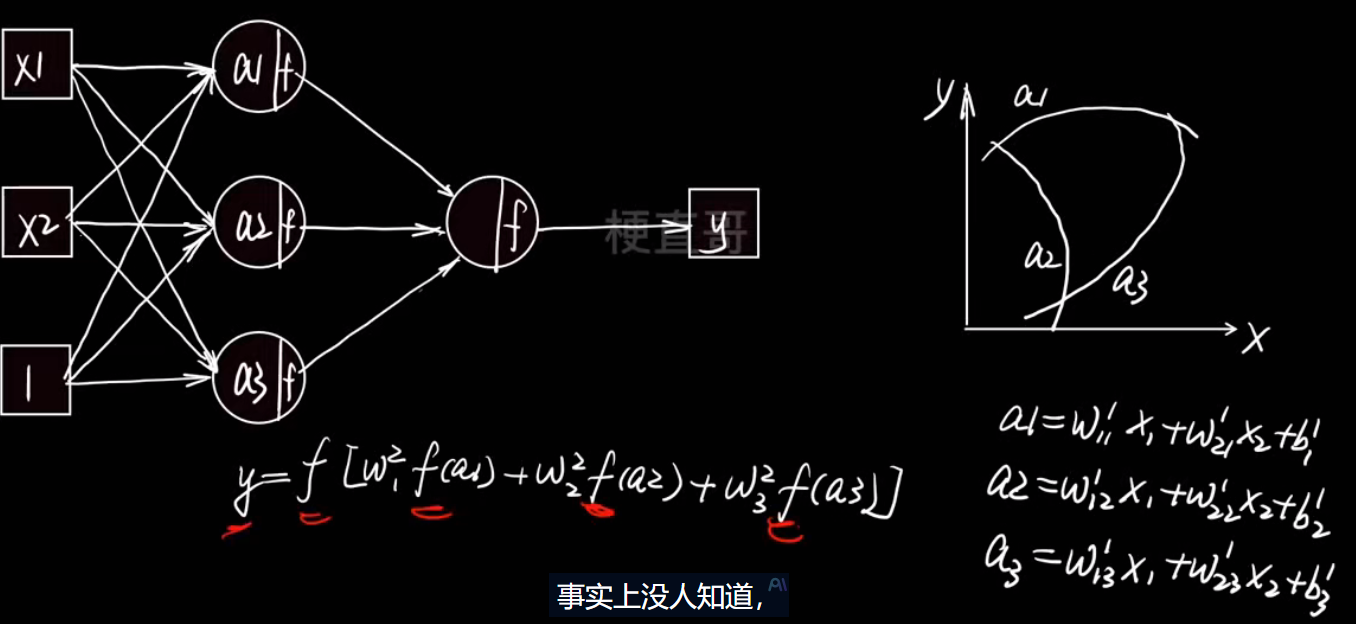
右边的图非常关键：

  • 横轴是输入 x，
  • 纵轴是输出 y，
  • 三条小曲线 a1,a2,a3是三组不同的线性组合（即三条直线）。

如果没有激活函数，这三条只是直线，无法表达复杂关系。

就成了多条非线性函数的加权叠加。

结果：这些"弯弯曲曲"的函数可以拼出任意复杂的形状（曲线、曲面、波动......）。这就是神经网络能拟合任意函数的关键

不管堆多少层，没有激活函数的网络永远只能画出直线，无法拟合曲线

最经典的sigmoid函数：

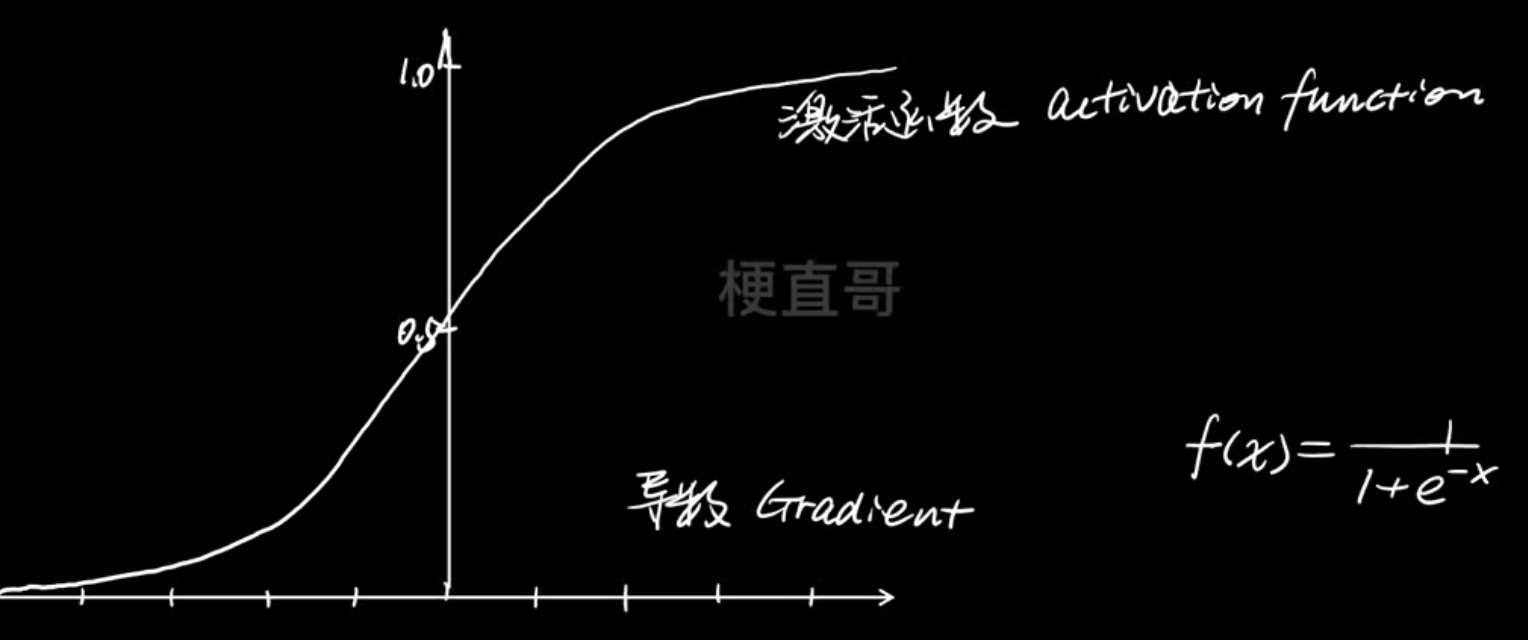
但这个函数会引起梯度消失的问题，且函数输出以0.5为中心而不是以0为中心，这会降低权重更新的效率

于是改进提出了Tanh函数---- 以 0 为中心，范围 (-1,1)

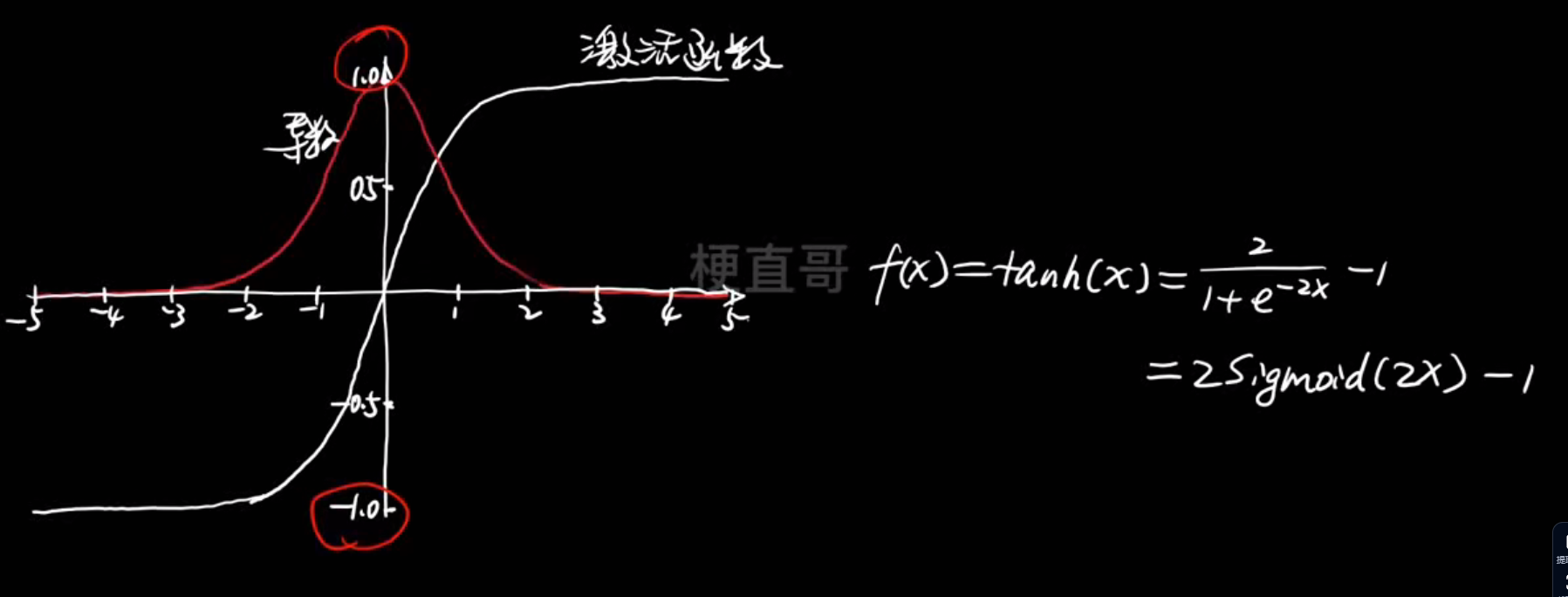
但是还是会有梯度消失，于是提出了 ReLU函数 ----- 线性区域梯度恒定，0~∞

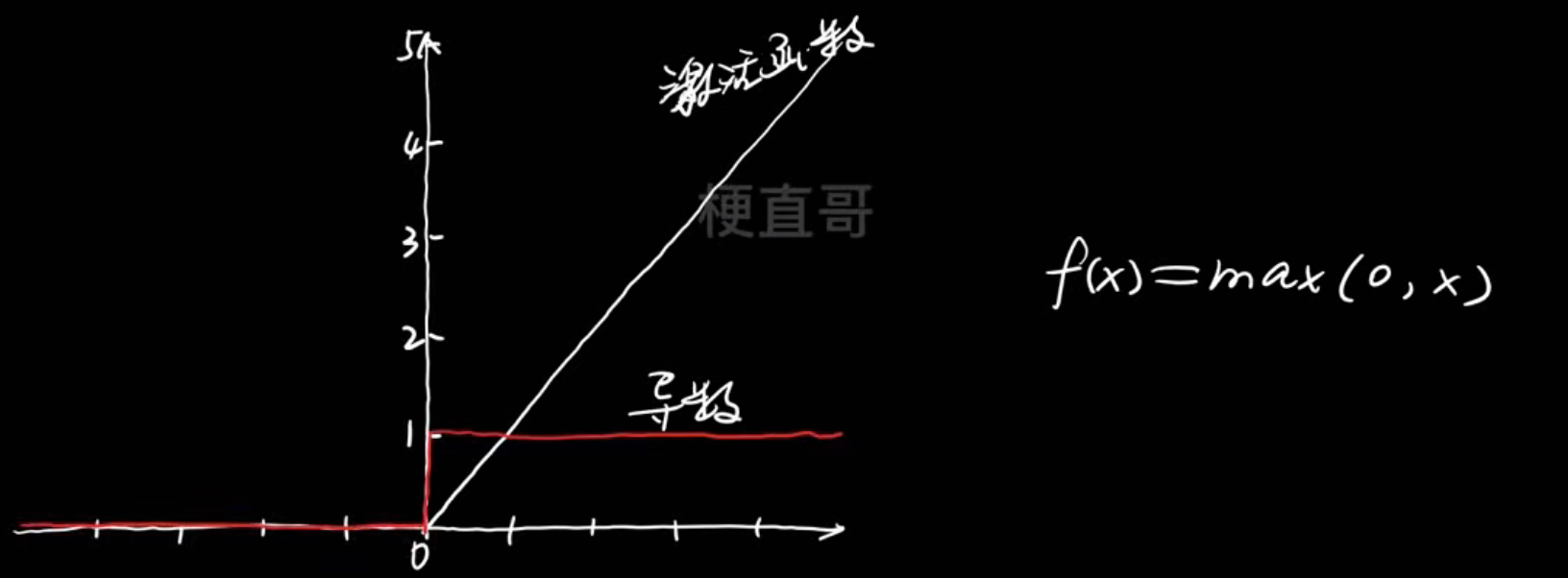
但是这个会导致神经元死亡问题，即输入为负的神经元的激活值总是为0

ReLU函数的各种变体：

还有一种经典的叫Softmax函数

如何选择激活函数？

  • 不要把各种激活函数串联在一个网络使用
  • 如果用ReLU,小心设置学习率
  • 尽量不用sigmoid，可以试试tanh

正向传播与反向传播

模型学习的过程

  1. 正向传播（Forward）
    输入数据从头到尾通过网络，产生预测结果。
  2. 计算损失（Loss）
    计算预测结果和真实结果之间的差距。
  3. 反向传播（Backward）
    计算每个参数对误差的"责任"，求出梯度。
  4. 参数更新（Gradient Descent）
    根据梯度方向调整权重，减少下一次的错误。
python 复制代码 
           ┌────────────────────────────┐
           │  正向传播：预测 → 计算损失   │
           │  输入 x → 输出 ŷ → Loss L   │
           └────────────────────────────┘
                         ↓
           ┌────────────────────────────┐
           │  反向传播：计算梯度 → 更新参数│
           │  误差反传 → 修正权重 W,b     │
           └────────────────────────────┘

反向传播原理----最小化损失函数

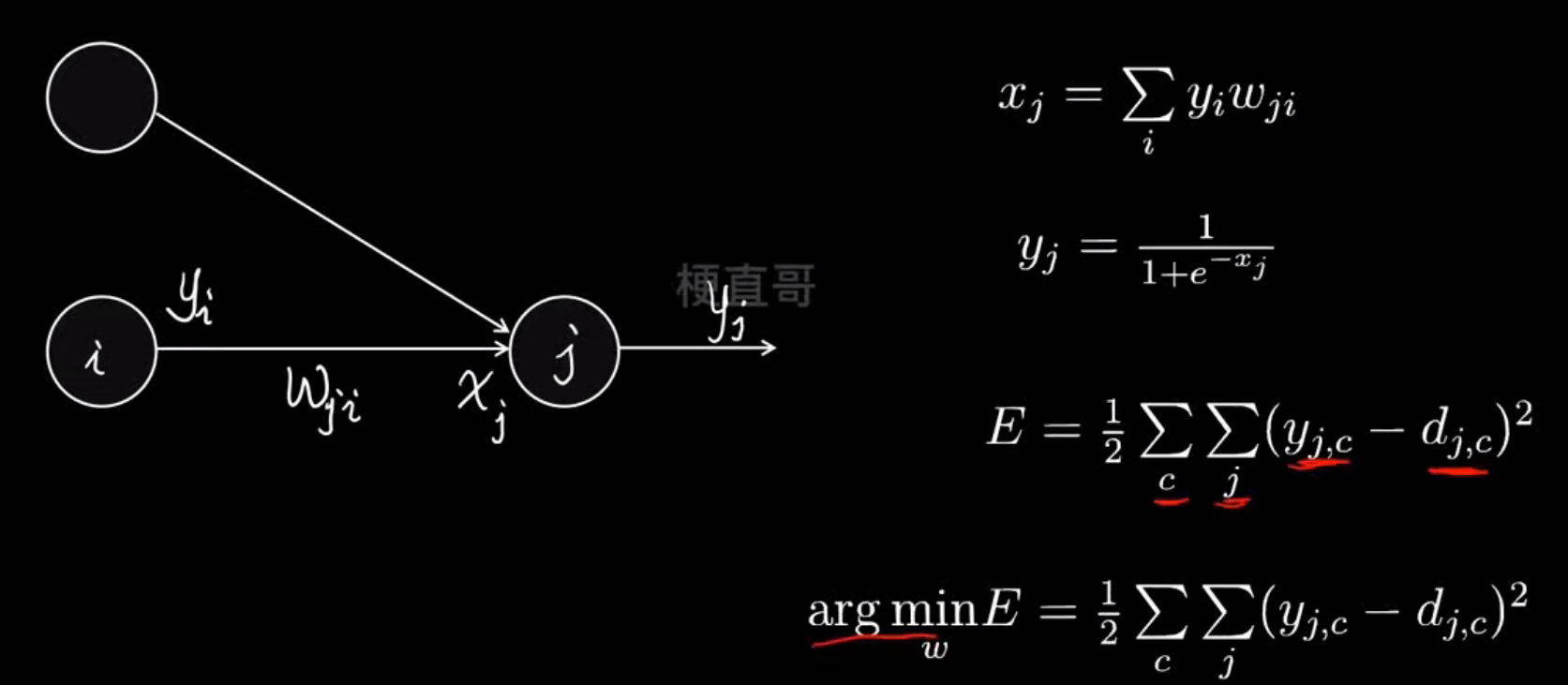
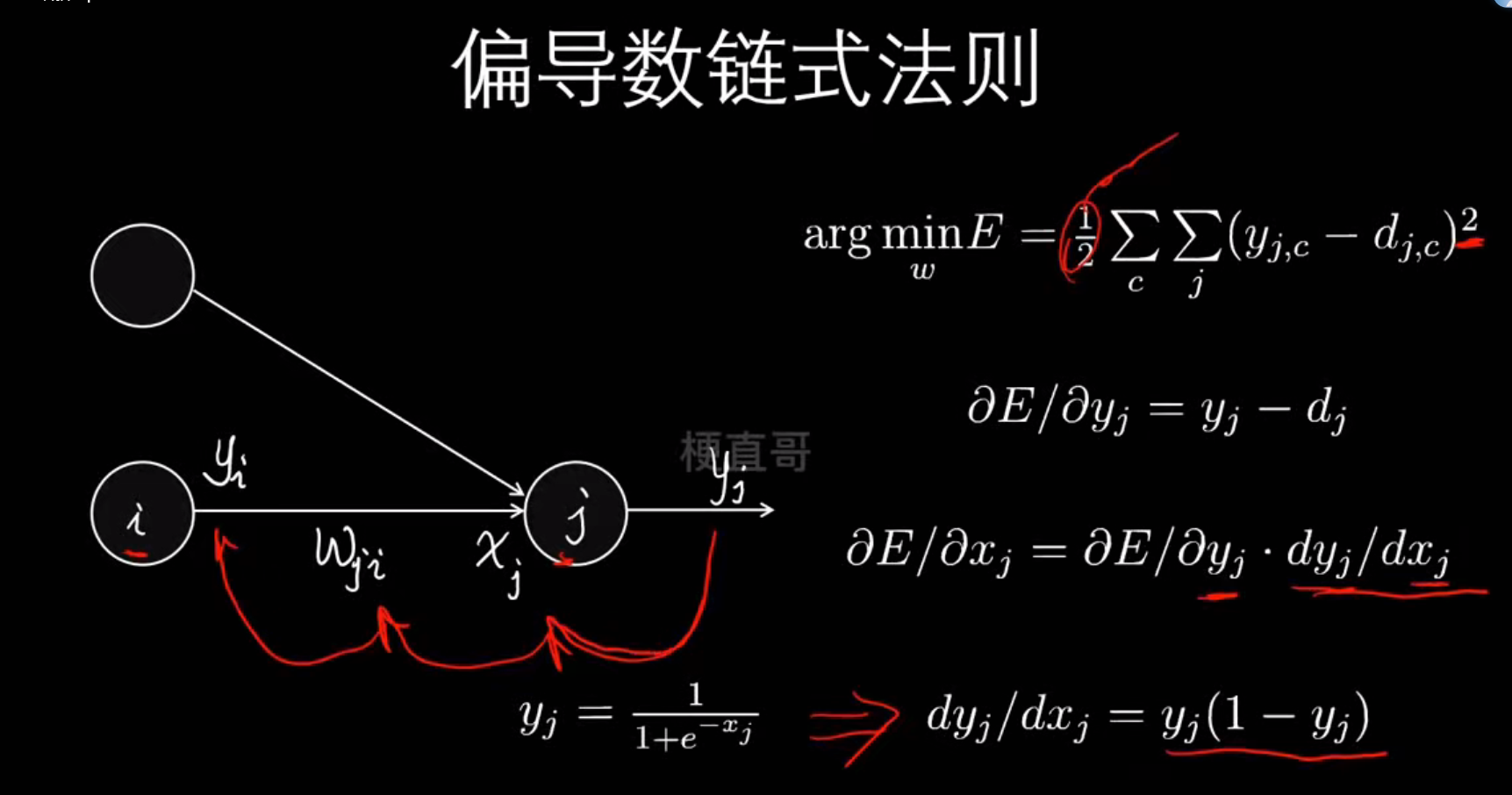
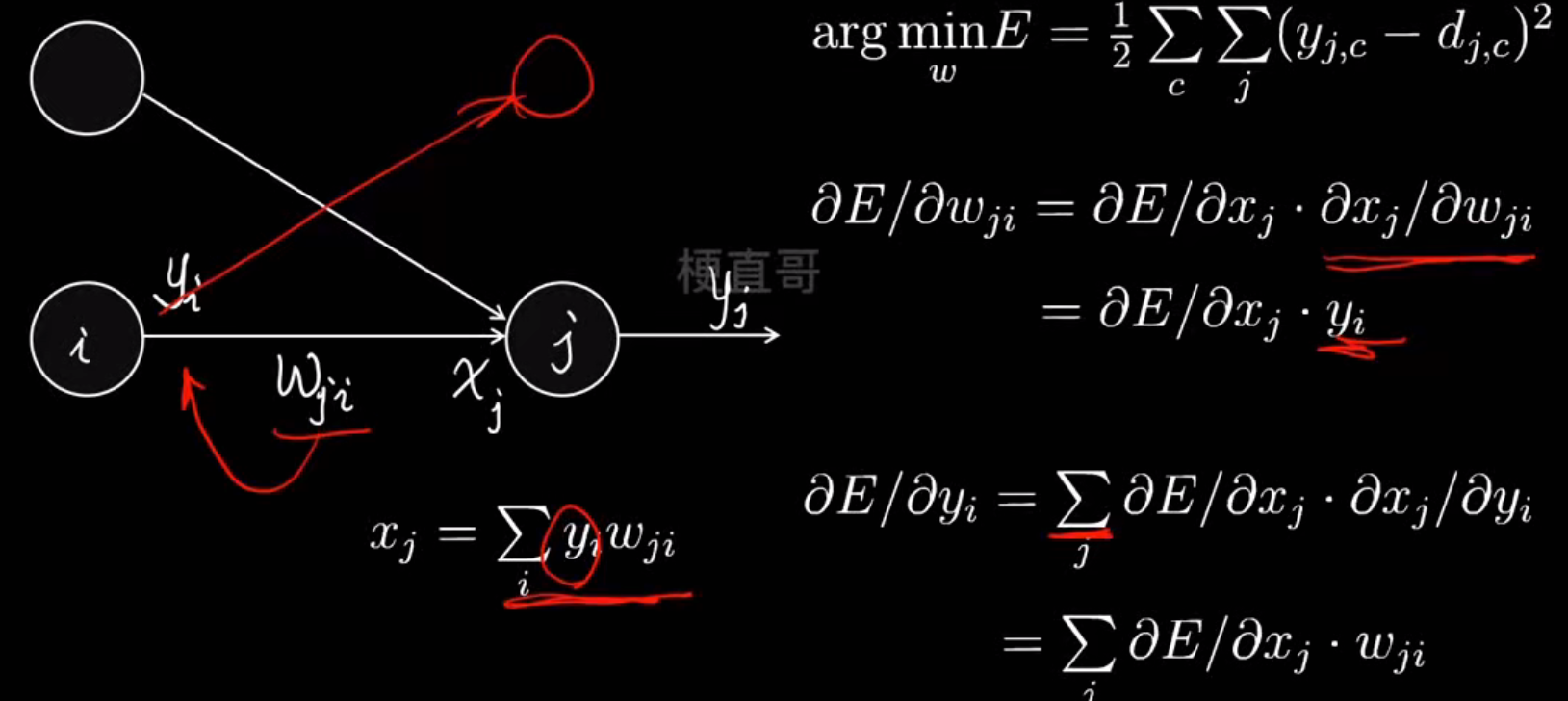
梯度下降优化算法

优化原则：

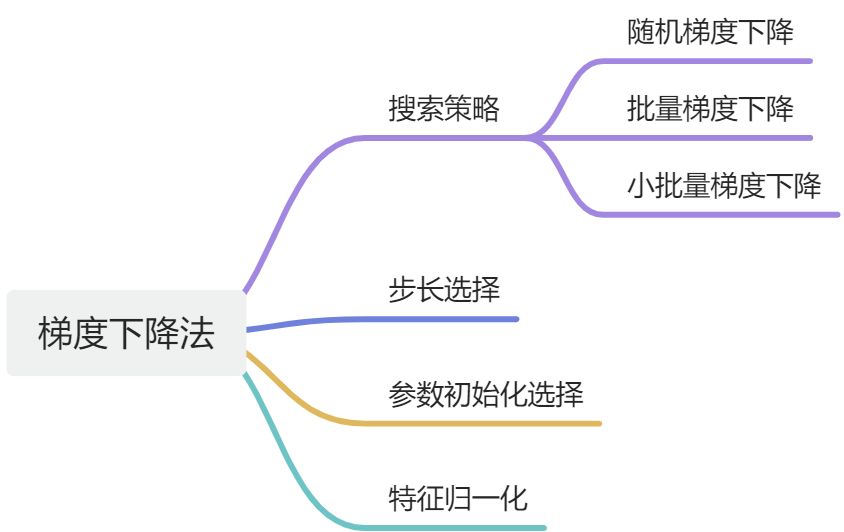
搜索策略

  1. 批量梯度下降（Batch Gradient Descent）

原理：每次迭代使用 所有训练样本 来计算一次总体梯度：

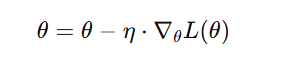
特点：

  • 精确方向：每次更新都沿着最陡的下降方向。
  • 计算量大：需要遍历整个数据集才能更新一次。
  • 内存开销大：难以在大规模数据上运行。

举例：

假如你有 10 万张图片，每次都要把 10 万张都过一遍再更新一次参数，非常慢。

适用场景：

  • 小数据集
  • 对精确收敛要求高的任务（如线性回归理论分析）
  1. 随机梯度下降（Stochastic Gradient Descent, SGD）

原理：每次只使用一个样本来计算梯度并更新参数：

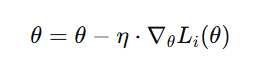
特点：

  • 更新频繁：几乎每看一个样本就更新一次。
  • 速度快，但波动大：因为单个样本的梯度噪声大，损失曲线会"抖动"。
  • 能跳出局部最优：噪声反而能帮助网络越过"局部坑"。

适用场景

  • 在线学习（数据流式到达）
  • 大数据集，快速粗略优化
  • 深度学习早期探索阶段
  1. 小批量梯度下降（Mini-Batch Gradient Descent）

原理：每次使用一个小批量样本（mini-batch）（比如32或64个）计算平均梯度：

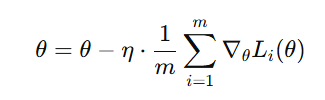
特点：

  • 折中方案：兼顾稳定性和效率
  • 计算并行化：适合GPU并行加速
  • 波动适中：在梯度噪声和收敛稳定性之间取得平衡
  • 是现代深度学习的默认选择

适用场景

  • 几乎所有深度学习任务
  • 大规模神经网络（CNN、Transformer等）
  1. 三者比较总结表
策略 每次使用样本数 更新频率 收敛速度 稳定性 是否支持GPU并行 应用场景
批量梯度下降 全部样本 低 慢 稳定 弱 小数据集，理论推导
随机梯度下降 1 个样本 高 快但震荡 不稳定 强 流式学习，大数据
小批量梯度下降 一小批（如32） 中 快 稳定 强 主流深度学习训练

标配Adam算法

  1. 可视化理解（直观比喻）

假设你要从山顶下山到谷底：

  • 批量下降：每次先测整个山的地形，一次走一步，稳但慢。
  • 随机下降：闭着眼凭感觉走，每次只看脚下，快但容易乱走。
  • 小批量下降：一小队人拿着局部地图，一边走一边修正方向，稳且高效。

步长选择

步长就是下降速度，大小要多次尝试，不能太大也不能太小

公式：

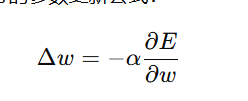
符号 含义
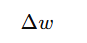参数更新量（每次权重要改多少）
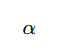学习率（learning rate，又叫"步长"）
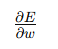误差函数对参数的偏导（梯度）
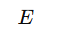损失函数（Loss Function）

梯度告诉我们"该往哪走"，而学习率 α 决定了"每一步走多远"。

  • 如果 α 太大 → 一步跨太远，可能"越过山谷"，导致发散。
  • 如果 α 太小 → 一步太短，收敛非常慢，甚至陷入局部震荡。

参数初始值的选择

初始值就是下山的起始点，初始值不同最小值也可能不同

多次尝试选择损失函数最小的

特征归一化

神经网络在训练时通过梯度下降 更新参数

如果不同层的特征分布波动很大，模型会出现：

  • 梯度爆炸 / 梯度消失
  • 训练不稳定、收敛慢
  • 激活函数进入饱和区（尤其是sigmoid/tanh）

归一化的目标是：保持每层输入和输出的分布稳定，让网络更快、更稳地学习

这在深层网络中尤为关键，因为层与层之间的信号传播容易"漂移"，即所谓的 Internal Covariate Shift（内部协变量偏移）

神经网络简单代码实现

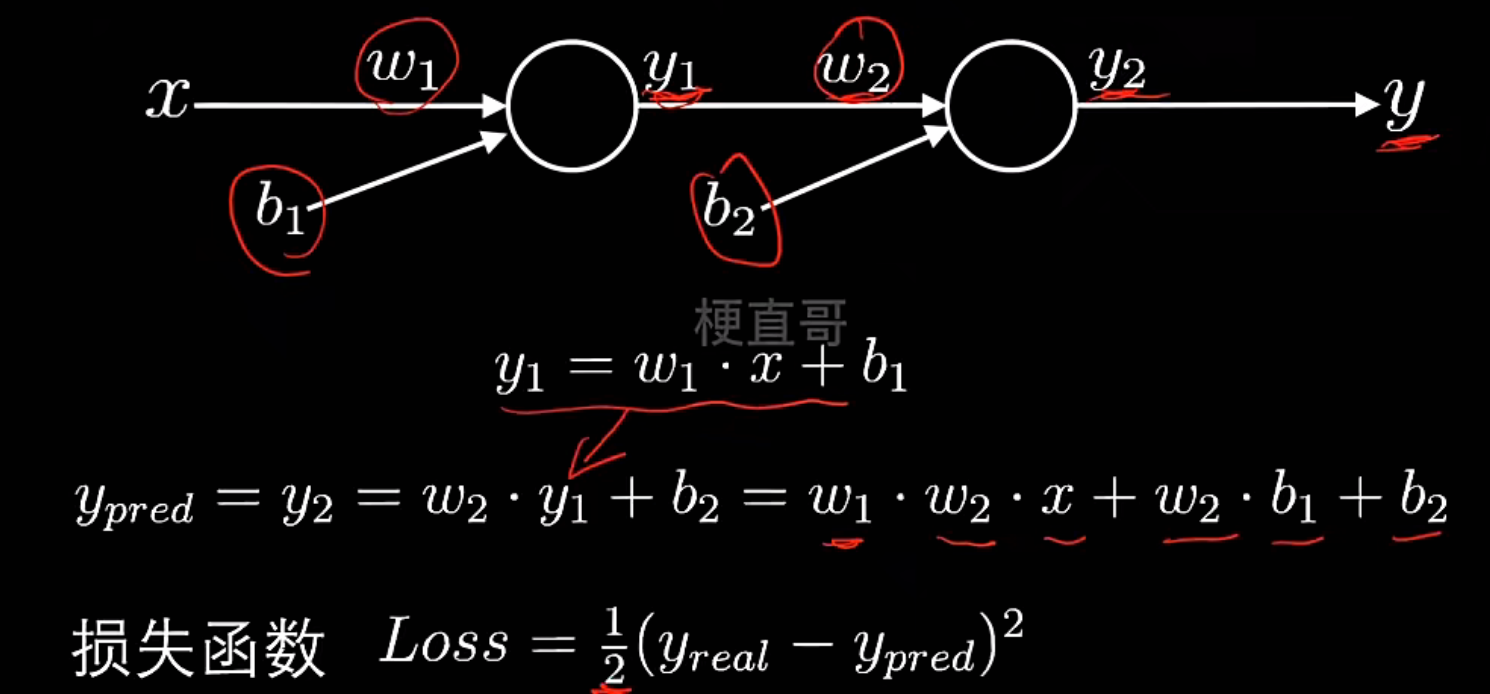
符号 含义
x 输入
w₁, b₁ 第一层的权重、偏置
y₁ 第一层输出
w₂, b₂ 第二层的权重、偏置
y₂（或ŷ, y_pred） 网络预测输出
y_real 真实标签
E 损失（loss）或误差函数

简单神经网络---正向传播：

简单神经网络---反向传播：

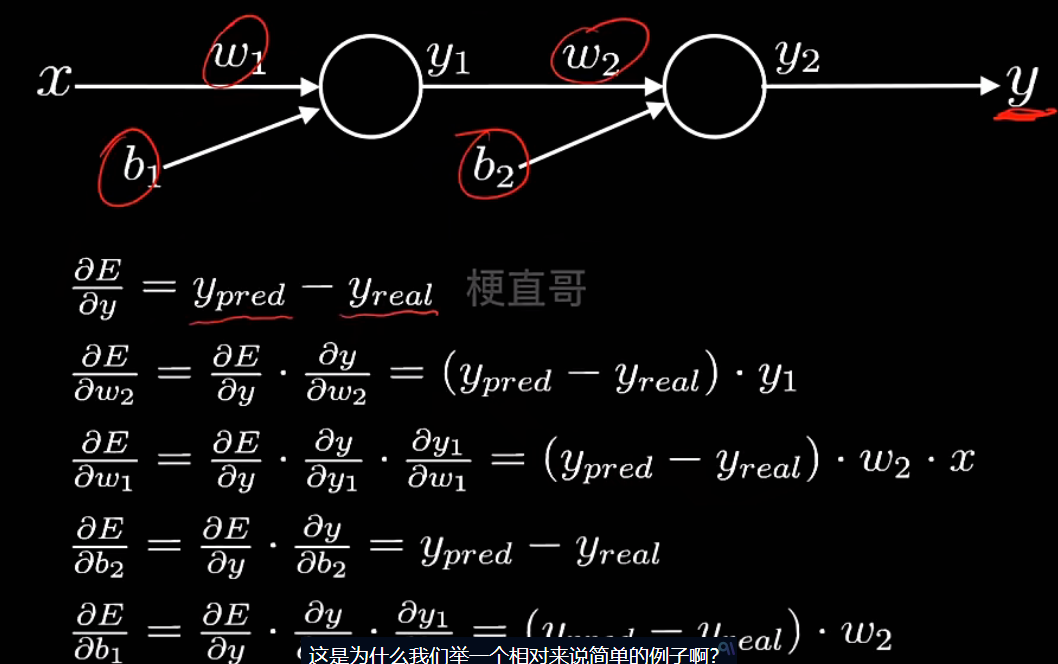
代码实现：

最简单的神经网络结构：

python 复制代码 
输入 x  →  隐藏层 y1 → 输出层 y_pred
python 复制代码 
# 数据集
import numpy as np
import matplotlib.pyplot as plt

w,b=1.8,2.5
np.random.seed(0)
x=np.random.rand(100)*4-2
noise=np.random.randn(100)/3
y=w*x+b+noise

x=x.reshape(-1,1)
x.shape,y.shape

输出：
((100, 1), (100,))
python 复制代码 
# 绘制图像
plt.scatter(x,y)
plt.show()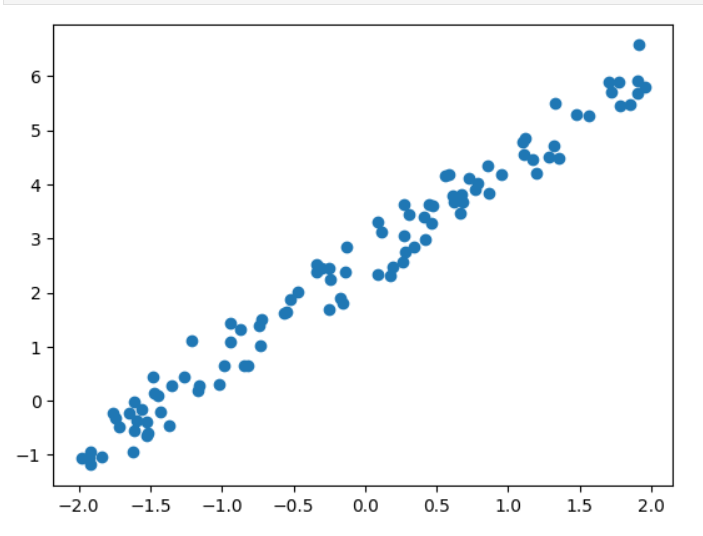
python 复制代码 
# sklearn中的神经网络
from sklearn.neural_network import MLPRegressor
reg= MLPRegressor(
    hidden_layer_sizes=(1,),  #带权重的输出层的权重
    activation='identity',   #不加激活函数
    learning_rate_init=0.01,  #初始学习率
    random_state=233  
)
reg.fit(x,y)
reg.score(x,y)  #查看拟合效果

输出：
0.974674992013746
python 复制代码 
y_pred=reg.predict(x)
plt.scatter(x,y)
plt.plot(x,y_pred,c='red')
plt.show()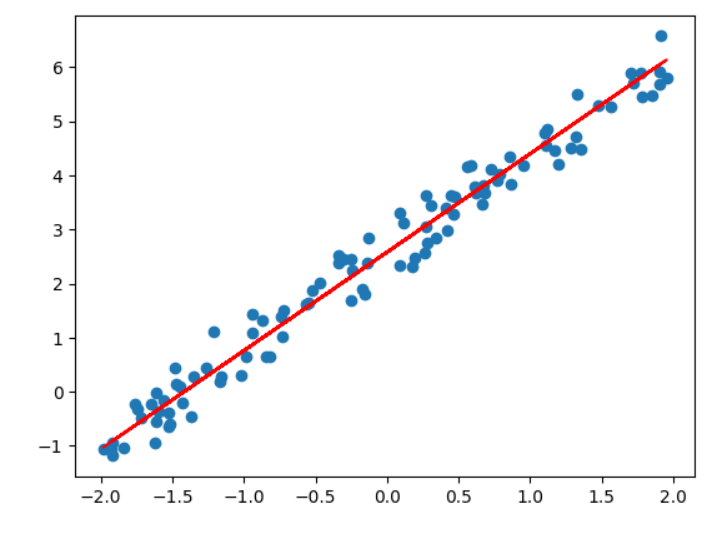
python 复制代码 
# 查看权重和偏置
w1,w2=np.array(reg.coefs_).reshape(-1)
b1,b2=np.array(reg.intercepts_).reshape(-1)
print(w1,w2,b1,b2)

输出：
-2.0230772887975506 -0.8994147672147477 0.20843202333485145 2.7673419504355397
python 复制代码 
# 结果就是前面定义的w=1.8,b=2.5,可能有一点偏差
w1 * w2, w2 * b1 + b2

输出：
(np.float64(1.8195855887612917), np.float64(2.5798751106877256))

反向传播：

python 复制代码 
# 反向传播权重更新
# 生成4个符合标准正态分布 N(0,1) 的数
w1,w2,b1,b2=np.random.randn(4)
w1,w2,b1,b2
输出：
(np.float64(-0.35399391125348395),
 np.float64(-1.3749512934180188),
 np.float64(-0.6436184028328905),
 np.float64(-2.2234031522244266))


y_real=y.reshape(-1,1)
lr=0.01
python 复制代码 
# 进行100次迭代训练，每次计算"前向传播 → 反向传播 → 参数更新"

for i in range(100):
    y1 = w1 * x + b1
    y_pred = w2 * y1 + b2
    loss = ((y_real - y_pred) ** 2) / 2
    
    dy = y_pred - y_real
    dy1 = dy * w2
    
    dw1 = np.mean(x * dy1)
    dw2 = np.mean(y1 * dy)
    db1 = np.mean(dy1)
    db2 = np.mean(dy)
    
    w1 -= lr * dw1
    w2 -= lr * dw2
    b1 -= lr * db1
    b2 -= lr * db2
    
print(w1, b1, w2, b2)

输出：
-0.7865961506365119 -1.8052603505178628 -2.281516347579787 -1.5557865752893039
python 复制代码 
w1 * w2, w2 * b1 + b2

输出：
(np.float64(1.7946319766205345), np.float64(2.562944426054817))
python 复制代码 
y_pred = w2 * (w1 * x + b1) + b2
plt.scatter(x, y)
plt.plot(x, y_pred, c = 'red')
plt.show()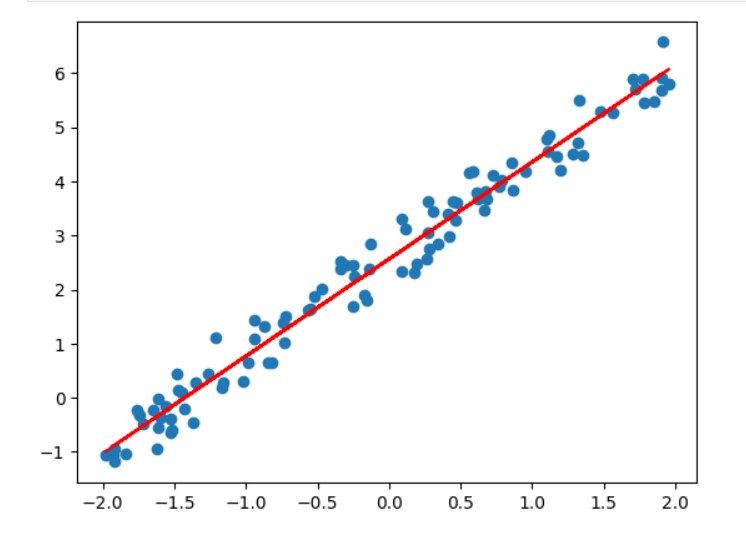

梯度消失和梯度爆炸

  1. 多层单神经元网络：

此网络有四个神经元串联四层：

python 复制代码 
x → [w₁,b₁,f] → y₁ → [w₂,b₂,f] → y₂ → [w₃,b₃,f] → y₃ → [w₄,b₄,f] → y₄ = ŷ
  1. 梯度消失：

梯度消失 ：深层网络中，梯度在反向传播时不断相乘变得越来越小，

导致前面的层几乎无法更新。

原因：激活函数导数（比如Sigmoid）太小。

解决：换激活函数（ReLU）、加归一化、加残差

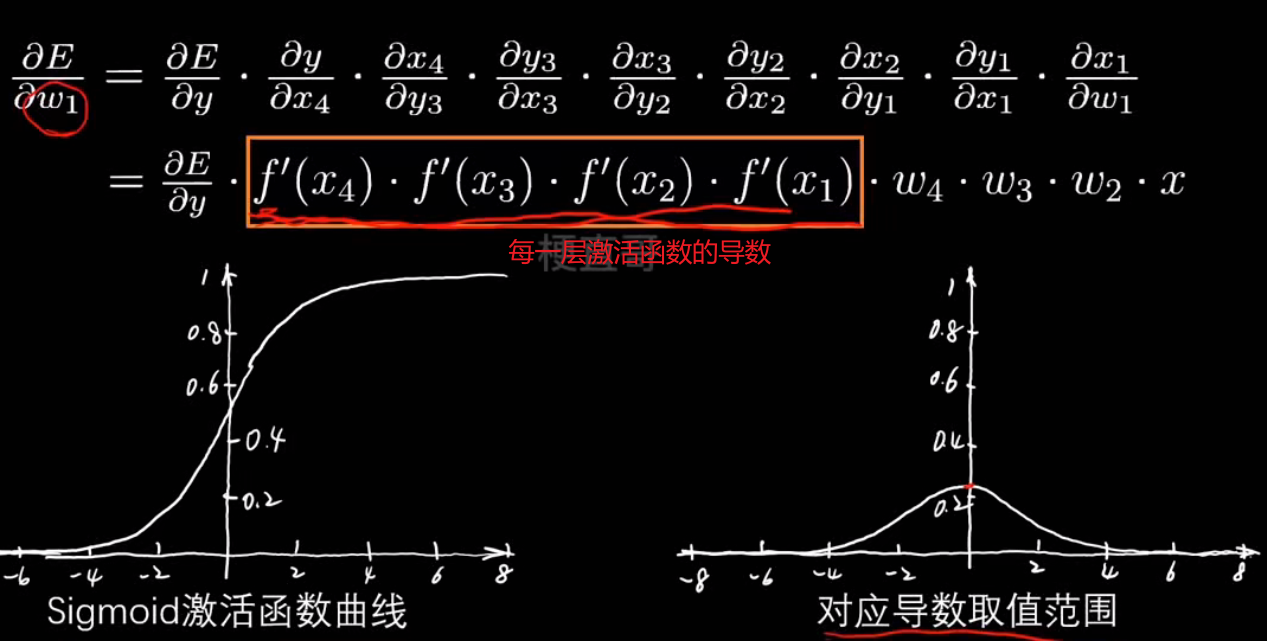
为什么叫梯度消失？

会导致网络退化

  1. 梯度爆炸

如果每一层的权重 wiw_iwi 或激活函数的导数 大于 1，这些数相乘后会迅速变得非常大------这就是梯度爆炸。

会导致网络不稳定

  1. 激活函数

更换更好的激活函数

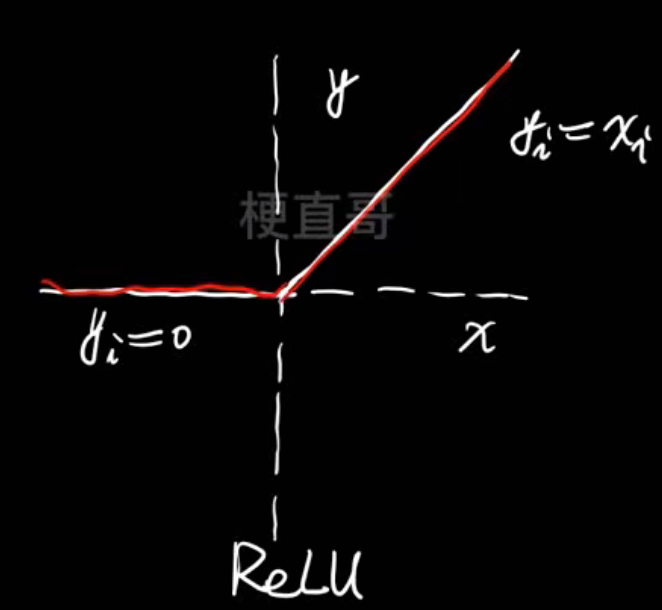
梯度剪切（对梯度爆炸有用）

改进网络结构

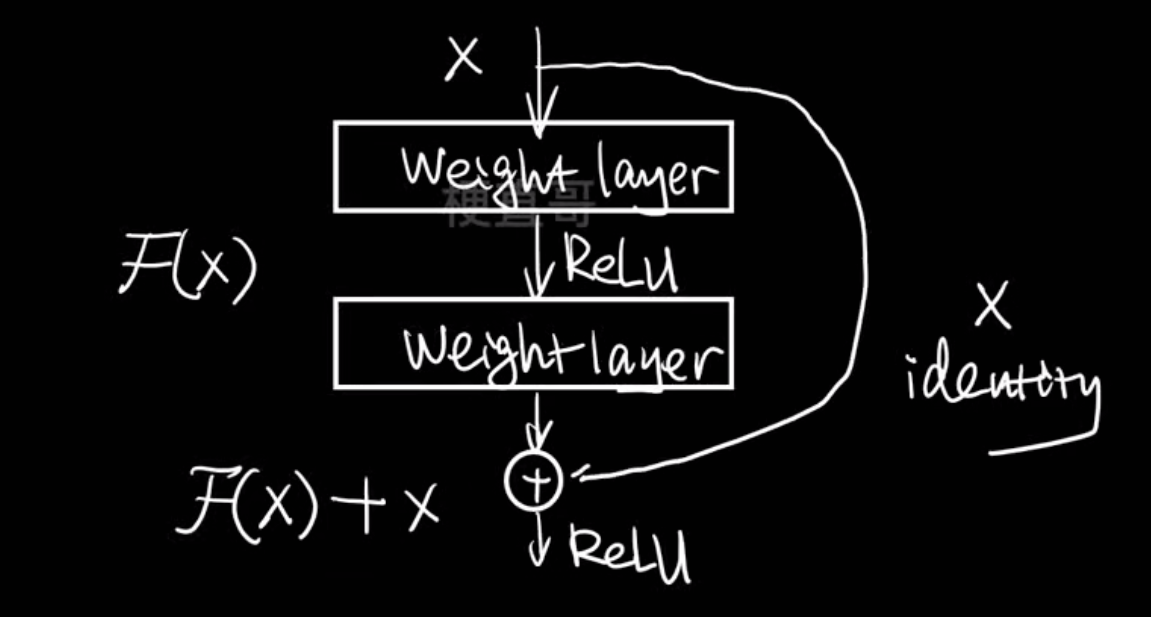
模型选择

什么是模型选择？

在相同数据集上比较不同模型（KNN、决策树、逻辑回归）的性能

选择的原则：

  • 模型效果
  • 运算速度
  • 算力要求
  • 可解释性

代码实现：

python 复制代码 
# 不同模型的比较
import numpy as np

from sklearn.neighbors import KNeighborsClassifier

from sklearn.tree import DecisionTreeClassifier

from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

from sklearn.model_selection import cross_val_score


def model_selection(x, y, cv):
    knn = KNeighborsClassifier(n_neighbors=3)
    dt = DecisionTreeClassifier(max_depth=5)
    lr = Pipeline([
        ('poly', PolynomialFeatures(degree=2)),
        ('log_reg', LogisticRegression(max_iter=500))
    ])

    print('knn_score: %.4f, dt_score: %.4f, lr_score: %.4f' % (
        np.mean(cross_val_score(knn, x, y, cv=cv)),
        np.mean(cross_val_score(dt, x, y, cv=cv)),
        np.mean(cross_val_score(lr, x, y, cv=cv))
    ))
    
dataset = datasets.load_iris()
x = dataset.data
y = dataset.target
cv = 5
model_selection(x, y, cv)r

输出：
knn_score: 0.9667, dt_score: 0.9533, lr_score: 0.9800

结果分析：

模型 平均准确率 解读
KNN 0.9667 高准确率，说明邻域投票效果好；Iris 是低维、类簇分明的数据，KNN表现优秀。
决策树 0.9533 稍低，可能因为 max_depth=5 限制了复杂度（过浅），或5折交叉验证中部分样本分界模糊。
逻辑回归（带二次项） 0.9800 表现最佳。二次多项式让线性模型具备非线性拟合能力，同时泛化良好。

在Iris数据集上，逻辑回归（多项式特征） > KNN > 决策树。这与数据特性高度吻合 ------ Iris 数据是近似线性可分的三分类问题

python 复制代码 
# 数据集从 Iris（鸢尾花） 换成了 Digits（手写数字识别）
dataset = datasets.load_digits()
x = dataset.data
y = dataset.target
cv = 5
model_selection(x, y, cv)

输出：
knn_score: 0.9666, dt_score: 0.6328, lr_score: 0.9405

根据结果分析：

在手写数字识别任务中：

  • KNN 表现最佳，因为"距离"能很好反映数字形状的相似性；
  • 逻辑回归（二次特征） 次之，泛化稳定；
  • 决策树（max_depth=5） 太浅，欠拟合严重；

调整决策树深度或引入更复杂模型（如随机森林、神经网络）后，准确率能轻松突破 0.95

python 复制代码 
# 使用神经网络模型
from sklearn.neural_network import MLPClassifier
nn = MLPClassifier(
    hidden_layer_sizes = (1,), 
    activation = 'identity', 
    learning_rate_init = 0.01, 
    random_state = 233
)
np.mean(cross_val_score(nn, x, y, cv = 5))

输出：
np.float64(0.42405756731662014)

结果分析：

参数 含义 实际效果
hidden_layer_sizes=(1,) 只有一层隐藏层，且只有 1个神经元 模型几乎没有非线性表示能力
activation='identity' 线性激活 (f(x)=x) 网络整体退化成一个线性模型（等价于线性回归/逻辑回归）
learning_rate_init=0.01 学习率 还可以接受
random_state=233 固定随机种子 确保结果可复现

只有 1 个神经元 + 线性激活函数，实际上相当于一个线性回归模型。 所以效果不佳

神经网络的模型选择:

python 复制代码 
nn = MLPClassifier(
    hidden_layer_sizes = (5,), 
    activation = 'identity', 
    learning_rate_init = 0.01, 
    random_state = 233
)
np.mean(cross_val_score(nn, x, y, cv = 5))
输出：
np.float64(0.8809300526152894)
python 复制代码 
nn = MLPClassifier(
    hidden_layer_sizes = (100,), 
    activation = 'identity', 
    learning_rate_init = 0.01, 
    random_state = 233
)
np.mean(cross_val_score(nn, x, y, cv = 5))

输出：
np.float64(0.9176539770968741)
python 复制代码 
nn = MLPClassifier(
    hidden_layer_sizes = (5,), 
    activation = 'relu', 
    learning_rate_init = 0.01, 
    random_state = 233
)
np.mean(cross_val_score(nn, x, y, cv = 5))

输出：
np.float64(0.3060631383472609)
python 复制代码 
nn = MLPClassifier(
    hidden_layer_sizes = (100,100), 
    activation = 'relu', 
    learning_rate_init = 0.01, 
    random_state = 233
)
np.mean(cross_val_score(nn, x, y, cv = 5))

输出：
np.float64(0.943237387805633)
python 复制代码 
nn = MLPClassifier(
    hidden_layer_sizes = (100,50,100), 
    activation = 'relu', 
    learning_rate_init = 0.01, 
    random_state = 233,
    solver='sgd'
)
np.mean(cross_val_score(nn, x, y, cv = 5))

输出：
np.float64(0.9443593314763232)
python 复制代码 
nn = MLPClassifier(
    hidden_layer_sizes = (100,50,100,100,50,100,100,50,100), 
    activation = 'relu', 
    learning_rate_init = 0.01, 
    random_state = 233
)
np.mean(cross_val_score(nn, x, y, cv = 5))

输出：
np.float64(0.8920628288455585)
网络结构 激活 学习率 优化器 准确率 问题 / 优点
(5,), identity 线性 0.01 Adam 0.88 欠拟合
(100,), identity 线性 0.01 Adam 0.92 接近线性上限
(5,), relu 非线性 0.01 Adam 0.31 不收敛
(100,100), relu 非线性 0.01 Adam 0.94 最佳区间
(100,50,100), relu 非线性 0.01 SGD 0.94 稳定泛化好
(100,...多层), relu 非线性 0.01 Adam 0.89 过深→梯度不稳
(100,50,100)+Scaler+LR=0.001 relu 0.001 Adam ⭐0.97~0.98 最优配置

神经网络优缺点和使用条件

优点：

  • 范围广
    • 问题
    • 数据类型
  • 效果好
    • 泛化能力强
    • 容错能力强
  • 性能好
    • 并行计算
    • GPU or TPU计算

缺点：

  • 训练难度大
  • 训练时间长
  • 黑盒不可解释

适用条件：

  • 数据规模庞大，人工提取特征困难
  • 无需解释，只要结果

6、支持向量机

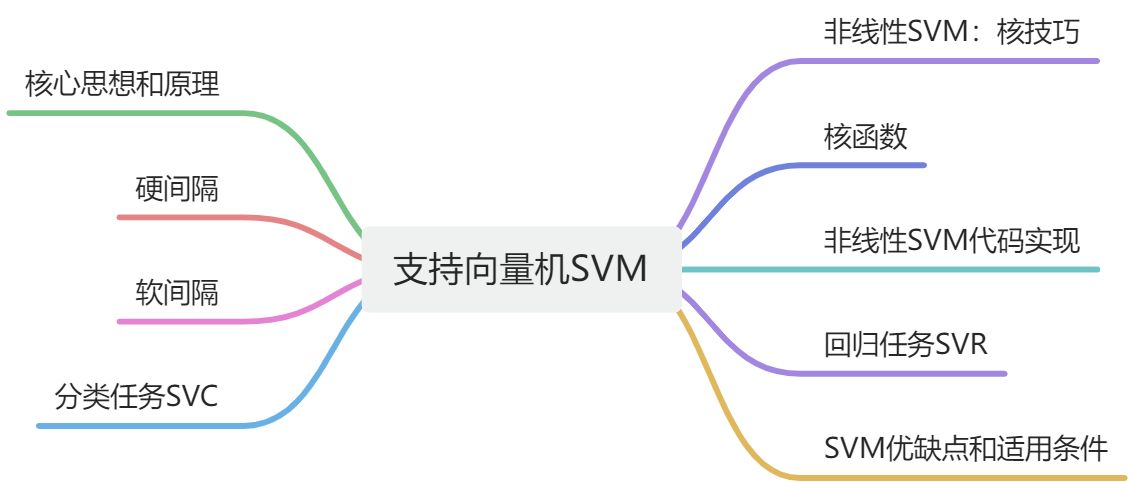
python 复制代码 
SVM（Support Vector Machine）支持向量机
│
├── 分类任务 → SVC（Support Vector Classification）
│      │
│      ├── LinearSVC（线性分类）
│      └── SVC(kernel='rbf'/'poly'/...)（非线性分类）
│
└── 回归任务 → SVR（Support Vector Regression）
       │
       ├── LinearSVR（线性回归）
       └── SVR(kernel='rbf'/'poly'/...)（非线性回归）

SVM核心思想和原理

假设我们有两类点（红色、蓝色）：

python 复制代码 
   蓝 ● ● ●
         ↑
         │   ←  这条线（或平面）就是分类边界
         │
   红 ● ● ●

SVM 的目标就是找到一个分割超平面（Hyperplane） ，把两类样本分开，同时尽可能让两边离这条线最远

核心思想：最大化间隔（margin）-------不仅要能分开数据，还要"分得稳"，也就是要有最大安全距离

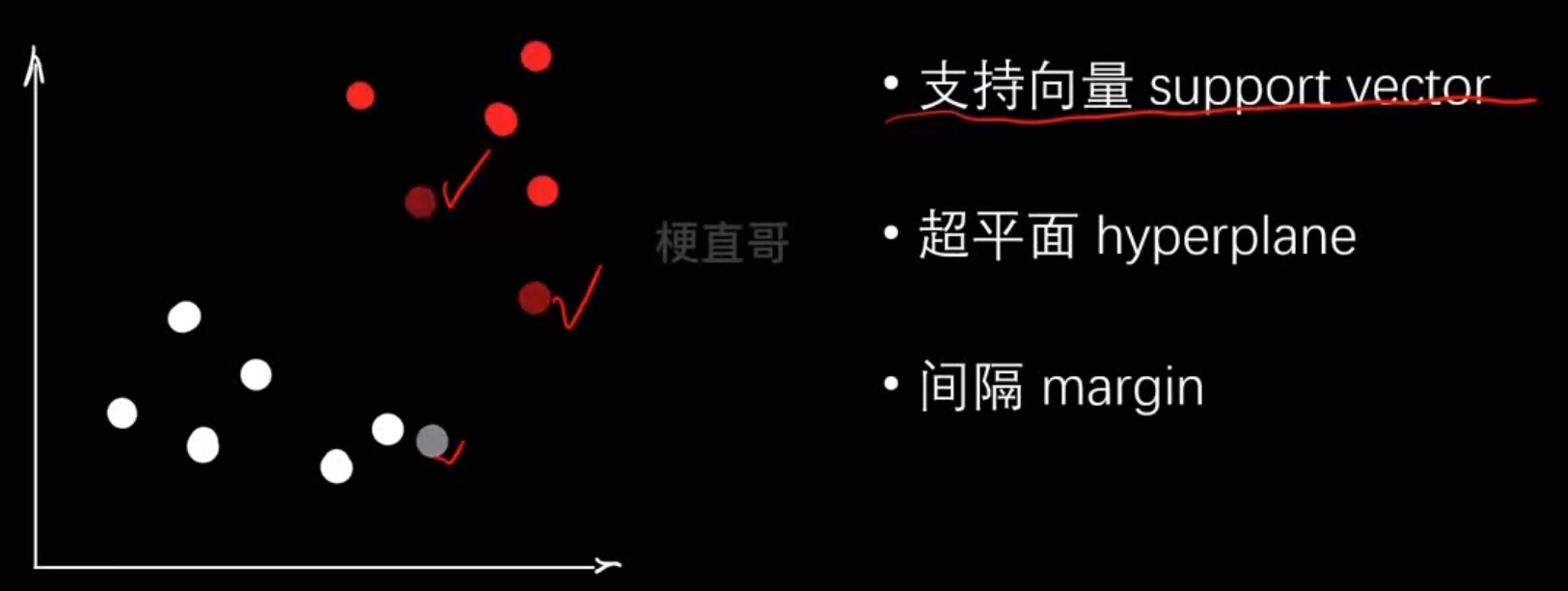
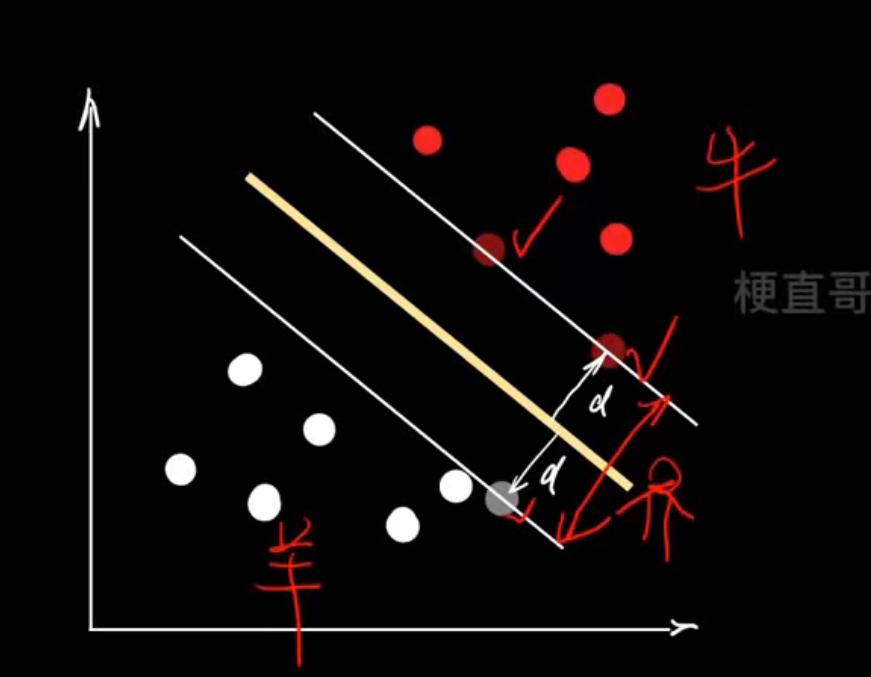
步骤 图中含义 数学含义
1️⃣ 拿到数据 红点 vs 白点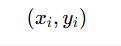
2️⃣ 假设一条线 黄色线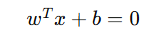
3️⃣ 计算每个点到线的距离 红色箭头 (d)
4️⃣ 最大化两类点的最小距离 白色线之间的距离
5️⃣ 得到支持向量 靠近白线的点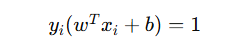

支持向量机就是：在所有能分开两类样本的线中，找那条离两类最近样本最远的线

与线性模型对比：

模型 分类标准 核心思想 优化化目标 泛化能力
线性模型 决策边界 民主投票 点到直线距离和 一般
SVM 超平面 民主集中 margin 提升

硬间隔SVM

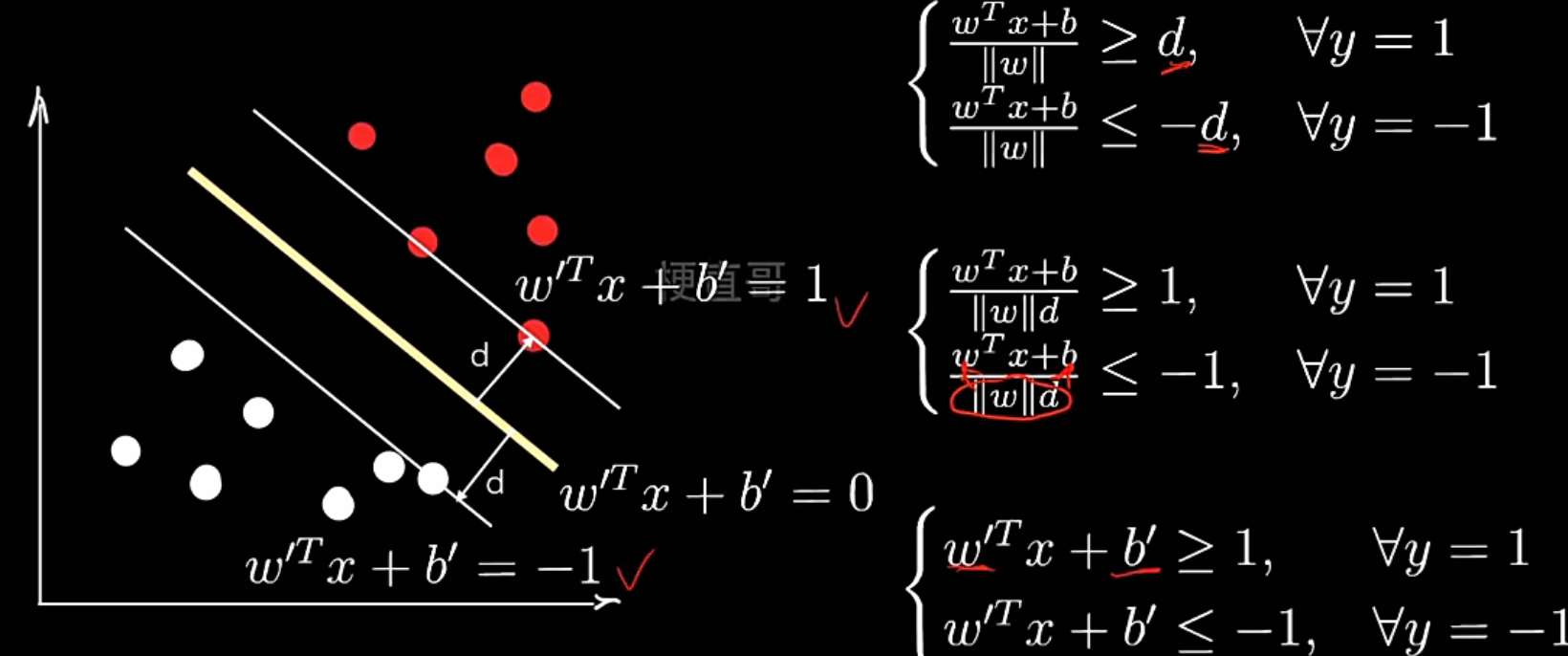
最大间隔超平面：

间隔margin：

"硬"表示 所有样本都必须严格正确分类。换句话说，任何样本点都不能违反约束：

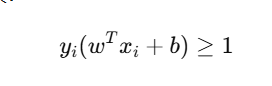
不允许有：

  • 误分类；
  • 落在 margin 区域内的点。

因此，它假设数据是完全线性可分的

说白了硬间隔 SVM本质上就是一个带不等式约束的最优化问题

SVM软间隔

  1. 什么是软间隔？

软间隔 SVM 是在"最大化间隔"和"最小化分类错误"之间找到最佳平衡的凸优化问题。

建立容错机制，进一步提升泛化能力

其核心思想是：允许犯错，但要付出代价

  1. 如何做到？

引入松弛变量：

  1. 目标函数如何权衡"间隔最大化"和"错误最小化"？

C 控制"间隔宽度"和"错误容忍"的平衡：

  • C 大 → 惩罚错误更重 → 模型更严格，倾向于小间隔、低训练误差（可能过拟合）
  • C 小 → 允许更多误差 → 间隔更宽，倾向于高泛化能力（可能欠拟合）

可以这么理解：C 就是"惩罚系数"，相当于老师对犯错的学生到底严不严格

线性SVM分类任务代码实现

python 复制代码 
# 数据集
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

x,y=make_blobs(
    n_samples=40,
    centers=2,
    random_state=0
)

plt.scatter(x[:,0],x[:,1],c=y)
plt.show()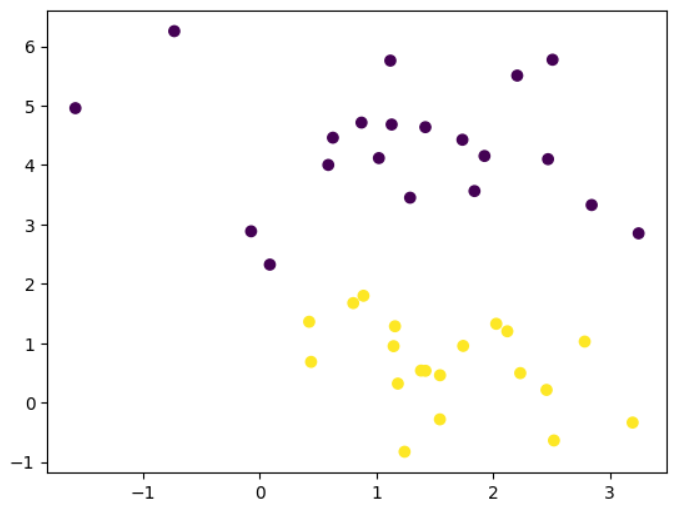
python 复制代码 
# sklearn中的线性SVM
from sklearn.svm import LinearSVC
clf=LinearSVC(C=1)
clf.fit(x,y)
clf.score(x,y)  #1.0
python 复制代码 
# 画决策边界
def decision_boundary_plot(X, y, clf):
    axis_x1_min, axis_x1_max = X[:,0].min() - 1, X[:,0].max() + 1
    axis_x2_min, axis_x2_max = X[:,1].min() - 1, X[:,1].max() + 1
    
    x1, x2 = np.meshgrid( np.arange(axis_x1_min,axis_x1_max, 0.01) , np.arange(axis_x2_min,axis_x2_max, 0.01))
    z = clf.predict(np.c_[x1.ravel(),x2.ravel()])
    z = z.reshape(x1.shape)
    
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#F5B9EF','#BBFFBB','#F9F9CB'])

    plt.contourf(x1, x2, z, cmap=custom_cmap)
    plt.scatter(X[:,0], X[:,1], c=y)
    plt.show()
decision_boundary_plot(x,y,clf)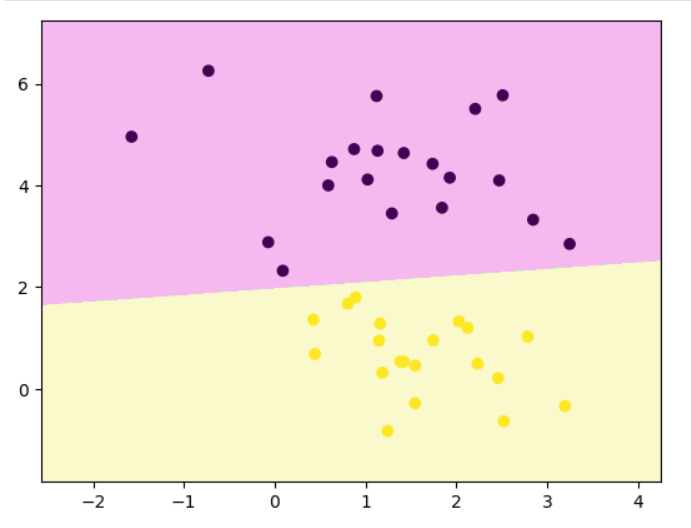
python 复制代码 
# 可视化支持向量机（SVM）的决策边界和间隔线
def plot_svm_margin(x, y, clf, ax = None):
    from sklearn.inspection import DecisionBoundaryDisplay
    DecisionBoundaryDisplay.from_estimator(
        clf,
        x,
        ax = ax,
        grid_resolution=50,
        plot_method="contour",
        colors="k",
        levels=[-1, 0, 1],
        alpha=0.5,
        linestyles=["--", "-", "--"],
    )
    plt.scatter(x[:,0], x[:,1], c = y)
plot_svm_margin(x,y,clf)
plt.show()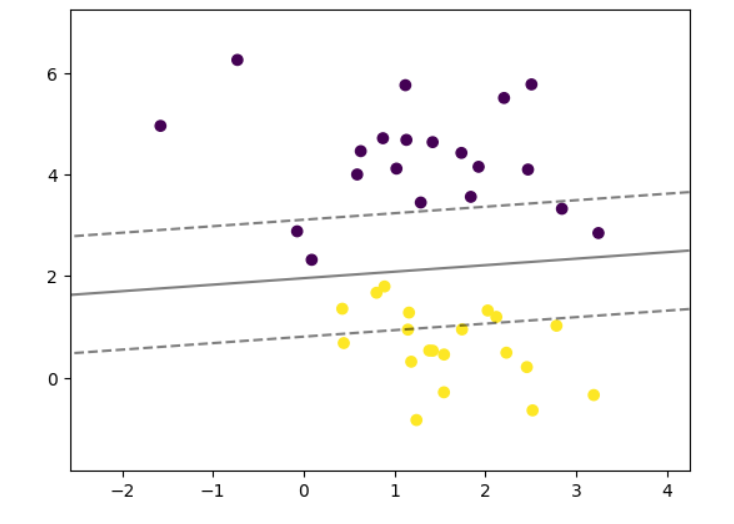
python 复制代码 
# 依次看一下不同的C值对分类的影响
plt.rcParams["figure.figsize"] = (12, 8)

params = [0.1, 1, 10, 100]
for i, c in enumerate(params):
    clf = LinearSVC(C = c, random_state=0)
    clf.fit(x, y)
    
    ax = plt.subplot(2, 2, i + 1)
    plt.title("C: {0}".format(c))
    plot_svm_margin(x, y, clf, ax)
    
plt.show()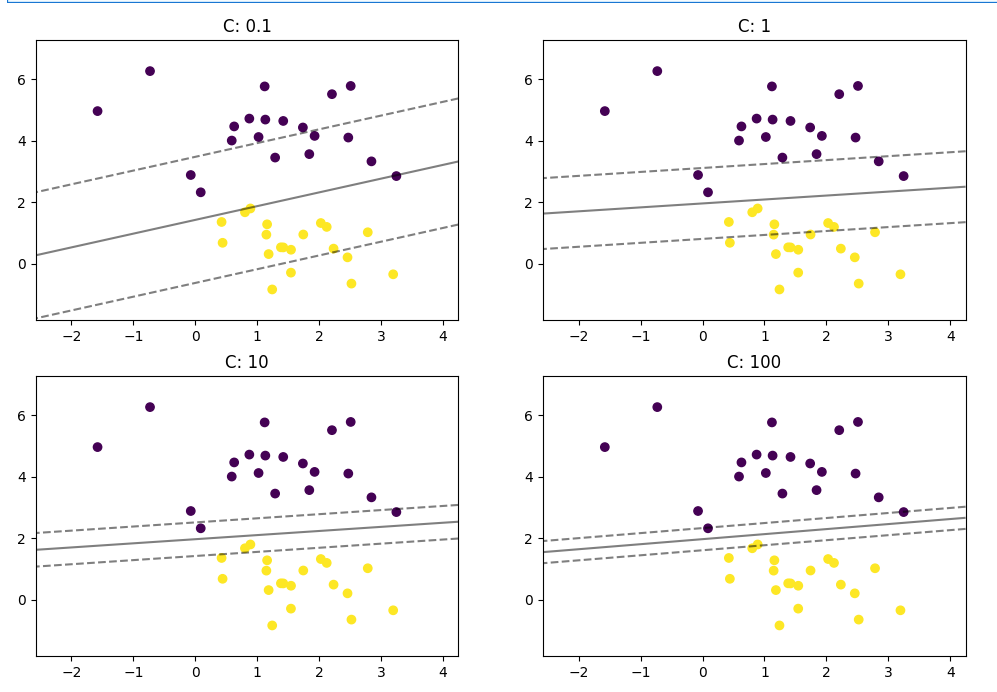

由图分析：

C 值 惩罚强度 间隔宽度 分类精度 泛化表现
小 (0.1) 低（容错高） 宽 错误多 稳定但欠拟合
中 (1) 适中 合理 平衡 泛化最好
大 (10--100) 高（严苛） 窄 训练集高精度 容易过拟合
python 复制代码 
# 支持向量机解决多分类
from sklearn import datasets

iris=datasets.load_iris()
x=iris.data
y=iris.target
clf=LinearSVC(C=0.1,multi_class='ovr',random_state=0)
clf.fit(x,y)

clf.predict(x)
python 复制代码 
# 看看准确率
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y, clf.predict(x))
print("准确率：", accuracy)   #0.96

非线性SVM：核技巧

线性不可分问题：

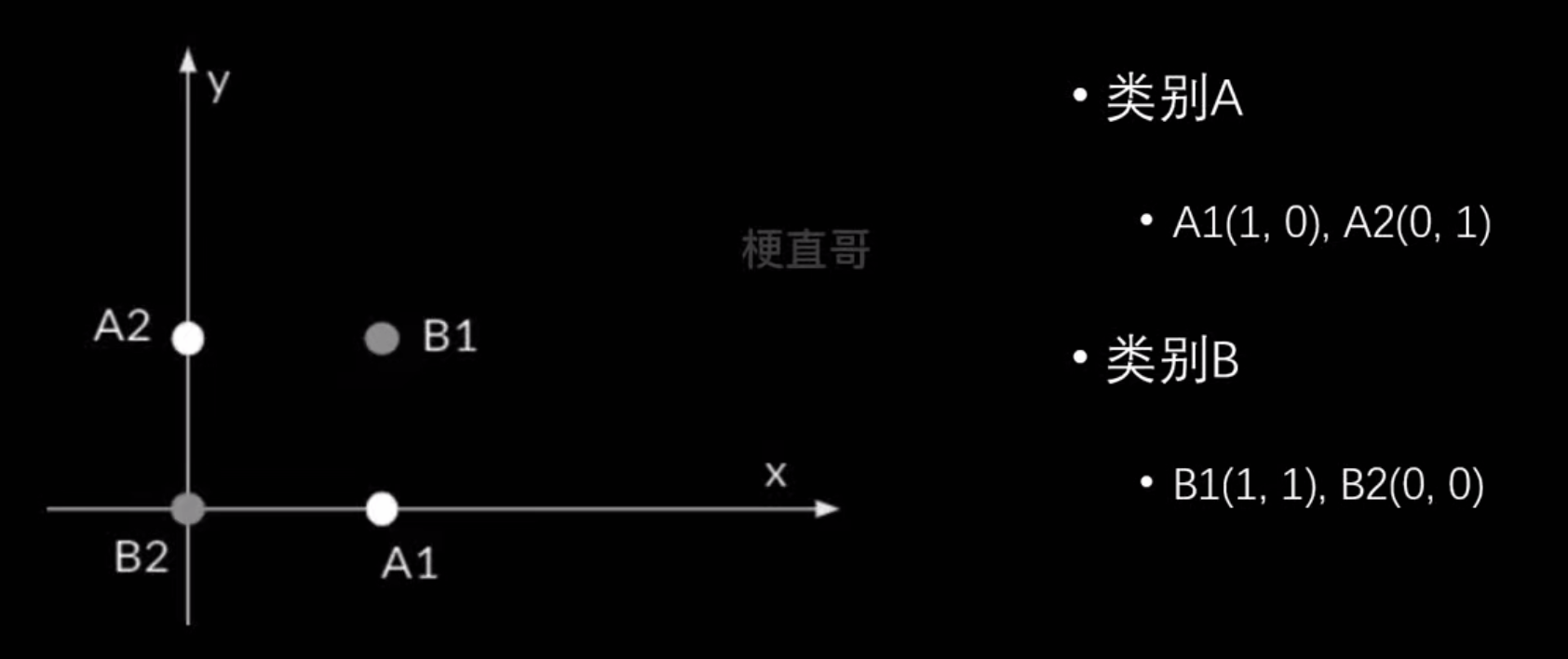
怎么解决？升维映射

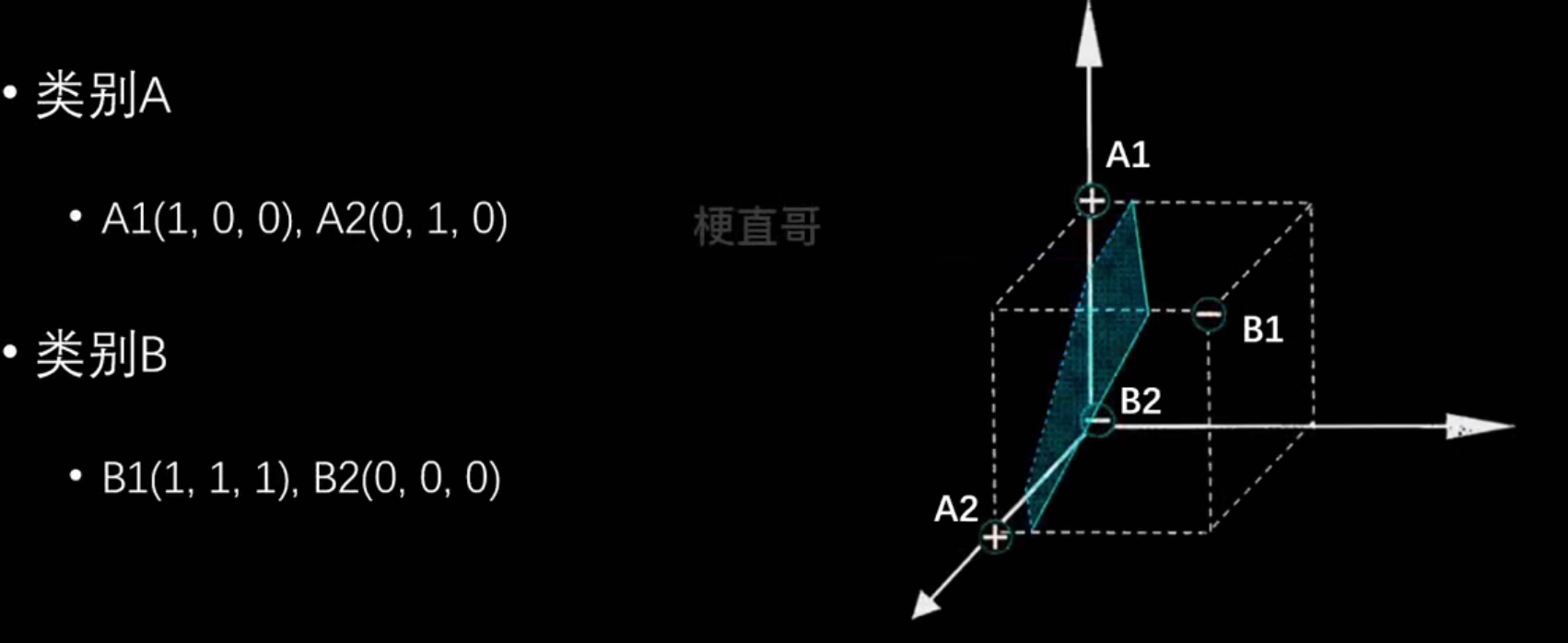
核技巧：

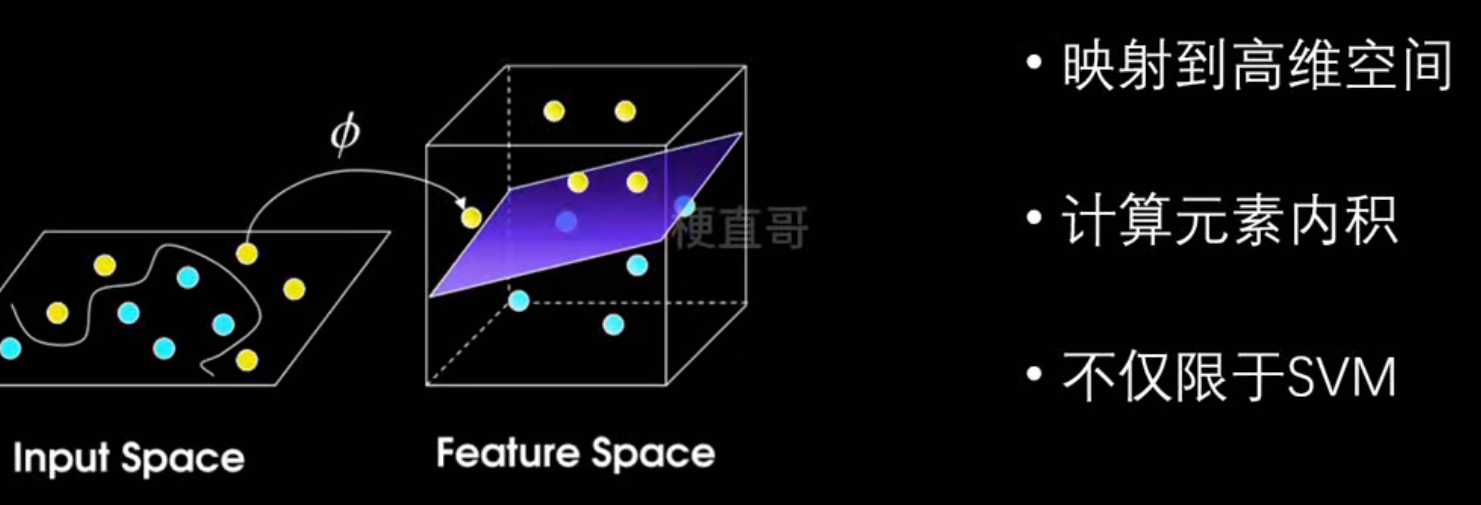
常用核函数：

SVM核函数

此处讲讲多项式核函数：

多项式核解决非线性

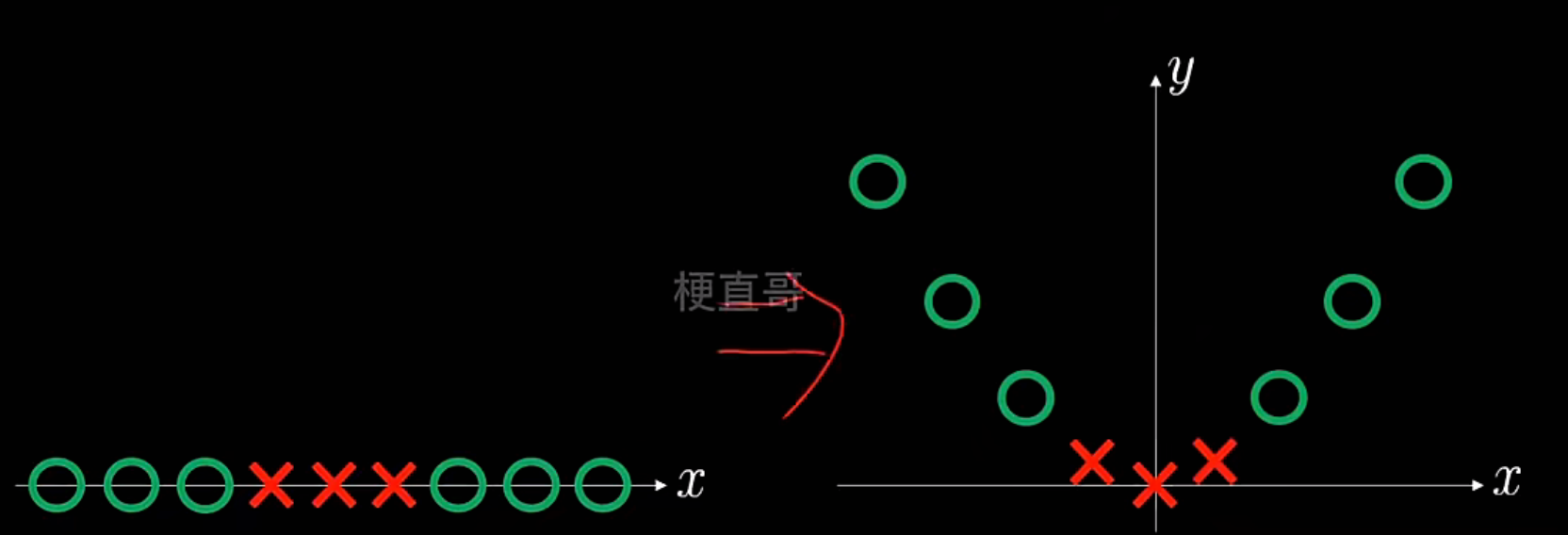
高斯核函数解决非线性问题

非线性SVM分类任务代码实现

对比项 线性 SVM 非线性 SVM
数据分布 样本在原空间中线性可分 样本在原空间中线性不可分
决策边界 一条直线 / 超平面 一条曲线 / 曲面（在原空间）
思想 直接在原空间找最大间隔超平面 先隐式映射到高维空间，再找线性超平面（核函数）
几何效果 平面划分两类 高维超平面在原空间表现为非线性边界
python 复制代码 
# 数据集----这是线性不可分模型
import numpy as np
import matplotlib.pyplot as plt

from sklearn.datasets import make_moons
# make_moons生成非线性数据
x, y = make_moons(n_samples=100, noise=0.2, random_state=0)

plt.scatter(x[:,0], x[:,1], c = y)
plt.show()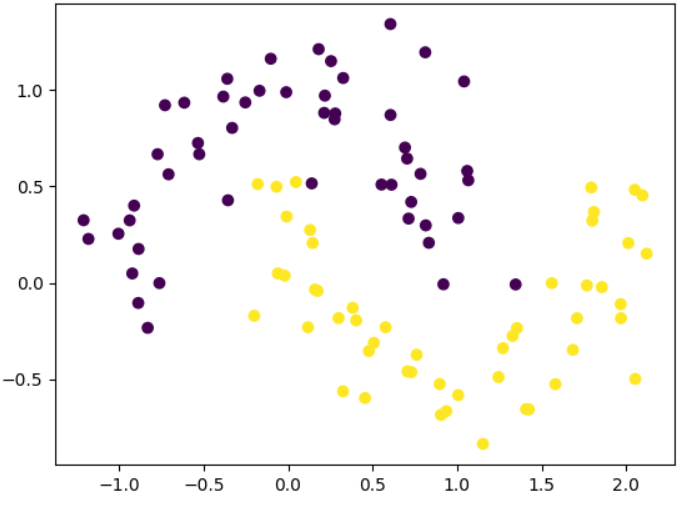
python 复制代码 
# 线性 SVM 决策边界可视化函数
from sklearn.svm import LinearSVC

lsvc = LinearSVC()
lsvc.fit(x,y)

def decision_boundary_plot(X, y, clf):
    axis_x1_min, axis_x1_max = X[:,0].min() - 1, X[:,0].max() + 1
    axis_x2_min, axis_x2_max = X[:,1].min() - 1, X[:,1].max() + 1
    
    x1, x2 = np.meshgrid( np.arange(axis_x1_min,axis_x1_max, 0.01) , np.arange(axis_x2_min,axis_x2_max, 0.01))
    z = clf.predict(np.c_[x1.ravel(),x2.ravel()])
    z = z.reshape(x1.shape)
    
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#F5B9EF','#BBFFBB','#F9F9CB'])

    plt.contourf(x1, x2, z, cmap=custom_cmap)
    plt.scatter(X[:,0], X[:,1], c=y)
    plt.show()

decision_boundary_plot(x,y,lsvc)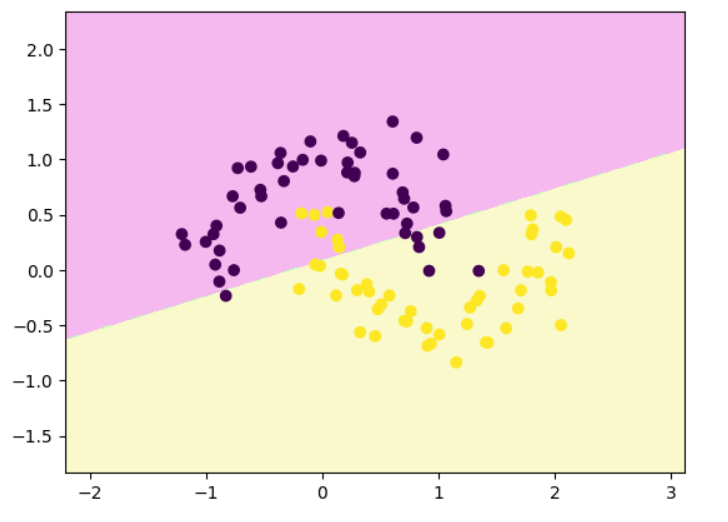

显式多项式升维 + 线性 SVM

python 复制代码 
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.pipeline import Pipeline
poly_svc = Pipeline([
    ("poly", PolynomialFeatures(degree=3)),  #拐两个弯
    ("std_scaler", StandardScaler()),
    ("linearSVC", LinearSVC())
])

poly_svc.fit(x,y)

decision_boundary_plot(x,y,poly_svc)

代码里的 LinearSVC 确实是 线性核 SVM ，但由于前面加了 PolynomialFeatures(degree=3)，整体模型相当于在高维多项式空间中训练线性 SVM，在原始特征空间表现为一个 非线性（弯曲）决策边界。

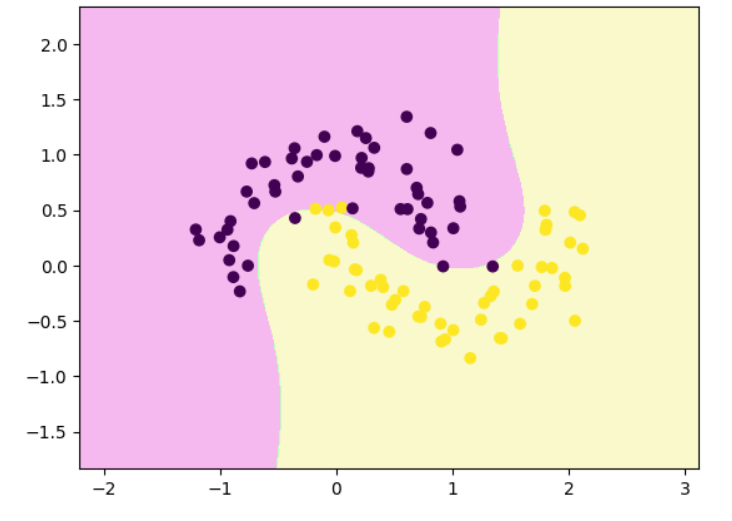
多项式核函数解决非线性问题

参数 作用 默认值 说明
degree 多项式的次数 (d) 3 决定映射的"弯曲复杂度"
coef0 常数项 ® 0 决定低阶项与高阶项的权重
gamma 核宽度系数 'scale' 控制特征缩放（和 RBF 类似）
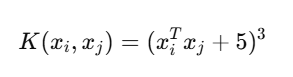
python 复制代码 
# 多项式核 SVM
from sklearn.svm import SVC
poly_svc = Pipeline([
    ("std_scaler", StandardScaler()),
    ("polySVC", SVC(kernel='poly', degree=3, coef0=5 ))
])
poly_svc.fit(x,y)
decision_boundary_plot(x,y,poly_svc)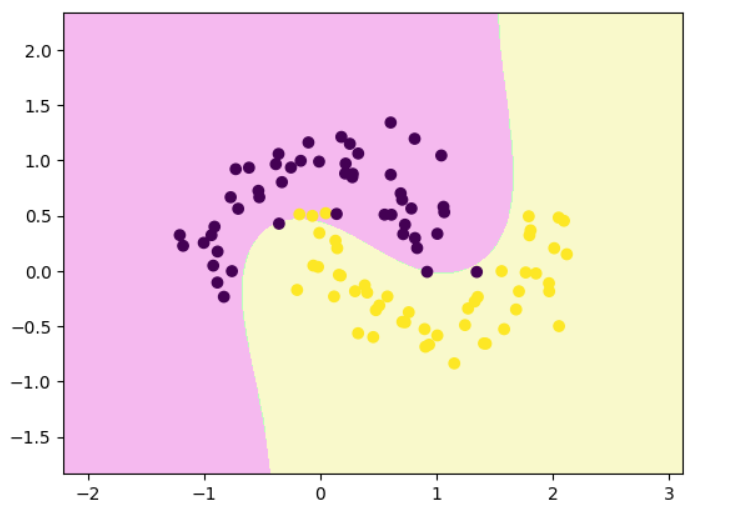

高斯核函数

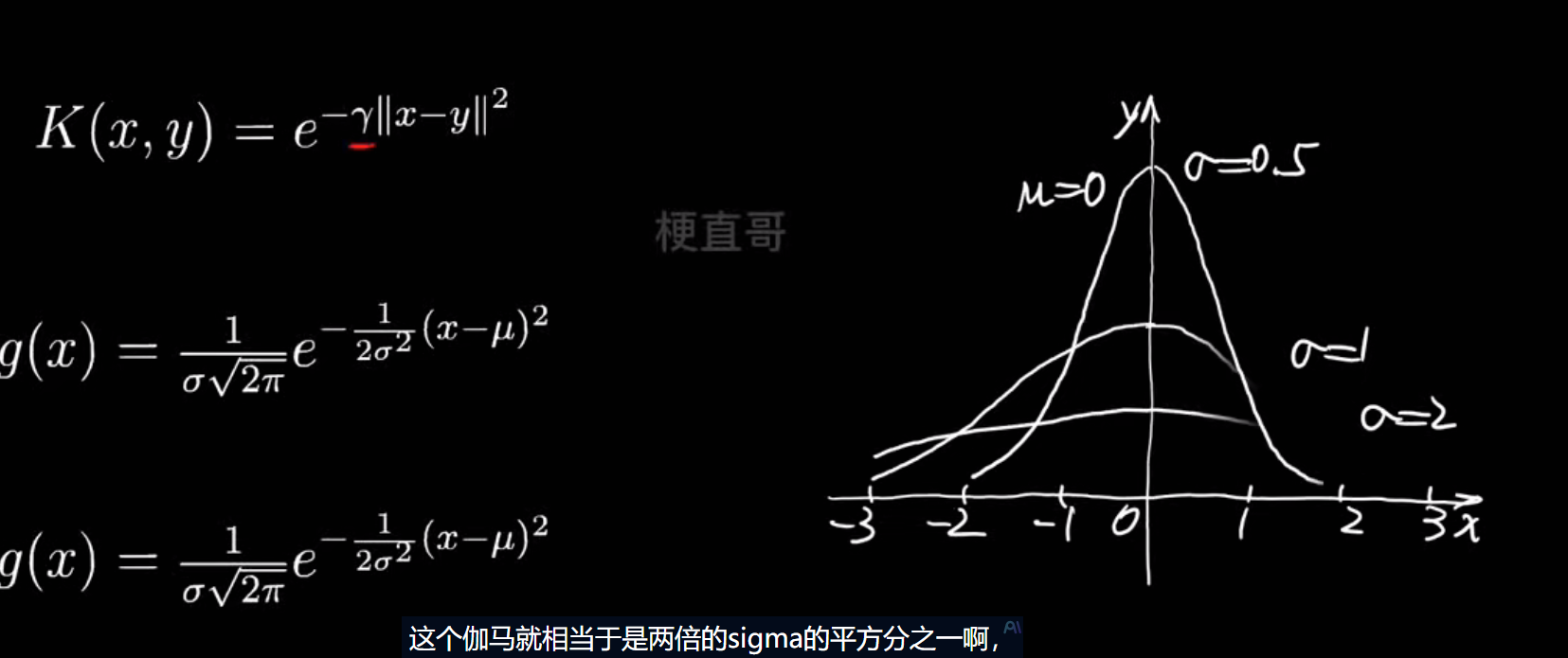
sigma越大，曲线越平缓

python 复制代码 
rbf_svc = Pipeline([
    ("std_scaler", StandardScaler()),
    ("rbfSVC", SVC(kernel='rbf', gamma=0.1 ))
])


rbf_svc.fit(x,y)
decision_boundary_plot(x,y,rbf_svc)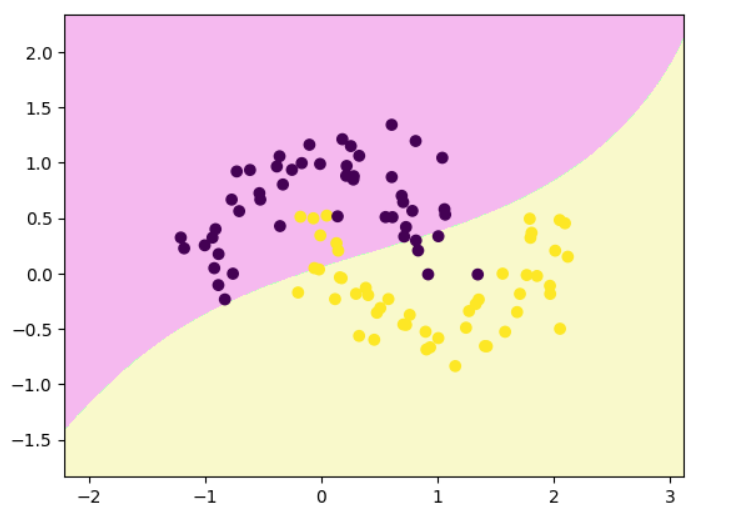
python 复制代码 
rbf_svc = Pipeline([
    ("std_scaler", StandardScaler()),
    ("rbfSVC", SVC(kernel='rbf', gamma=10 ))
])
rbf_svc.fit(x,y)
decision_boundary_plot(x,y,rbf_svc)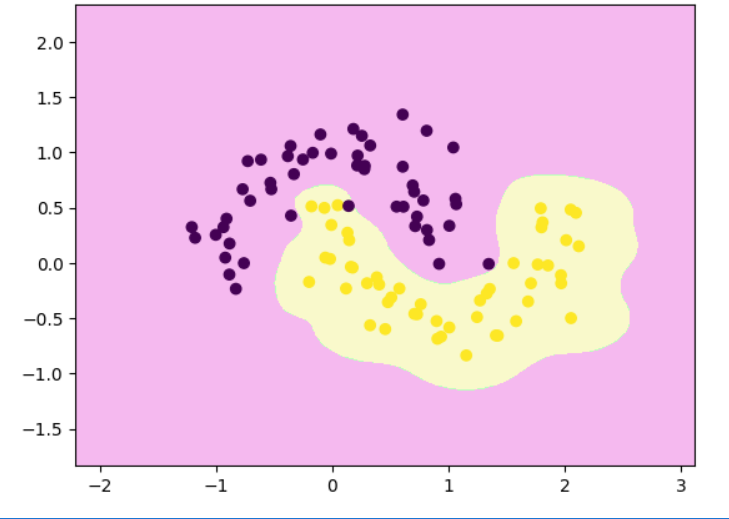
python 复制代码 
rbf_svc = Pipeline([
    ("std_scaler", StandardScaler()),
    ("rbfSVC", SVC(kernel='rbf', gamma=100 ))
])
rbf_svc.fit(x,y)
decision_boundary_plot(x,y,rbf_svc)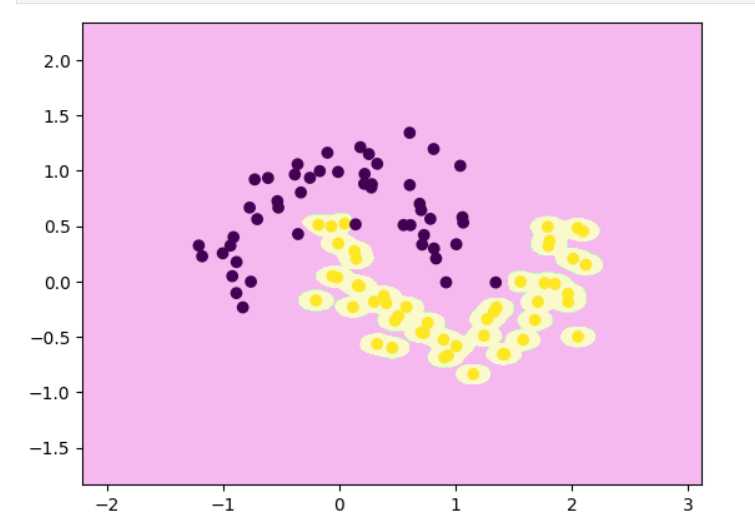
γ 的取值（gamma） 样本的"影响半径" 决策边界 模型复杂度 泛化能力
小（如 0.1） 每个样本影响范围大 边界平滑 简单 泛化强（但可能欠拟合）
中（如 10） 影响范围适中 边界适度弯曲 较复杂 泛化良好
大（如 100） 每个样本只影响极近邻 边界剧烈弯曲 极复杂 容易过拟合

如何选择核函数？

  • 当特征多且接近样本数量，可直接选择线性核SVM
  • 当特征数少，样本数正常，推荐选择高斯核函数
  • 当特征数少，样本数很大，建议选择多项式核函数

SVM回归任务代码实现

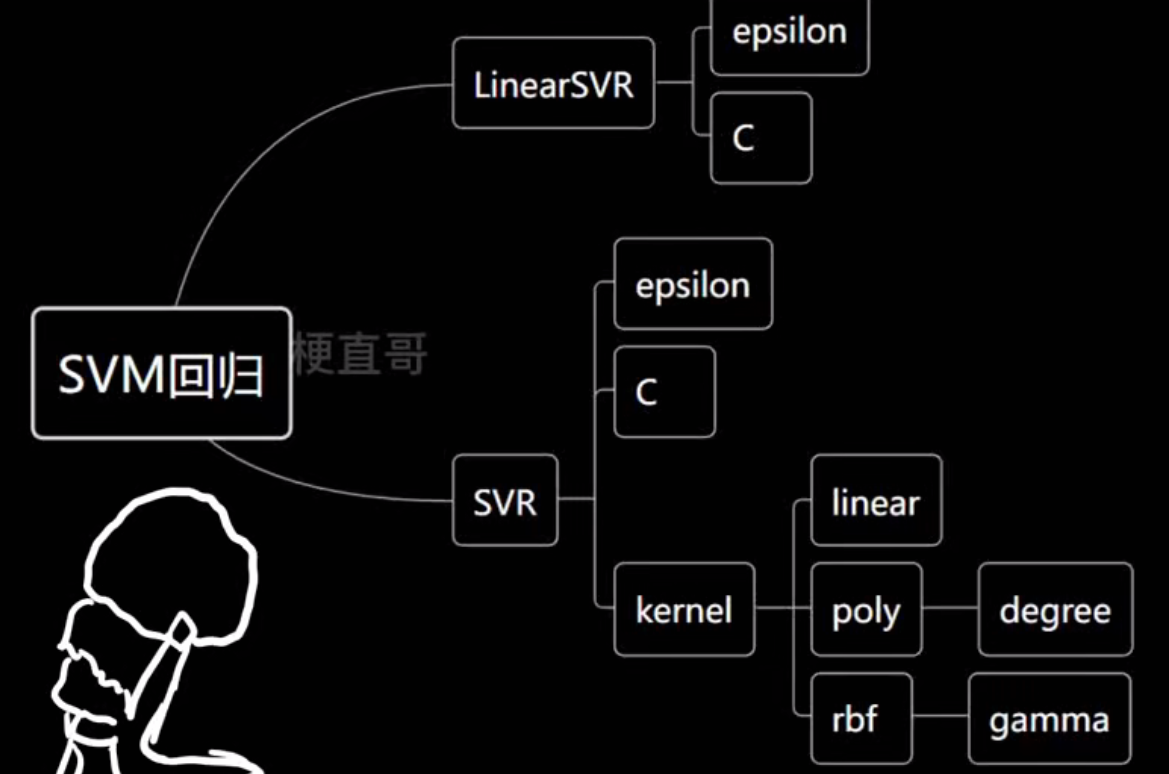
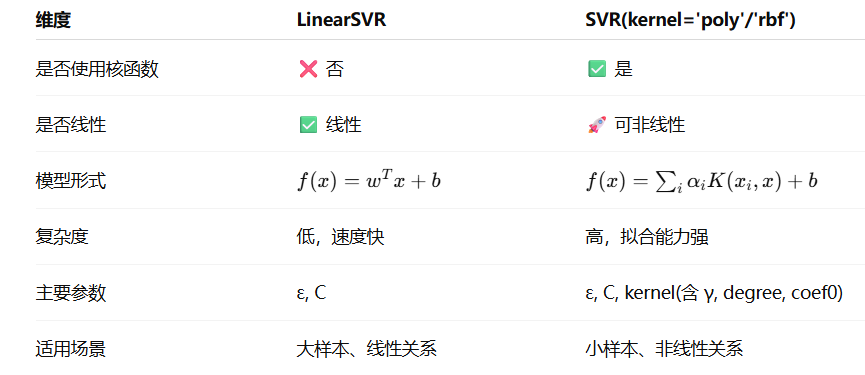
SVM回归分两类：

类型 说明
LinearSVR 线性支持向量回归（不使用核函数）
SVR 核支持向量回归（可使用多种核函数，如 RBF、多项式等）
python 复制代码 
# 数据集
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(666)
x = np.random.uniform(-3,3,size=100)
y = 0.5 * x**2 +x +2 +np.random.normal(0,1,size=100)
X = x.reshape(-1,1)

plt.scatter(x,y)
plt.show()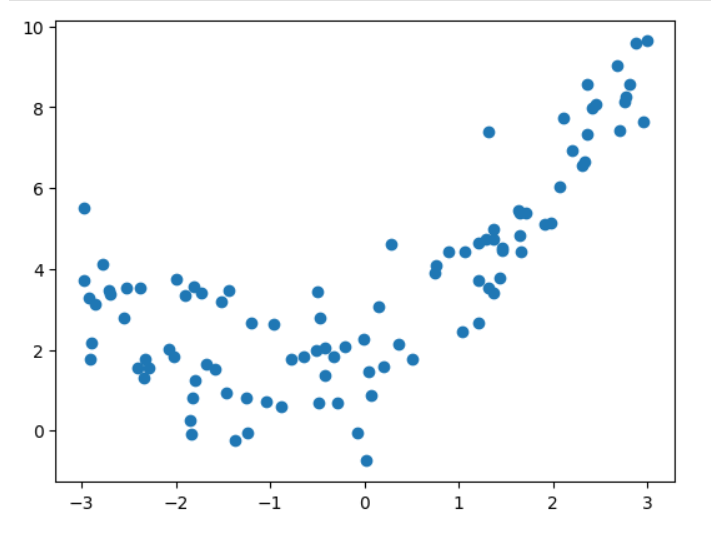
python 复制代码 
# 线性SVR
# 线性支持向量回归
from sklearn.svm import LinearSVR
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline

def StandardLinearSVR(epsilon=0.1):
    return Pipeline([
        ("std_scaler",StandardScaler()),
        ("linearSVR",LinearSVR(epsilon=epsilon))
    ])

svr = StandardLinearSVR()
svr.fit(X,y)
y_predict = svr.predict(X)
plt.scatter(x,y)
plt.plot(np.sort(x),y_predict[np.argsort(x)],color='r')
plt.show()

svr.score(X,y)  #0.48764762540009954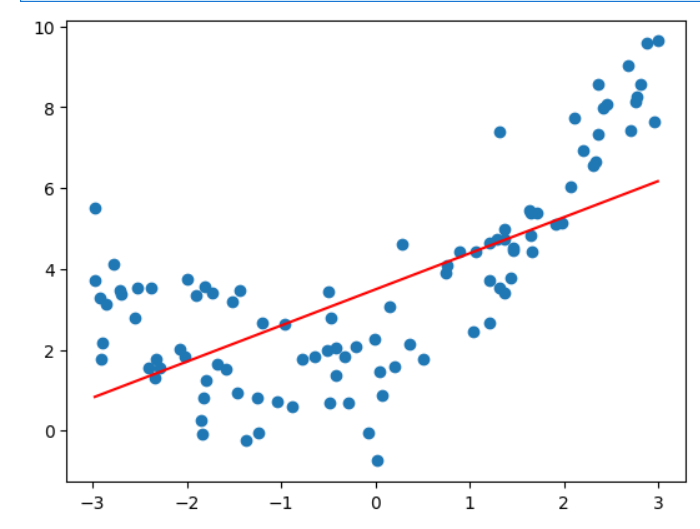
python 复制代码 
# RBF核SVR
# 带 RBF 核的支持向量回归
from sklearn.svm import SVR
def StandardSVR(epsilon=0.1):
    return Pipeline([
        ('std_scaler',StandardScaler())
        ,('SVR',SVR(kernel='rbf',epsilon=epsilon))   #高斯核函数
    ])
svr = StandardSVR()
svr.fit(X,y)
y_predict = svr.predict(X)
plt.scatter(x,y)
plt.plot(np.sort(x),y_predict[np.argsort(x)],color='r')
plt.show()

svr.score(X,y)  # 0.8138647789256848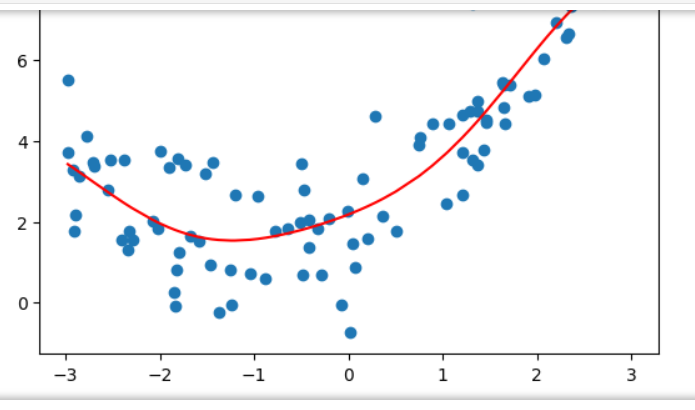

SVM优缺点和适用条件

优点：

  • 高效处理非线性数据
  • 良好的泛化能力
  • 解决分类和回归问题
  • 稳定性

缺点：

  • 选择合适的核函数比较困难
  • 大量内存需求
  • 大数据集上训练时间长
  • 难以解释

7、集成学习

团结就是力量

日常生活中普遍存在的决策思想

兼听则明，偏信则暗

集成学习核心思想和原理

与其依赖一个复杂的模型，不如集合多个相对简单（或不同）的模型，通过某种方式将它们的结果组合起来，从而获得一个更强大、更稳定、更精确的最终模型

既可以监督学习，也可以无监督学习

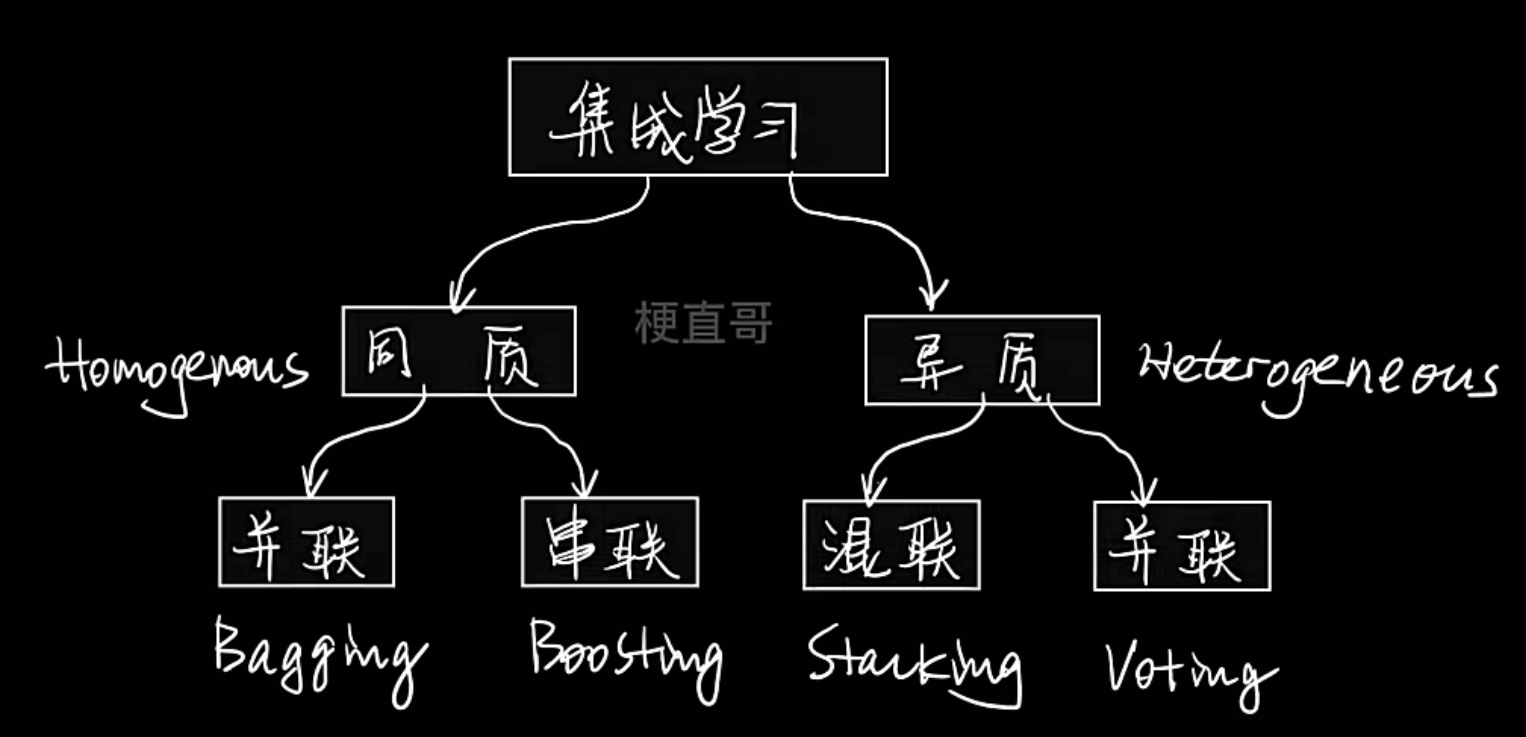
  • 同质
    • 含义 ：所有基学习器都是同一种类型的模型，比如全是决策树，或者全是神经网络
    • 举例：随机森林（全是决策树）、AdaBoost（通常使用决策树桩）
  • 异质
    • 含义 ：基学习器是不同类型的模型，比如一个支持向量机 + 一个决策树 + 一个逻辑回归模型。
    • 举例：Voting 和 Stacking 方法常使用异质学习器
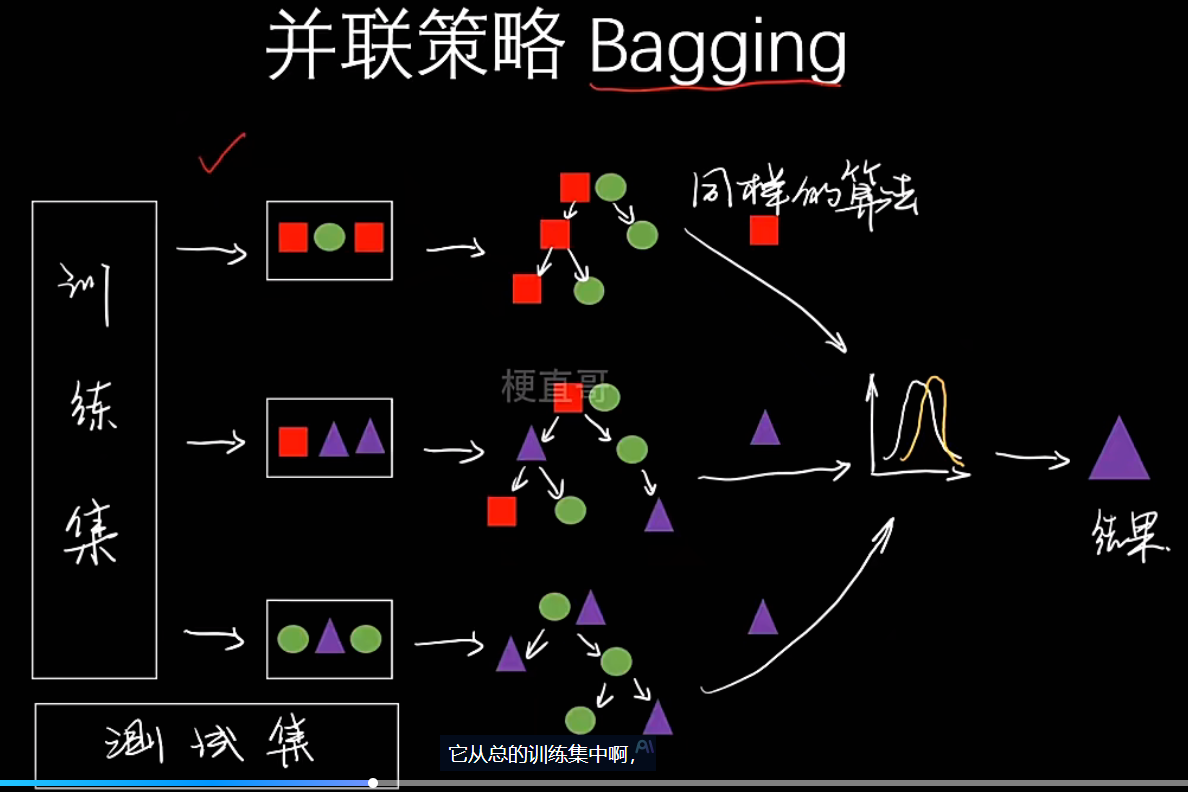
  • 并联
    • 含义 ：所有基学习器可以独立、并行地进行训练。它们之间没有依赖关系。
    • 代表算法 ：Bagging 和 Voting(少数服从多数)
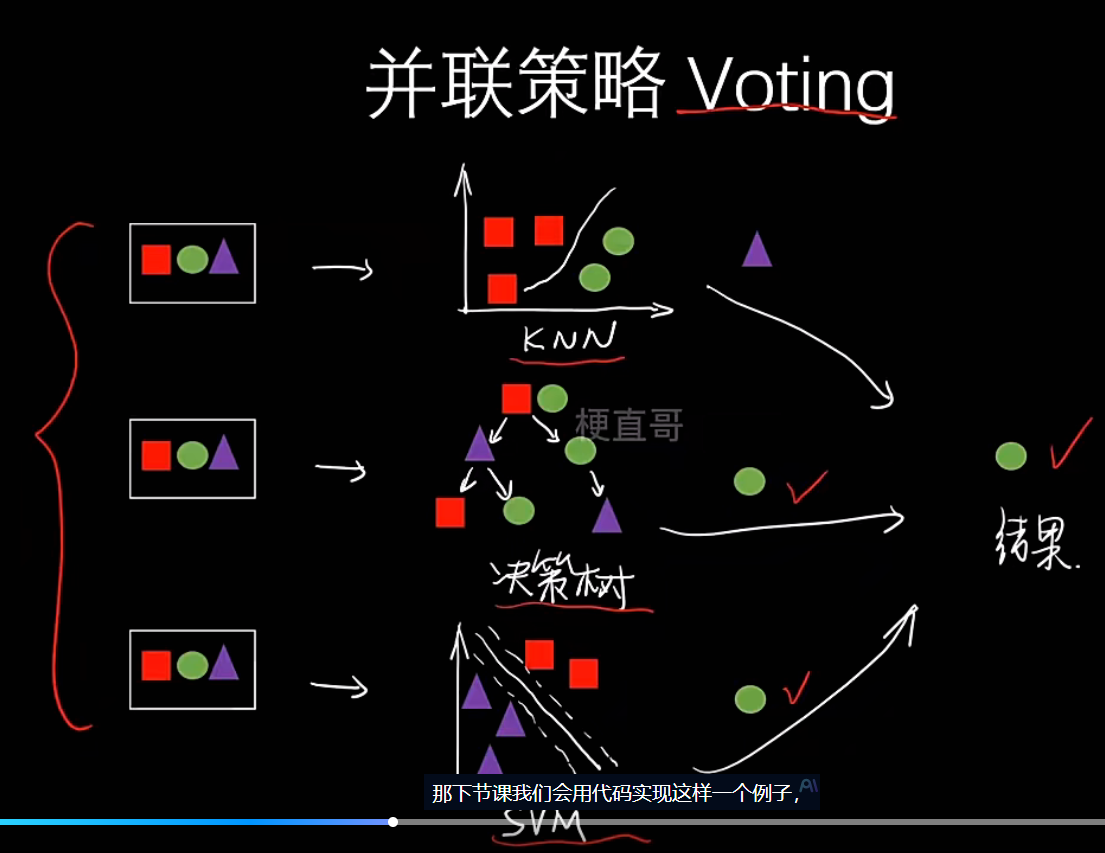
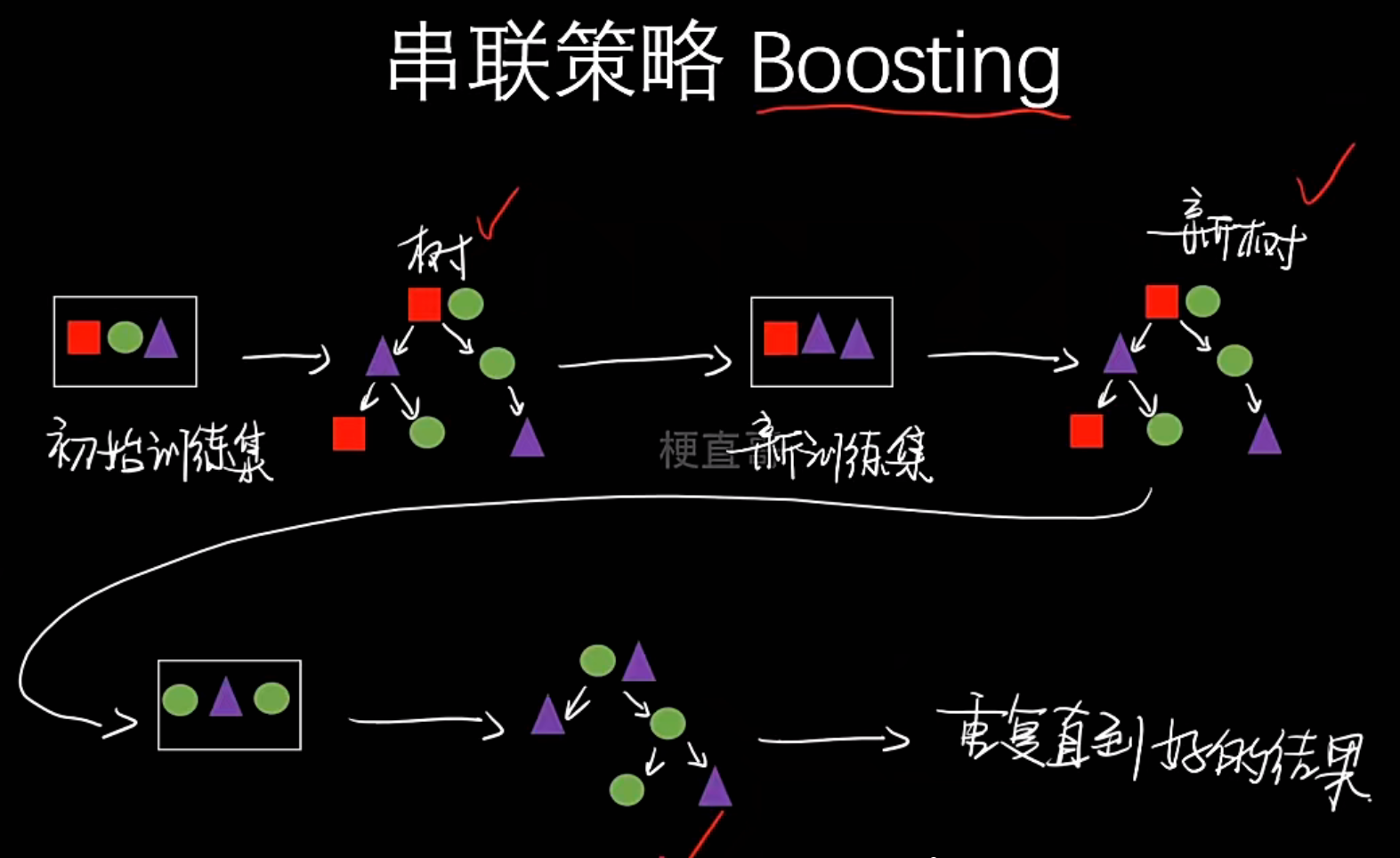
  • 串联
    • 含义 ：基学习器需要按顺序依次训练。后一个学习器的训练依赖于前一个学习器的结果（比如，重点关注前一个学习器分错的样本）
    • 代表算法 ：Boosting
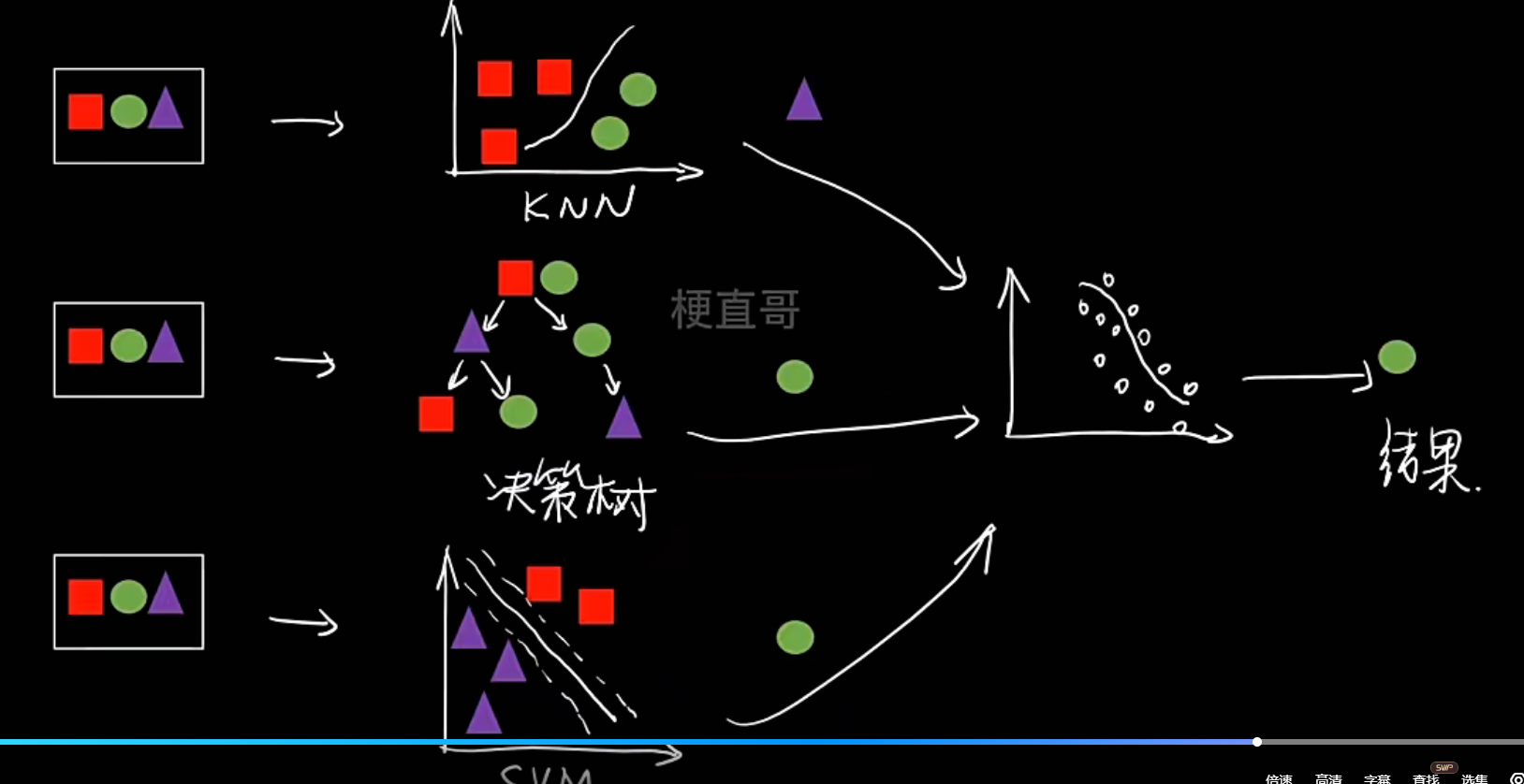
  • 混联
    • 含义：结合了并联和串联的特点，是一种更复杂的层次化结构
    • 代表算法 ：Stacking 。它第一层是多个并联 的基学习器（可以是同质或异质），第二层再串联一个元学习器来整合第一层的结果
  • Bagging
    • 类型 ：同质
    • 组合方式 ：并联
    • 核心思想 ：通过自助采样训练多个模型，然后"投票"或"平均"结果。旨在降低方差，防止过拟合
    • 典型代表 ：随机森林
  • Boosting
    • 类型 ：同质
    • 组合方式 ：串联
    • 核心思想 ：顺序训练模型，后续模型专注于修正前序模型的错误。旨在降低偏差，提升模型精度
    • 典型代表 ：AdaBoost, GBDT, XGBoost, LightGBM
  • Stacking
    • 类型 ：通常为异质（也可以是同质）
    • 组合方式 ：混联（先并联，后串联）
    • 核心思想 ：训练多个不同的基模型，然后将它们的预测结果作为新的特征，再训练一个"元模型"来进行最终决策。旨在博采众长。

集成学习代码实现

python 复制代码 
# 数据集
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons

x,y=make_moons(
    n_samples=1000,
    noise=0.4,
    random_state=20
)
x.shape,y.shape

输出：
((1000, 2), (1000,))

plt.scatter(x[:,0],x[:,1],c=y,s=10)
plt.show()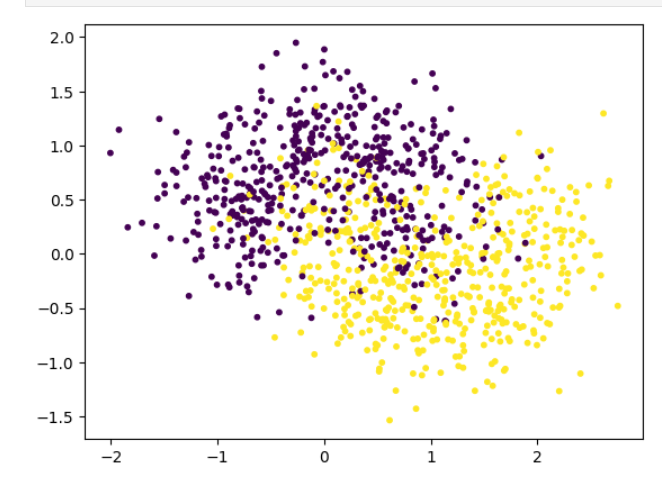
python 复制代码 
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=0)
python 复制代码 
# 手动实现集成学习的分类器
# 创建三个不同的分类器

from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB

clf=[
    KNeighborsClassifier(n_neighbors=3),
    LogisticRegression(),
    GaussianNB()
]
# 打印分类器在测试集上的score
for i in range(len(clf)):
    clf[i].fit(x_train,y_train)
    print(clf[i].score(x_test,y_test))

输出：
0.832
0.848
0.848
python 复制代码 
# 三个分类器分别预测到的投票的结果
y_pred=np.zeros_like(y_test)
# 三个分类器分别对测试集进行预测
# 每个分类器的预测结果（0或1）被累加到 y_pred 中
# 最终 y_pred 中每个位置的值表示"有多少个分类器预测该样本为类别1"
for i in range(len(clf)):
    y_pred+=clf[i].predict(x_test)
y_pred[y_pred<2]=0
y_pred[y_pred>=2]=1
y_pred
python 复制代码 
from sklearn.metrics import accuracy_score
accuracy_score(y_test,y_pred)

输出：
0.852
python 复制代码 
# 使用sklearn中的集成学习方法
from sklearn.ensemble import VotingClassifier
clf=[
    KNeighborsClassifier(n_neighbors=3),
    LogisticRegression(),
    GaussianNB()
]

vclf=VotingClassifier(
    estimators=[
        ('knn',clf[0]),
        ('lr',clf[1]),
        ('gnb',clf[2])
    ],
    # 每个基分类器独立预测，最终结果采用"少数服从多数"原则
    voting='hard',
    # 并行处理参数
    n_jobs=-1
)
vclf.fit(x_train,y_train)
vclf.score(x_test,y_test)

输出:
0.852

但这种投票策略存在问题：

于是我们采用另一种情况：概率求和或者看平均值作为置信度

soft表示软投票，即

python 复制代码 
# 每个分类器给出属于每个类别的概率
KNN: [P(0)=0.3, P(1)=0.7]    # 预测为1的概率是0.7
LR:  [P(0)=0.6, P(1)=0.4]    # 预测为1的概率是0.4  
NB:  [P(0)=0.2, P(1)=0.8]    # 预测为1的概率是0.8

# 平均概率
平均P(0) = (0.3 + 0.6 + 0.2) / 3 = 0.37
平均P(1) = (0.7 + 0.4 + 0.8) / 3 = 0.63

# 最终选择概率更高的类别
最终结果: 1 (因为0.63 > 0.37)
python 复制代码 
# 获取概率：每个分类器输出属于各个类别的概率
# 平均概率：计算所有分类器概率的平均值
# 选择类别：选择平均概率最高的类别作为最终预测
vclf=VotingClassifier(
    estimators=[
        ('knn',clf[0]),
        ('lr',clf[1]),
        ('gnb',clf[2])
    ],
    voting='soft',
    # 并行处理参数
    n_jobs=-1
)
vclf.fit(x_train,y_train)
vclf.score(x_test,y_test)

输出：
0.868
相关推荐
萌萌可爱郭德纲3 小时前
基于AI智能算法的装备结构可靠性分析与优化设计技术专题
人工智能·机器学习·支持向量机·发动机·疲劳寿命
诺....3 小时前
机器学习库的决策树绘制
人工智能·决策树·机器学习
nju_spy3 小时前
NJU-SME 人工智能（三） -- 正则化 + 分类 + SVM
人工智能·机器学习·支持向量机·逻辑回归·对偶问题·正则化·auc-roc
不语n4 小时前
快速排序（Quick Sort）详解与图解
数据结构·算法·排序算法·快速排序·双指针排序
电鱼智能的电小鱼4 小时前
基于电鱼 ARM 工控机的AI视频智能分析方案：让传统监控变得更聪明
网络·arm开发·人工智能·嵌入式硬件·算法·音视频
初学者，亦行者5 小时前
Rust性能优化：内存对齐与缓存友好实战
算法·rust
py有趣5 小时前
LeetCode算法学习之杨辉三角
学习·算法·leetcode
小白菜又菜5 小时前
Leetcode 3100. Water Bottles II
算法·leetcode·职场和发展
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03BongoCat - 跨平台键盘猫动画工具04GitLab 零基础入门指南：从安装到项目管理全流程05Linux下V2Ray安装配置指南06NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南07Labelme从安装到标注：零基础完整指南08安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）09在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）10jdk21下载、安装（Windows、Linux、macOS）