一 为什么要使用泰勒公式
先看一段代码
for (k = 0; k < 10; k++)
{
a += b_a[k] * (2.0 / (exp(-2.0 * ((c_a[k] * b_y1 + c_a[k + 10] * c_idx_1) + dv[k])) + 1.0) - 1.0);
}
由于这段函数包含指数运算,指数运算对于一般的单片机而言比较复杂,转换成泰勒多项式计算会大大简化计算的复杂度,减轻CPU的负担,缩短计算时间,尽管会在计算精度上有所损失
二 泰勒公式
1. 泰勒公式核心思想:用"多项式"逼近"复杂函数"
想象你是一个科学家,面对一个复杂的曲线函数,比如 f(x)=exf(x)=ex 或 cos(x)cos(x)。你想在某个点(例如 x=0x=0)附近,用一个简单易懂的多项式来近似它。
为什么?
因为多项式只涉及加、减、乘 和乘方运算,计算非常简单,无论是人还是计算机都能轻松处理。
泰勒展开的核心目标就是:找到一个在特定点附近与复杂函数"最像"的多项式。
2 构建泰勒多项式
假设我们要在点 x=a附近逼近函数 f(x)。我们希望找到一个多项式 P(x):
P(x)=c0+c1(x−a)+c2(x−a)2+c3(x−a)3+...
关键问题是:系数 c0,c1,c2,...应该取什么值,才能让 P(x) 在 x=a 附近最像 f(x)?
答案是:让 P(x) 在 x=a处的函数值,以及尽可能多阶的导数值,都与 f(x)相等。
这里为什么都选用的x-a,而不是x,因为我们要求的是函数值跟导数。用x-a便于计算。
第0步:匹配函数值(位置)
在 x=a处,我们要求多项式等于函数值:
P(a)=f(a)
代入多项式:
c0+c1(0)+c2(0)2+⋯=f(a) ⟹ c0=f(a)
✅ 我们得到了第1个系数: c0=f(a)
多项式等于函数值这个是条件,所以得出c0=F(a);
第1步:匹配一阶导数值(斜率)
我们希望多项式在 x=a 处的切线斜率也和原函数一样:
P′(a)=f′(a)
先求 P(x)的导数:
P′(x)=c1+2c2(x−a)+3c3(x−a)2+...(第二个2.3是平方的意思)见下图,
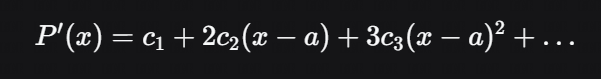
代入 x=a:
P′(a)=c1+0+0+⋯=f′(a) ⟹ c1=f′(a)
✅ 我们得到了第2个系数: c1=f′(a)
x=a 处的切线斜率也和原函数一样,这个是条件,所以得出c1=f′(a),具体求导数的方法要搜索幂函数求导法则,见下图,就是把指数拿下来当系数,然后指数减1。

第3步:匹配三阶导数
继续这个过程:
P′′′(a)=f′′′(a)
P′′′(x)=6c3+24c4(x−a)+...
代入 x=a:
P′′′(a)=6c3=f′′′(a) ⟹ c3=f′′′(a)/6=f′′′(a)/3!
✅ 我们得到了第4个系数: c3=f′′′(a)/3!
3. 泰勒公式的最终形式
继续这个模式,我们就得到了著名的泰勒公式:
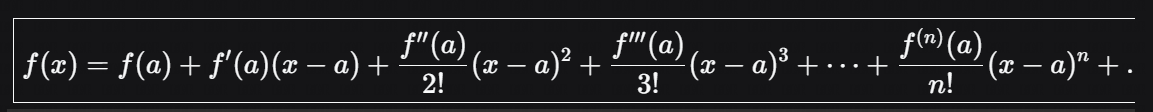
特殊情形:当 a=0a=0 时 ,称为麦克劳林级数:
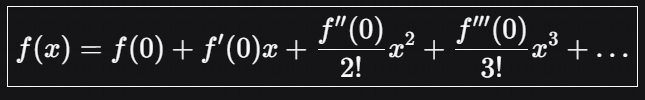
三 Tanh 函数
先看一段代码
for (k = 0; k < 10; k++)
{
a += b_a[k] * (2.0 / (exp(-2.0 * ((c_a[k] * b_y1 + c_a[k + 10] * c_idx_1) + dv[k])) + 1.0) - 1.0);
}
由于这段函数包含指数运算,指数运算对于一般的单片机而言比较复杂,转换成泰勒多项式计算会大大简化计算的复杂度,减轻CPU的负担,缩短计算时间,尽管会在计算精度上有所损失
1. 数学形式
代码中的核心表达式是:
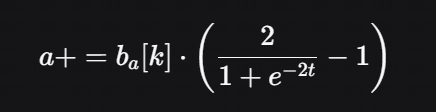
其中
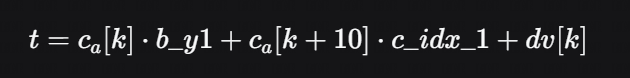
即 t=w1x1+w2x2+b 的形式(这里 dv[k]是偏置项)。

2. 泰勒展开
我们要在 t=0 处展开 tanh(t)。
注意不是所有函数都能用泰勒展开,tanh(t)是双曲正切函数,能够使用泰勒展开式。
已知:
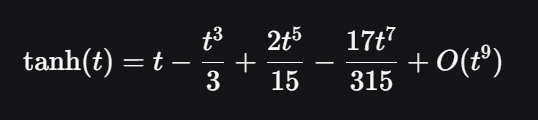
代入 t 的表达式
令:
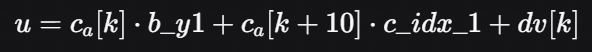
那么:
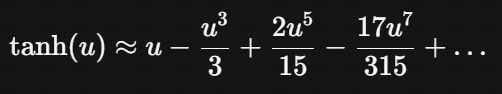
展开到一阶(线性近似)
tanh(u)≈u
所以:
a≈k=0∑9ba[k]⋅u 见上文原代码等价式
展开到三阶
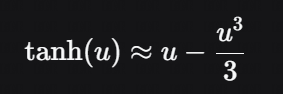
其中
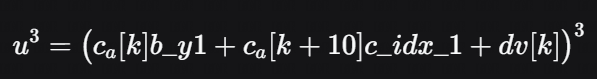
最终计算得到
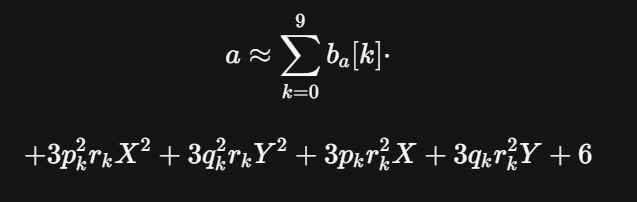
上式有误,知道意思即可
3. 代码表示:
换算成代码的形式可以使用deepseek,复制整段泰勒展开之前的代码进去,输入命令"将次段代码用5阶泰勒展开式替代"
1. 一阶泰勒展开(线性近似)
for (k = 0; k < 10; k++)
{
double t = c_a[k] * b_y1 + c_a[k + 10] * c_idx_1 + dv[k];
a += b_a[k] * t;
}
2. 三阶泰勒展开
for (k = 0; k < 10; k++)
{
double t = c_a[k] * b_y1 + c_a[k + 10] * c_idx_1 + dv[k];
double t_sq = t * t;
a += b_a[k] * (t - t * t_sq / 3.0);
}
3. 五阶泰勒展开(更精确)
for (k = 0; k < 10; k++)
{
double t = c_a[k] * b_y1 + c_a[k + 10] * c_idx_1 + dv[k];
double t_sq = t * t;
double t_fourth = t_sq * t_sq;
a += b_a[k] * (t - t * t_sq / 3.0 + 2.0 * t * t_fourth / 15.0);
}
4. 七阶泰勒展开(高精度)
for (k = 0; k < 10; k++)
{
double t = c_a[k] * b_y1 + c_a[k + 10] * c_idx_1 + dv[k];
double t_sq = t * t;
double t_fourth = t_sq * t_sq;
double t_sixth = t_fourth * t_sq;
a += b_a[k] * (t - t * t_sq / 3.0 + 2.0 * t * t_fourth / 15.0 - 17.0 * t * t_sixth / 315.0);
}
推荐使用
对于大多数应用,五阶展开在精度和计算效率之间提供了良好的平衡:
总结:
-
适用条件 :泰勒展开在
t接近 0 时精度最高,当|t| > 1.5时误差会明显增大 -
性能考虑:原函数包含
exp计算,泰勒展开用多项式替换可以显著提高计算速度 -
精度权衡 :如果
t的范围较大,建议使用五阶或七阶展开,或者保持原函数
你可以根据 t 的典型取值范围选择合适的展开阶数。
四 为什么 exp(x) 在单片机上很慢?
1 原因
(1) 复杂的数学运算
-
exp(x)不是像加减乘除那样的基本指令 -
需要一系列乘、加、除和迭代计算
-
通常通过泰勒展开、查表法或CORDIC算法实现,这些都涉及多次循环和计算
(2) 缺乏硬件支持
-
大多数低端单片机没有硬件浮点单元(FPU)
-
即使有FPU,
exp()也通常不是单指令操作 -
需要软件库实现,计算步骤繁多
(3) 内存和速度限制
-
精确计算需要高精度迭代,消耗大量CPU周期
-
可能还需要存储常数表,占用宝贵的内存
2. 实际性能对比
举个例子,在常见的STM32系列单片机上(无硬件FPU):
| 运算类型 | 大致CPU周期 | 时间 @ 72MHz |
|---|---|---|
| 整数加法 | 1 cycle | ~0.014μs |
| 浮点乘法 | ~20 cycles | ~0.28μs |
exp(x) |
~1000-5000 cycles | ~14-70μs |
可以看到,一次 exp() 计算可能相当于几百次甚至几千次基本运算!
3. 你在原始代码中的情况
你的代码:
c
a += b_a[k] * (2.0 / (exp(-2.0 * t) + 1.0) - 1.0);这实际上是在计算 tanh(t),其中涉及:
-
一次乘法:
-2.0 * t -
一次指数:
exp(...)← 主要瓶颈! -
一次加法:
... + 1.0 -
一次除法:
2.0 / ... -
一次减法:
... - 1.0
指数运算 exp() 消耗了绝大部分计算时间。
4. 解决方案:为什么用泰勒展开
这就是为什么之前建议你用泰勒展开来替换:
原始代码(慢):
c
// 包含昂贵的 exp() 调用
result = 2.0 / (exp(-2.0 * t) + 1.0) - 1.0;泰勒展开(快):
c
// 只用加减乘,没有 exp()
double t3 = t * t * t;
double t5 = t3 * t * t;
result = t - t3/3.0 + 2.0*t5/15.0; // 五阶近似性能提升可能达到10倍甚至100倍!
5. 其他优化方法
除了泰勒展开,还有:
(1) 查表法
c
// 预计算 tanh 值表
const float tanh_table[100] = { ... };
// 使用时直接查表
int index = (int)(t * 10 + 50); // 映射到数组索引
if (index < 0) index = 0;
if (index > 99) index = 99;
result = tanh_table[index];(2) 分段近似
-
小值时用泰勒展开
-
大值时直接返回 ±1(因为 tanh 饱和)
(3) 有理函数近似
用多项式比值来获得更好的精度:
c
// Pade 近似等6. 实际建议
对于你的具体应用:
-
如果
t的范围较小(如 |t| < 2.0):-
使用3阶或5阶泰勒展开
-
在精度和速度间取得良好平衡
-
-
如果需要高精度:
-
使用查表法 + 线性插值
-
或者使用优化的近似公式
-
-
如果性能极其敏感:
-
考虑使用定点数运算代替浮点数
-
使用汇编优化关键部分
-
总结
是的,单片机计算 exp() 等指数运算非常耗时,应该尽量避免在循环或实时处理中使用。泰勒展开、查表法和各种近似方法是嵌入式开发中常用的优化手段。
在你的代码中,用泰勒多项式替换 tanh(t) 可以显著提高运行速度,这是嵌入式优化中的经典技巧!