1 交换左右子树的位置------后序遍历

答案:后序
解析:要交换所有分支结点的左、右子树,需先处理左子树,再处理右子树,最后处理当前结点(交换左、右子树)。后序遍历的顺序是 "左子树→右子树→根结点",符合这一处理逻辑,因此利用后序遍历方法最合适。
2 求最少有多少结点

答案:B
解析:要使结点数最少,需让二叉树每一层的结点尽可能少。因为所有结点的度为 0 或 2,所以第 1 层有 1 个结点(根结点),第 2 层有 2 个结点(根的两个子结点),第 3 层有 2 个结点(第 2 层每个结点的两个子结点)...... 以此类推,第h层有 2 个结点。这是一个等差数列,首项为 1,公差为 1,项数为h,但实际计算时,结点数为\(2h - 1\)。例如,当\(h = 1\)时,结点数为 1,代入\(2h - 1 = 1\),符合;当\(h = 2\)时,结点数为 3,代入\(2h - 1 = 3\),符合。
3 单链状的二叉树
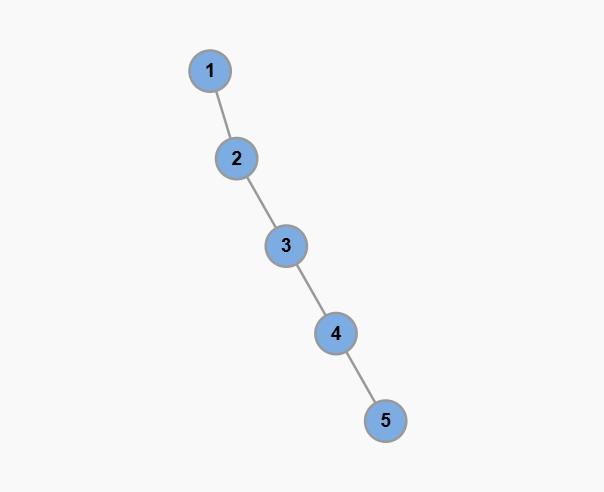
二叉树的定义是**每个结点最多有两个子树(左子树和右子树)的树结构。**
****单链状的二叉树属于斜二叉树,它的每个结点只有左子树或者只有右子树,完全满足二叉树的定义。
比如,一个有 5 个结点的单链状二叉树,每个非叶子结点只有一个子结点,叶子结点没有子结点,这显然符合二叉树的规则。
4 完全二叉树的叶子节点




5 完全二叉树
6 求叶子结点数目

答案:D
解析:设叶子结点数为n_0,根据树的性质 "总结点数 = 总度数 + 1"。
- 总度数为:1×4 + 2×2 + 3×1 + 4×1 = 4 + 4 + 3 + 4 = 15
- 总结点数为:n_0 + 4 + 2 + 1 + 1 = n_0 + 8
- 由 "总结点数 = 总度数 + 1" 可得:n_0 + 8 = 15 + 1,解得n_0 = 8。
7 已知结点数目求完全二叉树深度

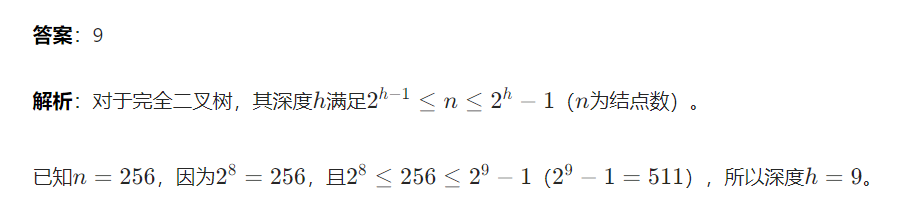
8 n个结点的二叉树空指针数目

答案:√
解析:对于含n个结点的二叉树,每个结点有 2 个指针域(左、右指针),总共有2n个指针域。又因为二叉树中除根结点外,每个结点都有一个指针指向它,所以非空指针数为 n - 1 。因此,空指针数为 2n - (n - 1) = n + 1 ,该说法正确。
9 树和二叉树

答案:×
解析:度为 2 的树是指树中每个结点的度最多为 2,但树的子结点没有左右之分;而二叉树的每个结点的子结点有左、右之分,即使度为 2 的树,其结构也不一定符合二叉树的左右子树定义。因此,度为二的树不一定是二叉树,该说法错误。