文章目录
用代码看见数学之美,让微积分不再枯燥
大家好,我是热爱用Python探索数学奥秘的博主。今天,让我们一起揭秘微积分中一个既实用又有趣的概念------极值。不管是数学小白还是编程新手,都能轻松上手!
什么是极值?生活中的"巅峰"与"低谷"
想象一下你正在爬山。山顶是你能达到的最高点 (极大值),而山谷则是你所在的最低点 (极小值)。在数学中,函数也有这样的"山顶"和"山谷",我们称之为极值点。
极值点就是函数在某点附近达到的局部最大值或最小值点。比如你一天中的能量水平:早上起床是低谷,中午精力充沛达到高峰,下午又有点困倦形成另一个低谷。
那么,如何用Python找到这些点呢?让我们一起来看看吧!
用Python寻找函数的"心情起伏"
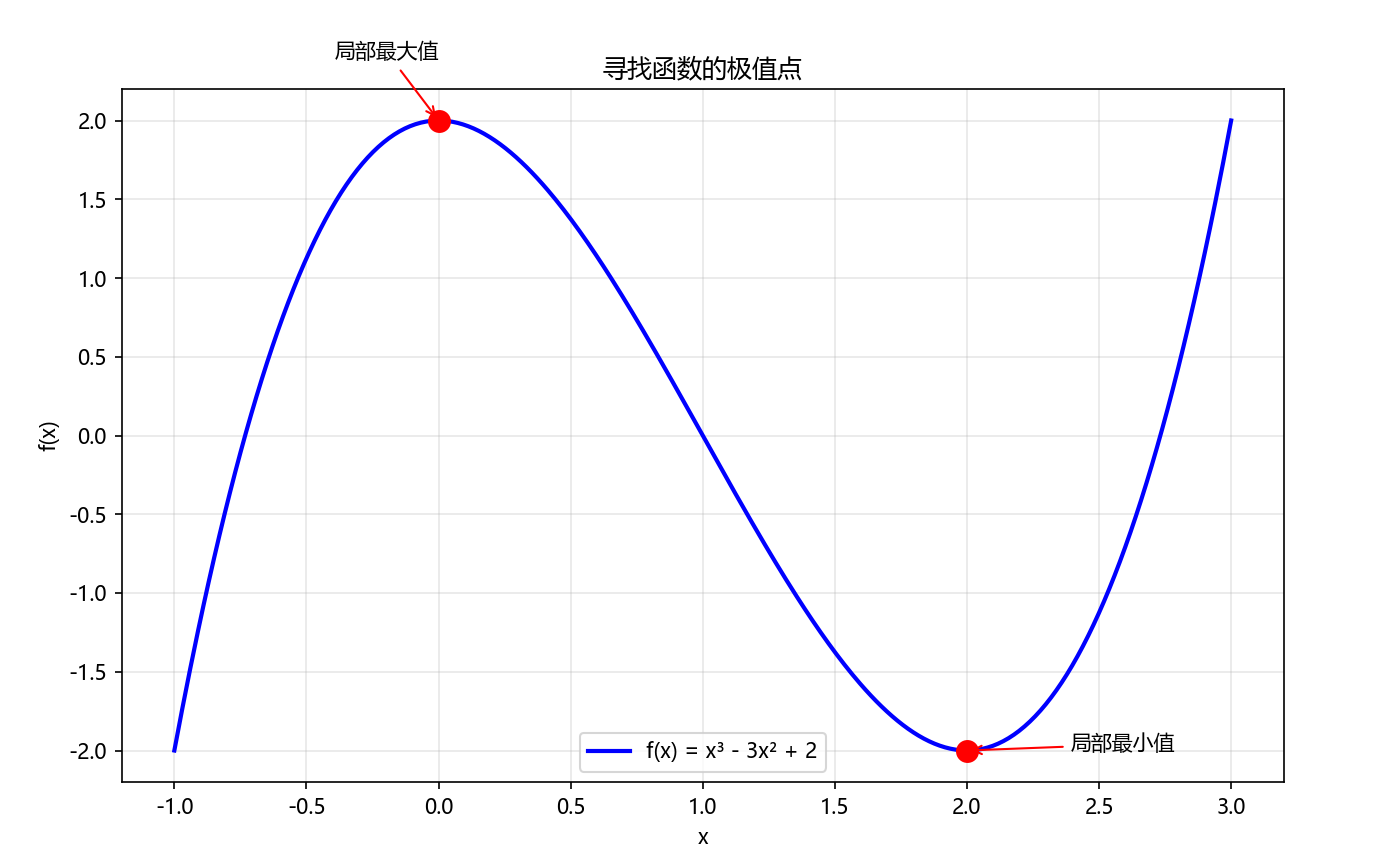
我们先从一个简单的函数开始: f ( x ) = x 3 − 3 x 2 + 2 f(x) = x^3 - 3x^2 + 2 f(x)=x3−3x2+2
python
import numpy as np
import matplotlib.pyplot as plt
from scipy import optimize
# 定义函数
def f(x):
return x**3 - 3*x**2 + 2
# 生成x值(从-1到3,共400个点)
x = np.linspace(-1, 3, 400)
y = f(x)
# 绘制函数图像
plt.figure(figsize=(10, 6))
plt.plot(x, y, 'b-', linewidth=2, label='f(x) = x³ - 3x² + 2')
plt.grid(True, alpha=0.3)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('寻找函数的极值点')
# 标记极值点
extrema_x = [0, 2] # 通过计算我们知道极值点大约在x=0和x=2处
extrema_y = [f(xi) for xi in extrema_x]
plt.scatter(extrema_x, extrema_y, color='red', s=100, zorder=5)
plt.annotate('局部最大值', (0, f(0)), xytext=(-50, 30), textcoords='offset points',
arrowprops=dict(arrowstyle='->', color='red'))
plt.annotate('局部最小值', (2, f(2)), xytext=(50, 0), textcoords='offset points',
arrowprops=dict(arrowstyle='->', color='red'))
plt.legend()
plt.show()当你运行这段代码时,会看到一条蓝色曲线,上面标记了两个红点:一个是局部最大值 (山顶),一个是局部最小值(山谷)。
费马定理:极值点的"交通警察"
法国数学家费马发现了一个有趣的现象:在函数的极值点处,如果函数是光滑的(没有尖角),那么切线是水平的 ,也就是说导数为零。
这就像交通警察在高峰点指挥交通一样,让函数的"变化率"暂时归零!
python
import sympy as sp
# 定义符号变量和函数
x = sp.symbols('x')
f = x**3 - 3*x**2 + 2
# 计算导数
f_prime = sp.diff(f, x)
print("函数f(x)的导数是:", f_prime)
# 求导数为零的点(临界点)
critical_points = sp.solve(f_prime, x)
print("临界点是:", critical_points)
# 判断这些点是极大值还是极小值
for point in critical_points:
# 计算二阶导数
f_double_prime = sp.diff(f_prime, x)
second_deriv_value = f_double_prime.subs(x, point)
if second_deriv_value > 0:
print(f"x={point}是局部极小值点")
elif second_deriv_value < 0:
print(f"x={point}是局部极大值点")
else:
print(f"x={point}可能是拐点")运行结果:

极值在现实世界中的应用
极值概念不仅在数学中重要,在现实生活中也有广泛应用:
- 经济学:寻找利润最大化和成本最小化的方案
- 工程学:设计最节省材料的结构
- 数据科学:机器学习中的优化算法核心就是寻找极值
- 日常生活:寻找上班最短路径、投资最大回报等
动手试一试:发现你函数的"个性"
现在轮到你了!尝试修改上面代码中的函数定义,比如改成:
- f ( x ) = x 4 − 4 x 2 f(x) = x^4 - 4x^2 f(x)=x4−4x2(一个更"起伏"的函数)
- f ( x ) = sin ( x ) f(x) = \sin(x) f(x)=sin(x)(波浪形函数)
- 你自己设计的任何函数!
观察与思考:
- 你发现的极值点在哪里?
- 是极大值还是极小值?
- 如果你改变函数,极值点会如何移动?
互动时间:分享你的发现!
微积分不应该是枯燥的公式和定理,而是探索世界的有趣工具。通过Python,我们能让这些抽象概念变得直观可见!
欢迎在评论区分享:
- 你运行代码后的发现和感想
- 你遇到的理解难点或有趣现象
- 你想了解的下一个微积分主题
如果觉得这篇博文对你有帮助,请:
- 点赞让我知道你喜欢这种教学方式
- 关注以免错过后续的Python与数学系列
- 分享给可能感兴趣的朋友
小问题:你能想到生活中还有哪些"极值"的例子吗?在评论区告诉我吧!
往期精彩回顾:
专栏导航目录 《程序员AI之路:从Python起步》完全学习导航
完整代码已开源 ai-learning-path,欢迎Star和Fork!
下期预告:在下一篇文章中,我们将开始学习微分中值定理,包括费马定理、罗马定理、拉格朗日定理等。
参考资料:
- 扈志明《微积分》教材
互动邀请:如果你对本章内容有独特的理解或在实际应用中遇到过有趣的问题,欢迎在评论区分享交流!