C语言 . 第三章第二节 .递归函数

递归是一类编程技巧

一、阶乘函数

我们以阶乘函数为例，感受一下递归的流程

c 复制代码

#include<stdio.h>

int f(int n) {
    printf("in f(%d)\n", n);
    int ret;
    if (n == 1) ret = 1;
    else ret = n * f(n - 1);
    printf("out f(%d)\n", n);
    return ret;
}

int main() {
    int n;
    while (scanf("%d", &n) ！= EOF) {
        printf("f(%d) = %d\n", n, f(n));
    }
    return 0;
}

效果：

具体流程：（转载自@初猿°）

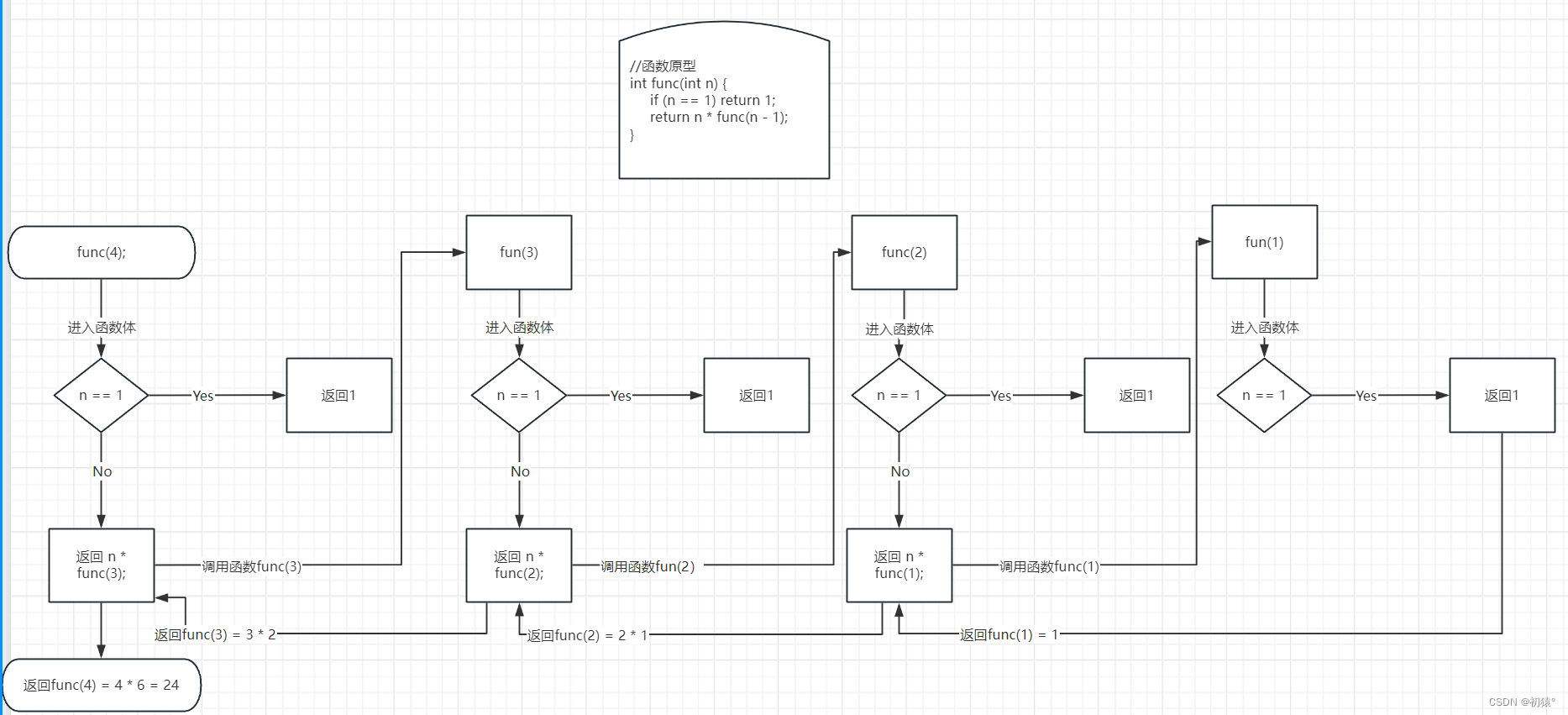
二、斐波那契数列

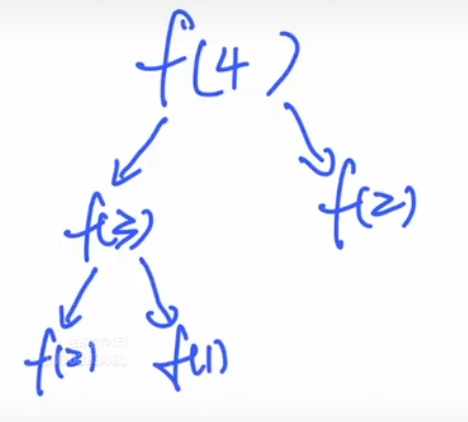
在演算递归过程时，我们可以画树状图简化过程。

以计算f（4）为例，先递归向下，再递归向上

三、设计一个递归函数

1、欧几里得算法------最大公约数

整数a，b的最大公约数一般表示为gcd(a,b);

最大公约数，就是a和b同时能整除的最大的数字, 比如32和24的最大公约数是8;

最终式子:gcd(a,b) = gcd(b, a % b)

复制代码

    解释：gcd(a,b)返回值就是a和b的最大公约数

    现在需要证明: 
    命题1. b 和 a % b的最大公约数是 a 和 b 的公约数。
    
    命题2. b 和 a % b的最大公约数也是 a 和 b 的最大公约数

证明1：

typescript 复制代码

设 gcd (b, a % b) = c 
由于 b 是 c 的倍数，不妨设 b = xc -----（i）
同理（a % b）（a / b 的余数）是 c 的倍数，设 a - kb = yc
移项可得 a = （y + kx）* c-------------（ii）
对比（i）式和（ii）式
可知 a 和 b 的公约数也是c
证毕！

证明2：

typescript 复制代码

证明1中有个隐含条件：x 与 y 互质
反证：
若x， y公约数，则 c 不是那两者的最大公约数，矛盾。
故 x，y 互质，则 gcd （x，y）= 1-----（iii）
-------------------------------------
要证明命题2，即证 x 与 y + kx 互质
反证：
若其不互质，则设gcd（x，y + kx）= d （d ！= 1）
x = nd
y + kx = md---->y = (m - kn)* d
由此，我们得出gcd（x，y）= d
又由式（iii），得 d = 1，这与 d ！= 1矛盾
故 x 与 y + kx 互质
证毕！

代码实现欧几里得算法：

c 复制代码

#include<stdio.h>


int gcd(int a, int b) {
    if (b == 0) return a;//边界条件
    return gcd(b, a % b);
}


int main(){
    int a, b;
    while (scanf("%d%d", &a, &b) != EOF) {
        printf("gcd(%d, %d) = %d\n", a, b, gcd(a, b));
    }
    return 0;
}

效果：

2、"被忽视的"递归函数

除了main函数之外的函数都无法动用！

怎么办？

我们先不管能不能用，先用递归函数设计一个先

c 复制代码

#include<stdio.h>
//不需要返回值就定义void类型
void printf_function(int current, int end);//设定开始值和终点值

int main(){
    printf_function(1, 100);//调用函数时只需：函数名+（参数列表）
    printf("\n");
    return 0;
}

void printf_function(int current, int end){
    //第一步：检查终止条件
    if (current > end)        
        return; //如果当前值超过结束值，就停止

    //第二步：执行当前任务
    printf("%d ", current);

    //第三步：递归调用（向终止条件靠近）
    printf_function(current + 1, end);
}

可惜我们并不符合要求。

但是如果我们把main函数改造成递归函数呢？

c 复制代码

#include<stdio.h>

int k = 100;//定义一个全局变量，用于运算和赋值
int main(){
    int n = k; //k负责运算和赋值，n用于判断和打印
    k -= 1;
    if (n == 1){
        printf("%d\n", n);
        return 0;//注意if语句不能用break结束！！！
    }
    main();//main函数调用自身
    printf("%d\n", n);
    return 0;
}

完美通过