目录
[① MDH参数](#① MDH参数)
[① MDH参数](#① MDH参数)
一、数学建模
(1)Matlab中PUMA560六自由度机械臂正反解,博客连接:https://blog.csdn.net/panjinliang066333/article/details/121681602?spm=1011.2415.3001.5331
(2)机械臂动画示意图,见博客:https://blog.csdn.net/panjinliang066333/article/details/141264547?spm=1011.2415.3001.5331
(3)PUMA560六自由度机械臂,关节示意图说明

模型示意图
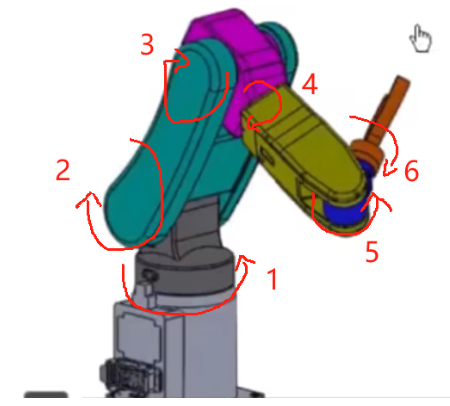
实物示意图
1、连杆定义
备注:文档介绍说明,引用教材《机器人学》-蔡自兴

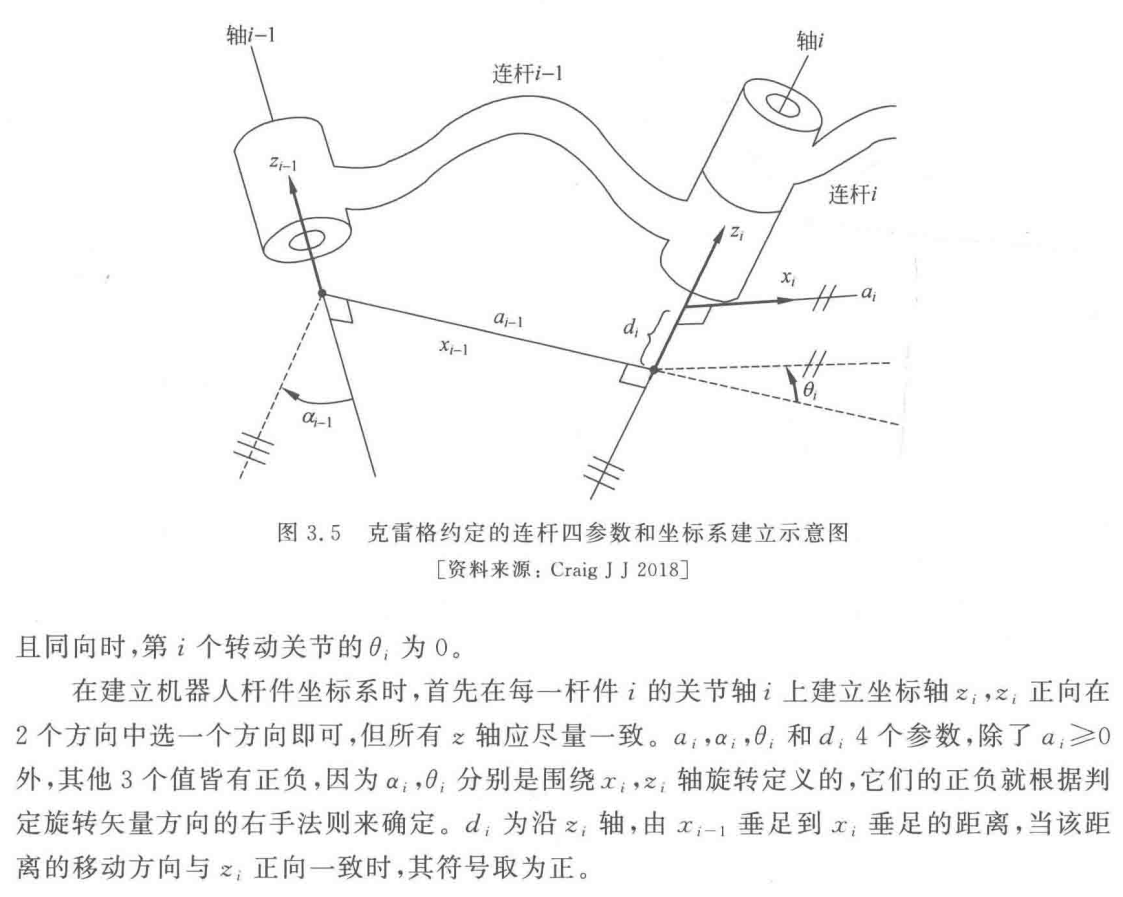
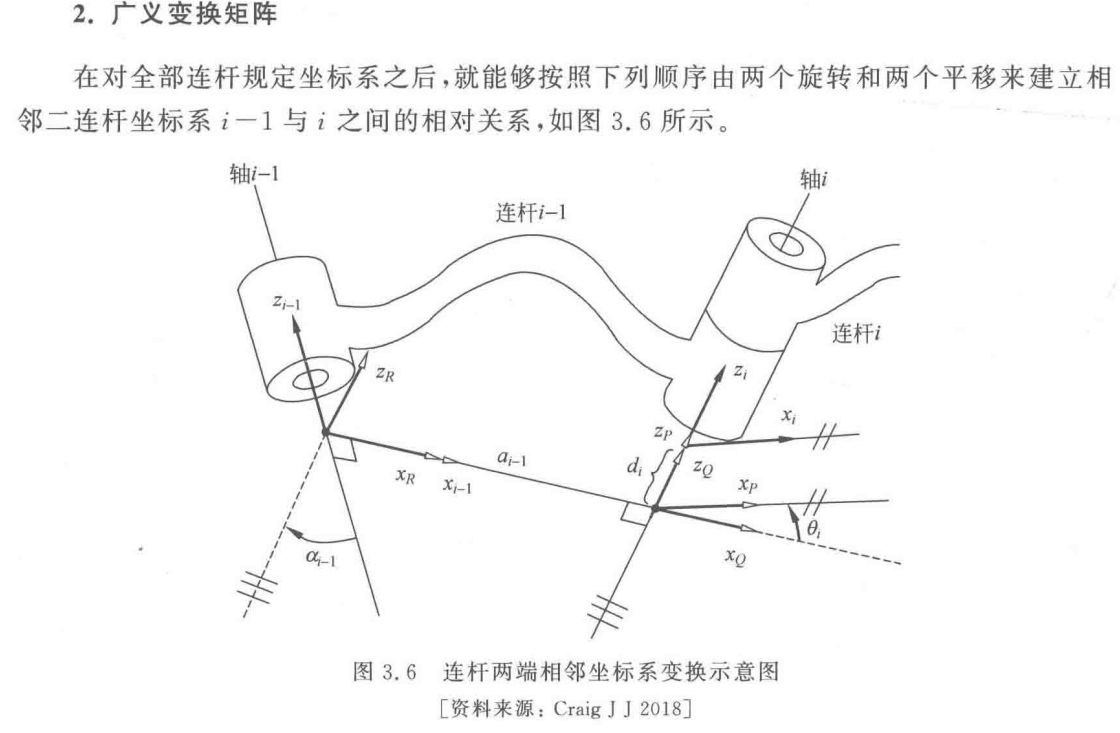

2、建立连杆坐标系的步骤和举例
(1)步骤说明


(2)举例说明

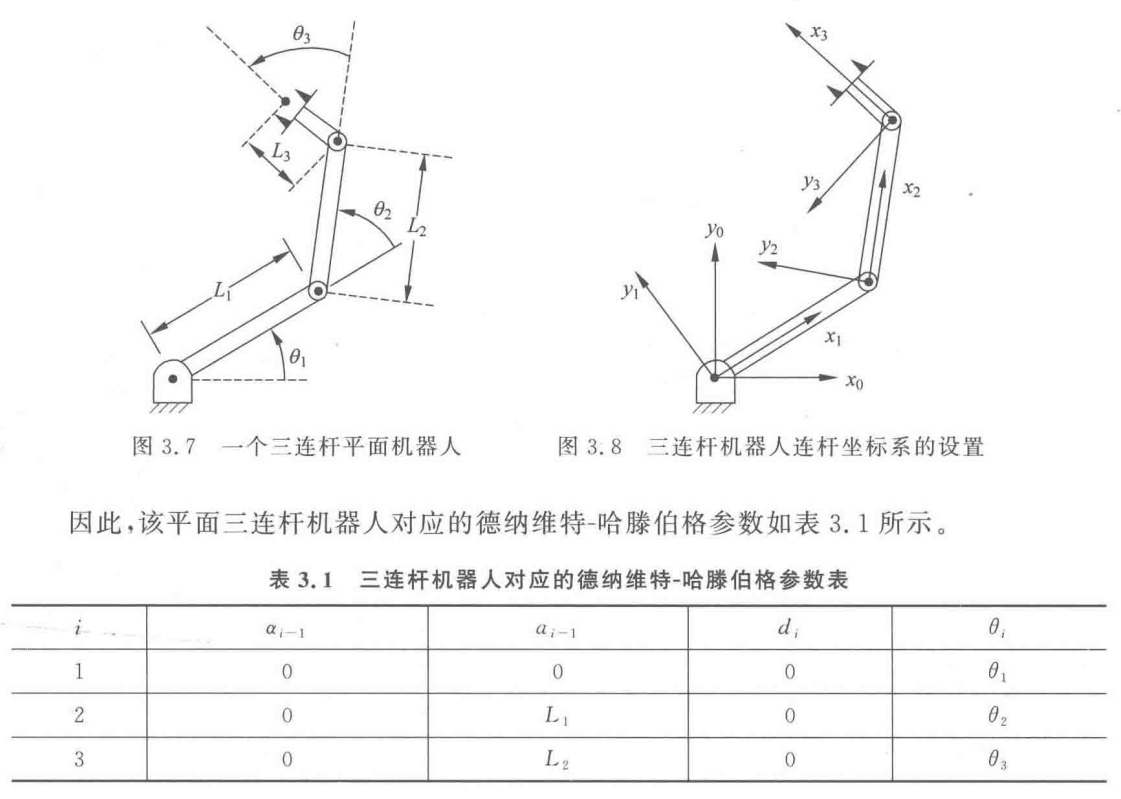
3、PUMA560串联机械臂建模
(1)各关节和坐标系建立
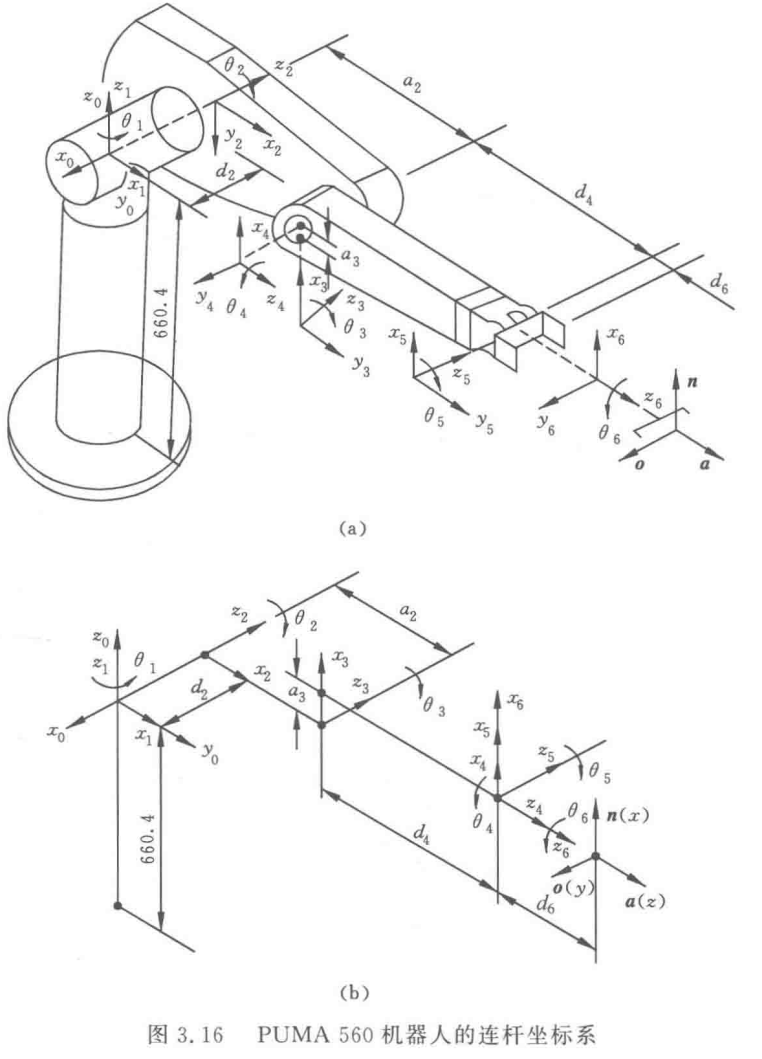
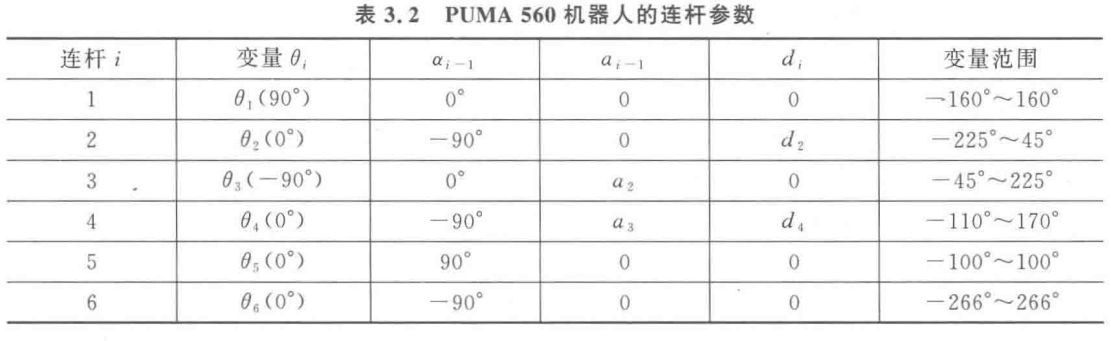
(2)正解计算各关节矩阵如下

则末关节矩阵:
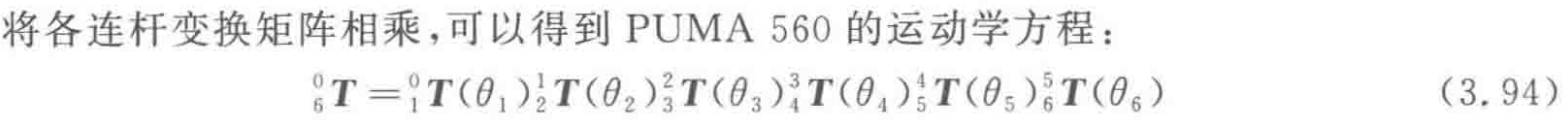
(3)逆解计算如下








多个解情况

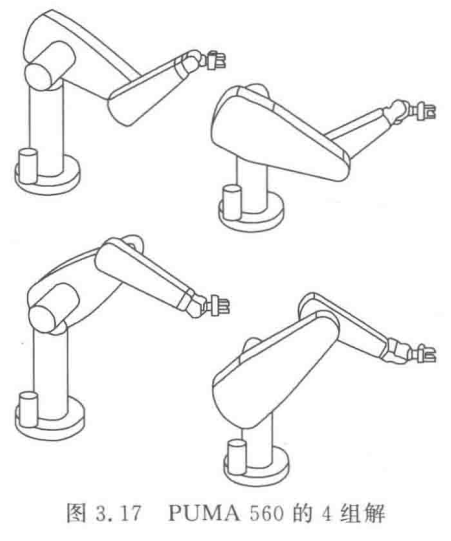
二、C#程序实现
1、软件界面
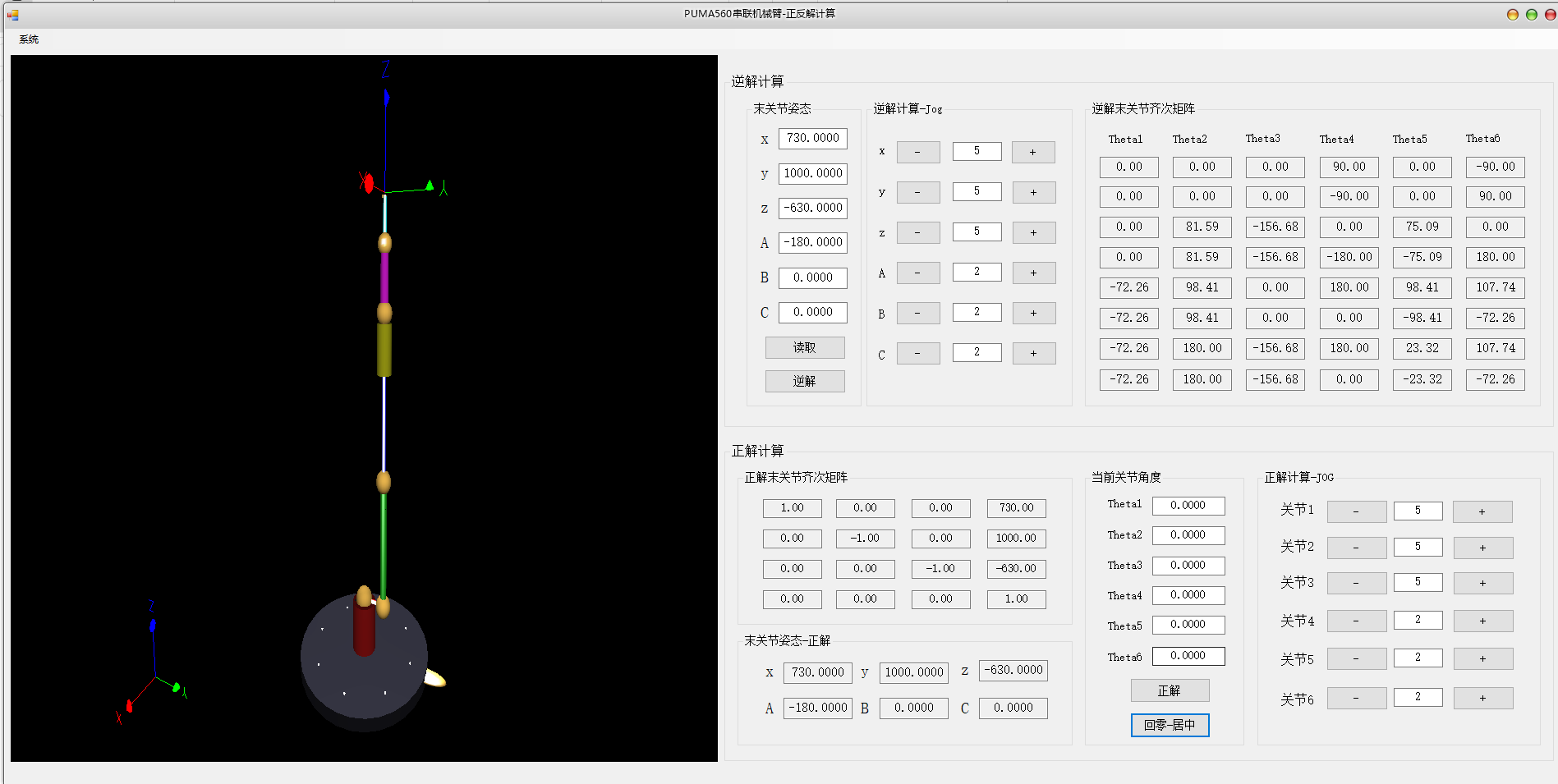
主界面-初始
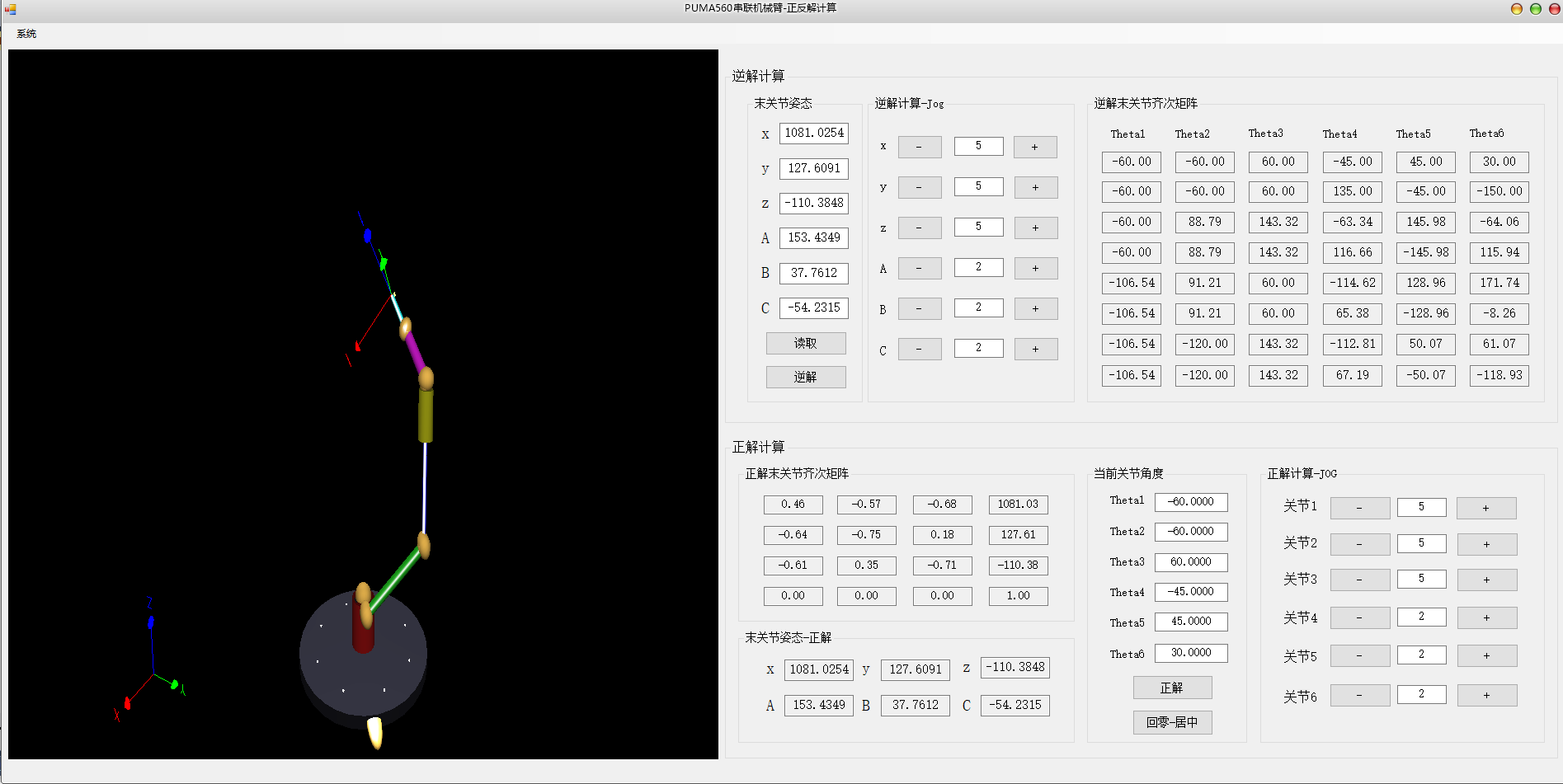
主界面-运行
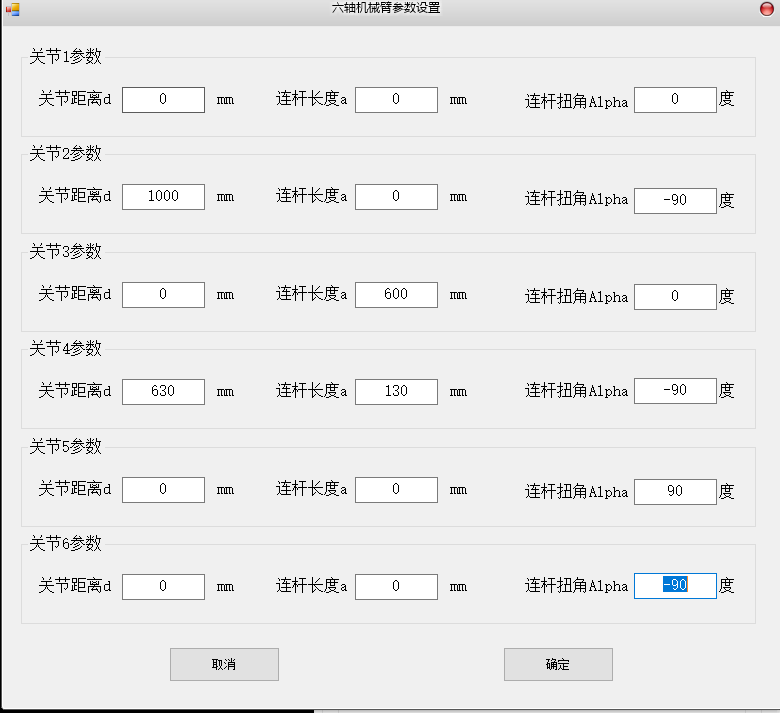
参数设置
2、关键功能代码实现
(1)UI中绘制机械臂
机械臂如上面主界面图片所示,使用SharpGL库文件在Winform中,绘制具有工业风格的六轴机械臂
代码
public void DrawRobot1(ref OpenGL gl, float[] angle, float[] yLength, bool isPuma560_Six)
{
// 开启深度测试和光照
gl.Enable(OpenGL.GL_DEPTH_TEST);
gl.Enable(OpenGL.GL_LIGHTING);
gl.Enable(OpenGL.GL_LIGHT0);
gl.Enable(OpenGL.GL_LIGHT1);
gl.ShadeModel(OpenGL.GL_SMOOTH);
// 设置更强的光源
float[] light0Pos = { 20.0f, 30.0f, 40.0f, 1.0f };
float[] light0Ambient = { 0.4f, 0.4f, 0.4f, 1.0f };
float[] light0Diffuse = { 1.0f, 1.0f, 1.0f, 1.0f };
float[] light0Specular = { 1.0f, 1.0f, 1.0f, 1.0f };
float[] light1Pos = { -20.0f, 20.0f, -30.0f, 1.0f };
float[] light1Ambient = { 0.2f, 0.2f, 0.2f, 1.0f };
float[] light1Diffuse = { 0.6f, 0.6f, 0.6f, 1.0f };
gl.Light(OpenGL.GL_LIGHT0, OpenGL.GL_POSITION, light0Pos);
gl.Light(OpenGL.GL_LIGHT0, OpenGL.GL_AMBIENT, light0Ambient);
gl.Light(OpenGL.GL_LIGHT0, OpenGL.GL_DIFFUSE, light0Diffuse);
gl.Light(OpenGL.GL_LIGHT0, OpenGL.GL_SPECULAR, light0Specular);
gl.Light(OpenGL.GL_LIGHT1, OpenGL.GL_POSITION, light1Pos);
gl.Light(OpenGL.GL_LIGHT1, OpenGL.GL_AMBIENT, light1Ambient);
gl.Light(OpenGL.GL_LIGHT1, OpenGL.GL_DIFFUSE, light1Diffuse);
// 设置材质属性
gl.Material(OpenGL.GL_FRONT, OpenGL.GL_AMBIENT, matAmbient);
gl.Material(OpenGL.GL_FRONT, OpenGL.GL_DIFFUSE, matDiffuse);
gl.Material(OpenGL.GL_FRONT, OpenGL.GL_SPECULAR, matSpecular);
gl.Material(OpenGL.GL_FRONT, OpenGL.GL_SHININESS, matShininess);
// 绘制机器人底座
DrawBase(ref gl, yLength[0]);
// 在基座左下角绘制固定的世界坐标系
DrawFixedWorldCoordinateSystem(ref gl, yLength[0]);
// 绘制底座与第一关节的连接器
gl.PushMatrix();
gl.Translate(0.0f, -yLength[0] / 2, 0.0f);
DrawBaseToJoint1Connector(ref gl);
gl.PopMatrix();
// 第一关节 - 绕Y轴旋转
gl.PushMatrix();
{
gl.Translate(0.0f, -yLength[0] / 2, 0.0f);
gl.Rotate(angle[0], 0.0f, 1.0f, 0.0f);
DrawJoint1(ref gl, yLength[0]);
}
gl.PopMatrix();
// 第二关节 - 绕X轴旋转
gl.PushMatrix();
{
gl.Translate(0.0f, -yLength[0] / 2, 0.0f);
gl.Rotate(angle[0], 0.0f, 1.0f, 0.0f);
gl.Translate(2.5f, yLength[0] / 2, 0.0f);
gl.Rotate(angle[1], 1.0f, 0.0f, 0.0f);
// 注意:关节2现在从关节1的圆柱末端开始
DrawJoint2(ref gl, yLength[1]);
}
gl.PopMatrix();
// 第三关节 - 绕X轴旋转
gl.PushMatrix();
{
gl.Translate(0.0f, -yLength[0] / 2, 0.0f);
gl.Rotate(angle[0], 0.0f, 1.0f, 0.0f);
gl.Translate(2.5f, yLength[0] / 2, 0.0f);
gl.Rotate(angle[1], 1.0f, 0.0f, 0.0f);
gl.Translate(0.0f, yLength[1], 0.0f);
gl.Rotate(angle[2], 1.0f, 0.0f, 0.0f);
DrawJoint3(ref gl, yLength[2]);
}
gl.PopMatrix();
// 第四关节 - 绕Y轴旋转
gl.PushMatrix();
{
gl.Translate(0.0f, -yLength[0] / 2, 0.0f);
gl.Rotate(angle[0], 0.0f, 1.0f, 0.0f);
gl.Translate(2.5f, yLength[0] / 2, 0.0f);
gl.Rotate(angle[1], 1.0f, 0.0f, 0.0f);
gl.Translate(0.0f, yLength[1], 0.0f);
gl.Rotate(angle[2], 1.0f, 0.0f, 0.0f);
gl.Translate(0.0f, yLength[2], 0.0f);
gl.Rotate(angle[3], 0.0f, 1.0f, 0.0f);
DrawJoint4(ref gl, yLength[3]);
}
gl.PopMatrix();
if (isPuma560_Six)
{
// 第五关节 - 绕X轴旋转
gl.PushMatrix();
{
gl.Translate(0.0f, -yLength[0] / 2, 0.0f);
gl.Rotate(angle[0], 0.0f, 1.0f, 0.0f);
gl.Translate(2.5f, yLength[0] / 2, 0.0f);
gl.Rotate(angle[1], 1.0f, 0.0f, 0.0f);
gl.Translate(0.0f, yLength[1], 0.0f);
gl.Rotate(angle[2], 1.0f, 0.0f, 0.0f);
gl.Translate(0.0f, yLength[2], 0.0f);
gl.Rotate(angle[3], 0.0f, 1.0f, 0.0f);
gl.Translate(0.0f, yLength[3], 0.0f);
gl.Rotate(angle[4], 1.0f, 0.0f, 0.0f);
// 注意:关节5现在从关节4的球体顶部开始
DrawJoint5(ref gl, yLength[4]);
}
gl.PopMatrix();
// 第六关节 - 绕Y轴旋转 + 末端坐标系
gl.PushMatrix();
{
gl.Translate(0.0f, -yLength[0] / 2, 0.0f);
gl.Rotate(angle[0], 0.0f, 1.0f, 0.0f);
gl.Translate(2.5f, yLength[0] / 2, 0.0f);
gl.Rotate(angle[1], 1.0f, 0.0f, 0.0f);
gl.Translate(0.0f, yLength[1], 0.0f);
gl.Rotate(angle[2], 1.0f, 0.0f, 0.0f);
gl.Translate(0.0f, yLength[2], 0.0f);
gl.Rotate(angle[3], 0.0f, 1.0f, 0.0f);
gl.Translate(0.0f, yLength[3], 0.0f);
gl.Rotate(angle[4], 1.0f, 0.0f, 0.0f);
gl.Translate(0.0f, yLength[4], 0.0f);
gl.Rotate(angle[5], 0.0f, 1.0f, 0.0f);
DrawJoint6(ref gl, yLength[5]);
}
gl.PopMatrix();
}
// 绘制世界坐标系
DrawWorldCoordinateSystem(ref gl);
gl.Disable(OpenGL.GL_LIGHTING);
}(2)正解计算
① MDH参数
/// <summary>
/// 构造函数,内部默认MDH参数
/// </summary>
public Puma560FK()
{
_mdhParams = new double[,]
{
//[ d, a, alpha]
{ 0, 0, 0 },
{ 0, 0.180, -Math.PI/2 },
{ 0, 0.600, 0 },
{ 0.630, 0.130, -Math.PI/2 },
{ 0, 0, Math.PI/2 },
{ 0, 0, -Math.PI/2 }
};
}
/// <summary>
/// 构造函数,外部输入MDH参数
/// </summary>
/// <param name="mdhParameters"></param>
public Puma560FK(double[,] mdhParameters)
{
if (mdhParameters == null)
throw new ArgumentNullException("mdhParameters");
if (mdhParameters.GetLength(0) != 6 || mdhParameters.GetLength(1) != 3)
throw new ArgumentException("MDH参数必须是6x4矩阵");
_mdhParams = (double[,])mdhParameters.Clone();
}②正解计算
/// <summary>
/// 计算机器人末端位姿(齐次变换矩阵)
/// </summary>
/// <param name="theta">6个关节角度数组(弧度)</param>
/// <returns>4x4齐次变换矩阵</returns>
public double[,] ForwardKinematics(double[] theta)
{
if (theta == null || theta.Length != 6)
throw new ArgumentException("需要6个关节角度参数");
// 计算各关节变换矩阵
double[,] T01 = CalculateTransform(theta[0] * Math.PI / 180.0f, _mdhParams[0, 0], _mdhParams[0, 1], _mdhParams[0, 2]);
double[,] T12 = CalculateTransform(theta[1] * Math.PI / 180.0f, _mdhParams[1, 0], _mdhParams[1, 1], _mdhParams[1, 2]);
double[,] T23 = CalculateTransform(theta[2] * Math.PI / 180.0f, _mdhParams[2, 0], _mdhParams[2, 1], _mdhParams[2, 2]);
double[,] T34 = CalculateTransform(theta[3] * Math.PI / 180.0f, _mdhParams[3, 0], _mdhParams[3, 1], _mdhParams[3, 2]);
double[,] T45 = CalculateTransform(theta[4] * Math.PI / 180.0f, _mdhParams[4, 0], _mdhParams[4, 1], _mdhParams[4, 2]);
double[,] T56 = CalculateTransform(theta[5] * Math.PI / 180.0f, _mdhParams[5, 0], _mdhParams[5, 1], _mdhParams[5, 2]);
// 级联变换矩阵
double[,] T02 = MatrixMultiply(T01, T12);
double[,] T03 = MatrixMultiply(T02, T23);
double[,] T04 = MatrixMultiply(T03, T34);
double[,] T05 = MatrixMultiply(T04, T45);
double[,] T06 = MatrixMultiply(T05, T56);
return T06;
}(3)逆解计算
① MDH参数
MDH = new double[,]
{
//[ d, a-1, alpha-1 ]
{ 0, 0, 0 },
{ 0, 0.180, -Math.PI/2 },
{ 0, 0.600, 0 },
{ 0.630, 0.130, -Math.PI/2 },
{ 0, 0, Math.PI/2 },
{ 0, 0, -Math.PI/2 }
};
}
/// <summary>
/// 构造函数,外部输入MDH参数
/// </summary>
/// <param name="mdhParameters"></param>
public Puma560IK(double[,] mdhParameters)
{
if (mdhParameters == null)
throw new ArgumentNullException("mdhParameters");
if (mdhParameters.GetLength(0) != 6 || mdhParameters.GetLength(1) != 3)
throw new ArgumentException("MDH参数必须是6x3矩阵");
MDH = (double[,])mdhParameters.Clone();
}②逆解计算
public double[,] ComputeIK(double[,] Tbe)
{
// Extract position and orientation components from transformation matrix
double nx = Tbe[0, 0], ny = Tbe[1, 0], nz = Tbe[2, 0];
double ox = Tbe[0, 1], oy = Tbe[1, 1], oz = Tbe[2, 1];
double ax = Tbe[0, 2], ay = Tbe[1, 2], az = Tbe[2, 2];
double px = Tbe[0, 3], py = Tbe[1, 3], pz = Tbe[2, 3];
//// Extract MDH parameters from the 6x3 matrix
//double d4 = MDH[3, 0];
//double a1 = MDH[1, 1];
//double a2 = MDH[2, 1];
//double a3 = MDH[3, 1];
//double d2 = 0, d3 = 0; // These are zero in the MDH table
//// Extract alpha angles from MDH
//double f1 = MDH[1, 2]; // alpha1
//double f3 = MDH[3, 2]; // alpha3
//double f4 = MDH[4, 2]; // alpha4
//double f5 = MDH[5, 2]; // alpha5
double d1 = MDH[0, 0];
double d2 = MDH[1, 0];
double d3 = MDH[2, 0];
double d4 = MDH[3, 0];
double d5 = MDH[4, 0];
double d6 = MDH[5, 0];
double a1 = MDH[1, 1];
double a2 = MDH[2, 1];
double a3 = MDH[3, 1];
double a4 = MDH[4, 1];
double a5 = MDH[5, 1];
double f1 = MDH[1, 2]; // alpha1
double f2 = MDH[2, 2]; // alpha2
double f3 = MDH[3, 2]; // alpha3
double f4 = MDH[4, 2]; // alpha4
double f5 = MDH[5, 2]; // alpha5
// Calculate theta1 solutions
double t11 = -Math.Atan2(-py, px) + Math.Atan2((d2 - d3) / Math.Sin(f1),
Math.Sqrt(Math.Pow(px * Math.Sin(f1), 2) + Math.Pow(py * Math.Sin(f1), 2) - Math.Pow(d2 - d3, 2)));
double t12 = -Math.Atan2(-py, px) + Math.Atan2((d2 - d3) / Math.Sin(f1),
-Math.Sqrt(Math.Pow(px * Math.Sin(f1), 2) + Math.Pow(py * Math.Sin(f1), 2) - Math.Pow(d2 - d3, 2)));
// Calculate intermediate values for theta3
double m3_1 = pz * Math.Sin(f1);
double n3_1 = a1 - px * Math.Cos(t11) - py * Math.Sin(t11);
double m3_2 = pz * Math.Sin(f1);
double n3_2 = a1 - px * Math.Cos(t12) - py * Math.Sin(t12);
// Calculate theta3 solutions
double t31 = -Math.Atan2(a2 * a3 / Math.Sin(f3), a2 * d4) +
Math.Atan2((Math.Pow(m3_1, 2) + Math.Pow(n3_1, 2) - Math.Pow(a2, 2) - Math.Pow(a3, 2) - Math.Pow(d4, 2)) / Math.Sin(f3),
Math.Sqrt(Math.Pow(2 * a2 * d4 * Math.Sin(f3), 2) + Math.Pow(2 * a2 * a3, 2) -
Math.Pow(Math.Pow(m3_1, 2) + Math.Pow(n3_1, 2) - Math.Pow(a2, 2) - Math.Pow(a3, 2) - Math.Pow(d4, 2), 2)));
double t32 = -Math.Atan2(a2 * a3 / Math.Sin(f3), a2 * d4) +
Math.Atan2((Math.Pow(m3_1, 2) + Math.Pow(n3_1, 2) - Math.Pow(a2, 2) - Math.Pow(a3, 2) - Math.Pow(d4, 2)) / Math.Sin(f3),
-Math.Sqrt(Math.Pow(2 * a2 * d4 * Math.Sin(f3), 2) + Math.Pow(2 * a2 * a3, 2) -
Math.Pow(Math.Pow(m3_1, 2) + Math.Pow(n3_1, 2) - Math.Pow(a2, 2) - Math.Pow(a3, 2) - Math.Pow(d4, 2), 2)));
double t33 = -Math.Atan2(a2 * a3 / Math.Sin(f3), a2 * d4) +
Math.Atan2((Math.Pow(m3_2, 2) + Math.Pow(n3_2, 2) - Math.Pow(a2, 2) - Math.Pow(a3, 2) - Math.Pow(d4, 2)) / Math.Sin(f3),
Math.Sqrt(Math.Pow(2 * a2 * d4 * Math.Sin(f3), 2) + Math.Pow(2 * a2 * a3, 2) -
Math.Pow(Math.Pow(m3_2, 2) + Math.Pow(n3_2, 2) - Math.Pow(a2, 2) - Math.Pow(a3, 2) - Math.Pow(d4, 2), 2)));
double t34 = -Math.Atan2(a2 * a3 / Math.Sin(f3), a2 * d4) +
Math.Atan2((Math.Pow(m3_2, 2) + Math.Pow(n3_2, 2) - Math.Pow(a2, 2) - Math.Pow(a3, 2) - Math.Pow(d4, 2)) / Math.Sin(f3),
-Math.Sqrt(Math.Pow(2 * a2 * d4 * Math.Sin(f3), 2) + Math.Pow(2 * a2 * a3, 2) -
Math.Pow(Math.Pow(m3_2, 2) + Math.Pow(n3_2, 2) - Math.Pow(a2, 2) - Math.Pow(a3, 2) - Math.Pow(d4, 2), 2)));
// Calculate intermediate values for theta2
double m2_1 = a2 + a3 * Math.Cos(t31) + d4 * Math.Sin(f3) * Math.Sin(t31);
double n2_1 = a3 * Math.Sin(t31) - d4 * Math.Sin(f3) * Math.Cos(t31);
double m2_2 = a2 + a3 * Math.Cos(t32) + d4 * Math.Sin(f3) * Math.Sin(t32);
double n2_2 = a3 * Math.Sin(t32) - d4 * Math.Sin(f3) * Math.Cos(t32);
double m2_3 = a2 + a3 * Math.Cos(t33) + d4 * Math.Sin(f3) * Math.Sin(t33);
double n2_3 = a3 * Math.Sin(t33) - d4 * Math.Sin(f3) * Math.Cos(t33);
double m2_4 = a2 + a3 * Math.Cos(t34) + d4 * Math.Sin(f3) * Math.Sin(t34);
double n2_4 = a3 * Math.Sin(t34) - d4 * Math.Sin(f3) * Math.Cos(t34);
// Calculate theta2 solutions
double t21 = Math.Atan2(m3_1 * m2_1 + n2_1 * n3_1, m3_1 * n2_1 - m2_1 * n3_1);
double t22 = Math.Atan2(m3_1 * m2_2 + n2_2 * n3_1, m3_1 * n2_2 - m2_2 * n3_1);
double t23 = Math.Atan2(m3_2 * m2_3 + n2_3 * n3_2, m3_2 * n2_3 - m2_3 * n3_2);
double t24 = Math.Atan2(m3_2 * m2_4 + n2_4 * n3_2, m3_2 * n2_4 - m2_4 * n3_2);
// Calculate intermediate values for theta5
double m5_1 = -Math.Sin(f5) * (ax * Math.Cos(t11) * Math.Cos(t21) + ay * Math.Sin(t11) * Math.Cos(t21) + az * Math.Sin(f1) * Math.Sin(t21));
double n5_1 = Math.Sin(f5) * (ax * Math.Cos(t11) * Math.Sin(t21) + ay * Math.Sin(t11) * Math.Sin(t21) - az * Math.Sin(f1) * Math.Cos(t21));
double m5_2 = -Math.Sin(f5) * (ax * Math.Cos(t11) * Math.Cos(t22) + ay * Math.Sin(t11) * Math.Cos(t22) + az * Math.Sin(f1) * Math.Sin(t22));
double n5_2 = Math.Sin(f5) * (ax * Math.Cos(t11) * Math.Sin(t22) + ay * Math.Sin(t11) * Math.Sin(t22) - az * Math.Sin(f1) * Math.Cos(t22));
double m5_3 = -Math.Sin(f5) * (ax * Math.Cos(t12) * Math.Cos(t23) + ay * Math.Sin(t12) * Math.Cos(t23) + az * Math.Sin(f1) * Math.Sin(t23));
double n5_3 = Math.Sin(f5) * (ax * Math.Cos(t12) * Math.Sin(t23) + ay * Math.Sin(t12) * Math.Sin(t23) - az * Math.Sin(f1) * Math.Cos(t23));
double m5_4 = -Math.Sin(f5) * (ax * Math.Cos(t12) * Math.Cos(t24) + ay * Math.Sin(t12) * Math.Cos(t24) + az * Math.Sin(f1) * Math.Sin(t24));
double n5_4 = Math.Sin(f5) * (ax * Math.Cos(t12) * Math.Sin(t24) + ay * Math.Sin(t12) * Math.Sin(t24) - az * Math.Sin(f1) * Math.Cos(t24));
// Calculate theta5 solutions
double t51 = Math.Atan2(Math.Sqrt(Math.Pow(ay * Math.Cos(t11) - ax * Math.Sin(t11), 2) +
Math.Pow(m5_1 * Math.Cos(t31) + n5_1 * Math.Sin(t31), 2)),
(m5_1 * Math.Sin(t31) - n5_1 * Math.Cos(t31)) / (Math.Sin(f3) * Math.Sin(f4)));
double t52 = Math.Atan2(-Math.Sqrt(Math.Pow(ay * Math.Cos(t11) - ax * Math.Sin(t11), 2) +
Math.Pow(m5_1 * Math.Cos(t31) + n5_1 * Math.Sin(t31), 2)),
(m5_1 * Math.Sin(t31) - n5_1 * Math.Cos(t31)) / (Math.Sin(f3) * Math.Sin(f4)));
double t53 = Math.Atan2(Math.Sqrt(Math.Pow(ay * Math.Cos(t11) - ax * Math.Sin(t11), 2) +
Math.Pow(m5_2 * Math.Cos(t32) + n5_2 * Math.Sin(t32), 2)),
(m5_2 * Math.Sin(t32) - n5_2 * Math.Cos(t32)) / (Math.Sin(f3) * Math.Sin(f4)));
double t54 = Math.Atan2(-Math.Sqrt(Math.Pow(ay * Math.Cos(t11) - ax * Math.Sin(t11), 2) +
Math.Pow(m5_2 * Math.Cos(t32) + n5_2 * Math.Sin(t32), 2)),
(m5_2 * Math.Sin(t32) - n5_2 * Math.Cos(t32)) / (Math.Sin(f3) * Math.Sin(f4)));
double t55 = Math.Atan2(Math.Sqrt(Math.Pow(ay * Math.Cos(t12) - ax * Math.Sin(t12), 2) +
Math.Pow(m5_3 * Math.Cos(t33) + n5_3 * Math.Sin(t33), 2)),
(m5_3 * Math.Sin(t33) - n5_3 * Math.Cos(t33)) / (Math.Sin(f3) * Math.Sin(f4)));
double t56 = Math.Atan2(-Math.Sqrt(Math.Pow(ay * Math.Cos(t12) - ax * Math.Sin(t12), 2) +
Math.Pow(m5_3 * Math.Cos(t33) + n5_3 * Math.Sin(t33), 2)),
(m5_3 * Math.Sin(t33) - n5_3 * Math.Cos(t33)) / (Math.Sin(f3) * Math.Sin(f4)));
double t57 = Math.Atan2(Math.Sqrt(Math.Pow(ay * Math.Cos(t12) - ax * Math.Sin(t12), 2) +
Math.Pow(m5_4 * Math.Cos(t34) + n5_4 * Math.Sin(t34), 2)),
(m5_4 * Math.Sin(t34) - n5_4 * Math.Cos(t34)) / (Math.Sin(f3) * Math.Sin(f4)));
double t58 = Math.Atan2(-Math.Sqrt(Math.Pow(ay * Math.Cos(t12) - ax * Math.Sin(t12), 2) +
Math.Pow(m5_4 * Math.Cos(t34) + n5_4 * Math.Sin(t34), 2)),
(m5_4 * Math.Sin(t34) - n5_4 * Math.Cos(t34)) / (Math.Sin(f3) * Math.Sin(f4)));
// Calculate theta4 solutions
double t41 = (Math.Sin(t51) == 0) ? 0 : Math.Atan2(
((ay * Math.Cos(t11) - ax * Math.Sin(t11)) * Math.Sin(f1) * Math.Sin(f5)) / (-Math.Sin(t51) * Math.Sin(f3)),
(-m5_1 * Math.Cos(t31) - n5_1 * Math.Sin(t31)) / Math.Sin(t51));
double t42 = (Math.Sin(t52) == 0) ? 0 : Math.Atan2(
((ay * Math.Cos(t11) - ax * Math.Sin(t11)) * Math.Sin(f1) * Math.Sin(f5)) / (-Math.Sin(t52) * Math.Sin(f3)),
(-m5_1 * Math.Cos(t31) - n5_1 * Math.Sin(t31)) / Math.Sin(t52));
double t43 = (Math.Sin(t53) == 0) ? 0 : Math.Atan2(
((ay * Math.Cos(t11) - ax * Math.Sin(t11)) * Math.Sin(f1) * Math.Sin(f5)) / (-Math.Sin(t53) * Math.Sin(f3)),
(-m5_2 * Math.Cos(t32) - n5_2 * Math.Sin(t32)) / Math.Sin(t53));
double t44 = (Math.Sin(t54) == 0) ? 0 : Math.Atan2(
((ay * Math.Cos(t11) - ax * Math.Sin(t11)) * Math.Sin(f1) * Math.Sin(f5)) / (-Math.Sin(t54) * Math.Sin(f3)),
(-m5_2 * Math.Cos(t32) - n5_2 * Math.Sin(t32)) / Math.Sin(t54));
double t45 = (Math.Sin(t55) == 0) ? 0 : Math.Atan2(
((ay * Math.Cos(t12) - ax * Math.Sin(t12)) * Math.Sin(f1) * Math.Sin(f5)) / (-Math.Sin(t55) * Math.Sin(f3)),
(-m5_3 * Math.Cos(t33) - n5_3 * Math.Sin(t33)) / Math.Sin(t55));
double t46 = (Math.Sin(t56) == 0) ? 0 : Math.Atan2(
((ay * Math.Cos(t12) - ax * Math.Sin(t12)) * Math.Sin(f1) * Math.Sin(f5)) / (-Math.Sin(t56) * Math.Sin(f3)),
(-m5_3 * Math.Cos(t33) - n5_3 * Math.Sin(t33)) / Math.Sin(t56));
double t47 = (Math.Sin(t57) == 0) ? 0 : Math.Atan2(
((ay * Math.Cos(t12) - ax * Math.Sin(t12)) * Math.Sin(f1) * Math.Sin(f5)) / (-Math.Sin(t57) * Math.Sin(f3)),
(-m5_4 * Math.Cos(t34) - n5_4 * Math.Sin(t34)) / Math.Sin(t57));
double t48 = (Math.Sin(t58) == 0) ? 0 : Math.Atan2(
((ay * Math.Cos(t12) - ax * Math.Sin(t12)) * Math.Sin(f1) * Math.Sin(f5)) / (-Math.Sin(t58) * Math.Sin(f3)),
(-m5_4 * Math.Cos(t34) - n5_4 * Math.Sin(t34)) / Math.Sin(t58));
// Calculate theta6 solutions
double e1 = nx * Math.Sin(t11) - ny * Math.Cos(t11);
double f1_val = ox * Math.Sin(t11) - oy * Math.Cos(t11);
double t61 = Math.Atan2(
Math.Cos(t41) * e1 - Math.Cos(t51) * Math.Sin(t41) * f1_val,
Math.Cos(t41) * f1_val + Math.Cos(t51) * Math.Sin(t41) * e1);
double t62 = Math.Atan2(
Math.Cos(t42) * e1 - Math.Cos(t52) * Math.Sin(t42) * f1_val,
Math.Cos(t42) * f1_val + Math.Cos(t52) * Math.Sin(t42) * e1);
double t63 = Math.Atan2(
Math.Cos(t43) * e1 - Math.Cos(t53) * Math.Sin(t43) * f1_val,
Math.Cos(t43) * f1_val + Math.Cos(t53) * Math.Sin(t43) * e1);
double t64 = Math.Atan2(
Math.Cos(t44) * e1 - Math.Cos(t54) * Math.Sin(t44) * f1_val,
Math.Cos(t44) * f1_val + Math.Cos(t54) * Math.Sin(t44) * e1);
double e2 = nx * Math.Sin(t12) - ny * Math.Cos(t12);
double f2_val = ox * Math.Sin(t12) - oy * Math.Cos(t12);
double t65 = Math.Atan2(
Math.Cos(t45) * e2 - Math.Cos(t55) * Math.Sin(t45) * f2_val,
Math.Cos(t45) * f2_val + Math.Cos(t55) * Math.Sin(t45) * e2);
double t66 = Math.Atan2(
Math.Cos(t46) * e2 - Math.Cos(t56) * Math.Sin(t46) * f2_val,
Math.Cos(t46) * f2_val + Math.Cos(t56) * Math.Sin(t46) * e2);
double t67 = Math.Atan2(
Math.Cos(t47) * e2 - Math.Cos(t57) * Math.Sin(t47) * f2_val,
Math.Cos(t47) * f2_val + Math.Cos(t57) * Math.Sin(t47) * e2);
double t68 = Math.Atan2(
Math.Cos(t48) * e2 - Math.Cos(t58) * Math.Sin(t48) * f2_val,
Math.Cos(t48) * f2_val + Math.Cos(t58) * Math.Sin(t48) * e2);
// Combine all solutions into a 8x6 matrix
double[,] ikine_t = new double[8, 6]
{
{t11, t21, t31, t41, t51, t61},
{t11, t21, t31, t42, t52, t62},
{t11, t22, t32, t43, t53, t63},
{t11, t22, t32, t44, t54, t64},
{t12, t23, t33, t45, t55, t65},
{t12, t23, t33, t46, t56, t66},
{t12, t24, t34, t47, t57, t67},
{t12, t24, t34, t48, t58, t68}
};
return ikine_t;
}(4)UI中应用
正解
/// <summary>
/// 正解计算
/// </summary>
/// <param name="jointAngles"></param>
void RunDemoFK(double[] jointAngles)
{
//for (int i = 0; i < jointAngles.Length;i++ )
//{
// jointAngles[i] = jointAngles[i] * Math.PI / 180.0f;
//}
bDataModel = false;
try
{
var fk = new Puma560FK(MDH);
double[] jointAnglesTemp = new double[6];
for (int i = 0; i < jointAnglesTemp.Length; i++)
{
jointAnglesTemp[i] = jointAngles[i] ;
}
// 计算正运动学
double[,] T06 = fk.ForwardKinematics(jointAnglesTemp);
// 打印变换矩阵
for (int i = 0; i < 4; i++)
{
for (int j = 0; j < 4; j++)
{
//Console.Write(string.Format("{0,12:F6}", T06[i, j]));
}
}
txtMatrixFK_1_1.Text = T06[0, 0].ToString("f2");
txtMatrixFK_1_2.Text = T06[0, 1].ToString("f2");
txtMatrixFK_1_3.Text = T06[0, 2].ToString("f2");
txtMatrixFK_1_4.Text = T06[0, 3].ToString("f2");
txtMatrixFK_2_1.Text = T06[1, 0].ToString("f2");
txtMatrixFK_2_2.Text = T06[1, 1].ToString("f2");
txtMatrixFK_2_3.Text = T06[1, 2].ToString("f2");
txtMatrixFK_2_4.Text = T06[1, 3].ToString("f2");
txtMatrixFK_3_1.Text = T06[2, 0].ToString("f2");
txtMatrixFK_3_2.Text = T06[2, 1].ToString("f2");
txtMatrixFK_3_3.Text = T06[2, 2].ToString("f2");
txtMatrixFK_3_4.Text = T06[2, 3].ToString("f2");
txtMatrixFK_4_1.Text = T06[3, 0].ToString("f2");
txtMatrixFK_4_2.Text = T06[3, 1].ToString("f2");
txtMatrixFK_4_3.Text = T06[3, 2].ToString("f2");
txtMatrixFK_4_4.Text = T06[3, 3].ToString("f2");
// 打印末关节位置
double[] position = fk.GetPosition(T06);
txtPostionAbsX_FK.Text = position[0].ToString("f4");
txtPostionAbsY_FK.Text = position[1].ToString("f4");
txtPostionAbsZ_FK.Text = position[2].ToString("f4");
// 打印末关节欧拉角
double[] euler = fk.GetEulerAngles(T06);
//转换为角度
double[] eulerDeg = new double[3];
for (int i = 0; i < 3; i++)
{
eulerDeg[i] = euler[i] * 180 / Math.PI;
}
txtPostionAbsA_FK.Text = eulerDeg[0].ToString("f4"); //Roll
txtPostionAbsB_FK.Text = eulerDeg[1].ToString("f4"); //Pitch
txtPostionAbsC_FK.Text = eulerDeg[2].ToString("f4"); //Yaw
}
catch (Exception ex)
{
MessageBox.Show("Error: " + ex.Message);
}
txtJoinActualTheta1.Text = jointAngles[0].ToString("f4");
txtJoinActualTheta2.Text = jointAngles[1].ToString("f4");
txtJoinActualTheta3.Text = jointAngles[2].ToString("f4");
txtJoinActualTheta4.Text = jointAngles[3].ToString("f4");
txtJoinActualTheta5.Text = jointAngles[4].ToString("f4");
txtJoinActualTheta6.Text = jointAngles[5].ToString("f4");
//逆解
txtPostionAbsX_IK.Text = txtPostionAbsX_FK.Text;
txtPostionAbsY_IK.Text = txtPostionAbsY_FK.Text;
txtPostionAbsZ_IK.Text = txtPostionAbsZ_FK.Text;
txtPostionAbsA_IK.Text = txtPostionAbsA_FK.Text;
txtPostionAbsB_IK.Text = txtPostionAbsB_FK.Text;
txtPostionAbsC_IK.Text = txtPostionAbsC_FK.Text;
x = Convert.ToDouble(txtPostionAbsX_IK.Text);
y = Convert.ToDouble(txtPostionAbsY_IK.Text);
z = Convert.ToDouble(txtPostionAbsZ_IK.Text);
A = Convert.ToDouble(txtPostionAbsA_IK.Text);
B = Convert.ToDouble(txtPostionAbsB_IK.Text);
C = Convert.ToDouble(txtPostionAbsC_IK.Text);
RunDemoIK();
}逆解
void RunDemoIK()
{
bDataModel = true;
txtPostionAbsX_IK.Text = x.ToString("f4");
txtPostionAbsY_IK.Text = y.ToString("f4");
txtPostionAbsZ_IK.Text = z.ToString("f4");
txtPostionAbsA_IK.Text = A.ToString("f4");
txtPostionAbsB_IK.Text = B.ToString("f4");
txtPostionAbsC_IK.Text = C.ToString("f4");
try
{
Puma560IK solver = new Puma560IK(MDH);
// 测试用例1:标准位置
double[,] testPose1 = Puma560IK.CreateTransformMatrix(x, y, z, A, B, C);
Double[,] Solves_IK = solver.ComputeIK(testPose1); //角度值
//转换为角度值
for (int i = 0; i < Solves_IK.GetLength(0); i++)
{
for (int j = 0; j < Solves_IK.GetLength(1); j++)
{
Solves_IK[i, j] = Solves_IK[i, j] * 180 / Math.PI;
if(double.IsNaN(Solves_IK[i, j]))
{
throw new Exception("当前逆解计算不存在解!!!");
}
}
}
//第一组解
txtSolveIK_1_1.Text = Solves_IK[0, 0].ToString("f2");
txtSolveIK_1_2.Text = Solves_IK[0, 1].ToString("f2");
txtSolveIK_1_3.Text = Solves_IK[0, 2].ToString("f2");
txtSolveIK_1_4.Text = Solves_IK[0, 3].ToString("f2");
txtSolveIK_1_5.Text = Solves_IK[0, 4].ToString("f2");
txtSolveIK_1_6.Text = Solves_IK[0, 5].ToString("f2");
//第二组解
txtSolveIK_2_1.Text = Solves_IK[1, 0].ToString("f2");
txtSolveIK_2_2.Text = Solves_IK[1, 1].ToString("f2");
txtSolveIK_2_3.Text = Solves_IK[1, 2].ToString("f2");
txtSolveIK_2_4.Text = Solves_IK[1, 3].ToString("f2");
txtSolveIK_2_5.Text = Solves_IK[1, 4].ToString("f2");
txtSolveIK_2_6.Text = Solves_IK[1, 5].ToString("f2");
//第三组解
txtSolveIK_3_1.Text = Solves_IK[2, 0].ToString("f2");
txtSolveIK_3_2.Text = Solves_IK[2, 1].ToString("f2");
txtSolveIK_3_3.Text = Solves_IK[2, 2].ToString("f2");
txtSolveIK_3_4.Text = Solves_IK[2, 3].ToString("f2");
txtSolveIK_3_5.Text = Solves_IK[2, 4].ToString("f2");
txtSolveIK_3_6.Text = Solves_IK[2, 5].ToString("f2");
//第四组解
txtSolveIK_4_1.Text = Solves_IK[3, 0].ToString("f2");
txtSolveIK_4_2.Text = Solves_IK[3, 1].ToString("f2");
txtSolveIK_4_3.Text = Solves_IK[3, 2].ToString("f2");
txtSolveIK_4_4.Text = Solves_IK[3, 3].ToString("f2");
txtSolveIK_4_5.Text = Solves_IK[3, 4].ToString("f2");
txtSolveIK_4_6.Text = Solves_IK[3, 5].ToString("f2");
//第五组解
txtSolveIK_5_1.Text = Solves_IK[4, 0].ToString("f2");
txtSolveIK_5_2.Text = Solves_IK[4, 1].ToString("f2");
txtSolveIK_5_3.Text = Solves_IK[4, 2].ToString("f2");
txtSolveIK_5_4.Text = Solves_IK[4, 3].ToString("f2");
txtSolveIK_5_5.Text = Solves_IK[4, 4].ToString("f2");
txtSolveIK_5_6.Text = Solves_IK[4, 5].ToString("f2");
//第六组解
txtSolveIK_6_1.Text = Solves_IK[5, 0].ToString("f2");
txtSolveIK_6_2.Text = Solves_IK[5, 1].ToString("f2");
txtSolveIK_6_3.Text = Solves_IK[5, 2].ToString("f2");
txtSolveIK_6_4.Text = Solves_IK[5, 3].ToString("f2");
txtSolveIK_6_5.Text = Solves_IK[5, 4].ToString("f2");
txtSolveIK_6_6.Text = Solves_IK[5, 5].ToString("f2");
//第七组解
txtSolveIK_7_1.Text = Solves_IK[6, 0].ToString("f2");
txtSolveIK_7_2.Text = Solves_IK[6, 1].ToString("f2");
txtSolveIK_7_3.Text = Solves_IK[6, 2].ToString("f2");
txtSolveIK_7_4.Text = Solves_IK[6, 3].ToString("f2");
txtSolveIK_7_5.Text = Solves_IK[6, 4].ToString("f2");
txtSolveIK_7_6.Text = Solves_IK[6, 5].ToString("f2");
//第八组解
txtSolveIK_8_1.Text = Solves_IK[7, 0].ToString("f2");
txtSolveIK_8_2.Text = Solves_IK[7, 1].ToString("f2");
txtSolveIK_8_3.Text = Solves_IK[7, 2].ToString("f2");
txtSolveIK_8_4.Text = Solves_IK[7, 3].ToString("f2");
txtSolveIK_8_5.Text = Solves_IK[7, 4].ToString("f2");
txtSolveIK_8_6.Text = Solves_IK[7, 5].ToString("f2");
}
catch (Exception ex)
{
MessageBox.Show("Error: " + ex.Message);
}
}三、工程下载链接
https://download.csdn.net/download/panjinliang066333/92233890