基于方向谱与雷达信号处理的海杂波机理解析

前言

海杂波（sea clutter）指雷达在海面掠射或俯视条件下接收到的由海浪/涌浪产生的强散射回波。它不仅决定了海上探测的可探测性、虚警概率与恒虚警算法（CFAR）的门限设置，也直接影响弱小目标（小艇、海面低慢小无人机的海面散射分量、海鸟等）的检测性能。

1 海面起伏与方向谱建模

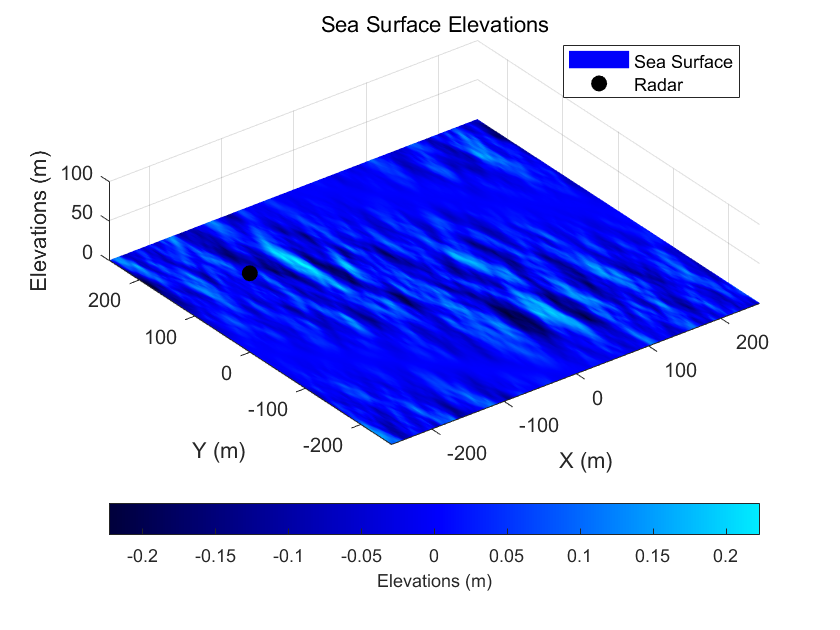
1.1 海面高度场的随机叠加模型

在频域合成思想下，海面高度场 z(x,y,t)z(x,y,t)z(x,y,t) 可表示为各个空间波数分量的叠加：
z(x,y,t)=∑kx,ky2,Φ(kx,ky)ΔkxΔkycos⁡(k⋅r−ω(∣∣k∣∣)t+φk). z(x,y,t)=\sum_{k_x,k_y}\sqrt{2,\Phi(k_x,k_y)\Delta k_x\Delta k_y} \cos\big(\mathbf{k}\cdot\mathbf{r}-\omega(||\mathbf{k}||)t+\varphi_{\mathbf{k}}\big). z(x,y,t)=kx,ky∑2,Φ(kx,ky)ΔkxΔky cos(k⋅r−ω(∣∣k∣∣)t+φk).

x,yx,yx,y：水平坐标（m）。
ttt：时间（s）。
r=[x,y]T\mathbf{r}=[x,y]^{\mathrm T}r=[x,y]T：位置向量。
k=[kx,ky]T\mathbf{k}=[k_x,k_y]^{\mathrm T}k=[kx,ky]T，∣k∣=K=kx2+ky2|\mathbf{k}|=K=\sqrt{k_x^2+k_y^2}∣k∣=K=kx2+ky2 ：二维波数与其模长（rad/m）。
Φ(kx,ky)\Phi(k_x,k_y)Φ(kx,ky)：二维方向谱 （单位：m3/rad2m^3/rad^2m3/rad2），刻画各波数方向上的能量分布。
Δkx,Δky\Delta k_x,\Delta k_yΔkx,Δky：波数格点间隔（rad/m）。
ω(K)\omega(K)ω(K)：角频率（rad/s），由色散关系确定。
φk\varphi_{\mathbf{k}}φk：随机相位，均匀分布于 [0,2π)[0,2\pi)[0,2π)。

该模型保证在适当的谱与色散关系下，海面是 平稳、各向不均匀（随风向） 的随机过程。

1.2 重力---毛细波色散关系

深水条件下，重力---毛细波的角频率与波数满足
ω(K)=gK+γK3. \omega(K)=\sqrt{gK+\gamma K^3}. ω(K)=gK+γK3 .

ggg：重力加速度m/s2m/s^2m/s2，通常取 (9.81)。
γ=σ/ρ\gamma=\sigma/\rhoγ=σ/ρ：毛细项系数m3/s2m^3/s^2m3/s2，σ\sigmaσ 为水的表面张力N/mN/mN/m，ρ\rhoρ 为水密度kg/m3kg/m^3kg/m3。
KKK：波数模长（rad/m）。

式中前项gKgKgK 主导长波（重力波），后项 γK3\gamma K^3γK3 主导短波（毛细波）。

1.3 方向谱：Phillips 型与方向展布

为简洁起见，常用经验证有效的 Phillips 型基谱并叠加方向展布与高波数衰减：
Φ(kx,ky)=S0(K)D(θ)T(K), \Phi(k_x,k_y)=S_0(K)D(\theta)T(K), Φ(kx,ky)=S0(K)D(θ)T(K),

其中
S0(K)=Aexp⁡(−1K2L2)K4,D(θ)=cos⁡sθI(cos⁡θ≥0),T(K)=exp⁡(−(KKh)2). S_0(K)=A\frac{\exp\big(-\tfrac{1}{K^2L^2}\big)}{K^4},\quad D(\theta)=\cos^s\theta\mathbb{I}({\cos\theta\ge 0}),\quad T(K)=\exp\big(-(\tfrac{K}{K_h})^2\big). S0(K)=AK4exp(−K2L21),D(θ)=cossθI(cosθ≥0),T(K)=exp(−(KhK)2).

AAA：谱强度常数（与风速/海况相关）。
LLL：与10 m高度风速 U10U_{10}U10 相关的尺度（m），经验地 L∼U102/gL\sim U_{10}^2/gL∼U102/g。
KhK_hKh：高波数截断（rad/m），抑制过多的短波能量。
θ\thetaθ：波数方向与风向夹角（rad）。
sss：方向展布指数（无量纲），风速越大，取值可越大（指向性越强）。
I⋅\mathbb{I}{\cdot}I⋅：指示函数，限定顺风半空间（避免与风向相反的波）。

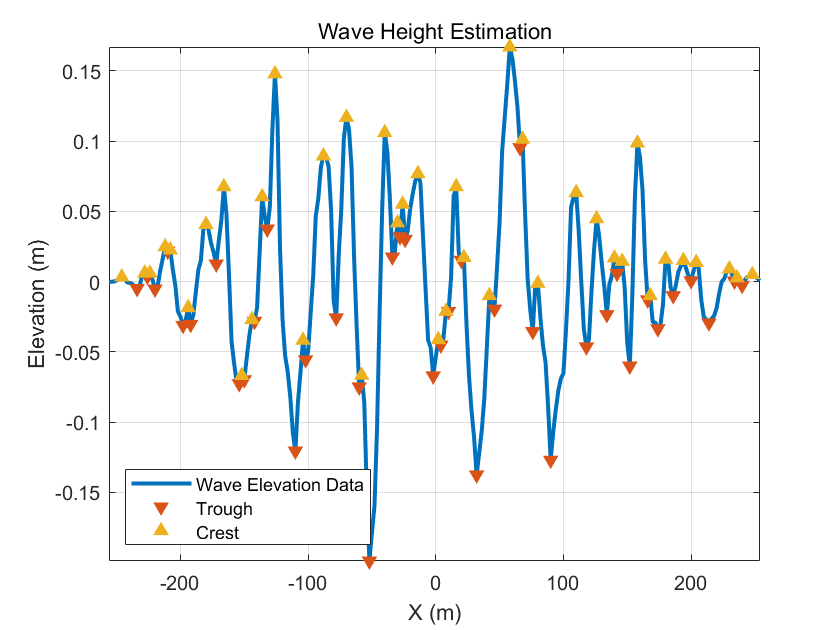
1.4 显著波高与谱矩

显著波高（Significant Wave Height, SWH）在谱表示中常近似为
Hs≈4m0,m0=∬Φ(kx,ky)dkxdky, H_s \approx 4\sqrt{m_0},\qquad m_0=\iint \Phi(k_x,k_y)\mathrm{d}k_x\mathrm{d}k_y, Hs≈4m0 ,m0=∬Φ(kx,ky)dkxdky,

HsH_sHs：显著波高mmm。
m0m_0m0：零阶谱矩m2m^2m2。

该式将方向谱能量与"宏观海况强度"建立联系。

2 雷达---海面几何与回波形成

2.1 俯视几何与主瓣脚印

雷达高度为 (h)，俯仰俯角为 (\psi)（相对水平面向下为正），主瓣方位 3 dB 波束宽度为 (\beta)。则波束中心斜距 近似
R0=hsin⁡ψ, R_0=\frac{h}{\sin\psi}, R0=sinψh,

R0R_0R0：波束中心到海面交会处的斜距（m）。
hhh：雷达高程（m）。
ψ\psiψ：俯角（rad）。

主瓣在该斜距处的横向（方位）宽度近似
Waz≈R0tan⁡β2. W_{\text{az}}\approx R_0 \tan\frac{\beta}{2}. Waz≈R0tan2β.

WazW_{\text{az}}Waz：主瓣横向 3 dB 宽度（m）。
β\betaβ：方位波束宽度（rad）。

2.2 雷达方程与散射单元

将海面离散为面积 ΔA\Delta AΔA 的小面元，采用等效雷达散射截面密度 （NRCS）σ0\sigma_0σ0 模型，则第 kkk 个面元对接收端的复包络贡献可写为
ak=σ0ΔARk2ejϕk,τk=2Rkc. a_k=\frac{\sqrt{\sigma_0\Delta A}}{R_k^{2}}e^{j\phi_k}, \qquad \tau_k=\frac{2R_k}{c}. ak=Rk2σ0ΔA ejϕk,τk=c2Rk.

aka_kak：第 kkk 面元的复散射幅度（线性幅值）。
σ0\sigma_0σ0：NRCS（无量纲，线性域）。
ΔA\Delta AΔA：面元面积m2m^2m2。
RkR_kRk：雷达到该面元的斜距mmm。
ϕk\phi_kϕk：随机相位radradrad。
τk\tau_kτk：往返传播时延sss。
ccc：光速m/sm/sm/s。

总回波（基带） 是所有面元经传播时延后的叠加：
r(t)=∑kakstx(t−τk), r(t)=\sum_k a_ks_{\text{tx}}(t-\tau_k), r(t)=k∑akstx(t−τk),

r(t)r(t)r(t)：接收端基带回波（复包络）。
stx(t)s_{\text{tx}}(t)stx(t)：发射基带脉冲（复包络）。

2.3 线性调频脉冲与匹配滤波

发射端常用线性调频（LFM）脉冲
stx(t)=exp⁡(jπμ(t−T2)2)I(0≤t<T), s_{\text{tx}}(t)=\exp\big(j\pi\mu (t-\tfrac{T}{2})^2\big)\mathbb{I}({0\le t<T}), stx(t)=exp(jπμ(t−2T)2)I(0≤t<T),

TTT：脉冲宽度（s）。
BBB：调频带宽（Hz）。
μ=B/T\mu=B/Tμ=B/T：调频率（Hz/s）。
I(⋅)\mathbb{I}({\cdot})I(⋅)：脉冲门限函数。

其匹配滤波输出
y(τ)=∫r(t)stx∗(t−τ)dt, y(\tau)=\int r(t)s_{\text{tx}}^*(t-\tau)\mathrm{d}t, y(τ)=∫r(t)stx∗(t−τ)dt,

y(τ)y(\tau)y(τ)：匹配滤波输出（复包络，延时 τ\tauτ 的函数）。
(⋅)∗(\cdot)^*(⋅)∗：复共轭。

匹配滤波后，距离分辨率近似为
ΔR=c2B. \Delta R=\frac{c}{2B}. ΔR=2Bc.

ΔR\Delta RΔR：距离向分辨率（m）。
BBB：带宽（Hz）。

3 海杂波的多普勒与时频表征

3.1 面元径向速度与多普勒

海面在重力---毛细波作用下产生轨道运动。每个散射面元的径向速度 vr,kv_{r,k}vr,k 使回波产生多普勒频移
fd,k=2vr,kλ, f_{d,k}=\frac{2 v_{r,k}}{\lambda}, fd,k=λ2vr,k,

fd,kf_{d,k}fd,k：第 kkk 面元的多普勒（Hz）。
vr,kv_{r,k}vr,k：径向速度（m/s）。
λ=c/fc\lambda=c/f_cλ=c/fc：波长(m)，fcf_cfc 为载频（Hz）。

反之，常把频率映射为速度
v=λ2fd. v=\frac{\lambda}{2}f_d . v=2λfd.

vvv：等效径向速度m/sm/sm/s。
fdf_dfd：多普勒频率HzHzHz。

3.2 短时傅里叶变换（STFT）

序列 x[n]x[n]x[n] 的 STFT 定义为
X(m,n)=∑p=0L−1x[n+p]w[p]e−j2πmp/L, X(m,n)=\sum_{p=0}^{L-1} x[n+p]w[p] e^{-j2\pi m p/L}, X(m,n)=p=0∑L−1x[n+p]w[p]e−j2πmp/L,

X(m,n)X(m,n)X(m,n)：第 nnn 个时间窗、第 mmm 个频率格点的 STFT 系数（复数）。
w[p]w[p]w[p]：长度为 LLL 的窗函数（如汉宁窗），0≤p<L0\le p<L0≤p<L。
LLL：窗长（点数）。
nnn：时间索引（以"跳步" HHH 递增，HHH 为步进）。
mmm：频率索引(0≤m<L−1)(0\le m<L-1)(0≤m<L−1)。

对匹配滤波输出某一距离单元随脉冲序号的序列做 STFT，可得到速度---时间谱图 ，常用于观察海杂波的缓慢起伏 与随机快变。

4 海杂波幅度统计模型

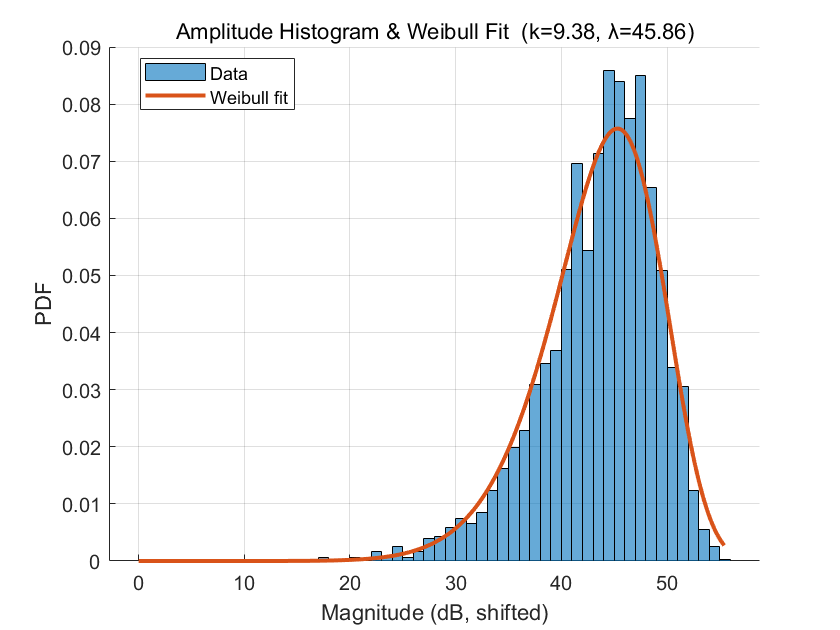
4.1 Weibull 分布（工程近似）

海杂波幅度（或强度）的边缘统计在中高分辨率下，常可用 Weibull 分布近似：
pA(a)=kλ(aλ)k−1exp⁡[−(aλ)k],a≥0. p_A(a)=\frac{k}{\lambda}\Big(\frac{a}{\lambda}\Big)^{k-1} \exp\Big[-\Big(\frac{a}{\lambda}\Big)^{k}\Big],\quad a\ge 0 . pA(a)=λk(λa)k−1exp[−(λa)k],a≥0.

pA(a)p_A(a)pA(a)：幅度随机变量 AAA 的概率密度函数（1/幅度单位）。
k>0k>0k>0：形状参数（无量纲），控制尾部厚度。
λ>0\lambda>0λ>0：尺度参数（与均值/方差有关）。
aaa：幅度取值（线性域）。

对数域（dB）展示时，经
AdB=20log⁡10A A_{\mathrm{dB}}=20\log_{10} A AdB=20log10A

AdBA_{\mathrm{dB}}AdB：幅度的 dB 值（dB）。
AAA：线性幅度（同上）。

4.2 其它常见模型（简述）

K 分布 ：当回波为散斑_目标强度_慢变的乘性模型时适用，重尾更显著。
对数正态：在若干叠加与乘性效应下的经验近似。
复高斯：当散射面元数目很大且相位均匀、满足中心极限定理时，复包络趋于高斯。

不同雷达配置与海况下，经验上 Weibull/K/对数正态会呈现不同的拟合优劣，需要基于实测或高保真仿真进行模型选择与参数估计。

个人开源代码链接：https://github.com/hjHe-ee/Sea-clutter-simulation

总结

本文以"移动海面回波仿真"的典型处理链为参考，从方向谱建模 、重力---毛细波色散 、雷达---海面几何与回波形成 、匹配滤波与时频分析 到海杂波统计建模系统梳理了海杂波的关键机理。