一、Binary Classification(二元分类)
1.1 什么是二元分类?
二元分类是机器学习中一种分类任务,目标是将样本分为两个互斥的类别。
- 典型问题示例:
- 邮件是否为垃圾邮件?答案(标签y)只有 "no(不是)" 或 "yes(是)"。
- 交易是否欺诈?答案只有 "no(不是)" 或 "yes(是)"。
- 肿瘤是否恶性?答案只有 "no(不是)" 或 "yes(是)"。
- 标签的数值化:为了方便计算,通常把两个类别映射为0 和 1(比如 "no/false" 对应 0,"yes/true" 对应 1)。
1.2 如何用模型做二元分类?
我们可以用线性模型 fw,b(x)=wx+b(类似一次函数 y=kx+c)来预测,再通过阈值(Threshold)判断类别。
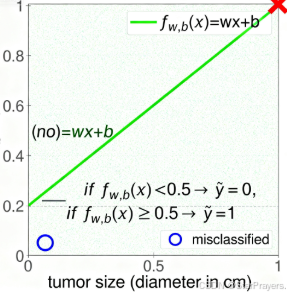
以 "肿瘤是否恶性" 为例,x 是肿瘤大小(直径,单位 cm),模型输出 fw,b(x),然后用0.5 作为阈值判断:
- 如果 fw,b(x)<0.5,预测 y^=0(肿瘤为良性,"no");
- 如果 fw,b(x)≥0.5,预测 y^=1(肿瘤为恶性,"yes")。
而 决策边界(Decision Boundary) 就是模型输出等于阈值的那条线。把输入空间分成两部分,分别对应两个类别。
"分类错误(misclassified)" 情况:有些实际为 1(恶性,红叉)的样本被分到了 0 的区域,或实际为 0(良性,蓝圈)的样本被分到了 1 的区域 ------ 这是模型需要优化的地方。
二、逻辑回归
2.1 逻辑回归的背景与需求
在分类问题中(比如判断肿瘤是否为恶性),我们需要模型的输出在 0 到 1 之间(表示 "属于某一类的概率")。
- 以 "肿瘤大小(x,单位 cm)判断是否恶性(y)" 为例:
- y=1 表示 "恶性(yes)",y=0 表示 "非恶性(no)"。
- 我们需要一个模型,输入 "肿瘤大小 x",输出一个0 到 1 之间的数值,用来表示 "该肿瘤是恶性的概率"。
2.2 Sigmoid 函数(逻辑函数)
为了让输出落在 0 到 1 之间,我们引入 sigmoid 函数,公式为:
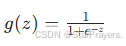
其中 z 是一个线性组合(后面会讲),g(z) 是 sigmoid 函数的输出。
2.3 Sigmoid 函数的形状与取值
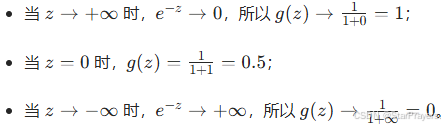
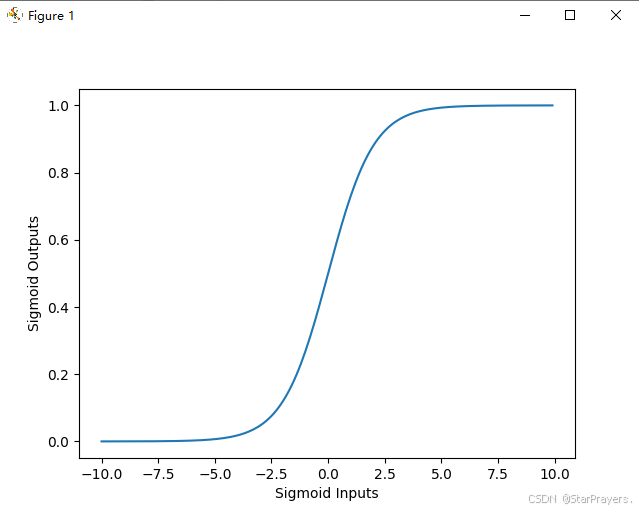
直观理解(结合图像)
右侧的 sigmoid 函数图像中,横轴是z,纵轴是g(z):
- 当z=100时,g(z)≈1;
- 当z=0时,g(z)=0.5;
- 当z=−100时,g(z)≈0。
2.4 逻辑回归模型:从输入到输出的过程
逻辑回归模型的核心是 **"线性组合 + sigmoid 函数"** 的组合,步骤如下:
1. 线性组合:
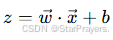
- x 是输入特征(比如 "肿瘤大小",如果是多特征还可以包含 "肿瘤密度" 等);
- w 是权重(每个特征对结果的 "重要程度");
- b 是偏置(相当于线性函数的截距,控制模型的基准输出);
- z 是线性组合的结果,它是一个实数(可以是正、负或 0)。
2. 代入 sigmoid 函数:得到逻辑回归的预测输出
将z=w⋅x+b代入 sigmoid 函数g(z),得到逻辑回归的模型:
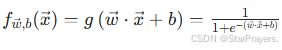
2.5 逻辑回归输出的解释
模型输出fw,b(x)的含义是 "给定输入x和参数w,b时,y=1 的概率",即:
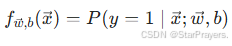
- 因为概率总和为 1,所以 P(y=0∣x;w,b)=1−P(y=1∣x;w,b);
- 举例:若fw,b(x)=0.7,则表示 "该肿瘤是恶性(y=1)的概率为 70%"。
2.6 总结
逻辑回归是一种分类算法,通过 "线性组合 + Sigmoid 函数" 的结构,让输出落在 0 到 1 之间,从而表示 "属于某一类的概率"。它的核心是 Sigmoid 函数的变形能力(把任意实数映射到 0-1 区间),以及对输出概率的可解释性(直接对应分类的置信度)。
三、**Decision Boundary(**决策边界)
要彻底理解决策边界(Decision Boundary)的概念,我们可以分线性决策边界 和非线性决策边界两个模块来拆解:
3.1 线性决策边界
逻辑回归中,当输入特征的组合是线性形式 时,决策边界是一条直线(二维场景)或平面(高维场景)。
1. 数学推导
逻辑回归的模型是 fw,b(x)=g(w⋅x+b),其中 g(z) 是 sigmoid 函数。
- 当 z=w⋅x+b=0 时,g(z)=0.5(sigmoid 函数在z=0时输出 0.5)。
- 我们将 z=0 作为决策边界的判定条件 :
- 若 z>0,则 g(z)>0.5,模型预测 y=1;
- 若 z<0,则 g(z)<0.5,模型预测 y=0。
2. 例子:二维线性决策边界
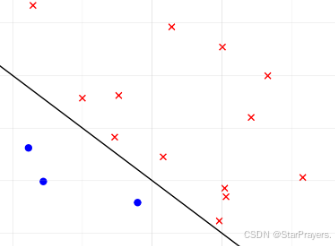
- 模型的线性组合为 z=x1+x2−3(即 w1=1,w2=1,b=−3);
- 决策边界为 z=0,即 x1+x2−3=0,化简得 x1+x2=3(一条直线)。
- 图像中:
- 直线上方的样本(红叉)满足 x1+x2>3,即 z>0,模型预测 y=1;
- 直线下方的样本(蓝圈)满足 x1+x2<3,即 z<0,模型预测 y=0。
3.2 非线性决策边界
现实中很多分类问题不是 "线性可分" 的(即无法用直线 / 平面分开两类样本),此时需要引入非线性特征组合 (如平方项、交叉项、高次项等),从而得到非线性的决策边界(曲线、椭圆、更复杂的形状)。
1. 例子:圆形决策边界
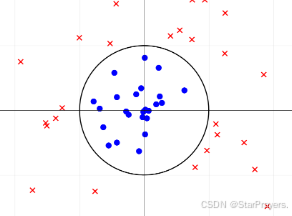
- 模型的线性组合包含特征的平方项:z=x12+x22−1(即 w1=1,w2=1,b=−1,这里的 "线性组合" 是对 "非线性特征(x12,x22)" 的线性加权);
- 决策边界为 z=0,即 x12+x22−1=0,化简得 x12+x22=1(一个以原点为圆心、半径为 1 的圆)。
- 图像中:
- 圆内的样本(蓝圈)满足 x12+x22<1,即 z<0,模型预测 y=0;
- 圆外的样本(红叉)满足 x12+x22>1,即 z>0,模型预测 y=1。
2. 更复杂的非线性决策边界
当引入更多非线性特征(如三次项 x13、交叉项 x1x2、二次项 x22 等)时,决策边界可以是椭圆 、不规则曲线等更复杂的形状。
-
模型的线性组合形式为:
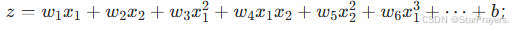
-
决策边界由 z=0 决定,形状由这些非线性特征的组合方式决定(比如含 x12 和 x22 且系数不同时,会形成椭圆)。
3.3 总结
决策边界是逻辑回归(或其他分类模型)用来区分不同类别样本的 "分界线":
- 当特征是线性组合时,决策边界是直线 / 平面(线性决策边界);
- 当引入非线性特征(如平方项、高次项、交叉项)时,决策边界可以是曲线、圆、椭圆等复杂形状(非线性决策边界)。