深度学习周报（10.27~11.2）

[1《Improving Language Understanding by Generative Pre-Training》代码](#1《Improving Language Understanding by Generative Pre-Training》代码)

[1.1 transformer 块](#1.1 transformer 块)

[1.2 训练器定义](#1.2 训练器定义)

[1.3 无监督预训练](#1.3 无监督预训练)

[1.4 有监督微调](#1.4 有监督微调)

[1.5 评估](#1.5 评估)

[2 量子相位估计](#2 量子相位估计)

[3 总结](#3 总结)

摘要

本周首先补充学习了上周论文的代码，了解了其一些具体实现细节，对 transformer 有了进一步的认识；其次学习了量子相位估计算法，了解了其电路结构与具体步骤，认识了相位反冲、本征向量、逆量子傅里叶变换等概念。

Abstract

This week, I first supplemented my learning of last week's paper by studying its code, gaining insights into some specific implementation details and deepening my understanding of the Transformer. Secondly, I learned about the quantum phase estimation algorithm, exploring its circuit structure and specific steps, and familiarizing myself with concepts such as phase kickback, eigenvectors, and the inverse quantum Fourier transform.

1 《Improving Language Understanding by Generative Pre-Training》代码

1.1 模型定义

文章训练了一个仅包含12层解码器的 transformer ， transformer 块的代码与前面梳理其架构类似，故代码在此不再赘述。最终封装了 LayerNorm（归一化层）、MultiHeadAttention（多头注意力）、PositionwiseFeedforward（位置前馈网络）与 TransformerBlock（transformer块）四个类。

与前面梳理架构时不同的地方主要有两个，一是给后三个类都加入了0.1的 dropout 以防止过拟合；二是在位置前馈网络里改用了 GELU激活函数，它结合了ReLU的整流特性与dropout的随机性训练过程更加稳定，性能也更好。

接着分别定义了用于无监督预训练和有监督微调的模型，之所以分别定义是由于两阶段的任务目标与输出结构均不同。前者是语言建模任务，输出为序列级，而后者是分类或者其他下游任务，输出通常为文档级，所以分开定义更加清晰，也更加符合模块化设计。

无监督预训练：

python 复制代码

# 无监督预训练模型
class GPT1(nn.Module):
    # 模型参数均来自论文
    def __init__(self, vocab_size, max_seq_length, hidden_size=768, num_layers=12,
                 num_heads=12, ff_size=3072, dropout=0.1):
        super(GPT1, self).__init__()

        # 初始化
        self.vocab_size = vocab_size
        self.max_seq_length = max_seq_length
        self.hidden_size = hidden_size
        self.num_layers = num_layers

        # 词嵌入和位置编码
        self.token_embedding = nn.Embedding(vocab_size, hidden_size)
        self.position_embedding = nn.Embedding(max_seq_length, hidden_size)

        # Transformer层：创建12个transformerBlock，前一个输出是后一个的输入
        self.layers = nn.ModuleList([
            TransformerBlock(hidden_size, num_heads, ff_size, dropout)
            for _ in range(num_layers)   #用下划线作为循环变量，表示只需重复执行循环体
        ])

        # 层归一化和输出层
        self.layer_norm = LayerNorm(hidden_size)
        self.lm_head = nn.Linear(hidden_size, vocab_size, bias=False)

        # 权重绑定（输出层和嵌入层共享权重，减少参数量，提升训练稳定性）
        self.lm_head.weight = self.token_embedding.weight

        self.dropout = nn.Dropout(dropout)

        # 初始化权重
        self.apply(self._init_weights)

    def _init_weights(self, module):
        # 线性层和嵌入层
        if isinstance(module, (nn.Linear, nn.Embedding)):
            module.weight.data.normal_(mean=0.0, std=0.02)
            if isinstance(module, nn.Linear) and module.bias is not None:
                module.bias.data.zero_()
        # 归一化层
        elif isinstance(module, LayerNorm):
            module.bias.data.zero_()
            module.weight.data.fill_(1.0)

    def forward(self, input_ids, attention_mask=None, labels=None):
        batch_size, seq_length = input_ids.shape

        # 创建位置索引
        position_ids = torch.arange(0, seq_length, dtype=torch.long, device=input_ids.device)
        position_ids = position_ids.unsqueeze(0).expand(batch_size, seq_length)

        # 获取嵌入
        token_embeddings = self.token_embedding(input_ids)
        position_embeddings = self.position_embedding(position_ids)

        # 组合嵌入
        x = self.dropout(token_embeddings + position_embeddings)

        # 创建因果mask（防止看到未来的token）
        mask = self._create_causal_mask(seq_length, input_ids.device)

        # 通过Transformer层
        for layer in self.layers:
            x = layer(x, mask)

        x = self.layer_norm(x)

        # 语言模型头
        logits = self.lm_head(x)

        # 计算损失（如果提供了labels）
        loss = None
        if labels is not None:
            # 语言建模任务：预测下一个token
            shift_logits = logits[..., :-1, :].contiguous()
            shift_labels = labels[..., 1:].contiguous()
            loss_fct = nn.CrossEntropyLoss()
            loss = loss_fct(shift_logits.view(-1, shift_logits.size(-1)),
                            shift_labels.view(-1))

        return {'logits': logits, 'loss': loss}
    
    # 创建因果mask
    def _create_causal_mask(self, seq_length, device):
        
        mask = torch.tril(torch.ones(seq_length, seq_length, device=device))
        mask = mask.unsqueeze(0).unsqueeze(1)  
        return mask

有监督微调：

python 复制代码

# 有监督微调模型（以分类任务为例）
class GPT1ForClassification(nn.Module):

    def __init__(self, gpt_model, num_classes, dropout=0.1):
        super(GPT1ForClassification, self).__init__()
        self.gpt = gpt_model
        self.classifier = nn.Linear(gpt_model.hidden_size, num_classes)
        self.dropout = nn.Dropout(dropout)

    def forward(self, input_ids, attention_mask=None, labels=None):
        # 通过GPT获取隐藏状态
        outputs = self.gpt(input_ids, attention_mask)
        hidden_states = outputs['logits']  # 实际上是最后一个隐藏层

        # 使用最后一个token的隐藏状态进行分类
        last_token_hidden = hidden_states[:, -1, :]
        pooled_output = self.dropout(last_token_hidden)
        logits = self.classifier(pooled_output)

        loss = None
        if labels is not None:
            loss_fct = nn.CrossEntropyLoss()
            loss = loss_fct(logits.view(-1, logits.size(-1)), labels.view(-1))

        return {'logits': logits, 'loss': loss}

1.2 训练器定义

python 复制代码

#  无监督预训练数据集
class UnsupervisedDataset(Dataset):
    def __init__(self, texts, tokenizer, max_length=512):
        self.texts = texts
        self.tokenizer = tokenizer
        self.max_length = max_length

    def __len__(self):
        return len(self.texts)

    def __getitem__(self, idx):
        text = self.texts[idx]

        # 分词
        encoding = self.tokenizer(
            text,
            max_length=self.max_length,
            padding='max_length',
            truncation=True,
            return_tensors='pt'
        )

        # 对于无监督预训练，输入和标签相同（但标签右移一位）
        input_ids = encoding['input_ids'].squeeze()

        return {
            'input_ids': input_ids,
            'labels': input_ids.clone()  # 语言建模任务
        }

# 有监督微调数据集（分类任务）
class SupervisedDataset(Dataset):
    def __init__(self, texts, labels, tokenizer, max_length=512):
        self.texts = texts
        self.labels = labels
        self.tokenizer = tokenizer
        self.max_length = max_length

    def __len__(self):
        return len(self.texts)

    def __getitem__(self, idx):
        text = self.texts[idx]
        label = self.labels[idx]

        encoding = self.tokenizer(
            text,
            max_length=self.max_length,
            padding='max_length',
            truncation=True,
            return_tensors='pt'
        )

        return {
            'input_ids': encoding['input_ids'].squeeze(),
            'labels': torch.tensor(label, dtype=torch.long)
        }

# 训练器定义
class GPT1Trainer:
    def __init__(self, model, model_type, learning_rate, warmup_steps=16000):
        self.model = model
        self.model_type = model_type  
        self.optimizer = torch.optim.AdamW(
            model.parameters(),
            lr=learning_rate,
            weight_decay=0.01
        )
        self.scheduler = torch.optim.lr_scheduler.LambdaLR(
            self.optimizer,
            lr_lambda=lambda step: min(1.0, step / warmup_steps)
        )

    def train_step(self, batch):
        self.model.train()
        self.optimizer.zero_grad()

        # 前向传播
        if self.model_type == "unsupervised":
            # 无监督预训练
            outputs = self.model(
                input_ids=batch['input_ids'],
                labels=batch['labels']
            )
        else:
            # 有监督微调
            outputs = self.model(
                input_ids=batch['input_ids'],
                labels=batch['labels']
            )

        loss = outputs['loss']
        loss.backward()

        # 梯度裁剪
        torch.nn.utils.clip_grad_norm_(self.model.parameters(), 1.0)

        self.optimizer.step()
        self.scheduler.step()

        return loss.item()

    def evaluate(self, dataloader):
        self.model.eval()
        total_loss = 0
        total_samples = 0

        with torch.no_grad():
            for batch in dataloader:
                if self.model_type == "unsupervised":
                    outputs = self.model(
                        input_ids=batch['input_ids'],
                        labels=batch['labels']
                    )
                else:
                    outputs = self.model(
                        input_ids=batch['input_ids'],
                        labels=batch['labels']
                    )

                total_loss += outputs['loss'].item() * len(batch['input_ids'])
                total_samples += len(batch['input_ids'])

        return total_loss / total_samples

    def save_model(self, path):
        torch.save({
            'model_state_dict': self.model.state_dict(),
            'optimizer_state_dict': self.optimizer.state_dict(),
        }, path)

    def load_model(self, path):
        checkpoint = torch.load(path)
        self.model.load_state_dict(checkpoint['model_state_dict'])
        self.optimizer.load_state_dict(checkpoint['optimizer_state_dict'])

1.3 无监督预训练

python 复制代码

# 无监督预训练阶段 
def unsupervised_pretraining():
   
    print("开始无监督预训练阶段")

    # 配置参数（基于GPT-1论文）
    config = {
        'vocab_size': 50257,  
        'max_seq_length': 512,
        'hidden_size': 768,
        'num_layers': 12,
        'num_heads': 12,
        'ff_size': 3072,
        'dropout': 0.1
    }

    # 创建模型
    model = GPT1(**config)

    # 创建训练器
    trainer = GPT1Trainer(model, model_type="unsupervised", learning_rate=6.25e-5)

    # 准备数据
    tokenizer = GPT2Tokenizer.from_pretrained('gpt2')
    tokenizer.pad_token = tokenizer.eos_token

    texts = prepare_unsupervised_data()
    dataset = UnsupervisedDataset(texts, tokenizer)
    dataloader = DataLoader(dataset, batch_size=4, shuffle=True)

    # 训练循环
    num_epochs = 3
    for epoch in range(num_epochs):
        total_loss = 0
        progress_bar = tqdm(dataloader, desc=f"Epoch {epoch + 1}/{num_epochs}")

        for i, batch in enumerate(progress_bar):
            loss = trainer.train_step(batch)
            total_loss += loss

            # 更新进度条
            progress_bar.set_postfix({"loss": f"{loss:.4f}"})

            # 每50个batch记录一次
            if i % 50 == 0:
                avg_loss = total_loss / (i + 1)
                print(f"Epoch {epoch + 1}, Batch {i}, Average Loss: {avg_loss:.4f}")

        # 计算平均损失
        avg_loss = total_loss / len(dataloader)
        print(f"无监督预训练 - Epoch {epoch + 1} 完成，平均损失: {avg_loss:.4f}")

        # 保存模型检查点
        trainer.save_model(f"gpt1_pretrained_epoch_{epoch + 1}.pt")

    print("无监督预训练完成！")
    return model

1.4 有监督微调

python 复制代码

# 有监督微调阶段 
def supervised_finetuning(pretrained_model):

    print("开始有监督微调阶段")

    # 创建分类模型
    num_classes = 2  # 二分类任务
    model = GPT1ForClassification(pretrained_model, num_classes)

    # 创建训练器（使用更小的学习率）
    trainer = GPT1Trainer(model, model_type="supervised", learning_rate=1e-5)

    # 准备数据
    tokenizer = GPT2Tokenizer.from_pretrained('gpt2')
    tokenizer.pad_token = tokenizer.eos_token

    texts, labels = prepare_supervised_data()
    dataset = SupervisedDataset(texts, labels, tokenizer)
    dataloader = DataLoader(dataset, batch_size=4, shuffle=True)

    # 训练循环
    num_epochs = 5
    best_accuracy = 0

    for epoch in range(num_epochs):
        total_loss = 0
        correct_predictions = 0
        total_predictions = 0

        progress_bar = tqdm(dataloader, desc=f"Epoch {epoch + 1}/{num_epochs}")

        for i, batch in enumerate(progress_bar):
            loss = trainer.train_step(batch)
            total_loss += loss

            # 计算准确率
            with torch.no_grad():
                outputs = model(input_ids=batch['input_ids'])
                predictions = torch.argmax(outputs['logits'], dim=-1)
                correct_predictions += (predictions == batch['labels']).sum().item()
                total_predictions += batch['labels'].size(0)

            accuracy = correct_predictions / total_predictions

            # 更新进度条
            progress_bar.set_postfix({
                "loss": f"{loss:.4f}",
                "accuracy": f"{accuracy:.4f}"
            })

        # 计算平均指标
        avg_loss = total_loss / len(dataloader)
        accuracy = correct_predictions / total_predictions

        print(f"有监督微调 - Epoch {epoch + 1} 完成")
        print(f"平均损失: {avg_loss:.4f}, 准确率: {accuracy:.4f}")

        # 保存最佳模型
        if accuracy > best_accuracy:
            best_accuracy = accuracy
            trainer.save_model("gpt1_finetuned_best.pt")
            print(f"新的最佳模型已保存，准确率: {accuracy:.4f}")

    print(f"有监督微调完成！最佳准确率: {best_accuracy:.4f}")
    return model

1.5 评估

python 复制代码

# 评估模型性能
def evaluate_model(model, test_texts, test_labels, tokenizer):

    print("模型评估")

    model.eval()
    correct_predictions = 0
    total_predictions = 0

    with torch.no_grad():
        for text, label in zip(test_texts, test_labels):
            encoding = tokenizer(
                text,
                max_length=512,
                padding='max_length',
                truncation=True,
                return_tensors='pt'
            )

            outputs = model(input_ids=encoding['input_ids'])
            prediction = torch.argmax(outputs['logits'], dim=-1).item()

            if prediction == label:
                correct_predictions += 1
            total_predictions += 1

    accuracy = correct_predictions / total_predictions
    print(f"测试准确率: {accuracy:.4f} ({correct_predictions}/{total_predictions})")

    return accuracy

2 量子相位估计

量子相位估计将不可测量的相位信息转换为可测量的振幅信息。

具体而言，它利用相位反冲（Phase Kickback）将酉操作 U 的相位写入计数寄存器 qubit ，再利用逆量子傅里叶变换将量子态从傅里叶基转换到计算基，从而进行测量。

其中 Phase Kickback 描述的是一种现象，即当一个控制量子比特和一个目标量子比特通过一个受控门发生相互作用时，目标量子比特的相位信息可以被"踢回"并编码到控制量子比特的状态中，这也意味着，目标量子比特会通过其相位反过来影响控制量子比特。

酉操作的相位指的是该操作的本征值的相位。在量子力学中，系统的演化由酉算子 U 来描述，满足，这意味着它是可逆的且保持概率总和为1。对于任何算子，都存在一些特殊的向量（），当该算子作用于它们时，只会使向量伸长或旋转，而不会改变其方向，用数学公式表达就是：

这些向量被称为本征向量，其中被称为本征值，是一个复数。

由于 U 是酉算子，它有一个非常重要的性质，即它的所有本征值的模都是 1。而任何模为1的复数都可以写成的形式，其中的就是相位，它是一个实数。对于一个酉操作 U ，其相位就是它的本征值在复平面单位圆上所对应的角度，为了数学上的便利和算法的自然表达，通常会将本征值表示为，用来表示我们想要估计的相位。

逆量子傅里叶变换（IQFT）从字面上就很好理解，就是量子傅里叶变换（QFT）的逆运算，它将频域表示转换回时域信号，将傅里叶基态转换为计算基态，从包含相位信息的量子态中，"读取"或"解码"出我们想要的经典信息，其公式如下：

在完成逆量子傅里叶变换之后，计数寄存器的状态会变为：

其中是一个确定的二进制字符串，代表了对相位的估计值。此时在计算基下对计数寄存器中的每一个量子比特进行单独的测量，每个量子比特都会坍缩到与上。

p.s. 在完成逆量子傅里叶变换之后，如果相位可以被精确表示，量子态就是一个确定的基态；如果相位不能被精确表示，则是一个以高概率集中于某个基态的叠加态。而坍缩这种现象的发生并不与叠加态绑定。

最终得到的二进制字符串对应的十进制数值表示就是对相位的估计。

相位估计的过程涉及两组量子寄存器，计数寄存器与目标寄存器，前者包含 t 个初始化为的量子比特，而后者初始化为 U 的特征态。其电路结构如下所示：

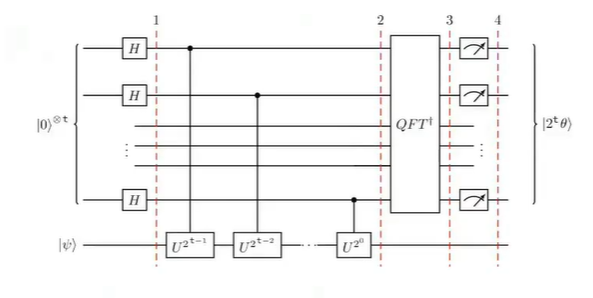
（图中以及前面公式中的 t 相当于前面学习时的 n，即量子比特数）

整个算法分为如下几个主要步骤：

首先，制备叠加态，即对计数寄存器中的每一个量子比特施加一个 H 门，此后整个系统的状态会变为：

其次，执行受控酉算子，这也是算法的核心。具体是对计数寄存器的第 j 个量子比特，执行一个受控的操作。这个阶段会发生相位反冲，目标寄存器始终保持不变，相位信息通过受控操作踢回到计数寄存器。计数寄存器的状态现在是一个包含了相位信息的傅里叶态，但被编码在基态的振幅中，我们无法直接测量读取。假设：

那么，此后整个系统的状态会变为

然后，对计数寄存器执行逆量子傅里叶变换，整个系统状态变为：

其中，是相位的二进制估算值。

最后，对计数寄存器进行测量。图中的与实际上是等价的，当为整数时，二者相等，否则是最佳近似。其等价推导如下：

另外，由于目标寄存器的状态未发生过变化，所以可以重复利用。

计数寄存器中使用的量子比特数 t 决定了估算的精度，估算值与真实值的误差将小于。如果希望成功概率至少为，通常需要选择个量子比特。例如，要获得 n 比特精度且成功概率至少为0.9，大约需要 t=n+3 个量子比特。

相位估计算法本身非常强大，在实现指数级加速与量子并行性的同时拥有可控且高效的精度，但它大部分时候更像是一个子程序，被用于许多著名的量子算法中，比如之后将要学习的用于大数质因数分解shor算法。

3 总结

本周首先进行了上周论文的复现，补充到了一些实现上的细节，比如激活函数有更换之类，但学习的感觉总体比较笼统，可能还需要多积累一些模型，并进行总结；在量子方面，下周将学习shor算法，同时对量子傅里叶变换与量子相位估计进行回顾。