机器学习中的Hello World：线性回归（一）

人工智能与世界模型# 系列文章目录

第一章数学基础（一）导数、偏导数、方向导数与梯度
 第二章数学基础（二）向量、矩阵、行列式与线性变换

第三章机器学习中的Hello World：线性回归（一）

文章目录

[人工智能与世界模型# 系列文章目录](# 系列文章目录)
前言
一、需求引入
二、一元线性回归
- [2.1 假设函数](#2.1 假设函数)
- [2.2 损失函数](#2.2 损失函数)
- [2.3 优化目标](#2.3 优化目标)
- - 最小二乘法（解析解/正规方程）
从零实现正规方程求解线性回归
总结

前言

在人工智能与世界模型的宏大叙事中，我们首先要从最基础、最核心的模型开始。如果说编程世界的"Hello World"是打印一句"Hello World"，那么在机器学习领域，线性回归（Linear Regression）就是那个入门的基石。

线性回归不仅是理解机器学习流程的起点。它的核心思想是：找到一个最合适的线性函数，来拟合输入数据与输出数据之间的关系。

本文将平衡理论推导与代码实践，带你彻底掌握线性回归的数学原理、求解方法，并用 Python/Numpy 从零实现它。

一、需求引入

现在你收集了一些房屋的平米数和价格数据，你想通过这些数据进行分析，实现给你任意一个平米数对于其价格进行预测

假设其平米数与价格的关系图如下：

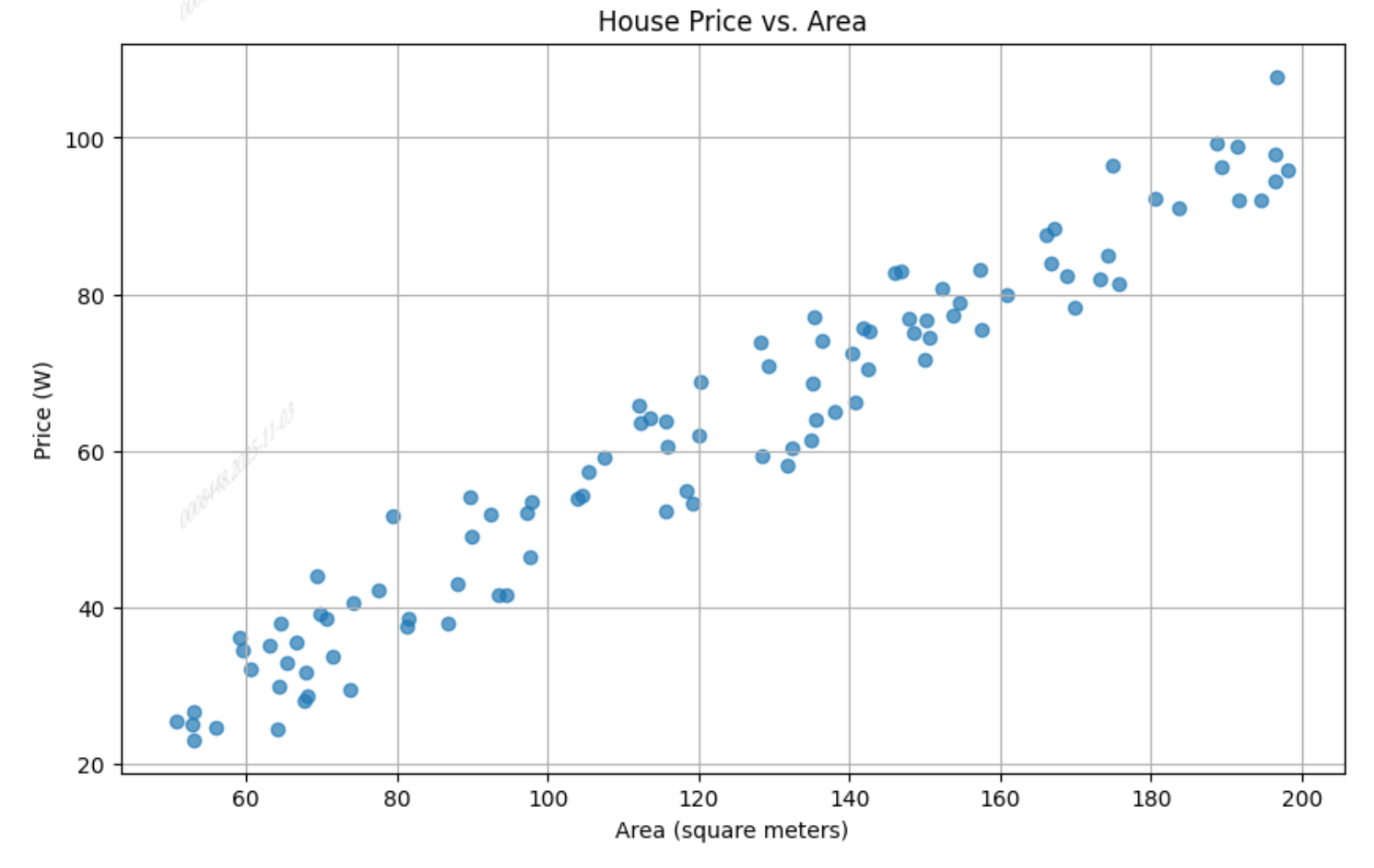
下面，我们将通过这批数据对此功能进行拆解分析实现

二、一元线性回归

2.1 假设函数

根据上面的关系图不难看出，数据中房子的平米数与价格基本呈线性关系。

因此我们可以假设：

P r i c e = w ∗ A r e a + b Price = w * Area + b Price=w∗Area+b

其中w和b为未知数，由此，我们只要确定了w和b的值，就可以完成需求的功能。

将其进行通用化处理，就得到了一元线性回归假设函数：

H ( x ) = w ⋅ x + b H(x) = w·x+b H(x)=w⋅x+b

2.2 损失函数

现在的任务是找到最为合适的w和b，最为粗暴的方法其实是，暴力遍历，即挨个试。虽说这种方式的效率低下，但是确实是可以在一定程度上解决的。

但即便是用暴力破解的方法，依旧存在一个问题，即什么样的w和b是好的，如何评估这种好坏？

我们通常说图一的w和b是好的，而图二是一个糟糕的

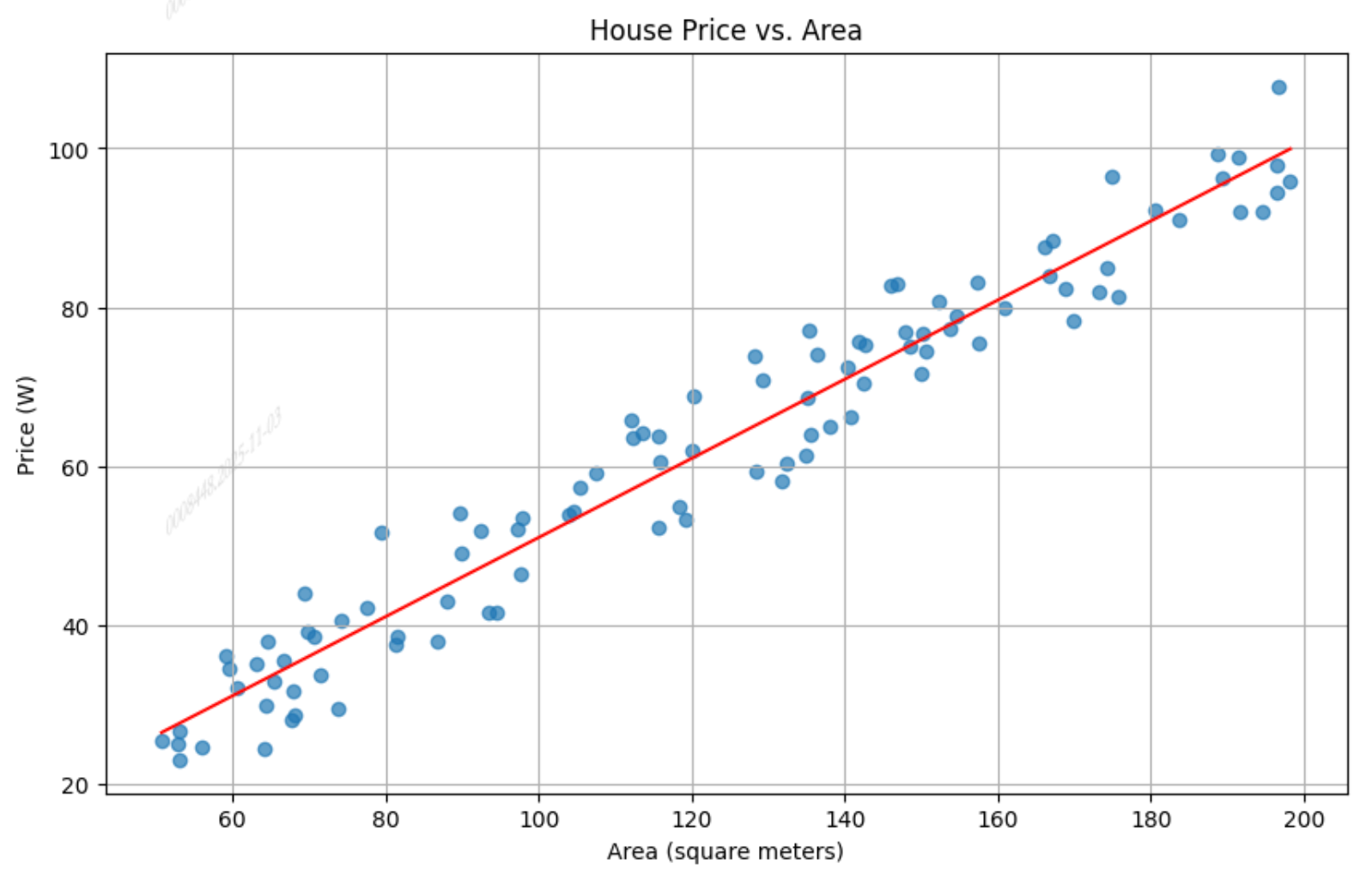
图一

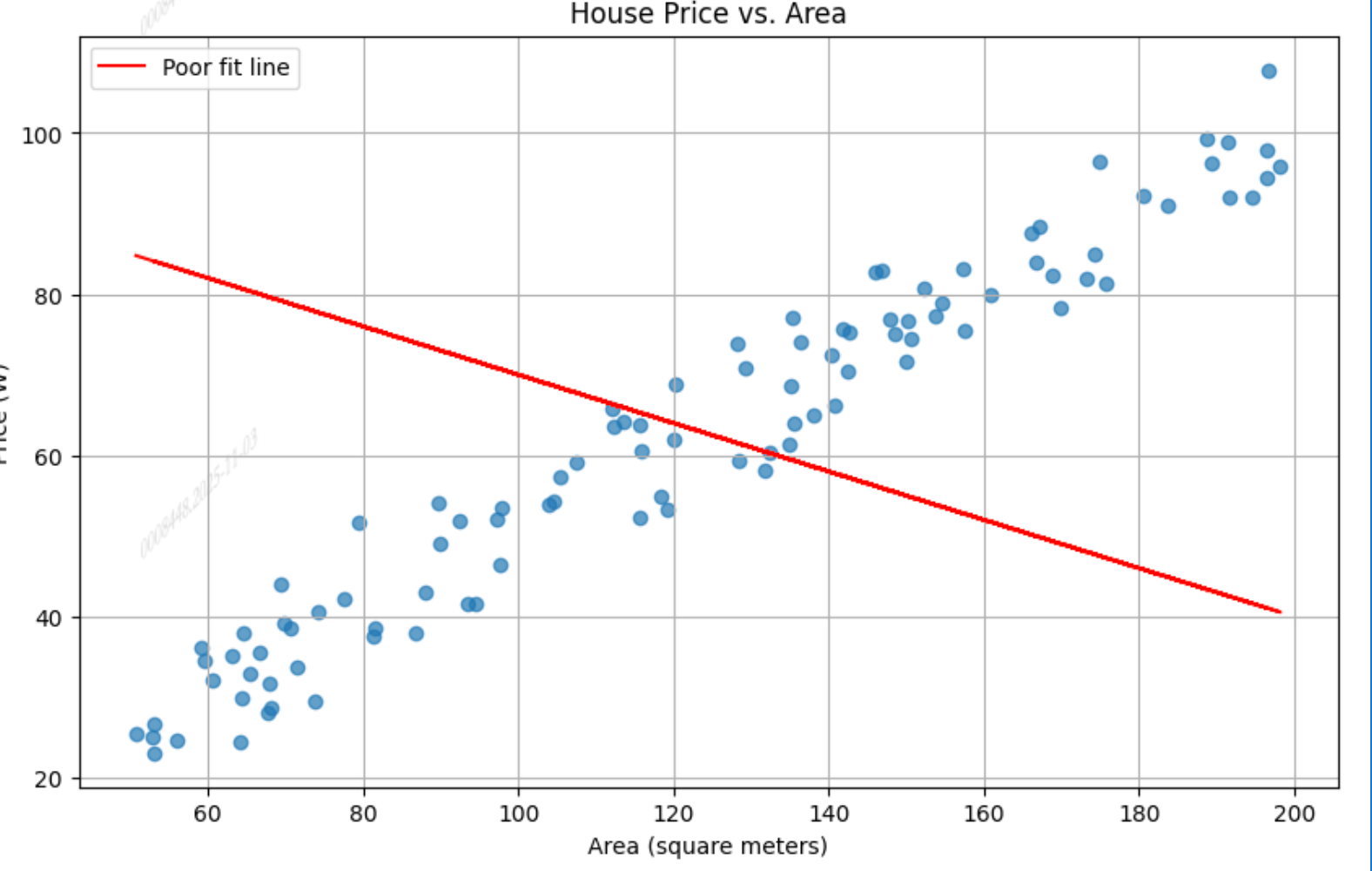
图二

这很直观，但是这样的东西计算机是看不懂的，我们必须对其进行量化，为什么图一比图二好，好多少，我们需要一个指标进行评估。

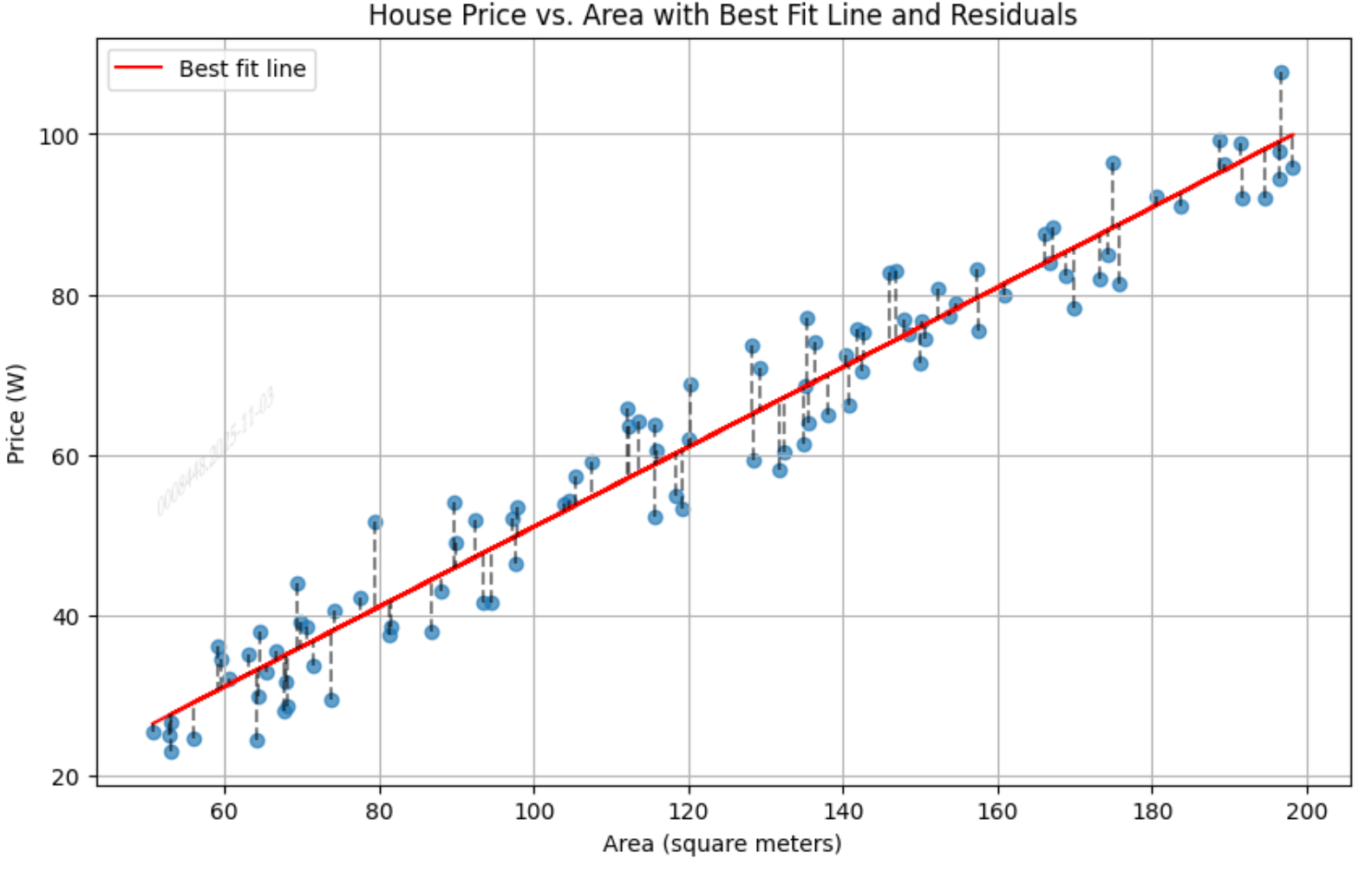
如上图所示，每个数据点到回归线的距离是该数据点预测值和真实值的偏差。

e i = ∣ H ( x i ) − y i ∣ e_i = |H(x_i) - y_i| ei=∣H(xi)−yi∣

然而，一个公式或者函数存在绝对值，对于后续的计算是相对麻烦的。绝对值在其中的意义为确保所有数为正数，因此我们可以换一种保证结果为正的计算方式---平方。

平方对比绝对值的优点：

绝对值会使整个函数变复杂
绝对值存在一点不可导
平方会放大偏差较大的项

因此变形后的偏差为

e i = ( H ( x i ) − y i ) 2 e_i = (H(x_i) - y_i)^2 ei=(H(xi)−yi)2

所有数据的平均偏差为：

e = 1 m ∑ i = 1 m ( H ( x i ) − y i ) 2 e = \frac{1}{m}\sum_{i=1}^{m}(H(x_i) - y_i)^2 e=m1∑i=1m(H(xi)−yi)2

e便能用于评估w和b好不好，e越小，w和b越好；反之，则越糟糕。

这种评估一个拟合的好与坏的函数则被称之为损失函数。

而e稍加修饰则是线性回归中最常用的损失函数---均方误差（MSE）：

L ( w , b ) = 1 2 m ∑ i = 1 m ( H ( x i ) − y i ) 2 L(w, b) = \frac{1}{2m} \sum_{i=1}^{m} (H(x_i) - y_i)^2 L(w,b)=2m1∑i=1m(H(xi)−yi)2

1 2 \frac{1}{2} 21 是为了在求导时抵消平方项产生的 2，方便计算，不影响最终结果。
L ( w , b ) L(w, b) L(w,b) 是关于 w, b 的函数，我们称之为损失函数。

2.3 优化目标

我们的核心任务就是找到一组最优的权重 w , b w, b w,b，使得损失函数 L ( w , b ) L(w, b) L(w,b) 达到最小值：

( w , b ) ∗ = arg ⁡ min ⁡ w , b L ( w , b ) (w, b)^* = \arg \min_{w, b} L(w, b) (w,b)∗=argminw,bL(w,b)

由于 L ( w , b ) L(w, b) L(w,b) 是一个关于 w , b w, b w,b 的凸函数（碗状），它只有一个全局最小值，因此我们可以放心使用优化算法来寻找这个最低点。

优化方式分为两种：一种是计算解析解，一种是计算迭代解（下一章的多元线性回归讲）

最小二乘法（解析解/正规方程）

最小二乘法（Ordinary Least Squares, OLS）是一种解析解方法，它通过直接求解方程来一步到位地找到最优解。

原理：要找到 L ( w , b ) L(w, b) L(w,b) 的最小值，我们只需要对 w , b w, b w,b 求偏导，并令导数等于零。

∂ L ( w , b ) ∂ w = 1 m ∑ i = 1 m ( ( w x i + b − y i ) x i ) = 0 \frac{\partial L(w, b)}{\partial w} = \frac{1}{m}\sum_{i=1}^{m}((wx_i+b-y_i)x_i) = 0 ∂w∂L(w,b)=m1∑i=1m((wxi+b−yi)xi)=0

∂ L ( w , b ) ∂ b = 1 m ∑ i = 1 m ( w x i + b − y i ) = 0 \frac{\partial L(w, b)}{\partial b} = \frac{1}{m}\sum_{i=1}^{m}(wx_i+b-y_i) = 0 ∂b∂L(w,b)=m1∑i=1m(wxi+b−yi)=0

推导结果（正规方程 Normal Equation）：经过矩阵求导和代数运算，我们可以直接得到最优权重 ( w , b ) ∗ (w, b)^* (w,b)∗ 的表达式：

w ∗ = ∑ i = 1 m x i y i − x i b ∑ i = 1 m x i w^* = \frac{\sum_{i=1}^{m}x_iy_i-x_ib}{\sum_{i=1}^{m}x_i} w∗=∑i=1mxi∑i=1mxiyi−xib

b ∗ = ∑ i = 1 m y i − w x i m b^* = \frac{\sum_{i=1}^{m}y_i - wx_i}{m} b∗=m∑i=1myi−wxi

从零实现正规方程求解线性回归

python 复制代码

def get_data():
    # 设置随机数种子以便结果可复现
    np.random.seed(0)
    
    # 生成房屋面积数据（平米），范围从50到200平米
    area = np.random.uniform(50, 200, 100)
    
    # 假设基础价格为每平米5000元，并且加入一些随机性来模拟真实情况
    # 这里我们给价格添加了一个与面积相关的非线性项和一些随机噪声
    price_per_square_meter = 5000
    nonlinear_effect = area * 0.6 - (area - 125) ** 2 * 0.004  # 添加非线性影响
    noise = np.random.normal(0, 50000, size=area.shape)  # 随机噪声
    price = (area * price_per_square_meter + nonlinear_effect + noise) / 10000
    return area, price

# 正规方程求解线性回归
class LinearRegressionOLS:
    def __init__(self):
        # 初始化随机一个w和b
        self.w = np.random.normal(0, 1)
        self.b = np.random.normal(0, 1)

    def fit(self, x, y):
        # 使用正规方程求得最优的w和b
        self.w = np.sum((x * y) - (x * self.b)) / np.sum(x**2)
        self.b = np.sum(y - (self.w * x)) / len(x)

    def predict(self, x):
        return self.w * x + self.b

    def cal_MSE(self,x, y):
        # 计算当前的mse
        return np.sum((self.predict(x) - y) ** 2) / (2 * len(x))

model = LinearRegressionOLS()
x, y = get_data()
print("优化之前的mse：")
print(model.cal_MSE(x, y))
model.fit(x, y)
print("优化之后的mse：")
print(model.cal_MSE(x, y))

# 绘制散点图以及最佳拟合线
plt.figure(figsize=(10, 6))
plt.scatter(x, y, alpha=0.7)
plt.title('House Price vs. Area with Best Fit Line and Residuals')
plt.xlabel('Area (square meters)')
plt.ylabel('Price (W)')
plt.grid(True)

# 使用这个最好的模型计算预测值
price_predicted_best = model.predict(x)

# 在图中添加这条"最佳"的拟合线
plt.plot(area, price_predicted_best, color='red', label='Best fit line')

运行结果：

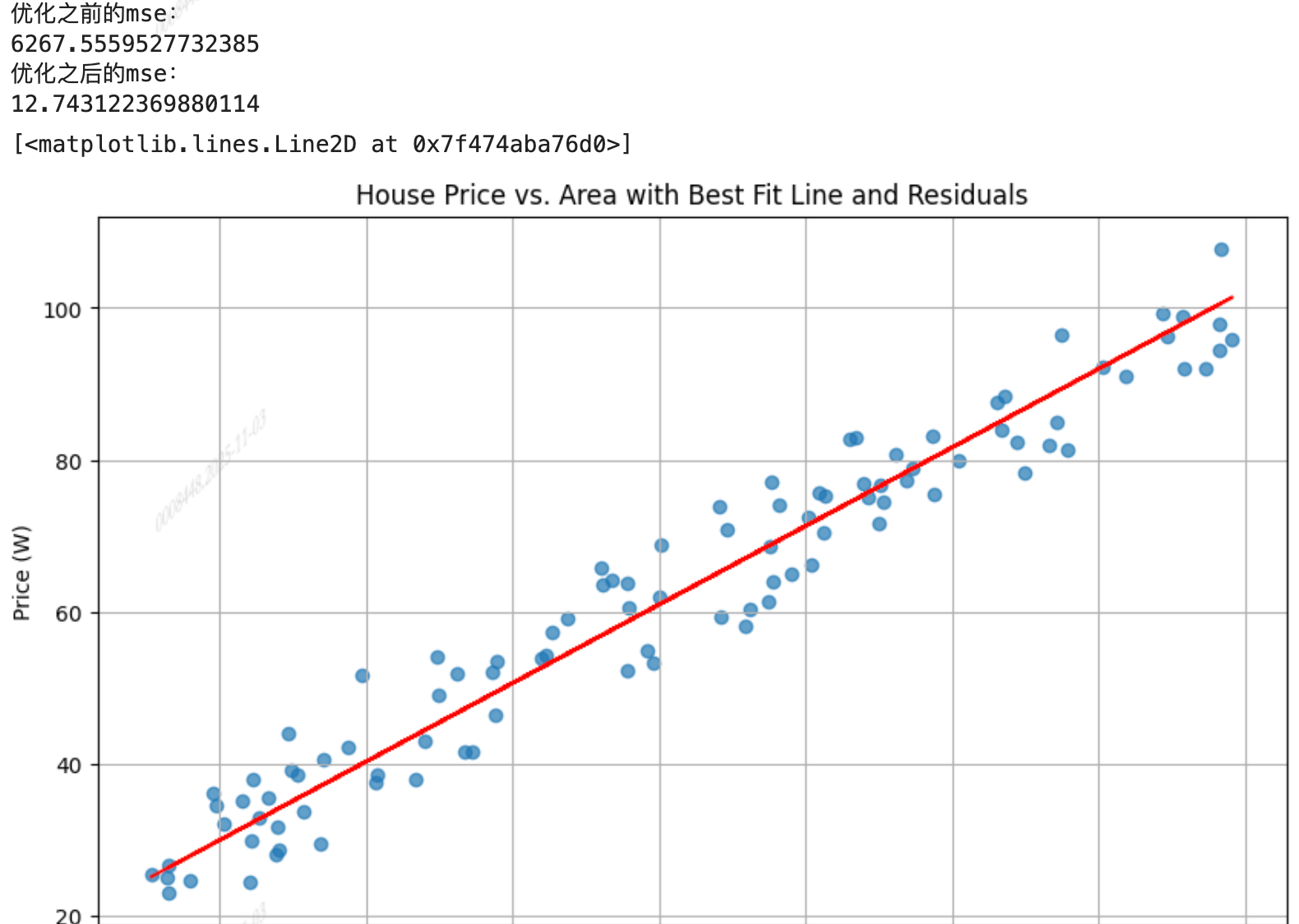
总结

本文对于单元线性回归进行了系统的拆解讲述，由于篇幅问题多元线性回归放在下一个章节。