INT303 Big Data Analysis 大数据分析 Pt.3 数据挖掘（Data Mining）

文章目录

• [1. 前情总结](#1. 前情总结)
• • [1.1 什么是数据挖掘](#1.1 什么是数据挖掘)
  • [1.2 数据类型](#1.2 数据类型)
• [2. 数据挖掘的流程/数据挖掘管道（Data Mining Pipeline）](#2. 数据挖掘的流程/数据挖掘管道（Data Mining Pipeline）)
• • [2.1 数据收集（Data Collection）](#2.1 数据收集（Data Collection）)
  • • [2.1.1 数据标签（Data labels）](#2.1.1 数据标签（Data labels）)
  • [2.2 数据预处理（Preprocessing）](#2.2 数据预处理（Preprocessing）)
  • • [2.2.1 采样（sampling）](#2.2.1 采样（sampling）)
    • • [2.2.1.1 采样方法](#2.2.1.1 采样方法)
      • [2.2.1.2 样本大小](#2.2.1.2 样本大小)
      • [2.2.1.3 降维](#2.2.1.3 降维)
    • [2.2.2 数据清洗（Data cleaning）](#2.2.2 数据清洗（Data cleaning）)
    • • [2.2.2.1 处理噪声](#2.2.2.1 处理噪声)
      • [2.2.2.2 处理兼容性](#2.2.2.2 处理兼容性)
      • [2.2.2.3 处理缺失值](#2.2.2.3 处理缺失值)
      • [2.2.2.4 处理异常值](#2.2.2.4 处理异常值)
      • [2.2.2.5 注意](#2.2.2.5 注意)
    • [2.2.3 特征提取（feature extraction）](#2.2.3 特征提取（feature extraction）)
    • • [2.2.3.1 文本数据](#2.2.3.1 文本数据)
      • • [2.2.3.1.1 文本规范化（Text normalization）](#2.2.3.1.1 文本规范化（Text normalization）)
        • [2.2.3.1.2 TF-IDF表示法](#2.2.3.1.2 TF-IDF表示法)
        • [2.2.3.1.3 词嵌入（Word Embeddings）](#2.2.3.1.3 词嵌入（Word Embeddings）)
    • [2.2.4 数据规范化](#2.2.4 数据规范化)
    • • [2.2.4.1 列规范化（Column Normalization）](#2.2.4.1 列规范化（Column Normalization）)
      • • [2.2.4.1.1 特征中心化（Centering of features）](#2.2.4.1.1 特征中心化（Centering of features）)
        • [2.2.4.1.2 Z得分规范化（Z-score normalization）](#2.2.4.1.2 Z得分规范化（Z-score normalization）)
      • [2.2.4.2 行规范化（Row Normalization）](#2.2.4.2 行规范化（Row Normalization）)
      • • [2.2.4.2.1 特征中心化（Centering of features）](#2.2.4.2.1 特征中心化（Centering of features）)
        • [2.2.4.2.2 Z得分规范化（Z-score normalization）](#2.2.4.2.2 Z得分规范化（Z-score normalization）)
        • [2.2.4.2.3 Softmax函数](#2.2.4.2.3 Softmax函数)
        • [2.2.4.2.4 逻辑函数（Logistic function）](#2.2.4.2.4 逻辑函数（Logistic function）)
        • [2.2.4.2.5 激活函数（Sigmoid function）](#2.2.4.2.5 激活函数（Sigmoid function）)
        • [2.2.4.2.6 对数函数（Logarithm function）](#2.2.4.2.6 对数函数（Logarithm function）)
    • [2.2.5 数据预处理的建议](#2.2.5 数据预处理的建议)
  • [2.3 数据后处理（Post-Processing）](#2.3 数据后处理（Post-Processing）)
  • • [2.3.1 数据可视化（Visualization）](#2.3.1 数据可视化（Visualization）)
    • • [2.3.1.1 非线性降维（Non-linear dimensionality reduction）](#2.3.1.1 非线性降维（Non-linear dimensionality reduction）)
    • [2.3.2 统计显著性（Statistical Significance）](#2.3.2 统计显著性（Statistical Significance）)
    • [2.3.3 没有实际意义的发现](#2.3.3 没有实际意义的发现)

1. 前情总结

1.1 什么是数据挖掘

数据挖掘是研究如何收集、处理、分析数据并从中获得有用见解。

任何与数据相关的活动都可以被视为数据挖掘的一部分。

1.2 数据类型

数值数据（Numeric data）：

每个对象可以被视为多维空间中的一个点。这意味着每个对象都有多个数值属性，这些属性可以看作是多维空间中的坐标。

分类数据（Categorical data）：

每个对象是一个分类值的向量。这意味着对象的属性是分类的，比如颜色、性别、品牌等。

集合数据（Set data）：

每个对象是一个值的集合，可以包含计数信息，也可以不包含。例如，一个购物篮中的商品集合。

集合数据的表示：

集合也可以表示为二进制向量或计数向量。二进制向量中的每个元素表示集合中是否包含某个值，而计数向量则表示每个值出现的次数。

依赖数据（Dependent data）：

这类数据包含有顺序的序列，每个对象是一个有序的值序列。

空间数据（Spatial data）：

对象固定在特定的地理位置上，比如地图上的点。

图数据（Graph data）：

是一系列成对关系（边）的集合，通常由节点（顶点）和连接这些节点的边组成。

数据矩阵（The data matrix）：

几乎所有类型的数据都可以转换成一个矩阵形式，其中行对应于不同的记录（例如，不同的观测或对象），列对应于数值属性（例如，不同的特征或变量）。

2. 数据挖掘的流程/数据挖掘管道（Data Mining Pipeline）

虽然说到数据挖掘我们主要想到的是数据分析部分，但是其实它有多个环节组成。

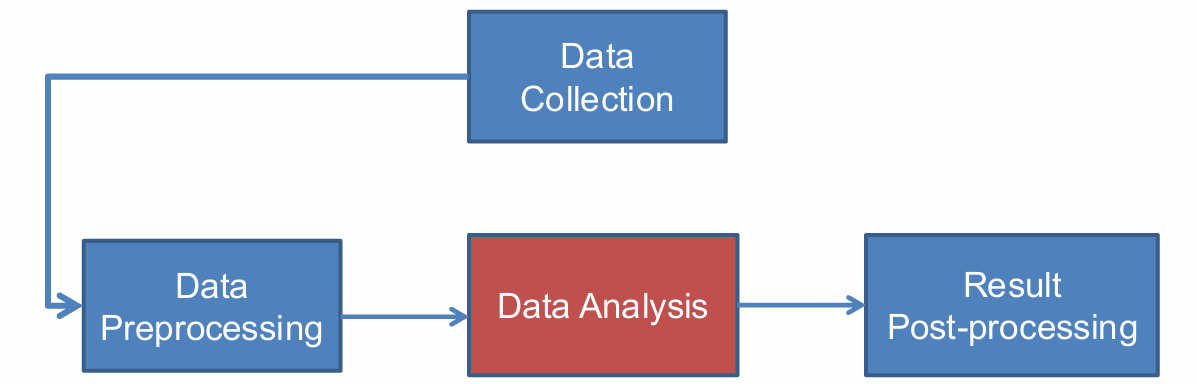
数据挖掘流程的第一步是数据收集，涉及从各种来源收集原始数据。

在收集到数据后，需要进行预处理。这可能包括数据清洗（去除错误或不完整的数据）、数据集成（合并来自不同来源的数据）、数据选择（选择与分析任务相关的数据子集）以及数据变换（将数据转换成适合挖掘的形式）。

然后是数据分析，涉及应用各种方法和算法来从数据中提取有用的知识。这可能包括分类、聚类、关联规则学习等。

分析完成后，需要对结果进行后处理，这可能包括结果的解释、可视化以及将结果转化为可操作的洞察。

在本课程中，将主要关注数据分析部分，即如何使用方法和算法从数据中提取有用的知识。

2.1 数据收集（Data Collection）

获取数据有多种方法：

1. 生成自己的数据（Generate your own data）：
   你可以通过记录某个过程或活动来生成数据，例如科学测量。
   重要的是要收集适量且相关的信息，以确保数据的质量和分析的有效性。
2. 使用现有的数据集合（Use existing collections）：
   现在网络上有许多可用的数据集合，包括开放数据、企业数据发布、维基百科和科学数据共享等。
   需要注意的是，现有的数据集合可能受到创建者所做的某些选择的影响，这些选择可能会影响数据的代表性和分析结果。
3. 在线获取数据（Obtaining data online）：
   公共API（Public APIs）：许多在线平台（如Twitter）提供API，允许在一定限制下访问他们的数据。通过这种方式，你可以快速获得结构化数据。
   爬虫和抓取（Crawling & Scraping）：使用程序遍历网页并下载它们（爬虫），然后从下载的内容中提取有用信息（抓取）。
   在进行爬虫操作时，应该遵守网络爬虫的礼仪，尊重网站的robots.txt文件和其他使用条款，以避免对网站造成不必要的负担。
   这种方法可能会遇到一些问题，如网页布局经常变化，导致抓取的数据可能不准确或不稳定。

2.1.1 数据标签（Data labels）

在监督学习中，模型需要使用带有标签的数据进行训练和测试。这些标签提供了数据的真实类别或属性，帮助模型学习如何正确分类或预测。

这里给出一些例子：

推文分类：对一组推文进行标签标注，标记为"冒犯性"或"非冒犯性"。

情感分析：对一组句子进行标签标注，标记为对某个特定项目有"积极"、"消极"或"中性"的情感。

搜索结果相关性：对一组搜索结果进行标签标注，标记为与查询"相关"或"不相关"。

这些标签代表了我们试图预测的"真实情况"或"真实类别"。在训练模型时，这些标签帮助模型了解哪些预测是正确的，哪些是错误的。

获取准确的数据标签通常是一个困难的任务，因为它需要人工进行标注。这可能涉及到复杂的判断和专业知识，尤其是在处理模糊或主观的分类时。

由于标注工作的重要性和复杂性，许多公司会雇佣专门的工作人员来进行数据标注。这些工作人员可能需要接受培训，以确保他们能够准确地理解和应用标签标准。

2.2 数据预处理（Preprocessing）

真实世界中的数据通常具有以下特点：

庞大（Large）：数据量通常非常大，可能包含数百万甚至数十亿条记录。

噪声（Noisy）：数据中可能包含错误、异常值或不准确的信息。

不完整（Incomplete）：数据可能缺少某些属性或字段，导致信息不完整。

不一致（Inconsistent）：数据可能在格式、单位或命名等方面存在不一致性。

由于真实数据存在上述问题，我们需要在将其用于数据挖掘或分析之前进行预处理，以提高数据的质量和可用性。

预处理步骤决定了数据挖掘算法的输入数据。高质量的预处理可以提高算法的性能和准确性。

预处理通常是数据分析中最重要的步骤之一。良好的预处理可以显著提高分析结果的可靠性和有效性。

尽管预处理非常重要，但它通常被认为是一项繁琐、耗时且可能不那么吸引人的工作。然而，这是数据分析过程中必不可少的一部分，需要有人来完成。

数据预处理的三个主要步骤：

1. 减少数据量（Reducing the data）：

   采样（Sampling）：由于数据量可能非常大，直接处理所有数据可能不现实或不必要。采样是从大数据集中选择一个代表性的子集，以减少需要处理的数据量，同时尽量保留数据的整体特征。

   降维（Dimensionality Reduction）：在数据集中可能存在许多特征，但并非所有特征都对分析有用。降维技术旨在减少特征的数量，例如通过主成分分析（PCA）等方法，以简化模型并减少计算复杂性。

2. 数据清洗（Data cleaning）：

   这一步骤涉及处理数据中的缺失值或不一致信息。例如，填充缺失值、纠正错误数据、标准化数据格式等。数据清洗的目的是确保数据的准确性和一致性，从而提高分析结果的可靠性。

3. 特征提取和选择（Feature extraction and selection）：

   特征提取（Feature extraction）：从原始数据中创建新的特征，这些特征可能更能代表数据的本质或对分析任务更有用。例如，从时间序列数据中提取趋势或季节性特征。

   特征选择（Feature selection）：从现有特征中选择最相关的特征，以创建数据的有效表示。这有助于减少噪声、提高模型性能，并使模型更易于解释。

2.2.1 采样（sampling）

采样是用于数据选择的主要技术。它涉及从更大的数据集中选择一个较小的、代表性的子集。

采样不仅用于数据的初步调查，也用于最终的数据分析。通过采样，可以在不处理整个数据集的情况下，对数据进行探索和分析。

统计学家进行采样是因为获取整个感兴趣的数据集可能过于昂贵或耗时。采样可以减少所需的资源和时间。

例如，要计算英国人的平均身高，不可能测量每个人的身高。通过采样，可以从总体中选择一部分人进行测量，然后用这些数据来估计整个群体的平均身高。

在数据挖掘中，处理整个感兴趣的数据集可能同样昂贵或耗时。采样可以减少计算量和资源消耗。

例如，如果有100万个文档，要计算有多少对文档至少有100个共同词汇，需要进行10^12次比较。通过采样，可以减少需要比较的文档对数量。

如果每天有5亿条推文，平均每条100个字符，那么一年的数据量将达到86.5TB。要分析所有推文以找出包含"UK"这个词的比例，通过采样可以显著减少所需的存储和处理资源。

有效采样的核心原则是：如果样本具有代表性，那么使用样本几乎可以像使用整个数据集一样有效。

那什么是代表性呢？

一个样本具有代表性，如果它大致具有与原始数据集相同的属性（我们感兴趣的属性）。

如果样本不具有代表性，那么它可能会引入一些偏差。偏差是指样本不能准确反映总体的特征，从而导致分析结果不准确或有误导性。

回到前面的身高例子，如果我们从伦敦的一所大学校园中抽取样本来计算伦敦人的平均身高，那么这个样本可能不具有代表性，因为它只代表了伦敦人口的一个特定子集（大学生）。

2.2.1.1 采样方法

采样方法有多种：

1. 简单随机抽样（Simple Random Sampling）：
   在简单随机抽样中，每个项目被选中的概率是相等的。这是一种最基本的抽样方法，确保了样本的代表性。
2. 有放回抽样（Sampling with replacement）：
   在有放回抽样中，每次抽取一个样本后，将其放回总体中，然后再进行下一次抽取。这意味着同一个样本可以被多次抽取。
   这种方法在计算概率时更为简单，因为每次抽取都是独立的。
3. 无放回抽样（Sampling without replacement）：
   在无放回抽样中，一旦一个样本被抽取，它就不会被放回总体中，因此在后续的抽取中不会被再次选中。
   这种方法更接近实际情况，但计算概率时需要考虑样本被抽取后对总体的影响。

下面我们将有放回和无放回进行对比：

假设有 100 100 100个人，其中 51 51 51个是女性（ P ( W ) = 0.51 P(W) = 0.51 P(W)=0.51）， 49 49 49个是男性（ P ( M ) = 0.49 P(M) = 0.49 P(M)=0.49）。如果我们抽取两个人，计算两次都抽到女性的概率 P ( W , W ) P(W,W) P(W,W)。

有放回抽样：每次抽取都是独立的，所以两次都抽到女性的概率是 0.51 ∗ 0.51 0.51 * 0.51 0.51∗0.51。

无放回抽样：第一次抽取女性的概率是 51 / 100 51/100 51/100，抽取后剩下 50 50 50个女性和 99 99 99个人，所以第二次抽取女性的概率是 50 / 99 50/99 50/99。因此，两次都抽到女性的概率是 ( 51 / 100 ) ∗ ( 50 / 99 ) (51/100) * (50/99) (51/100)∗(50/99)。

4. 分层抽样（Stratified sampling）：
   分层抽样是一种抽样方法，它将数据分成几个不同的组（或层），然后从每个组中随机抽取样本。这种方法确保了所有组都在样本中得到代表。
   分层抽样确保了数据集中的每个子群体都被考虑到，这对于分析数据中的特定群体特征非常重要。

例子1：假设你想要了解合法和欺诈性信用卡交易之间的区别。如果欺诈性交易只占0.1%，那么随机抽取1000笔交易可能只会得到1笔欺诈性交易（期望值）。

由于欺诈性交易的数量太少，可能无法得出有意义的结论。解决方案是分别抽取1000笔合法交易和1000笔欺诈性交易，这样可以确保两种类型的交易都有足够的样本量进行分析。

例子2：链接在一起的网页是否平均有更多的共同词汇，相比于没有链接的网页？如果你有100万个网页和100万个链接，随机选择1万对网页可能不会得到任何链接。

由于链接的网页对在总体中的比例可能很低，随机抽样可能无法有效捕捉到这些链接。解决方案是随机抽取1万对没有链接的网页和1万对有链接的网页，这样可以确保两种类型的网页对都有足够的样本量进行比较。

5. 有偏采样（Biased sampling）：
   有时候，我们希望我们的样本能够偏向数据的某个特定子集。这样做的目的是为了更深入地研究或分析这个子集的特性。
   分层抽样是一种有偏采样的方法，它通过将数据分成几个不同的组（或层），然后从每个组中随机抽取样本，确保所有组都在样本中得到代表。
   我们再举一个例子，当我们对时间序列数据进行采样时，可能希望增加采样最近数据的概率。这可以通过引入近期偏差（recency bias）来实现，即更倾向于选择最近的数据点。
   我们可以设计采样策略，使采样概率与时间或数据项的年龄有关。例如，让采样概率随时间指数级下降。这意味着随着数据项年龄的增长，其被选中的概率会迅速降低。
   对于在时间 t t t之后的数据项 x t x_t xt，其被选中的概率可以表示为 p ( x t ) ∝ e − t p(x_t)∝e^{−t} p(xt)∝e−t，负指数表示概率随时间的增加而迅速下降。

2.2.1.2 样本大小

假设我们有10个不同的组，为了确保从每个组至少抽取一个对象，需要多大的样本量？

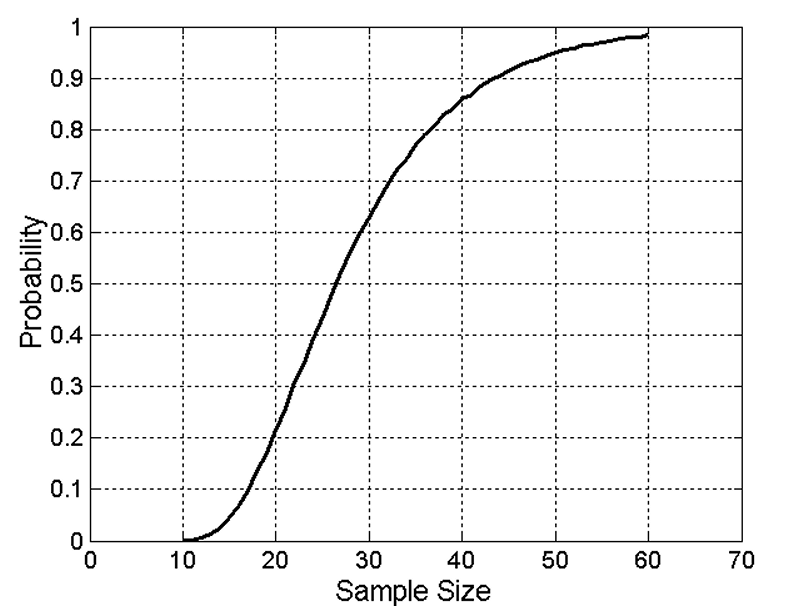
随着样本大小的增加，能够从每个组至少抽取一个对象的概率迅速增加，但这个概率在30左右上升速度很快，在70左右几乎饱和。

2.2.1.3 降维

降维的主要目的是减少数据的维度，即减少数据集中的属性数量。

降维的好处有：

1. 减少数据量。
2. 提取有用信息。

真实世界的数据通常是高维的，可能包含数百、数千甚至数百万的属性。

例如：

文档可以表示为词频向量，每个词是一个维度，可能包含数百万的维度。

Facebook用户可以表示为好友列表向量，每个好友是一个维度，可能包含数十亿的维度。

客户可以表示为购买产品列表向量，每个产品是一个维度，可能包含数十万的维度。

高维数据通常是稀疏的，且包含噪声。

降维技术可以帮助我们通过减少维度来降低数据的稀疏性和噪声的影响。

常见的降维技术包括主成分分析（PCA）、线性判别分析（LDA）、t-分布随机邻域嵌入（t-SNE）等。

例如下面我们给出了一个6维的数据集。

我们可以将其写为下面的式子。

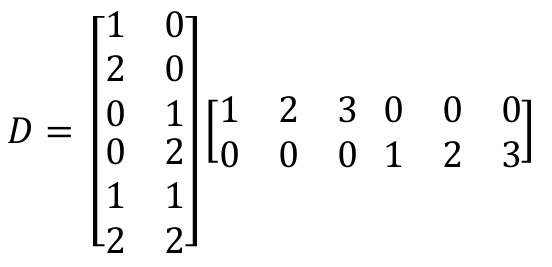
2.2.2 数据清洗（Data cleaning）

有时候我们会遇到数据质量的问题，例如：噪声和异常值（Noise and outliers）、缺失值（Missing values）、重复数据（Duplicate data）。

2.2.2.1 处理噪声

数据清洗是处理噪声数据的一种方法，它涉及识别和修正或删除数据中的错误、不准确或不一致的信息。

当我们拥有大量数据时，我们可以删除那些我们怀疑有问题或认为无用的数据，而不会对整体分析产生太大影响。

数据清洗的具体做法如下：

1. 如果数据集中的某些记录包含缺失值或重复值，我们可以选择删除这些记录。
2. 在某些情况下，极端值或非典型案例可能不代表数据的一般趋势，因此可以选择删除。
   例如：在数据库数据中，如果某些记录的值明显偏离正常范围，这些记录可能被视为异常值并被删除。在推文文本数据中，删除少于3个单词的推文。在交易数据中，删除所有人都购买的产品和很少有人购买的产品。

2.2.2.2 处理兼容性

在进行数据清洗时，我们需要谨慎行事，确保不会错误地删除对分析有用的信息。

在数据清洗过程中，需要解决数据的兼容性问题，确保数据在不同的部分是一致和可比较的。例如数据中可能存在不同的度量单位，需要将这些单位统一，以便进行准确的比较和分析。

时间数据需要统一到同一个时区，以确保时间的一致性。

不同的记录可能包含同一个人的不同姓名表示方式，例如全名、缩写或中间名的变体。需要将这些姓名标准化，以确保它们被识别为同一个人。

财务数据需要标准化，以便于比较和分析，这包括不同货币的统一以及随时间变化的价格。

2.2.2.3 处理缺失值

一种简单的处理缺失值的方法是忽略包含缺失值的记录。这种方法适用于缺失值数量较少的情况，但如果缺失值过多，可能会导致大量数据的丢失，影响分析结果。

我们可以用随机生成的值替换缺失值。这种方法可以帮助理解缺失值对输出结果的影响，但通常不是一个好主意，因为它可能会引入额外的噪声，影响数据的真实性。

还有用该列的均值替换缺失值。这是一种相对常见的做法，尤其是在处理数值型数据时。然而，需要小心使用，因为对于某些数据（如出生年/死亡年），用均值替换可能没有意义。

用与缺失值所在记录最相似的记录（最近邻值）的值来替换缺失值。这种方法基于相似性，适用于那些具有空间或时间邻近性的数据处理。

我们还可以将数据分成不同的簇，然后使用每个簇的均值来替换该簇内记录的缺失值。这种方法适用于数据具有明显分组或分类特征的情况。

我们还能使用统计方法或机器学习模型来推断缺失值。这可能包括使用回归模型、决策树或其他预测模型，根据其他变量的值来预测缺失值。

2.2.2.4 处理异常值

一种简单的处理方法是直接删除包含异常值的记录。这种方法适用于异常值数量较少且对整体数据分析影响不大的情况。

如果异常值可能是由于数据录入错误或其他可识别的原因造成的，可以尝试使用常识来纠正这些值。例如，如果一个数据集中的年龄值出现了300岁，这显然是一个错误，可以将其更正为更合理的值。

通过应用数学转换来减少异常值的影响。常见的转换方法包括对数转换、平方根转换或Box-Cox转换等。

在某些情况下，极端值是预期的并且可能包含重要的信息。例如，在财富分布或社交媒体关注者数量的数据中，极端值可能代表了超级富豪或网红。

当数据分布偏斜时，使用对数转换可以减少极端值的影响，使数据分布更接近正态分布。还可使用分箱（binning），分箱是将连续变量分成不同的区间或"箱子"，这有助于减少异常值的影响，并使数据更易于分析。

2.2.2.5 注意

在使用数据进行分析时，需要保持警惕，特别是当结果看起来"好得令人难以置信"或者"坏得令人难以置信"的时候，我们需要重新检查数据收集和输入的过程，确保数据的准确性和完整性，还需要确定我们再数据清洗时是否有处理不当，验证分析方法是否选择正确。

2.2.3 特征提取（feature extraction）

我们获取的数据可能不是以关系型表格的形式存在。数据可能以非常原始的格式出现（包括文本、语音、鼠标移动等非结构化数据），需要进一步处理才能用于分析。

特征提取的目标是从原始数据中提取特征（或属性），并将这些特征组织成一个数据矩阵，其中行通常代表不同的记录（例如，不同的观测或对象），列代表不同的特征。

特征提取需要领域知识来确定哪些特征对于分析任务是重要的。不同的应用可能需要不同的特征集。

深度学习是一种强大的机器学习方法，它可以在特征提取步骤中提供帮助。深度学习模型，如卷积神经网络（CNN）用于图像处理，循环神经网络（RNN）用于序列数据处理，能够自动从原始数据中学习到有用的特征表示。

2.2.3.1 文本数据

文本数据通常不会以整洁的关系型表格形式出现。文本数据是原始的、非结构化的，可能包含大量的自由格式文本。

例子包括电子邮件、社交媒体帖子、新闻文章、客户反馈、书籍等。

由于文本数据是非结构化的，我们需要付出额外的努力来提取文本中的有用信息。这通常涉及到文本处理和自然语言处理（NLP）技术。

处理文本数据时，可以采用一些基本的文本处理方法，这些方法包括：

分词（Tokenization）：将文本分割成单词、短语或其他有意义的元素。

去除停用词（Removing stop words）：删除常见的、对分析没有太大帮助的词，如"和"、"是"、"在"等。

词干提取（Stemming）或词形还原（Lemmatization）：将单词还原为其基本形式，以减少单词的变化形式。

向量化（Vectorization）：将文本转换为数值形式，以便机器学习模型可以处理。常见的向量化技术包括词袋模型（Bag of Words）、TF-IDF（Term Frequency-Inverse Document Frequency）和Word Embeddings（如Word2Vec或GloVe）。

情感分析（Sentiment analysis）：确定文本的情感倾向，如正面、负面或中性。

主题建模（Topic modeling）：识别文本集合中的主题或模式。

例如我们分析各平台的对餐厅的评论数据提取出描述餐厅的关键术语，如食物质量、服务速度、环境和位置等。

正式开始前，我们的步骤和前面一致，需要先决定收集哪些数据、收集多少数据以及收集数据的时间跨度。再决定如何进行数据清理。还要考虑对不同部分的数据进行加权，因为不同的数据可能对分析结果有不同的影响。这些巨册都应该清楚说明，因为它们都会影响结果。

2.2.3.1.1 文本规范化（Text normalization）

每条评论最初可能都是一个长字符串。为了进行文本分析，需要将这些字符串转换成单词序列。

这里的预处理包括：

规范化数据（normalize the data）：去除标点符号、将所有文本转换为小写、清除多余的空格等，以减少文本的变异性并简化分析过程。

分词（Break into words）：将文本字符串分割成单独的单词或标记，这是文本分析的基本单位。

有许多现成的库和工具可以自动执行这些预处理步骤，如Python的NLTK、spaCy、TextBlob等，这些库提供了强大的文本处理功能。

又是我们也可以使用n-gram分析，n-gram是指连续的n个单词的组合。分析n-gram可以帮助理解文本中单词的上下文关系，这对于某些文本分析任务（如语言模型、机器翻译等）非常有用。

回到前面的例子，我们先进行文本规范化、分词。

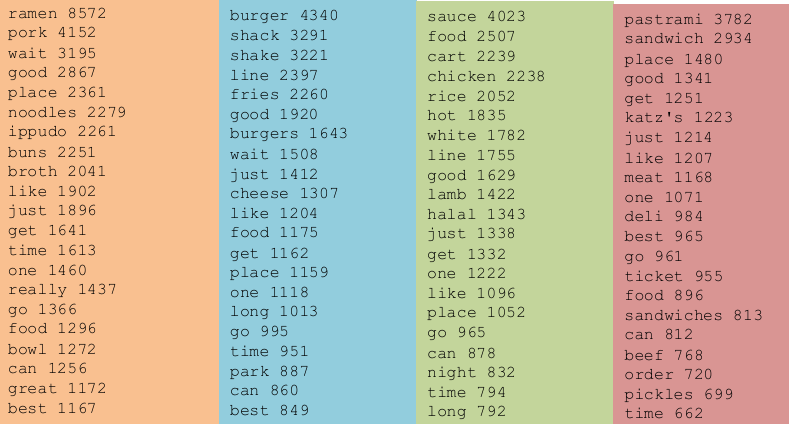
再去掉停用词（stop words），这些词在文本中频繁出现但对分析意义不大。

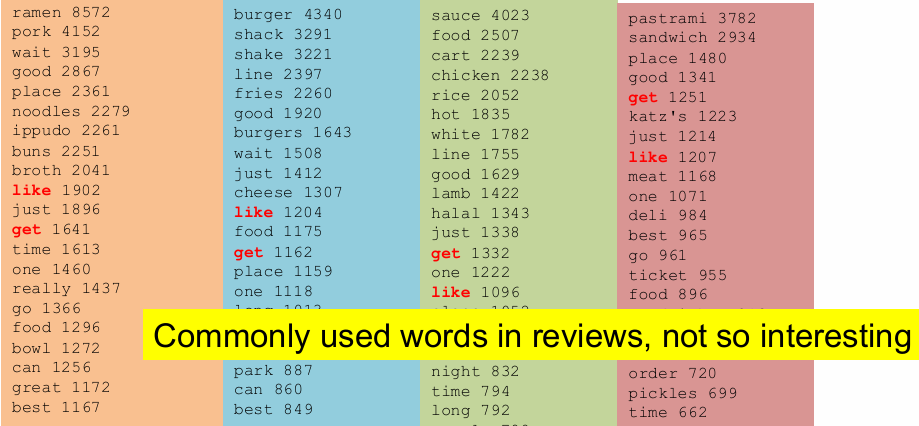
2.2.3.1.2 TF-IDF表示法

重要词语是指那些在特定文档中频繁出现，但在整个文档集合中不常见的词语。这些词语有助于区分一个文档与其他文档的不同。

文档频率是指包含特定词语 w w w的文档数量。公式为 D F ( w ) = D ( w ) D DF(w) = \frac{D(w)}{D} DF(w)=DD(w)，其中 D ( w ) D(w) D(w)是包含词语 w w w的文档数量， D D D是文档集合中的总文档数量。

逆文档频率是一种权重计算方式，用于评估词语在文档集合中的重要性。公式为 I D F ( w ) = log ⁡ ( 1 D F ( w ) ) IDF(w) = \log\left(\frac{1}{DF(w)}\right) IDF(w)=log(DF(w)1)。

当一个词语在很多文档中都出现时，它的 D F ( w ) DF(w) DF(w)值会很高，导致 I D F ( w ) IDF(w) IDF(w)值很低，这意味着这个词语对于区分文档的重要性较低。

相反，如果一个词语只在少数文档中出现，它的 D F ( w ) DF(w) DF(w)值会很低，导致 I D F ( w ) IDF(w) IDF(w)值很高，这意味着这个词语对于区分文档具有较高的重要性。

当一个词语只在一个文档中出现时，它的 I D F ( w ) IDF(w) IDF(w)值达到最大，即 I D F ( w ) = l o g ( D ) IDF(w)=log(D) IDF(w)=log(D)。

当一个词语在所有文档中都出现时，它的 I D F ( w ) IDF(w) IDF(w)值为最小，即 I D F ( w ) = 0 IDF(w)=0 IDF(w)=0。

词频 T F ( w , d ) TF(w,d) TF(w,d)是指词语 w w w在文档 d d d中出现的次数。

TF-IDF权重是词频和逆文档频率的乘积： T F − I D F ( w , d ) = T F ( w , d ) × I D F ( w ) TF-IDF(w,d)=TF(w,d)×IDF(w) TF−IDF(w,d)=TF(w,d)×IDF(w)。

因此，词频（TF）：如果一个词语在文档中出现的频率高，那么它可能对文档的内容有较高的描述能力。

逆文档频率（IDF）：如果一个词语在很多文档中都出现，那么它对区分不同文档的能力就较低；相反，如果它只在少数文档中出现，那么它对区分文档的能力就较高。

我们回到前面的例子进行第三次裁剪，使用TF-IDF来进一步处理文本数据。TF-IDF自动处理停用词，因为这些词在许多文档中都会出现，导致它们的IDF值较低，从而在TF-IDF计算中权重较小。

IDF值依赖于文档集合。在某些特定的文档集合中，一些常见的词语（如"get"、"like"、"eat"）可能对分析非常重要，因此不应简单地将它们视为停用词并去除。

总的来说，这张幻灯片强调了TF-IDF在文本数据预处理。

因此刚刚的例子的整体过程如下。

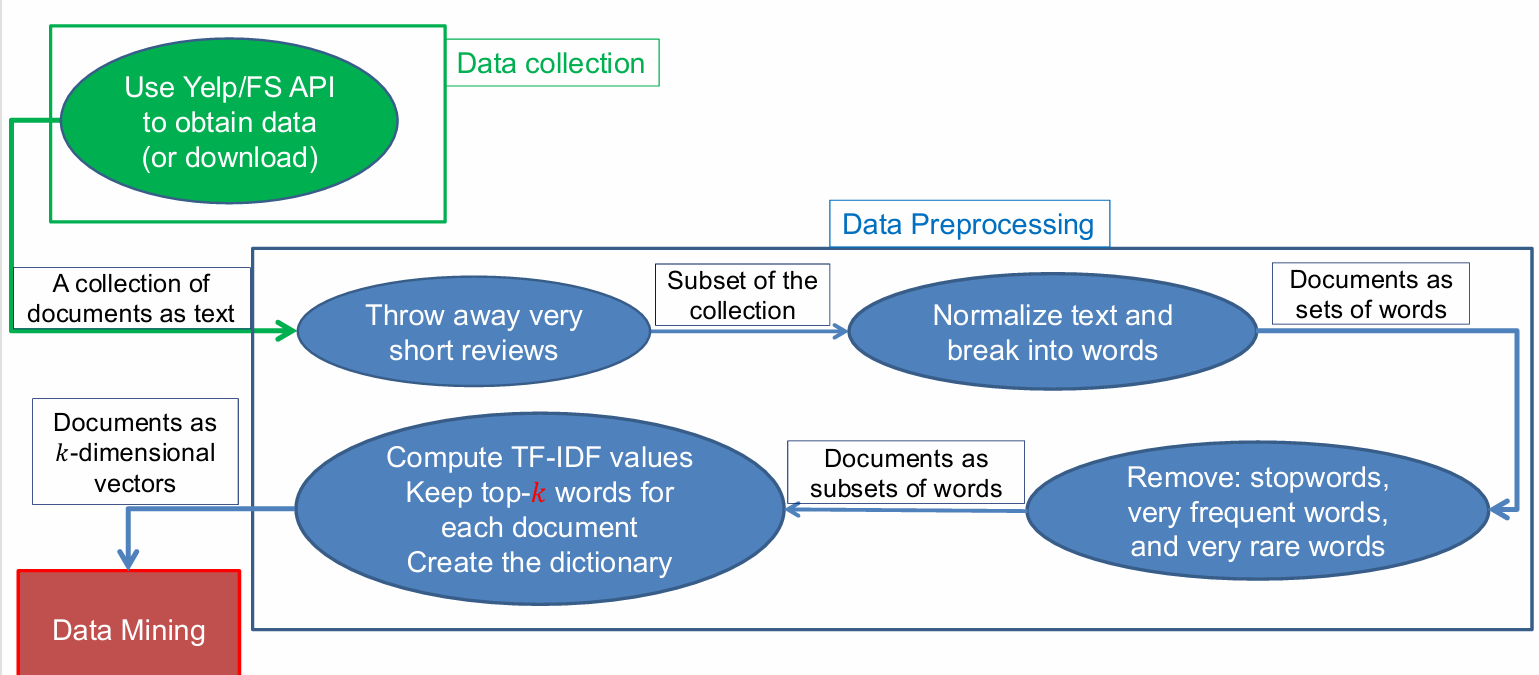
1. 数据收集（Data collection）：使用的API（应用程序编程接口）或文件系统（FS）来获取数据，或者直接下载数据。
2. 数据预处理（Data Preprocessing）：
   丢弃非常短的评论（Throw away very short reviews）：移除那些内容过少的评论，因为它们可能不包含足够的信息。
   文本规范化和分词（Normalize text and break into words）：将文本转换为统一的格式（如小写），去除标点符号和多余的空格，然后将文本分割成单词。
   文档作为单词集合（Documents as sets of words）：将每个文档表示为单词的集合。
   移除停用词、非常常见的词和非常罕见的词（Remove: stopwords, very frequent words, and very rare words）：去除那些对分析没有太大帮助的词，如停用词、过于常见或过于罕见的词。
   计算TF-IDF值（Compute TF-IDF values）：为每个文档计算TF-IDF值，这是一种衡量词语重要性的方法。
   保留每个文档的前k个词（Keep top-k words for each document）：选择每个文档中最重要的k个词。
   创建词典（Create the dictionary）：建立一个包含所有文档中独特词语的词典。
3. 数据挖掘（Data Mining）。

2.2.3.1.3 词嵌入（Word Embeddings）

TF-IDF是一种传统的文本表示方法，在文本挖掘中有着悠久的历史。

最近的趋势是使用词嵌入来表示文本。词嵌入是将每个单词映射到一个多维向量空间中。

这种方法利用了上下文的概念，即一个单词周围的单词。相似的单词往往出现在相似的上下文中。

因此，相似的单词应该被映射到彼此接近的向量位置。

以单词"movie"和"film"为例，这两个单词在语义上是相似的，并且很可能与相似的单词一起出现。

例如，它们都可能与"director"（导演）、"actor"（演员）、"actress"（女演员）、"scenario"（情节）、"script"（剧本）、"Oscar"（奥斯卡）和"cinemas"（电影院）等单词一起使用，所以这些相似的单词会被映射到向量空间中彼此接近的位置。

word2vec模型有两种方法用于生成词嵌入：

1. CBOW（Continuous Bag of Words）：

   CBOW模型的目标是学习单词的嵌入，以便给定上下文可以预测缺失的单词。

   在CBOW模型中，输入层是上下文中的单词，输出层是目标单词。

   模型通过学习权重矩阵来预测给定上下文中的目标单词。
   

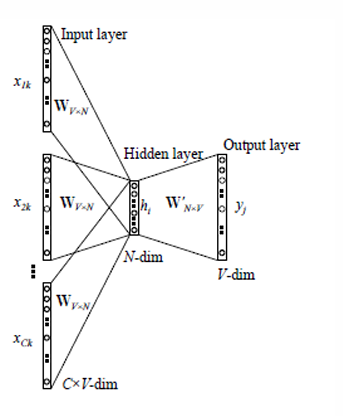
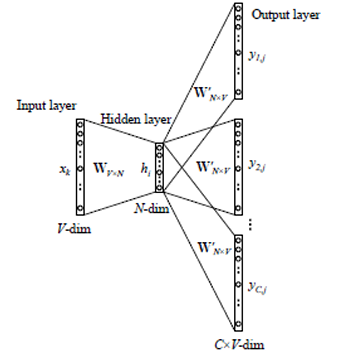
2. Skip-Gram：

   Skip-Gram模型的目标是学习单词的嵌入，以便给定一个单词可以预测其上下文。

   在Skip-Gram模型中，输入层是目标单词，输出层是上下文中的单词。

   模型通过学习权重矩阵来预测给定单词的上下文。
   

2.2.4 数据规范化

除了刚刚说的三个步骤以外，数据预处理可能还有数据规范化。

在许多情况下，使用规范化后的数据比使用原始值更为重要。数据规范化是将数据转换到一个特定的范围或分布，以便于比较和分析。

我们选择哪种数据规范化方法取决于我们想要达到的目标。不同的规范化方法适用于不同的场景和需求。

2.2.4.1 列规范化（Column Normalization）

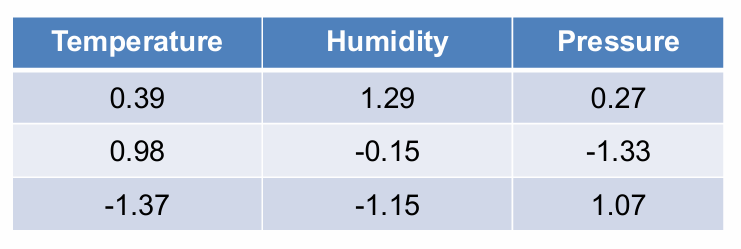
在数据集中，不同的特征可能具有非常不同的数值范围。例如，温度可能在0到100之间，而湿度可能在0到1之间，压力可能在0到几百之间。

当使用距离或相似性度量（如欧氏距离）来比较数据点时，具有较大数值范围的特征会对结果产生较大影响，导致具有较小数值范围的特征的影响被"淹没"或忽略。

为了使不同特征的影响在距离或相似性计算中可比较，需要对数据进行规范化处理，使它们具有相同的尺度。

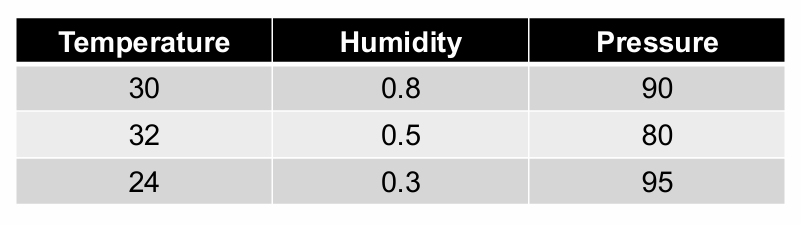
因此我们将每个特征列的值除以该列的最大值。这样，每个特征列的最大值将被缩放到1，而其他值将相应地缩放到0到1之间的范围。

规范化后，所有特征值都将落在[0, 1]的范围内，其中最大值为1。这使得不同特征的值可以直接比较，而不受原始数值范围的影响。

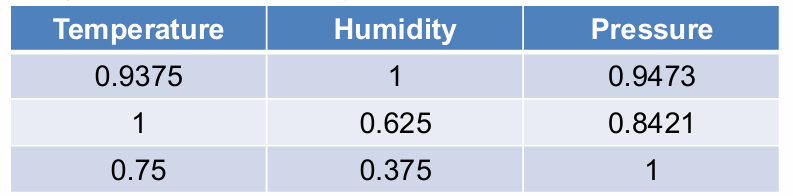
所以规范化公式：新值 = 旧值 / 列中的最大值。

2.2.4.1.1 特征中心化（Centering of features）

我们介绍另一种方法------特征中心化它有助于消除不同特征之间的量纲差异，使得数据更适合进行距离计算或相似性度量。

经过特征中心化处理后，每个特征列的平均值将变为零。这有助于提高某些机器学习算法的性能，如支持向量机（SVM）和主成分分析（PCA）。

中心化公式：新值 = 旧值 - 列的平均值。

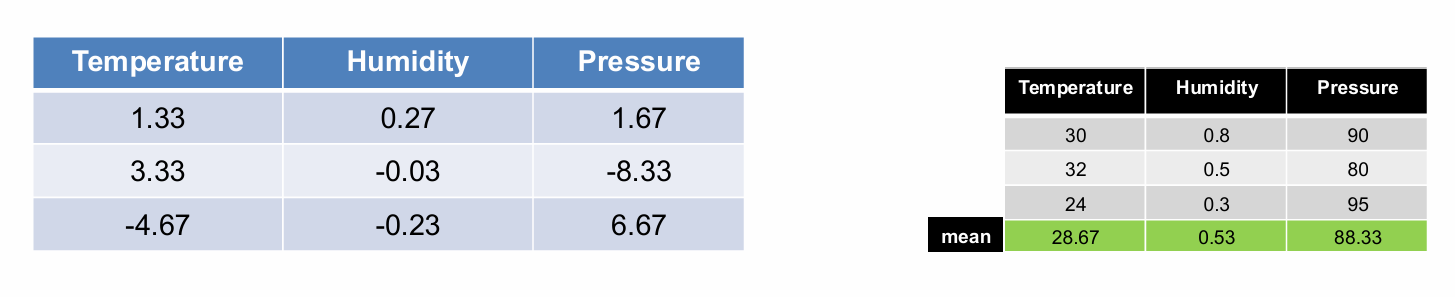
然后，将中心化后的数据除以其中心化列向量的长度（即欧氏范数），使得所有列成为单位向量（长度为1）。

这里标准化公式为：新值 = (旧值 - 均值) / √(旧值 - 均值)²的总和。

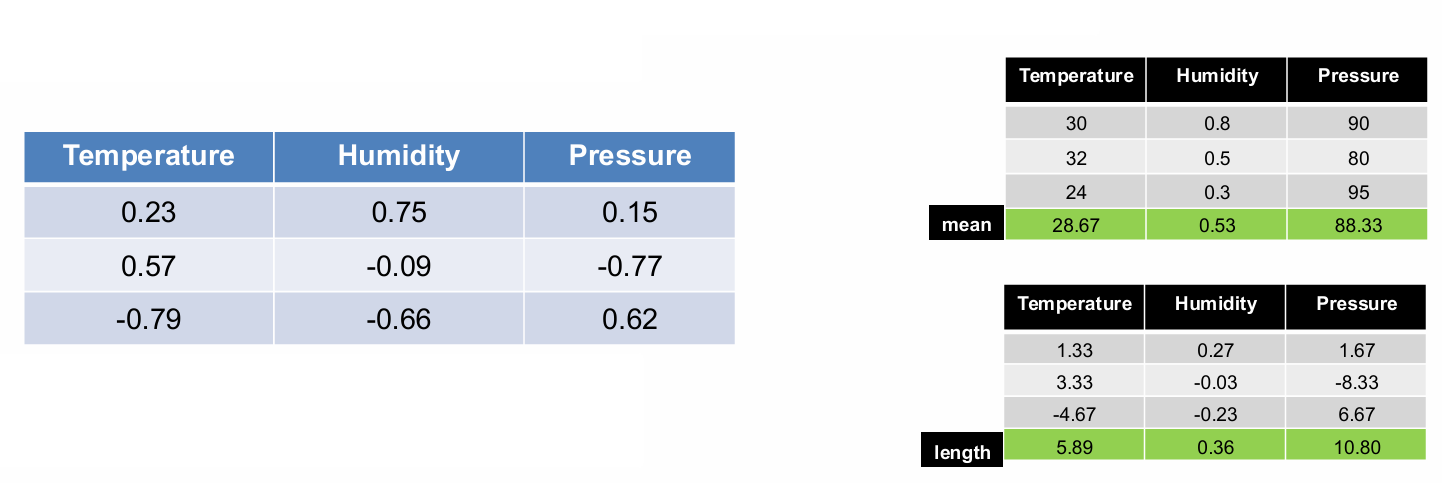
2.2.4.1.2 Z得分规范化（Z-score normalization）

这种方法通过将数据转换为标准正态分布（均值为0，标准差为1），使得不同特征具有可比性。

这个方法的第一步还是特征中心化，从每个特征列中减去其均值，使得所有列的均值变为零。

然后将中心化后的数据除以该特征列的标准差，使得数据符合标准正态分布。

这里标准化公式为：新值 = (旧值 - 均值) / 标准差。

细节如下： mean ( x ) = 1 N ∑ j = 1 N x j \text{mean}(x) = \frac{1}{N} \sum_{j=1}^{N} x_j mean(x)=N1∑j=1Nxj
std ( x ) = 1 N ∑ j = 1 N ( x j − mean ( x ) ) 2 \text{std}(x) = \sqrt{\frac{1}{N} \sum_{j=1}^{N} (x_j - \text{mean}(x))^2} std(x)=N1∑j=1N(xj−mean(x))2
z i = x i − mean ( x ) std ( x ) z_i = \frac{x_i - \text{mean}(x)}{\text{std}(x)} zi=std(x)xi−mean(x)

2.2.4.2 行规范化（Row Normalization）

我们现在尝试研究两个文档是否类似。

处理方法和前面类似，我们可以先尝试将其所有元素的值除以该行元素值的总和。

公式为新值 = 旧值 / 行中旧值的总和。

2.2.4.2.1 特征中心化（Centering of features）

我们再看一个例子分析两个用户是否以相似的方式对电影进行评分。

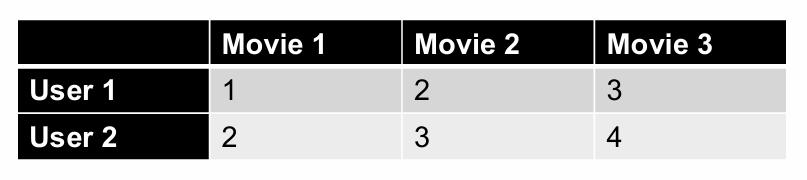
做法同样，从每个用户（行）的评分中减去该用户的平均评分，以使每行的平均值为零。

中心化公式：新值 = 旧值 - 列的平均值。

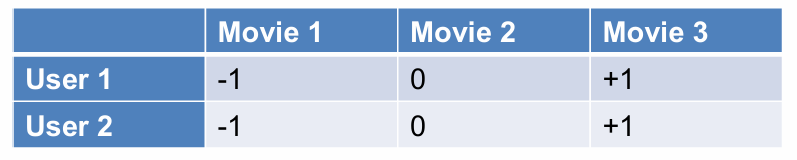
2.2.4.2.2 Z得分规范化（Z-score normalization）

类似地，Z得分衡量的是数据点距离均值的标准差数，它告诉我们一个数据点相对于平均值有多少个标准差。

这里标准化公式为：新值 = (旧值 - 均值) / 标准差。

细节如下： mean ( x ) = 1 N ∑ j = 1 N x j \text{mean}(x) = \frac{1}{N} \sum_{j=1}^{N} x_j mean(x)=N1∑j=1Nxj
std ( x ) = 1 N ∑ j = 1 N ( x j − mean ( x ) ) 2 \text{std}(x) = \sqrt{\frac{1}{N} \sum_{j=1}^{N} (x_j - \text{mean}(x))^2} std(x)=N1∑j=1N(xj−mean(x))2
z i = x i − mean ( x ) std ( x ) z_i = \frac{x_i - \text{mean}(x)}{\text{std}(x)} zi=std(x)xi−mean(x)

2.2.4.2.3 Softmax函数

现在我们有一个数据集反映了用户对各饭店的评分，我们想知道用户在三个餐厅中选择其中一个的概率。

Softmax函数用于将原始分数（或称为logits）转换为概率分布，同时确保这些概率的总和为1。

Softmax函数的公式为 Softmax ( x i ) = e x i ∑ j e x j \text{Softmax}(x_i) = \frac{e^{x_i}}{\sum_{j} e^{x_j}} Softmax(xi)=∑jexjexi.

2.2.4.2.4 逻辑函数（Logistic function）

如果我们想要将分数转换成用户再次访问餐厅的概率，应该如何处理？

这种转换与用户在三个餐厅中选择一个的概率是不同的。它实际上是关于用户再次访问或不访问某个餐厅的事件的概率分布。

其中一个思路是每个用户的评分都会被除以该用户的最大评分，从而将所有评分转换到0和1之间。

但这样处理规范化后的概率值中可能会出现1，这在实际中可能过于强烈，因为这意味着用户100%确定会再次访问某个餐厅，这在现实中通常不太可能。

我们可以使用另一种方法，逻辑函数。

逻辑函数是一种将实数映射到[0, 1]区间的函数，它模仿了阶跃函数（step function）的行为，是S型函数（sigmoid functions）的一种。

它模仿了阶跃函数，即当输入值足够大时，输出接近1；当输入值足够小时，输出接近0。
ϕ ( z ) = 1 1 + e − z \phi(z) = \frac{1}{1 + e^{-z}} ϕ(z)=1+e−z1

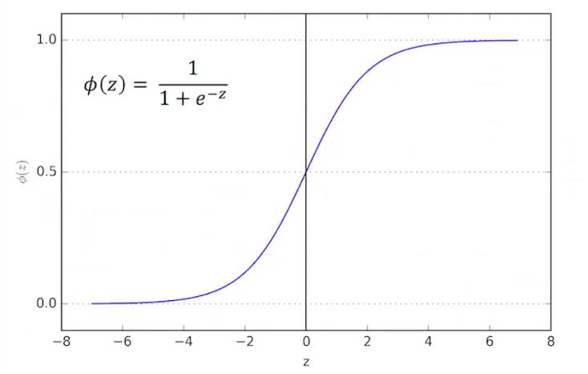
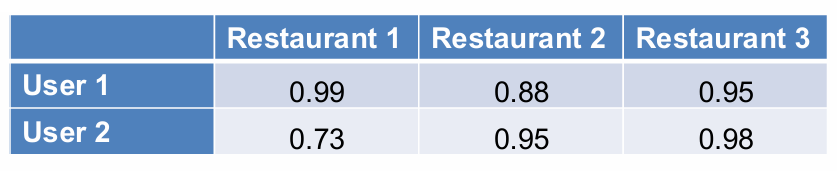
但我们发现得出的结果评分值都太大。

我们可以先进行均值中心化，对于每个特征（列），从每个数据点减去该特征的均值。

再应用逻辑函数将数据点转换为介于0和1之间的概率值。

2.2.4.2.5 激活函数（Sigmoid function）

S型函数是一种常用的激活函数，特别是在神经网络中，用于将输入值映射到0和1之间的概率值。

我们可以通过调整参数来控制函数的零点（zero point）和斜率（slope）。
f ( x ) = 1 1 + e − c 1 ⋅ ( x − c 2 ) f(x) = \frac{1}{1 + e^{-c_1 \cdot (x - c_2)}} f(x)=1+e−c1⋅(x−c2)1
c 1 c_1 c1控制函数的斜率，即函数在零点附近的陡峭程度。 c 1 c_1 c1值越大，函数越接近阶跃函数（step function）。
c 2 c_2 c2控制函数的中点，即函数输出0.5（或50%概率）的点。改变 c 2 c_2 c2会移动函数的中点，但不改变斜率。

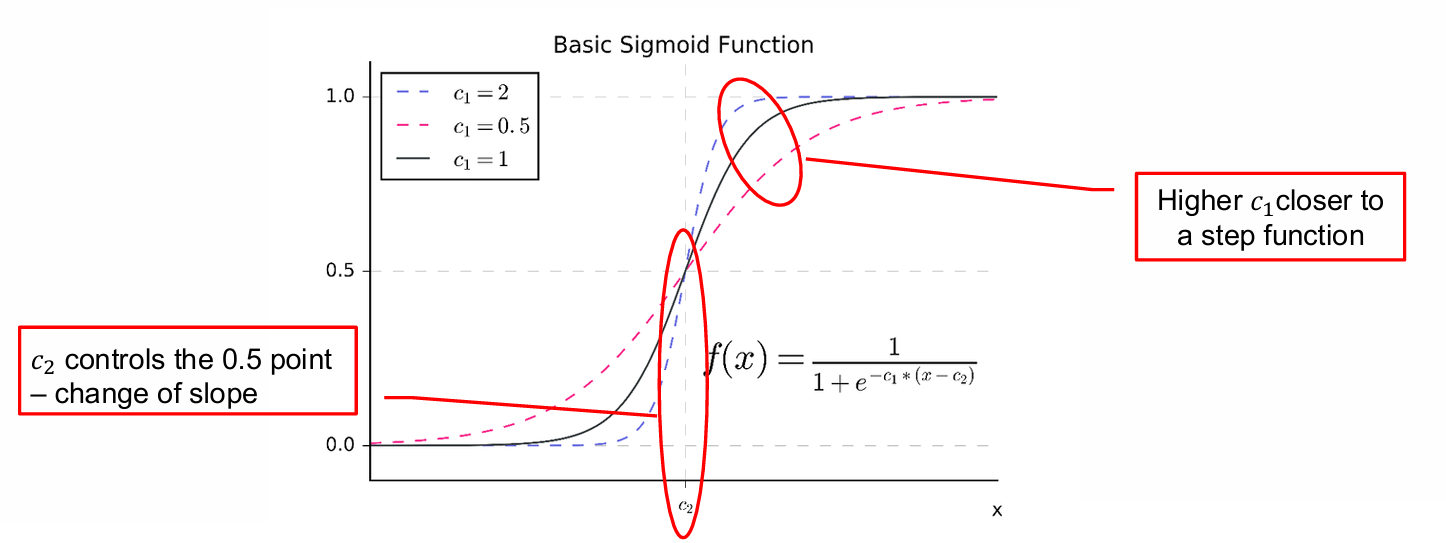
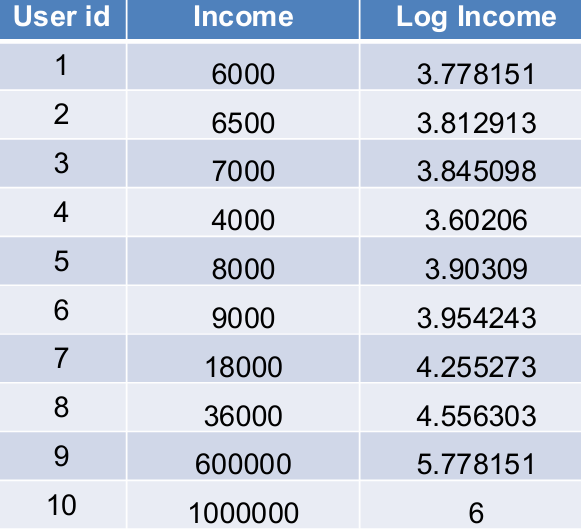
2.2.4.2.6 对数函数（Logarithm function）

当数据中的某些行或列的数值范围非常广泛时，直接规范化可能会使得较小的值在分析中被忽略或"淹没"。

在这种情况下，使用对数函数可以压缩数值范围，使得较小的值在分析中不会被忽略。

对数函数的公式为 l o g ( x ) log(x) log(x)。

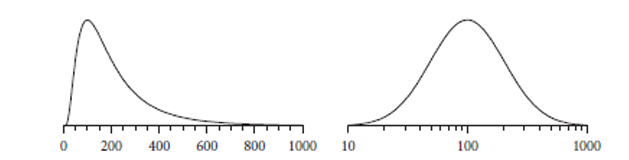
左图显示了原始的对数分布，右图显示了当所有值都转换为对数后的分布，看起来更接近高斯分布（Gaussian）。

因此前面的数据使用对数函数后结果如下图所示。

2.2.5 数据预处理的建议

原始数据通常很难收集，因此非常宝贵。建议保留原始数据的副本，以便在需要时可以回溯并更改处理步骤。

在数据处理流程中，保留每个中间步骤的输出是有用的。这有助于在流程的不同点进行小的更改，而不必每次都从头开始。

我们需要仔细记录预处理步骤，例如，如果丢弃非英语的评论，你可能会对数据集产生偏见。这种偏见应该被记录下来，因为它可能会影响分析结果的有效性。

2.3 数据后处理（Post-Processing）

后处理是指在数据收集、清洗和分析之后，对数据进行的进一步处理，使其对用户来说是可操作的和有用的。

这一步的目标是确保处理后的数据能够为用户带来实际价值，比如提供洞察、决策支持或直接的行动指导。

这一步涉及对分析结果进行统计检验，以评估结果的显著性和可靠性，还涉及数据可视化，将数据和分析结果以图形或图表的形式展现出来，使得数据更容易被理解和解释。

2.3.1 数据可视化（Visualization）

数据可视化是将数据转换成图形或图表的过程，目的是更直观地展示数据。

如果数据可视化得当，可以帮助我们直接用肉眼发现数据中的模式和展示趋势。

可视化的目的是以一种方式呈现数据，使得其中的模式可以被看到。

它的技术多种多样，我们下一章会进行介绍。

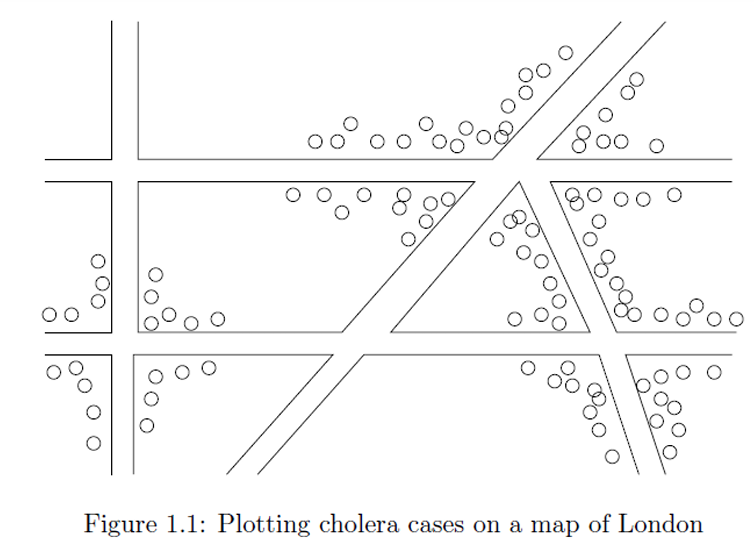
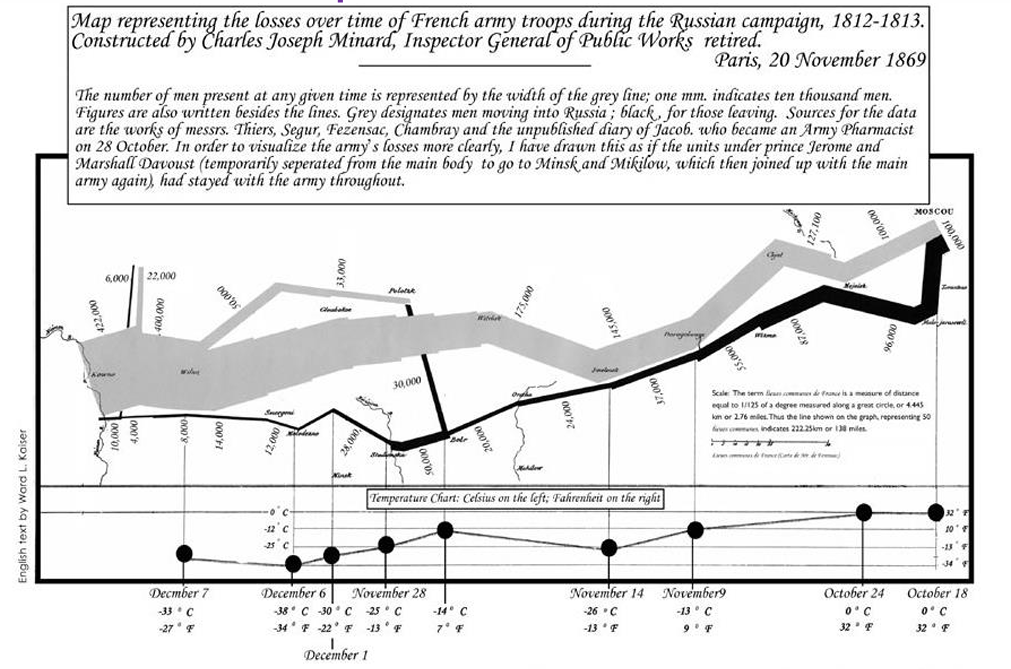
再比如一个大家可能经常用的例子是使用词云展示文本数据中词语的频率或重要性。

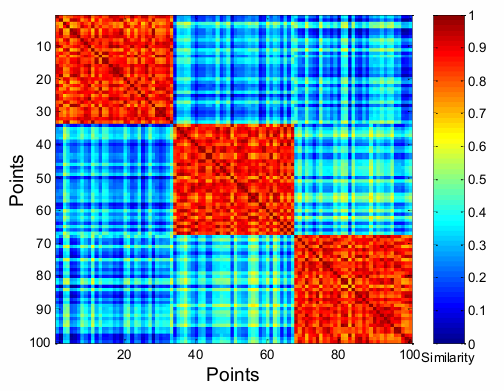
再比如使用热图（Heatmaps）展示点对点相似性矩阵（point-to-point similarity matrix）。

热图可以清晰地展示数据的聚类结构，即数据点如何分组。在热图中，相似的点（即属于同一聚类的点）会聚集在一起显示为相同的颜色块。

还可用于别的地方，如下图所示。

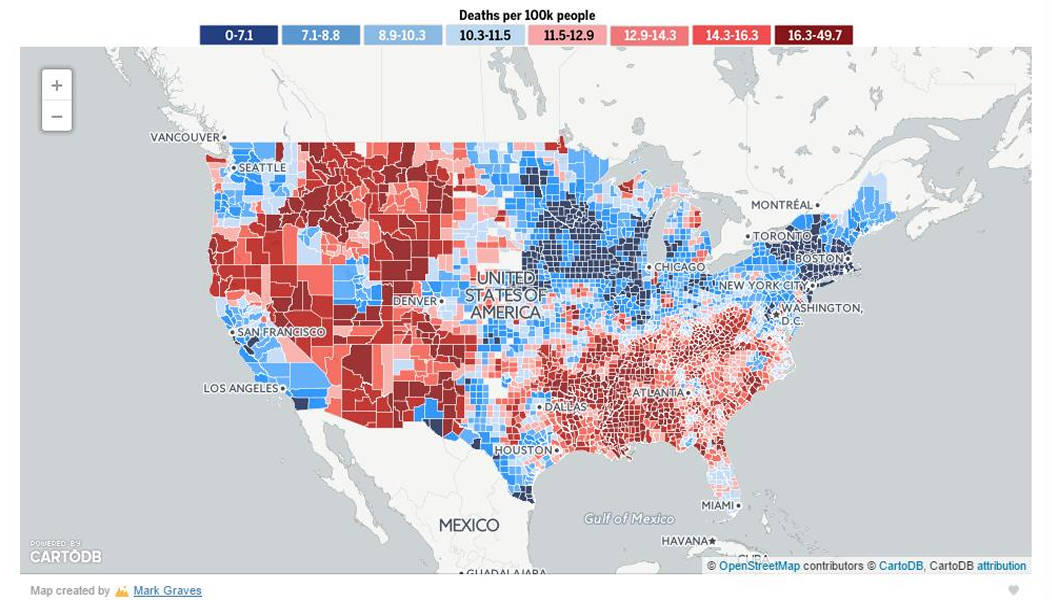
因此我们这里可能还会使用到降维操作。

因为人眼在视觉上最多只能有效地处理二维（2D）或最多三维（3D）的可视化。对于更高维度的数据，我们很难直观地理解和解释。

它将高维数据转换到低维空间，通常是二维，以便进行可视化。这使得我们可以在二维平面上展示和分析原本高维的数据。

距离保持嵌入（distance preserving embeddings）也是一种将高维数据映射到低维空间的方法。

常见的距离保持嵌入技术包括主成分分析（PCA）、t-分布随机邻（t-SNE）和统一流形嵌入（UMAP）等。

这些都可以帮助我们更好进行数据可视化。

2.3.1.1 非线性降维（Non-linear dimensionality reduction）

非线性降维是指使用非线性变换将高维数据映射到低维空间的技术，以便更好地进行可视化和分析。

传统的降维方法，如主成分分析（PCA），通常使用线性变换来改变坐标轴。这些方法可能不足以捕捉数据的复杂结构。

非线性技术能够更好地处理复杂的数据结构，提供更优的可视化效果。

t-SNE技术正是一种非线性降维技术。

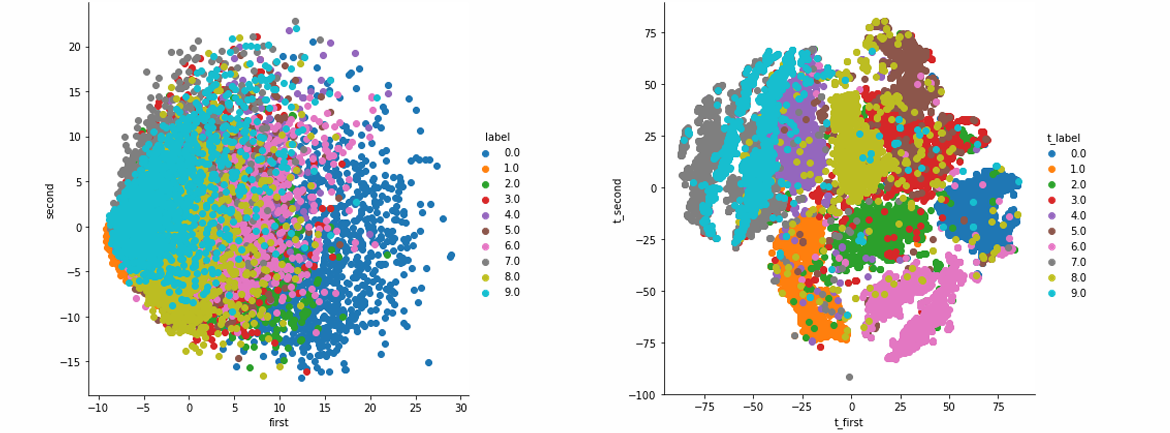
左侧图展示了使用传统方法（可能是PCA）的降维结果，右侧图展示了使用t-SNE方法的结果。

在t-SNE图中，不同类别的数据点（不同颜色表示不同类别）形成了更清晰的聚类，显示了t-SNE在保持数据局部结构方面的优势。

2.3.2 统计显著性（Statistical Significance）

当我们从大型数据集中提取知识时，需要确保我们的发现不是随机性的副产品。统计显著性帮助我们确定观察到的模式或关系是否具有统计学意义。

例如，如果我们发现许多人同时购买牛奶和卫生纸，这可能表明存在某种关联。

但是，如果更多的人分别独立购买牛奶和卫生纸，那么这种关联可能不那么显著。

统计检验将实验结果与由零假设（null hypothesis）生成的结果进行比较。

零假设通常是一个假设，例如，人们独立选择商品。

如果结果不能通过随机性产生，那么它就是有趣的，值得进一步研究。

正确定义零假设是一个重要问题。零假设应该反映"随机性"的情况，即在没有实际关联或效应的情况下会发生什么。

2.3.3 没有实际意义的发现

在数据分析中，我们可能会"发现"一些实际上没有意义的模式。

这里介绍两个理论：

1. 邦费罗尼原理（Bonferroni's principle）：
   如果你在比数据所能支持的更多地方寻找有趣的模式，那么你一定会发现一些没有意义的结果。
2. 莱茵悖论（The Rhine Paradox）：
   如果研究者在实验中不断调整假设或方法，直到找到他们想要的结果，那么他们最终找到的"结果"可能只是偶然的产物，而不是真实的科学发现。

因此我们要小心过度拟合（overfitting），它所带来的结果往往是无意义的。

我们回到莱茵悖论，这个悖论的实验过程如下：

约瑟夫·莱茵（Joseph Rhine）假设某些人拥有超感官知觉（Extra-Sensory Perception，简称ESP）的能力。

在这个实验中，参与者被要求猜测10张隐藏的卡片的颜色------红色或蓝色。

莱茵发现，几乎每1000人中就有1人表现出ESP能力------他们能够猜对所有10张卡片的颜色。

莱茵告诉那些在第一次测试中表现出ESP（超感官知觉）能力的参与者，他们确实拥有这种能力，并邀请他们参加另一次相同类型的测试。

在第二次测试中，莱茵发现几乎所有这些参与者都失去了他们的ESP能力。

莱茵得出的结论是，不应该告诉人们他们拥有ESP能力，因为这会导致他们失去这种能力。

这里无论是第一次发现ESP能力，还是后面得到的不能告诉人们有ESP能力都是错误的结论，没有实际意义，我们应该避免得到这样的发现。