算法24.0 - 技术栈

153. 寻找旋转排序数组中的最小值 - 力扣（LeetCode）

自己的理解：

如果题目表现出来明显的二段性可以考虑用二分算法

为什么C--D $i$ <=nums $n-1$ ？

因为c--d里面的元素有可能包含着d 所以是小于等于

还有没有别的二段性？

AB段的元素都比A大 CD段的元素都比A小选择A点的值作为参照物

这个时候需要边界情况的考虑如果旋转之后是一个完整递增的数组(和原数组一样)

为什么当以A点为划分二段性是出现这样的错误if(nums $mid$ >=x) left=mid+1; //right = mid ;？

认真画图就可以知道问题出在哪里

细节：

审题要认真审题题目有些关键词是思路的提示(例如时间复杂度例这道题里面的nums中所有整数互不相同)

二分算法画图的时候要和题目信息相关

例如这道题 left和right的中间点mid 落到的是AB和CD里面这样找就容易找到二分算法的条件

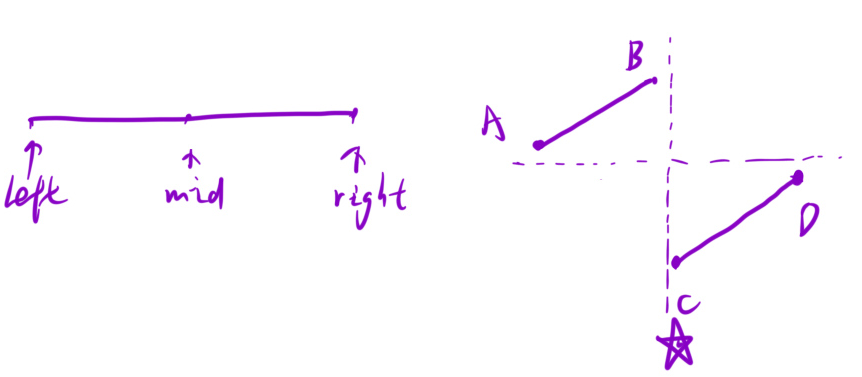
别人的讲解：

暴力解法：遍历一遍数组然后找到结果

优化暴力解法：

A--B C--D 这是明显的二段性考虑用二分查找

这里的二段性是：AB中的元素大于D CD里面的元素小于D

A--B nums $i$ >nums $n-1$ C--D $i$ <=nums $n-1$

开始二分查找如果mid落在了ab上 mid小于ret 那么下一步是left=mid+1 （可以绕过去因为ab里面并没有d）

如果mid落在了cd上 mid>ret 那么下一步是right=mid (right不可以绕过去因为有可能跳过要查找的元素)

下面是思路图：

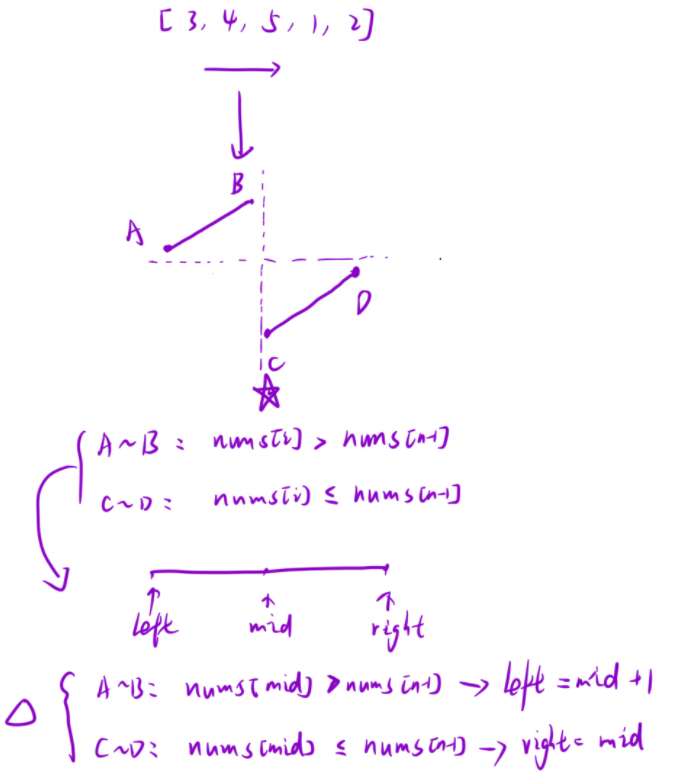
下面是题目、效果图和代码：

java 复制代码

class Solution 
{
    //选择A点为参照物
    public int findMin(int[] nums) 
    {  
        int left = 0 ,right = nums.length-1;
        int x = nums[left] ;//记录下A点的元素
        
        //特殊情况的处理
        if(nums[left]<nums[right])
        {
           return nums[left];
        }


        while(left<right)
        {
            int mid = left+(right-left)/2;
            
            if(nums[mid]>=x) left=mid+1; //right = mid ;
            else right = mid ;//left = mid + 1;
        }
        return nums[left];
    }
}
//特殊情况的处理：如果旋转一个循环呢  到时候结果是原数组

java 复制代码

class Solution 
{
    public int findMin(int[] nums) 
    {
       int left = 0,right = nums.length-1;
       int x =nums[right];//标记一下最后元素的位置 也就是思路图里面的D元素
       while(left<right)
       {
        int mid = left + (right-left)/2;
        if(nums[mid]>x) left = mid + 1;
        else right = mid ; 
       }
       return nums[left];
    }
}
//xiyu251103&1#3*6