一、核心概述
Scaled Dot-Product Attention(缩放点积注意力)的核心步骤------注意力分数计算,基于C++标准库实现,核心公式为:
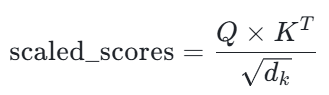
其中Q(查询矩阵)、K(键矩阵)均为4×512维度,是K的转置矩阵,
为特征维度,缩放操作可避免高维度数值过大影响后续计算。代码全程使用
std::vector<std::vector<double>> 实现矩阵操作,聚焦核心逻辑。
以下为手动计算过程和结果:

二、完整代码
#include <iostream>
#include <vector>
#include <cmath>
#include <iomanip> // 用于控制输出精度
// 定义矩阵类型:二维double向量
using Matrix = std::vector<std::vector<double>>;
/**
* @brief 矩阵转置
* @param mat 输入矩阵(m×n)
* @return 转置后的矩阵(n×m)
*/
Matrix transpose(const Matrix& mat) {
if (mat.empty() || mat[0].empty()) return {};
int rows = mat.size();
int cols = mat[0].size();
Matrix transposed(cols, std::vector<double>(rows));
for (int i = 0; i < rows; ++i) {
for (int j = 0; j < cols; ++j) {
transposed[j][i] = mat[i][j];
}
}
return transposed;
}
/**
* @brief 矩阵乘法(仅支持 m×n × n×p → m×p)
* @param A 矩阵A(m×n)
* @param B 矩阵B(n×p)
* @return 乘积矩阵C(m×p)
*/
Matrix matrixMultiply(const Matrix& A, const Matrix& B) {
if (A.empty() || B.empty() || A[0].size() != B.size()) {
throw std::invalid_argument("矩阵维度不匹配,无法相乘");
}
int m = A.size(); // A的行数
int n = B.size(); // B的行数 = A的列数
int p = B[0].size(); // B的列数
Matrix result(m, std::vector<double>(p, 0.0));
// 三重循环实现矩阵乘法
for (int i = 0; i < m; ++i) {
for (int j = 0; j < p; ++j) {
for (int k = 0; k < n; ++k) {
result[i][j] += A[i][k] * B[k][j];
}
}
}
return result;
}
/**
* @brief 计算Scaled Dot-Product Attention分数(Q*K^T / sqrt(d_k))
* @param Q 查询矩阵(4×512)
* @param K 键矩阵(4×512)
* @param d_k K的特征维度(这里固定为512)
* @return 缩放后的注意力分数矩阵(4×4)
*/
Matrix computeScaledAttentionScores(const Matrix& Q, const Matrix& K, int d_k = 512) {
// 计算K的转置
Matrix K_T = transpose(K);
// 计算Q * K^T
Matrix QK_T = matrixMultiply(Q, K_T);
// 缩放:除以sqrt(d_k)
double scale = std::sqrt(d_k);
Matrix scaledScores(QK_T.size(), std::vector<double>(QK_T[0].size(), 0.0));
for (int i = 0; i < QK_T.size(); ++i) {
for (int j = 0; j < QK_T[0].size(); ++j) {
scaledScores[i][j] = QK_T[i][j] / scale;
}
}
return scaledScores;
}
int main() {
try {
int rows = 4;
int cols = 512;
Matrix Q(rows, std::vector<double>(cols, 0.0));
Matrix K(rows, std::vector<double>(cols, 0.0));
Q[0][0] = 1.0; Q[0][1] = 2.0;
Q[1][0] = 3.0; Q[1][1] = 4.0;
K[0][0] = 5.0; K[0][1] = 6.0;
K[1][0] = 7.0; K[1][1] = 8.0;
// 计算缩放后的注意力分数
Matrix scaledScores = computeScaledAttentionScores(Q, K);
// 输出结果
std::cout << "缩放后的注意力分数矩阵(前2行前2列):" << std::endl;
std::cout << std::fixed << std::setprecision(8);
for (int i = 0; i < 2; ++i) {
for (int j = 0; j < 2; ++j) {
std::cout << "scores[" << i << "][" << j << "] = " << scaledScores[i][j] << std::endl;
}
}
}
catch (const std::exception& e) {
std::cerr << "错误:" << e.what() << std::endl;
return 1;
}
return 0;
}三、核心代码逻辑拆解
3.1 整体流程
代码核心是按公式分步实现,先完成矩阵转置、矩阵乘法,再执行缩放操作,最终得到注意力分数矩阵(4×4维度)。
3.2 关键函数逻辑
3.2.1 矩阵转置
核心作用:将K矩阵(4×512)转为K^T(512×4),满足Q×K^T的矩阵乘法维度要求(Q为4×512,仅能与512行的矩阵相乘)。通过双重循环交换元素位置,实现转置。
3.2.2 矩阵乘法
核心作用:计算Q与K^T的乘积,得到4×4的原始注意力分数矩阵。先校验维度合法性(A的列数需等于B的行数),再通过三重循环累加计算乘积,确保结果维度正确(4×4)。
3.2.3 注意力分数计算
核心步骤(按顺序):
-
调用transpose函数,得到K矩阵的转置K^T;
-
调用matrixMultiply函数,计算Q与K^T的乘积QK_T(4×4);
-
计算缩放因子(d_k=512),用于缓解高维度数值偏差;
-
将QK_T的每个元素除以缩放因子,得到最终的缩放注意力分数,返回结果。
3.2.4 主函数
核心作用:构造测试数据、调用核心函数、输出结果。初始化4×512的Q、K矩阵,仅给前2行前2列赋值(便于手动验证结果),调用核心函数计算分数后,输出前2行前2列的结果。同时添加异常捕获,处理维度不匹配等错误。
四、拓展
4.1 完整注意力机制补充
仅实现了"注意力分数计算",完整的Scaled Dot-Product Attention需两步后续操作:
-
Softmax归一化:对缩放后的注意力分数执行Softmax操作,将分数转化为0-1的注意力权重,确保权重之和为1,突出重要特征;
-
权重与V矩阵相乘:将注意力权重与V(Value,值矩阵,维度与Q/K一致)相乘,得到最终的注意力输出,完成特征筛选与融合。
4.2 性能优化方向
可从多维度优化计算性能:替换矩阵乘法实现方式,舍弃基础的三重循环,改用 Eigen、OpenBLAS 等专业线性代数库以大幅提升大规模矩阵计算效率;通过 const 引用传递矩阵减少不必要的 vector 拷贝操作,降低内存开销;利用 OpenMP 对矩阵乘法的三重循环做并行化处理,适配多核心 CPU 提升计算速度;精度层面可根据需求调整,替换为 long double 类型提升精度,或替换为 float 类型追求更快计算速度。