Abstract
从相机到屏幕,研究人员已开发出一套成熟的系统,用于捕捉和复现人眼的色彩感知体验。本研究旨在对这一流程进行升级,将传统的 RGB(红绿蓝)色彩复现转变为多光谱图像(MSI)色彩复现。尽管多光谱图像在色彩匹配方面具有显著优势,但研究发现,要充分利用更多光谱信息实现色彩恒常性并非易事。因此,我们提出了一套正则化色彩复现系统,该系统包含两个核心部分:一是基于光谱先验引导的优化策略,用于建立传感器优化的 RGB 投影以实现色彩匹配;二是基于学习的色适应模型,用于实现色彩恒常性。具体而言,我们在传感器光谱灵敏度的引导下,通过端到端优化来定义 RGB 投影。随后,我们设计了一个色适应神经网络,该网络分别实现两项功能:估算场景光照度,以及生成光照度自适应矩阵以完成自动白平衡和动态色彩校正。综合实验表明,与其他备选方案相比,我们的系统表现更具优越性。
Introduction
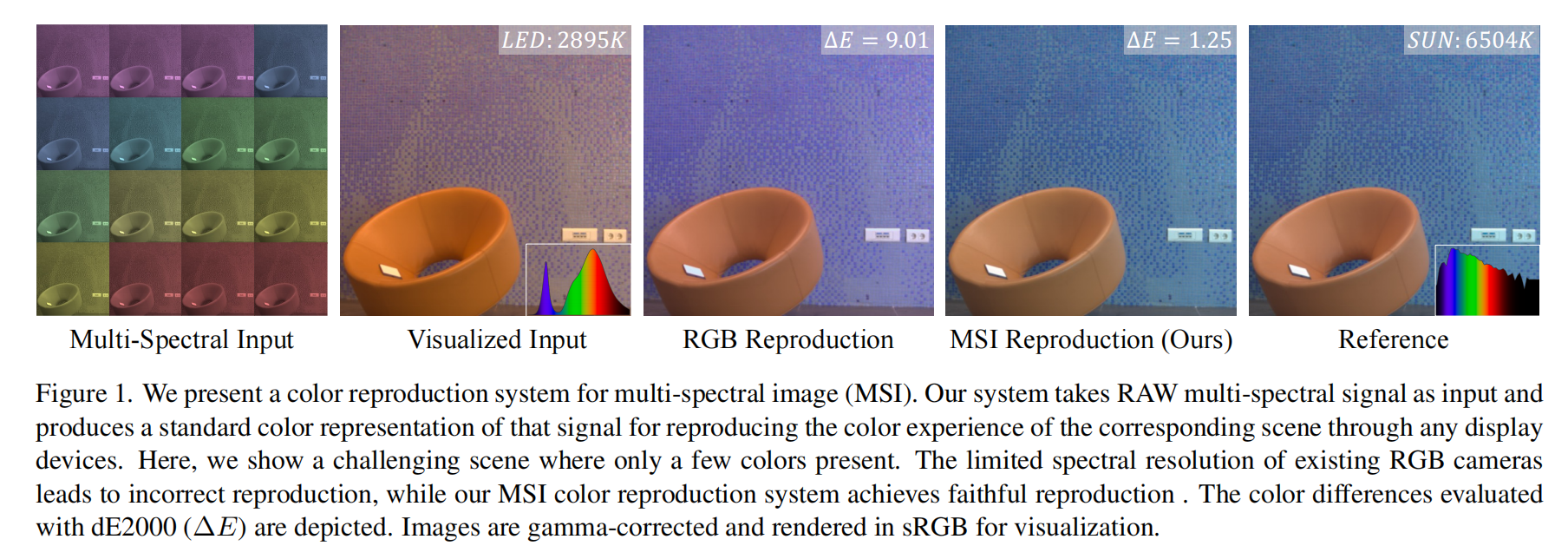
- 图 1 我们提出了一种用于多光谱图像(MSI)的色彩还原系统。该系统以原始多光谱信号作为输入,生成该信号的标准色彩表示,从而通过任意显示设备还原对应场景的色彩体验。在此,我们展示了一个仅含少量色彩的挑战性场景。现有 RGB 相机有限的光谱分辨率会导致色彩还原不准确,而我们的多光谱图像色彩还原系统能够实现真实还原。文中还呈现了通过 dE2000(ΔE)评估得出的色差值。所有图像均经过伽马校正,并以 sRGB 格式渲染,以便可视化呈现。
色彩复现的目标是精准捕捉并还原色彩,使其与人类眼睛感知到的原始色彩高度相似。对精准色彩复现的追求,在多个应用领域中都具有重要意义,例如印刷、数字成像、视频制作和电影行业。在这些领域中,保持色彩保真度是实现有效视觉传达的关键 [31,64,69]。
除了匹配人眼的色敏特性,精准复现色彩还需模拟人类通过色适应维持色彩恒常性的能力。
从显示端来看,为确保不同媒介间色彩复现的一致性,具有预定义白点(如 D65 标准光源)的设备无关色空间(如 CIE XYZ 色空间)与色域(如 sRGB 色域)已实现标准化,用于复现人类的色彩感知。
但从成像端来看,由于光照环境存在差异,将 RAW 格式信号转换为标准色彩表示面临诸多挑战。此外,成像设备本身(通常是 RGB 相机)的光谱分辨率有限,导致成像过程中会损失大量光谱信息,进而在复杂场景下产生色彩失真的结果,如图 1 所示。
本研究初步探索如何通过更高的光谱分辨率(即多光谱图像,MSI)实现精准色彩复现。与仅依赖三个光谱通道的传统 RGB 相机不同,多光谱相机能够捕捉更广泛的光谱数据,从而获取更精准、更详细的光谱信息 [17,45]。为了展示多光谱图像在色彩表示方面的优势,我们以色彩匹配为例:在标准光源下,构建线性投影矩阵,将多光谱图像 RAW 信号或 RGB 图像 RAW 信号投影到标准 CIE XYZ 色空间。图 2 所示结果表明,更高的光谱分辨率在精准匹配低维色空间方面具有明显优势。但另一方面,即便通过提高光谱分辨率,要实现色彩恒常性也并非易事 ------ 即便为每幅多光谱图像估算出场景自适应投影矩阵,这种直接投影的方式仍会导致色彩饱和度不足。
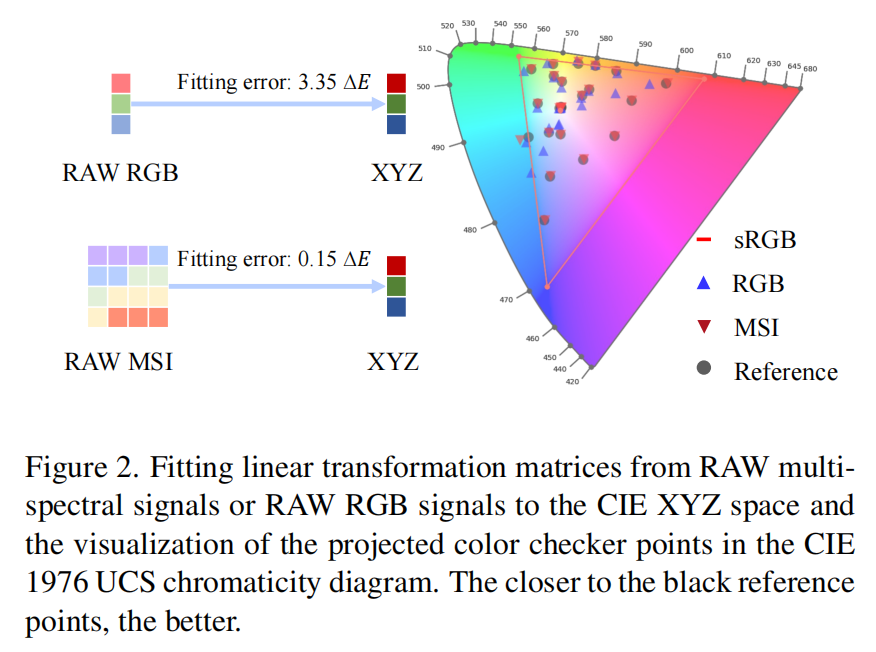
- 图 2 将原始多光谱信号或原始 RGB 信号的线性变换矩阵拟合到 CIE XYZ 空间,并在 CIE 1976 UCS 色度图中对投影后的色卡色点进行可视化呈现。色点越接近黑色参考点,效果越好。
因此,多光谱图像(MSI)色彩复现系统的核心,在于确定一种最优且可靠的转换方式 ------ 将多光谱信号映射到标准色空间,同时确保精准的色彩匹配与色彩恒常性。为实现这一目标,我们设计了一套正则化色彩处理流程。该流程包含两部分核心内容:一是基于光谱先验引导的优化策略,用于建立传感器优化的 RGB 投影以实现色彩匹配;二是基于学习的色适应模型,用于实现色彩恒常性。除了拟合标准 CIE XYZ 色空间外,我们还对色彩匹配原理进行了推广:在传感器光谱灵敏度的引导下,通过对色彩处理流程进行端到端优化,确定了一个适用于计算色彩恒常性的 RGB 子空间。
在确定的子空间中,我们通过引入色适应神经网络来实现色彩恒常性。该网络可完成两项任务:一是估算场景光照度,二是生成光照度自适应色彩校正矩阵,分别用于自动白平衡和动态色彩校正。
然而,获取训练这种基于学习的模型所需的多光谱数据,过程可能既耗时又昂贵。为解决这一问题,我们提出了一种多光谱数据增强策略,该策略以 "色彩 - 反射率检索字典" 为核心,能够从海量已有的高质量 sRGB 图像中生成高光谱反射率数据。因此,我们可以在大规模合成数据集上对模型进行预训练,进而提升模型的泛化能力,并增强其整体鲁棒性。
相机旨在模拟人类视觉系统的感知过程。在简化的朗伯体成像模型中,相机捕捉到的原始响应 I(x)\mathbf{I}(x)I(x) 可表示为:
I(x)=∫λe(λ)r(λ;x)sc(λ)dλ(1) \mathbf{I}(x) = \int_{\lambda} e(\lambda)r(\lambda; x)s_c(\lambda)d\lambda \tag{1}I(x)=∫λe(λ)r(λ;x)sc(λ)dλ(1)
在该公式中,像素位置 xxx 处的原始响应,是传感器光谱灵敏度 sc(λ)s_c(\lambda)sc(λ),物体光谱反射率 r(λ;x)r(\lambda; x)r(λ;x) 与场景光源光谱功率分布(SPD)e(λ)e(\lambda)e(λ) 三者积分的结果。积分过程针对每个光谱通道 ccc,在波长 λ\lambdaλ 的范围内进行。
该公式假设场景光源在不同像素位置上具有全局均匀性,并且我们将场景光源的传感器响应(称为场景光照度向量)定义为 L=∫λe(λ)sc(λ)dλ\mathbf{L} = \int_{\lambda} e(\lambda)s_c(\lambda)d\lambdaL=∫λe(λ)sc(λ)dλ。
色彩还原的核心目标,是将传感器特定信号映射为一种标准化的色彩表示,该表示需同时具备设备无关性与光照无关性。前者意味着采用类人眼的三通道 RGB 空间,即 CIE XYZ 空间,该空间源于色匹配实验 [33, 66]。后者则需要通过计算式色彩恒常性处理,将色彩校正为与显示设备参考光源(如 6504K 日光,即 D65 光源)下捕捉的色彩一致的效果。由于相机的 RAW 信号具有设备依赖性。实际应用中,制造商需在标准光源下,针对 ColorChecker(色卡)颜色校准出一个 3×3 色彩校正矩阵(如图 2 (a) 所示)。该固定色彩校正矩阵用于修正误差,最终在 CIE XYZ 空间中得到设备无关信号,以实现色彩匹配。随后,色彩处理流程中的自动白平衡算法,会为每个场景确定冯・克里茨(von Kries)形式对角矩阵的数值,得到光照无关信号,从而实现色彩恒常性。
IRGB=IRAW⋅MCC⋅MWB(2) \mathbf{I}{RGB} = \mathbf{I}{RAW} \cdot \mathbf{M}{CC} \cdot \mathbf{M}{WB} \tag{2} IRGB=IRAW⋅MCC⋅MWB(2)
- IRAW∈RH×W×3\mathbf{I}_{RAW} \in \mathbb{R}^{H \times W \times 3}IRAW∈RH×W×3 表示 RAW 图
- MCCM_{CC}MCC 表示色彩转换矩阵
- MWBM_{WB}MWB 表示白平衡系数矩阵
- IRGB∈RH×W×3\mathbf{I}_{RGB} \in \mathbb{R}^{H \times W \times 3}IRGB∈RH×W×3 表示颜色校正后的 RGB 图
在白平衡场景下(其目标是校正消色差颜色,即 R=G=B 的情况),色彩恒常性已得到广泛研究 [2, 4, 9, 12, 13, 18, 19, 25, 26, 36, 40, 43, 48]。统计方法会对不同物体的物体反射率做出假设,当这些假设不成立时,方法会产生较差的结果 [13, 25, 44, 61]。基于色域的方法也已被提出 [26, 30]。近年来,基于学习的模型通过利用带标注的数据对,展现出了良好的性能 [1, 7, 8, 8, 10, 22, 37, 46, 50, 56, 57, 67, 71, 72]。目前,针对消色差颜色之外的色彩恒常性研究也日益增多 [15,16,23],具体方式为再乘以一个 3×3 矩阵。尽管 RGB 相机的色彩恒常性研究已取得显著进展,但在多光谱图像(MSIs)场景下的相关研究仍较为有限 [14, 41, 42]。Chakrabarti 等人提出利用空谱统计信息,该思路与 RGB 色彩恒常性方法类似 [14]。Khan 等人则将统计方法扩展到了多光谱通道 [41]。Koskinen 等人专注于使用单像素多光谱传感器进行光照估计 [42]。其他研究还探索了多光谱图像中光照与反射率的分解 [47, 73]。Glatt 等人还发布了一个用移动设备采集的多光谱图像数据集,用于光照估计 [32]。上述方法仅解决了色彩再现任务的一部分(主要是色彩恒常性),与之不同的是,本文提出了一个完整的系统,可同时实现色彩匹配与色彩恒常性。
Multi-Spectral Image Color Reproduction
Regularized Color Pipeline
遵循标准 RGB 色彩再现的公式推导,多光谱图像的色彩再现任务可表述为:
IRGB=IMSI⋅T(3) \mathbf{I}{RGB} = \mathbf{I}{MSI} \cdot \mathbf{T} \tag{3} IRGB=IMSI⋅T(3)
其中,IMSI∈RH×W×C\boldsymbol{I}{\text{MSI}} \in \mathbb{R}^{H \times W \times C}IMSI∈RH×W×C 表示多光谱传感器的原始响应(RAW response),C 代表光谱通道数;IRGB∈RH×W×3\boldsymbol{I}{\text{RGB}} \in \mathbb{R}^{H \times W \times 3}IRGB∈RH×W×3 代表目标 RGB 图像;T\boldsymbol{T}T 则是一个 C×3C \times 3C×3 维矩阵。
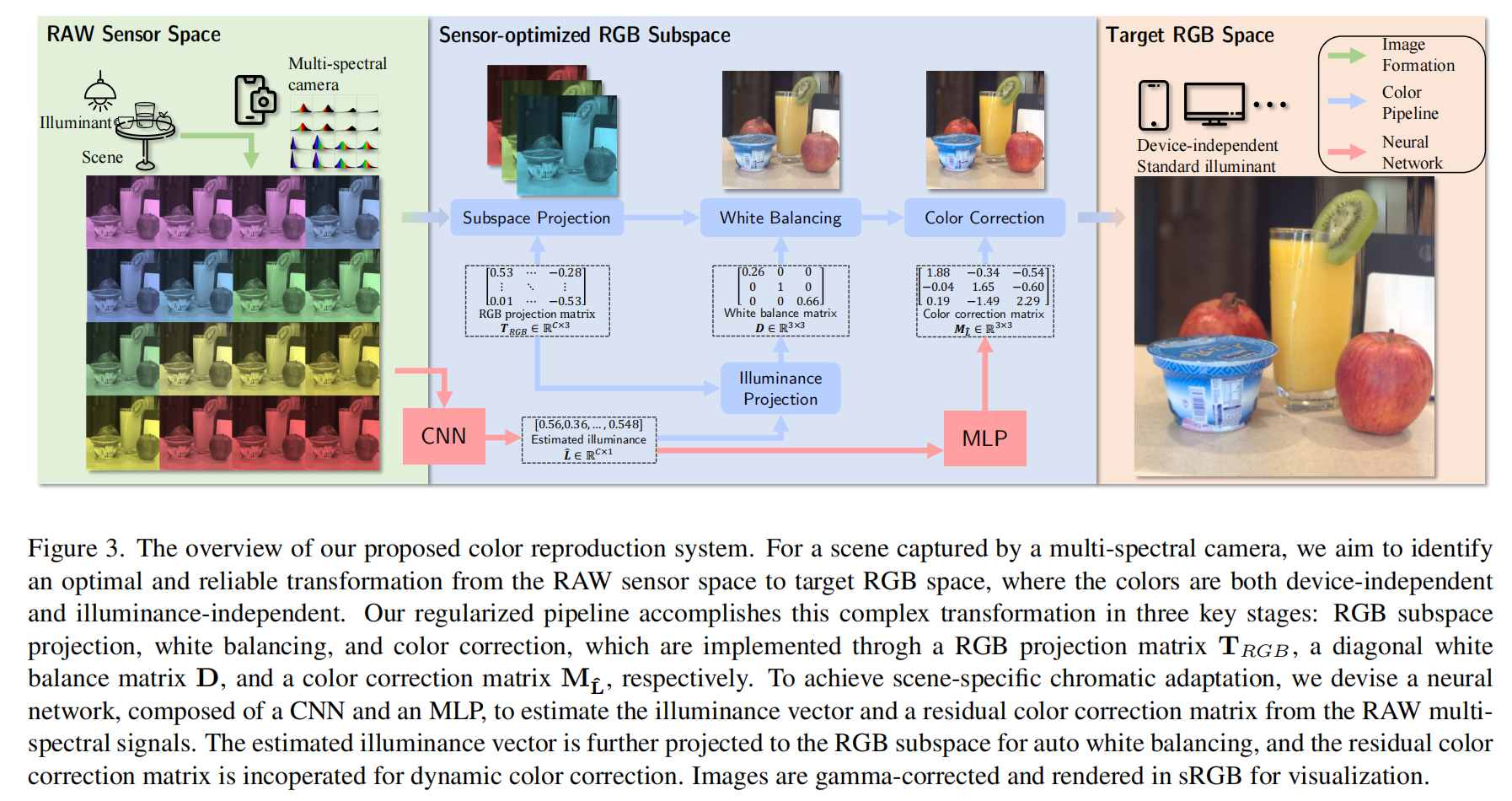
- 图 3 本文提出的色彩还原系统总览如下:对于多光谱相机拍摄的场景,我们旨在构建从原始传感器空间到目标 RGB 空间的最优且可靠转换方法,确保转换后的色彩既具备设备无关性,也具备光照无关性。我们的正则化流程通过三个关键阶段完成这一复杂转换,分别是 RGB 子空间投影、白平衡调整与色彩校正。这三个阶段分别通过 RGB 投影矩阵 TRGB\boldsymbol{T}{\text{RGB}}TRGB、对角白平衡矩阵 D\boldsymbol{D}D 和色彩校正矩阵 ML^\boldsymbol{M}{\hat{L}}ML^ 实现。为实现场景特异性色适应,我们设计了一个由卷积神经网络(CNN)和多层感知器(MLP)组成的神经网络,用于从原始多光谱信号中估计光照向量与残差色彩校正矩阵。估计得到的光照向量会进一步投影到 RGB 子空间以实现自动白平衡,残差色彩校正矩阵则会用于动态色彩校正。所有图像均经过伽马校正,并以 sRGB 格式渲染以用于可视化呈现。
与标准 RGB 色彩流程不同,多光谱图像(MSI)的引入给系统设计带来了一个根本性挑战:我们无法在多通道空间中定义 "白色"。"白色"(R=G=B)及各类色彩仅在三通道空间(通常为 CIE XYZ 空间)中具有实际意义。为解决这一问题并实现稳健的色彩再现,我们为多光谱相机设计了一套经过精心正则化的色彩流程。如图 3 所示,该色彩流程通过三个关键阶段完成复杂的变换 T\boldsymbol{T}T:RGB 子空间投影、白平衡调整与色彩校正。首先,我们利用子空间投影矩阵 TRGB∈RC×3\boldsymbol{T}{\text{RGB}} \in \mathbb{R}^{C \times 3}TRGB∈RC×3,将多光谱原始响应 IMSI\boldsymbol{I}{\text{MSI}}IMSI 投影到三通道 RGB 空间。我们假设该 RGB 子空间满足冯・克里兹(von Kries)假说。由此,我们基于从估计场景光照向量L^∈RC×1\hat{\boldsymbol{L}} \in \mathbb{R}^{C \times 1}L^∈RC×1中获取的白平衡系数W∈R3×1\boldsymbol{W} \in \mathbb{R}^{3 \times 1}W∈R3×1,推导得到一个用于白平衡调整的对角矩阵D∈R3×3\boldsymbol{D} \in \mathbb{R}^{3 \times 3}D∈R3×3。最后,我们通过应用色彩校正矩阵ML^\boldsymbol{M}_{\hat{L}}ML^,将经过白平衡调整的图像进一步转换到目标 RGB 空间。综上,我们的色彩流程可表述为:
IRGB=IMSI⋅TRGB⋅D⋅ML^D=diag(W)W=L^⋅TRGB(4) \boldsymbol{I}{\text{RGB}} = \boldsymbol{I}{\text{MSI}} \cdot \boldsymbol{T}{\text{RGB}} \cdot \boldsymbol{D} \cdot \boldsymbol{M}{\hat{L}} \\ \boldsymbol{D} = \text{diag}(\boldsymbol{W})\\ \boldsymbol{W} = \hat{\boldsymbol{L}} \cdot \boldsymbol{T}_{\text{RGB}} \tag{4} IRGB=IMSI⋅TRGB⋅D⋅ML^D=diag(W)W=L^⋅TRGB(4)
其中,diag(⋅)\text{diag}(\cdot)diag(⋅) 表示由一个 n×1n \times 1n×1 维向量生成 n×nn \times nn×n 维对角矩阵的运算。
通过该色彩流程,我们遵循分而治之(divide-and-conquer)范式的核心思想,对变换矩阵 T\boldsymbol{T}T 的构成进行正则化处理。RGB 子空间投影矩阵TRGB\boldsymbol{T}_{\text{RGB}}TRGB的主要目标,是确定一个适宜的 RGB 子空间以辅助实现计算色彩恒常性,而非匹配人眼的色彩感知特性。需注意,该投影过程应与场景无关(scene-agnostic),即它仅捕捉传感器自身的特性,而非针对特定场景设计。因此,我们从变换矩阵 T\boldsymbol{T}T 中分离出光照向量 L\boldsymbol{L}L。该向量被视为场景特异性变量(scene-specific variable),并在后续色彩恒常性变换的确定中发挥关键作用。最后,我们通过引入两个组件对完整的 3×3 色彩校正操作进行拆分:一个是由白平衡系数 W\boldsymbol{W}W 推导得到的对角矩阵 D\boldsymbol{D}D,另一个是经过正则化处理(每行元素之和为 1)的色彩校正矩阵 M\boldsymbol{M}M。前者用于校正无彩色(achromatic colors),后者则通过处理剩余的有彩色(chromatic colors),对校正过程起到补充作用。
Spectral Prior-guided Optimization
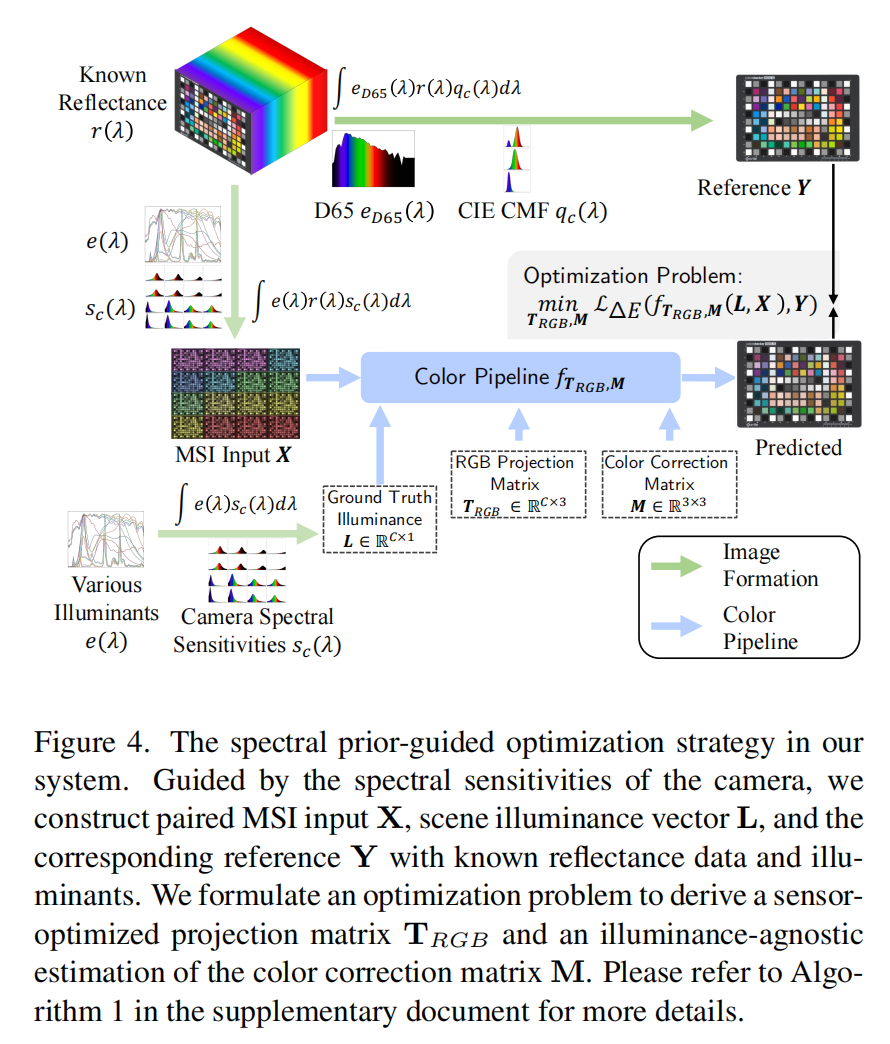
- 图 4 我们系统中的光谱先验引导优化策略如下:在相机光谱灵敏度的引导下,我们利用已知的反射率数据和光源,构建多光谱输入X\boldsymbol{X}X、场景光照向量L\boldsymbol{L}L及对应参考值Y\boldsymbol{Y}Y的配对数据。我们通过构建优化问题,求解得到传感器优化的投影矩阵TRGB\boldsymbol{T}_{\text{RGB}}TRGB以及与光照无关的色彩校正矩阵M\boldsymbol{M}M估计值。
基于上述色彩流程的公式推导,我们提出一种光谱先验引导的优化策略,用于确定适用于计算色彩恒常性的 RGB 子空间。如图 4 所示,该优化策略旨在求解子空间投影矩阵TRGB\boldsymbol{T}_{\text{RGB}}TRGB,以及与光照无关的色彩校正矩阵M\boldsymbol{M}M估计值。为实现稳健估计,我们从各类已知反射率数据库 R\mathcal{R}R 和已知光源 E\mathcal{E}E中,构建多光谱输入与参考 RGB 的配对数据。
Xi=∫λei(λ)ri(λ)sc(λ)dλYi=∫λeD65(λ)ri(λ)qc(λ)dλ(5)\boldsymbol{X}i = \int{\lambda} e_i(\lambda) r_i(\lambda) s_c(\lambda) d\lambda \quad \boldsymbol{Y}i = \int{\lambda} e_{\text{D65}}(\lambda) r_i(\lambda) q_c(\lambda) d\lambda \tag{5} Xi=∫λei(λ)ri(λ)sc(λ)dλYi=∫λeD65(λ)ri(λ)qc(λ)dλ(5)
其中 ri∈Rr_i \in \mathcal{R}ri∈R,ei∈Ee_i \in \mathcal{E}ei∈E,i=1,2,3,...,Ni = 1, 2, 3, ..., Ni=1,2,3,...,N。
其中,eD65(λ)e_{\text{D65}}(\lambda)eD65(λ) 表示标准照明体 D65 的光谱功率分布(SPD),scs_csc 为多光谱相机的光谱灵敏度,qcq_cqc 是 CIE 1931 色匹配函数(CMF);rir_iri 从反射率数据库 R\mathcal{R}R 中随机采样得到,eie_iei 从光源集合 E\mathcal{E}E 中随机采样得到,NNN 为数据对的总数。此外,对应的真实光照向量可通过 Li=∫λei(λ)sc(λ)dλL_i = \int_{\lambda} e_i(\lambda) s_c(\lambda) d\lambdaLi=∫λei(λ)sc(λ)dλ 计算得出。在此,我们将式(4)中定义的色彩流程记为 fTRGB,Mf_{\boldsymbol{T}_{\text{RGB}}, \boldsymbol{M}}fTRGB,M。那么,光谱先验引导的优化问题可表述为:
minTRGB,M1N∑i=1NLΔE(fTRGB,M(Xi,Li),Yi)(6) \min_{\boldsymbol{T}{\text{RGB}}, \boldsymbol{M}} \frac{1}{N} \sum{i=1}^{N} L_{\Delta E}\left(f_{\boldsymbol{T}_{\text{RGB}}, \boldsymbol{M}}(\boldsymbol{X}_i, L_i), \boldsymbol{Y}_i\right) \tag{6} TRGB,MminN1i=1∑NLΔE(fTRGB,M(Xi,Li),Yi)(6)
其中,LΔEL_{\Delta E}LΔE 是用于衡量色差值的距离函数,我们采用了公认的 dE2000 色差公式 [51]。通过这一优化过程,我们得到最优的 TRGB\boldsymbol{T}_{\text{RGB}}TRGB 以及与光照无关的 M\boldsymbol{M}M 估计值,从而确定适用于色彩恒常性的 RGB 子空间。正如后文图 6 所示,相较于标准 RGB 流程中常用的 CIE XYZ 空间选择,我们通过这种端到端(end-to-end)优化过程,进一步确定了一个更优的、针对传感器优化的子空间。
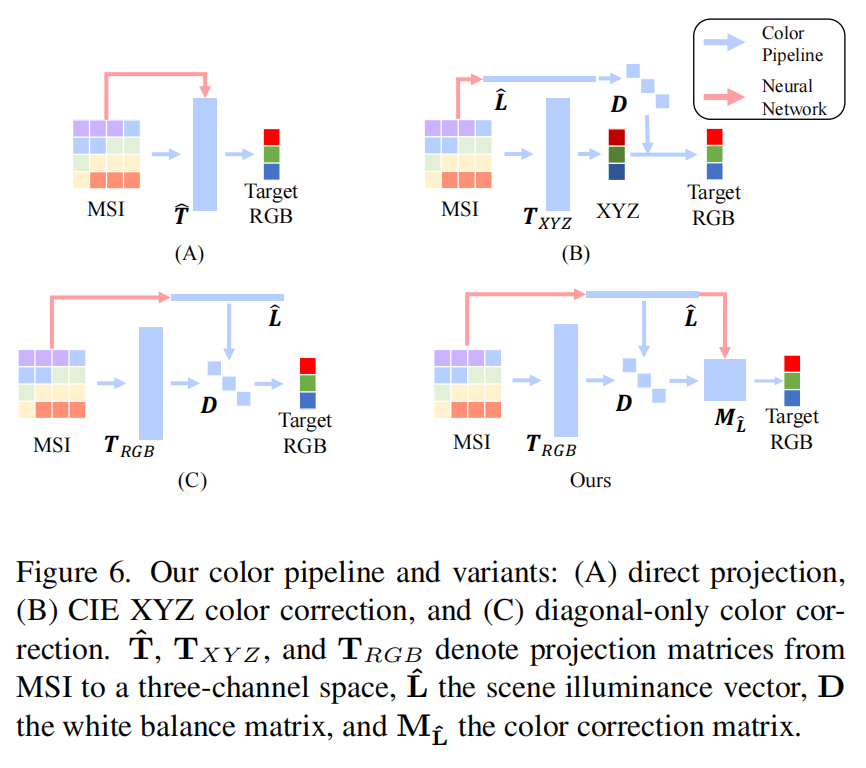
- 图 6 我们的色彩流程及其变体包括三类:(A)直接投影、(B)CIE XYZ 色彩校正、(C)仅对角色彩校正。其中,T^\hat{\boldsymbol{T}}T^、TXYZ\boldsymbol{T}{\text{XYZ}}TXYZ、TRGB\boldsymbol{T}{\text{RGB}}TRGB 均表示从多光谱图像(MSI)到三通道空间的投影矩阵;L^\hat{\boldsymbol{L}}L^ 为场景光照向量;D\boldsymbol{D}D 为白平衡矩阵;ML^\boldsymbol{M}_{\hat{L}}ML^ 为色彩校正矩阵。
Learning-based Chromatic Adaptation
在利用TRGB\boldsymbol{T}{\text{RGB}}TRGB确定了适用于计算色彩恒常性的传感器优化 RGB 子空间后,我们接下来引入一种基于学习的 chromatic adaptation 神经网络,用于将该子空间中的 RGB 色彩校正至目标 RGB 空间。如图 3 所示,该 chromatic adaptation 神经网络包含两个主要组件:卷积神经网络(CNN)和多层感知机(MLP)网络。我们从多光谱图像IMSI\boldsymbol{I}{\text{MSI}}IMSI中估计场景光照向量L^\hat{\boldsymbol{L}}L^,并根据估计的L^\hat{\boldsymbol{L}}L^预测色彩校正矩阵M\boldsymbol{M}M的光照自适应残差。为实现白平衡,我们利用TRGB\boldsymbol{T}{\text{RGB}}TRGB将估计的光照向量L^\hat{\boldsymbol{L}}L^投影到 RGB 子空间,得到白平衡系数W\boldsymbol{W}W。这些系数用于构建对角矩阵D\boldsymbol{D}D,以实现自动白平衡。随后,将预测的色彩校正矩阵光照自适应残差与光照无关估计值相结合,得到用于动态色彩校正的最终色彩校正矩阵ML^\boldsymbol{M}{\hat{L}}ML^。对于 CNN,我们选择 YOLOv4 [11] 中的 CSPDNet 架构,因其结构简洁;当然,更先进的架构也同样适用。
色适应网络的训练包含两个损失函数:用于光照估计的角度误差(AE)和用于光照自适应色彩校正矩阵的均方根误差(RMSE)。估计光照向量L^\hat{\boldsymbol{L}}L^与真实光照向量L\boldsymbol{L}L之间的角度误差(AE)定义为:
LAE(L^,L)=cos−1 (L^TL∥L^∥∥L∥)(7) \mathcal{L}_{\text{AE}}(\hat{\boldsymbol{L}}, \boldsymbol{L}) = \cos^{-1}\!\left( \frac{\hat{\boldsymbol{L}}^T \boldsymbol{L}}{\|\hat{\boldsymbol{L}}\| \|\boldsymbol{L}\|} \right) \tag{7} LAE(L^,L)=cos−1(∥L^∥∥L∥L^TL)(7)
对于每个光源,我们通过固定式(6)中的 TRGB\boldsymbol{T}{\text{RGB}}TRGB 来优化对应的色彩校正矩阵 MGT\boldsymbol{M}{\text{GT}}MGT。因此,动态色彩校正的损失函数可表述为:
LRMSE(ML^,ML)=∥ML^−ML∥(8) \mathcal{L}{\text{RMSE}}(\boldsymbol{M}{\hat{L}}, \boldsymbol{M}L) = \sqrt{\|\boldsymbol{M}{\hat{L}} - \boldsymbol{M}_L\|} \tag{8} LRMSE(ML^,ML)=∥ML^−ML∥ (8)
为便于色适应网络的训练,我们提出了一种数据增强策略:利用一个 "颜色 - 反射率检索字典",从易于获取的 sRGB 图像中生成高光谱反射率数据,进而用于合成丰富的多光谱输入与对应标准 RGB 表示的训练对。如图 5 所示,我们构建该颜色 - 反射率字典的方式为:将单像素反射率数据投影至 sRGB 色域,并对映射到相同 RGB 值的反射率样本取平均值。

- 图 5 多光谱数据增强策略如下:上方:我们通过将反射率数据投影至 sRGB 色域,构建 sRGB 值与对应高光谱反射率之间的映射字典。下方:我们对一系列高质量 sRGB 图像进行查询,以获取全面的高光谱反射率数据集。借助该数据集,我们通过图像形成模型合成多光谱输入(MSI)和参考图像。
我们通过在高质量公开 sRGB 数据集(如 DIV2K [3]、MultiIllum [55] 等)中逐像素检索该字典,构建了一个大规模合成多光谱反射率数据集。利用这个合成反射率数据集,我们可以通过与式(5)类似的图像形成过程,合成多光谱图像 IMSI\boldsymbol{I}{\text{MSI}}IMSI、光照向量 L\boldsymbol{L}L 和参考 RGB 图像 IRGB\boldsymbol{I}{\text{RGB}}IRGB 的训练对。在此,我们做出一个重要假设:这些 sRGB 图像在参考照明体 D65 下已达到良好的白平衡状态。借助这些合成训练对,我们对色适应网络进行预训练,以提升其稳健性和泛化能力。随后,我们使用真实反射率数据集对网络进行微调,进一步提高其在真实场景中的性能。