🌟 题目描述
给定一个链表的头节点 head,返回链表开始入环的第一个节点。如果链表无环,则返回 null。
💡 注意:不允许修改链表结构。
示例 1:
makefile
输入: head = [3,2,0,-4], pos = 1
输出: 返回索引为 1 的节点(值为 2)
解释: 链表有一个环,尾部连接到第二个节点。示例 2:
ini
输入: head = [1,2], pos = 0
输出: 返回索引为 0 的节点(值为 1)示例 3:
ini
输入: head = [1], pos = -1
输出: null🔍 问题分析
这是一道经典的 环检测 + 环入口定位 问题。关键点:
- 如何判断链表是否有环?
- 如果有环,如何找到环的起始节点?
直接遍历会陷入死循环,所以需要更聪明的方法------快慢指针(Floyd 循环查找算法) 。
💡 核心思路:Floyd 判圈算法
✅ 第一步:用快慢指针判断是否存在环
slow指针每次走一步;fast指针每次走两步;- 若存在环,两者一定会相遇(因为快指针会追上慢指针);
- 若无环,
fast会先到达null。
✅ 第二步:找到环的入口节点
当快慢指针相遇后,从头节点和相遇点同时出发,每次走一步,再次相遇的点就是环的入口。
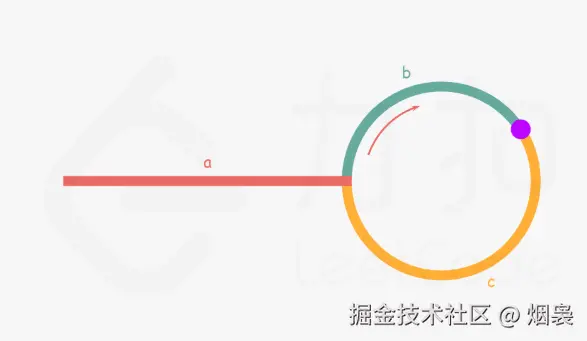
🧠 数学证明简述:
设:
- 链表头部到环入口距离为
a- 环的长度为
b- 相遇点距离入口为
c则:
- 慢指针走了:
a + c- 快指针走了:
a + c + k*b(k 是整数)- 因为快指针速度是慢指针的 2 倍:
2(a + c) = a + c + k*b- 推出:
a = k*b - c- 即:从头节点走
a步,和从相遇点走a步,会在入口处相遇!
✅ JavaScript 实现(完整代码)
ini
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val === undefined ? 0 : val)
* this.next = (next === undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
var detectCycle = function(head) {
let slow = head;
let fast = head;
// 第一步:快慢指针找相遇点
while (fast && fast.next) {
slow = slow.next;
fast = fast.next.next;
if (slow === fast) {
// 找到环,进入第二步:找入口
let x1 = head; // 从头开始
let x2 = fast; // 从相遇点开始
while (x1 !== x2) {
x1 = x1.next;
x2 = x2.next;
}
return x1; // 相遇点即为环的入口
}
}
// 无环,返回 null
return null;
};🧠 图解演示(以 [3→2→0→-4→2] 为例)
yaml
链表:3 → 2 → 0 → -4 → ↲ 2(环)
↑ ↑
| |
-----------------
1. 快慢指针移动:
slow: 3 → 2 → 0 → -4 → 2
fast: 3 → 0 → 2 → -4 → 2 → 0 → 2 → ...
2. 在节点 2 相遇(快慢指针相等)
3. 重置 x1 = head(3), x2 = 相遇点(2)
x1: 3 → 2
x2: 2 → 0 → -4 → 2 → ...
在节点 2 再次相遇 → 返回该节点📊 复杂度分析
| 项目 | 复杂度 |
|---|---|
| 时间复杂度 | O(n) ------ 最多遍历两次链表 |
| 空间复杂度 | O(1) ------ 只使用常数额外空间 |
✅ 优势:无需哈希表,不修改链表,适用于大链表场景。
🛠️ 面试常见问题
❓ "为什么相遇后,从头和相遇点同时走能相遇于入口?"
回答:这是由数学关系
a = k*b - c决定的,两个指针走的路径总长相同,最终会在入口处相遇。
❓ "能否用哈希表解决?"
可以,但空间复杂度为 O(n),而快慢指针法是 O(1),更优。
❓ "如果链表很长,快指针会不会越界?"
不会,因为
while(fast && fast.next)已经做了安全判断。
✅ 总结
其实这题就先设置两个指针慢的一步一步走而快的则两步两步走如果存在环则必定相遇,如果相遇就可以通过这幅图推出a=c+(n−1)(b+c)那就差不多能写出来了