此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下:
- 原课程视频链接:[双语字幕]吴恩达深度学习deeplearning.ai
- github课程资料,含课件与笔记:吴恩达深度学习教学资料
- 课程配套练习(中英)与答案:吴恩达深度学习课后习题与答案
本周为第二课的第二周内容,和题目一样,本周的重点是优化算法,即如何更好,更高效地更新参数帮助拟合的算法,还是离不开那句话:优化的本质是数学 。
因此,在理解上,本周的难道要相对较高一些,公式的出现也会更加频繁。
当然,我仍会补充一些更基础的内容来让理解的过程更丝滑一些。
本篇的内容关于Mini-batch 梯度下降,是对之前梯度下降的补充和完善。
1. Mini-batch 梯度下降法
其实我们早就在使用这个方法了,现在来系统的阐述一下。
如果你有些遗忘了梯度下降法本身的概念,可以回看之前的笔记:梯度下降法
而发展出的随机梯度,Mini-batch 梯度,batch 梯度只是一次迭代中使用样本数量的不同。
1.1 随机梯度下降法
实际上,在第一周学习向量化之前,我们理解的梯度下降法就是随机梯度下降法(Stochastic Gradient Descent,SGD)。
具体展开概念:
随机梯度下降法是一种优化算法,常用于训练机器学习模型,尤其是在深度学习中。随机梯度下降法 在每次更新时只使用一个样本 来计算梯度并进行参数更新,而与之相对的批量梯度下降法,就是使用全部样本计算梯度并更新。
也就是说,在一次训练中,我们有多少个样本,就会进行多少次参数更新。
现在展开几个小问题。
(1)使用随机梯度下降和是否向量化的关系?
之前在向量化部分我们提到,使用向量化是为了在代码中避免显示的for循环,以并行提高效率。
通过向量化,我们可以并行地进行多个样本的训练,用多个样本的损失更新参数。
那现在使用随机梯度下降,我们一次迭代只用一个样本,那是不是就代表我们要使用非向量化的输入?
先说结论:随机梯度下降 ≠ 非向量化 ,因为 "是否向量化" 和 "是否使用随机梯度" 是两个不同维度的问题:
- 向量化 → 指的是代码实现方式(是否用for循环逐样本计算)。
- SGD / Mini-batch / Batch GD → 指的是算法在每次更新参数时使用多少样本。
也就是说:
我们完全可以向量化地实现SGD,即一次用一个样本,但仍然用矩阵操作计算,二者可以并存。
举个例子:
就像做饭时,"你一次炒几份菜"与"你用不用电磁炉这种高效设备"是两件不同的事情 。
是否向量化,就像是你用不用电磁炉、用不用多头灶台,它决定的是你做菜的效率,是工具层面的提升。
而随机梯度下降、Batch 或 Mini-batch 则是你每次炒几人份:一次炒一份、一次炒十份、还是一次炒满整锅,这是做饭方式的选择。
你完全可以同时做到"使用电磁炉(向量化)"并且"每次只炒一份(SGD)"。两者互不矛盾,只是一个管"快不快",一个管"每次做多少"。
这就是二者的区别。

(2)随机梯度下降的优劣?
先总地看一下这个算法的优劣:
| SGD 的特点 | 它带来的优点 | 它造成的缺点 |
|---|---|---|
| 每次只使用 1 个样本更新(高频、小步、噪声大) | 更新非常频繁,模型能更快开始学习;带噪声的更新更容易跳出局部最优 | 噪声过大导致收敛不稳定;损失曲线抖动明显;学习率一旦偏大容易发散 |
| 每次计算量小(占用内存少) | 不需要大显存,小设备也能训练;适合超大规模数据 | 单次处理数据量太小,无法用好 GPU 的并行能力,整体训练速度反而偏慢 |
| 更新方向依赖单一样本(信息量少) | 每次更新成本低,可以快速迭代 | 单一样本可能不能代表整体趋势,更新方向偏差大,需要更多 epoch 才能收敛 |
| 对于其中第一点可能不太清晰,我们来详细解释一下。 |
(3)SGD的收敛不稳定现象
我们刚刚提到,"每次只使用一个样本更新"会带来一个核心影响:更新方向带有更多的噪声 。
为了更好的理解这点,我们依旧把最小化损失类比成从山谷下山。
如果我们使用批量梯度下降(Batch GD),每次更新方向是所有样本平均后的梯度,因此方向非常稳定,像是沿着山谷中心线稳稳地往下走。
但 SGD 不同。因为它每次只使用一个样本,如果这个样本是个"好样本",那更新后损失就向谷底走一步,如果下一个样本是噪声样本,更新后损失甚至可能回反着走回去。这样每次更新对单一样本的依赖就会带来损失的"振荡",导致收敛不稳定,就像一个不准的导航,让你绕着弯下山。

1.2 Mini-batch 梯度下降法
Mini-batch 梯度下降法 是介于Batch GD 和SGD 之间的一种折中方案。它每次更新使用一个小批量样本,而不是全部样本或单个样本。
举个实例,假设我们有 1000 个样本,设置 mini-batch 大小为 10,那么每次迭代我们会随机选 10 个样本计算平均梯度,并更新参数,这样下来,一个 epoch 需要进行 (1000 / 10 = 100) 次参数更新。
(1)Mini-batch 的优缺点
| Mini-batch 特点 | 它带来的优点 | 它造成的缺点 |
|---|---|---|
| 每次使用部分样本更新 | 更新方向比 SGD 稳定,损失曲线波动小,收敛更可靠 | 每次更新仍存在一定噪声,收敛路径不是完全平滑 |
| 计算量适中,可利用并行 | 可以充分利用 GPU 并行能力,训练速度快 | mini-batch 太小会像 SGD 一样噪声大,太大又趋向 Batch GD,灵活性降低 |
| 在噪声和稳定性之间折中 | 既有一定跳出局部最优的能力,又不会像 SGD 那样过于颠簸 | 超参数(batch size)需要调节,不同任务最优值不同 |
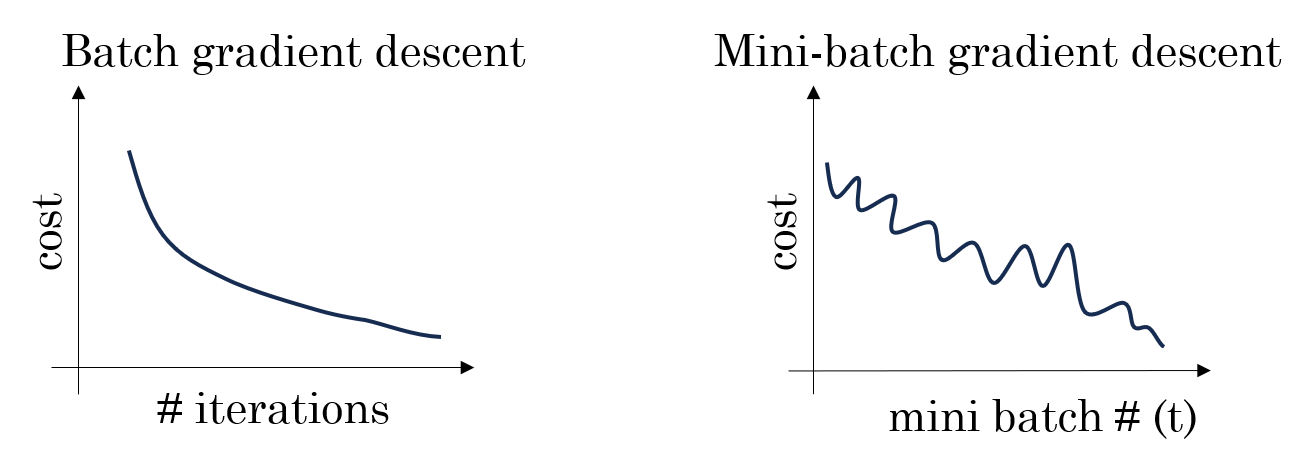
(2)Mini-batch 的收敛表现
在"下山"比喻下,Mini-batch 就像是手里拿着局部准确的地图:
- 噪声被部分平滑:每次看几个人的样本,方向不会因为单一样本异常而大幅偏离。
- 路径仍有微小抖动:相比 Batch GD,仍然可以"微调"路线,更灵活地适应复杂地形。
- 训练效率较高 :每次更新占用内存适中,可以充分利用 GPU 并行,整体训练时间比 SGD 更短。
总的来说,Mini-batch 在性能和成本上的平衡让其成为了我们的最佳选择。
但Mini-batch也带来一个新的超参数:批次大小(Batch size)。
(3)Batch size 的选择
Mini-batch 的核心超参数是 batch size,一般来说:
- 小 batch(如 1~32) → 噪声大,收敛不稳定,但可能帮助跳出局部最优
- 中 batch(如 64~256) → 收敛稳定,训练速度较快,适合大部分任务
- 大 batch (如 1024 以上) → 接近 Batch GD,收敛平稳,但对 GPU 显存要求高
因此,我们通常的选择是这样的: - 小数据集 → 可用大 batch,保证稳定收敛
- 大数据集 → 使用中等 batch,兼顾效率与稳定性
- 尽量避免过小或过大的批次大小。