写在前面:

牛客每日一题持续更新中!
今天给亦菲和彦祖们带来的是【模板】二维前缀和
是一个模版题 题目如下:
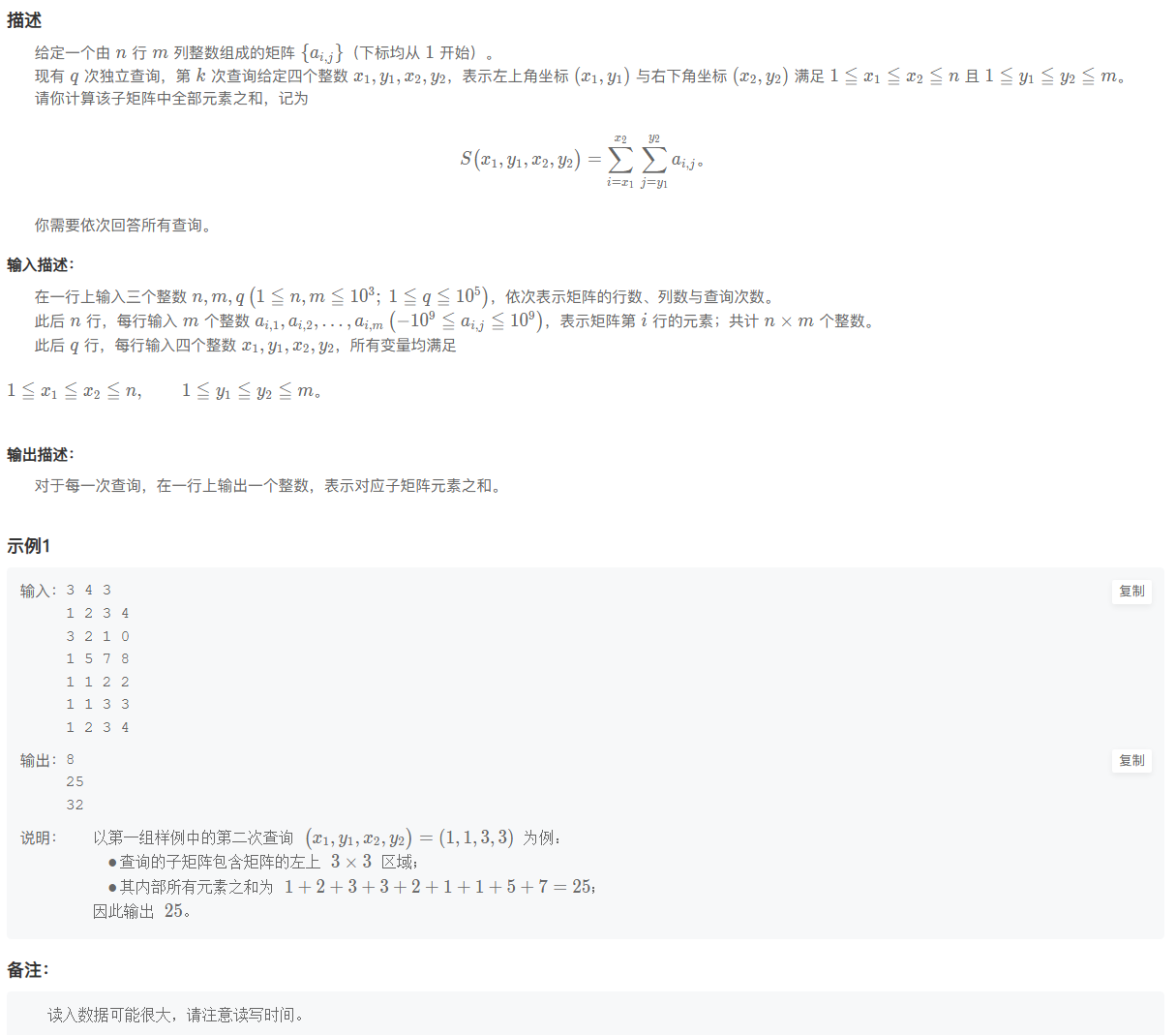
题意整理。
- 给定一个n行m列的矩阵。
- 有q次查询,每次查询给定子矩阵的左上角坐标和右下角坐标,输出子矩阵中所有元素的累加和。
1.解题思路
- 我们可以开个二维数组 a[i][j] 表示前i行且列数<=j 的所有元素之和,如果i=3,j=4那么就是下图所有元素之和,然后对矩阵进行预处理,得到对应的前缀和矩阵。
- 利用前缀和矩阵相应区域的加减运算,即可得到对应子矩阵中所有元素的累加和。
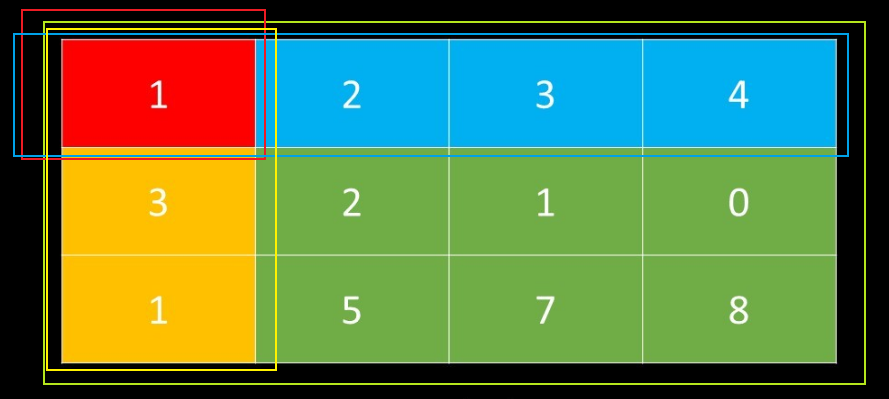
- 假如我们要求如图中绿色区域的矩阵元素和,
- 我们可以用图中绿色框框内的元素和 - 蓝色框框内的元素之和 - 黄色框框内的元素之和 + 红色框框之和(因为红色框框内元素和被减了两次 所以需要加一次)
2.代码实现:
C/C++版本:
cpp
#include<bits/stdc++.h> // 包含所有标准库头文件
using namespace std;
long long a[1010][1010]; // 定义二维数组,同时作为原始矩阵和前缀和矩阵
int main(){
int n, m, q;
cin >> n >> m >> q; // 输入矩阵行数n,列数m,查询次数q
int i, j;
// 第一步:按行计算列方向的前缀和
for(i = 1; i <= n; i++){
for(j = 1; j <= m; j++){
cin >> a[i][j]; // 输入矩阵元素
// 计算列前缀和:a[i][j] = 原矩阵值 + 上方元素的前缀和
// 此时a[i][j]表示从(1,1)到(i,j)的矩形中,第j列从第1行到第i行的和
a[i][j] += a[i-1][j];
}
}
// 第二步:按列计算行方向的前缀和,完成二维前缀和的构建
for(j = 1; j <= m; j++){
for(i = 1; i <= n; i++){
// 计算二维前缀和:a[i][j] = 当前列前缀和 + 左侧列的前缀和
// 此时a[i][j]表示从(1,1)到(i,j)的整个矩形的元素和
a[i][j] += a[i][j-1];
}
}
// 处理每个查询
while(q--){
int x_1, y_1, x_2, y_2;
cin >> x_1 >> y_1 >> x_2 >> y_2; // 输入查询的矩形区域
// 计算子矩阵和:利用二维前缀和的性质
// 总和 = 大矩形 - 左边矩形 - 上边矩形 + 左上角矩形(因为被减了两次)
cout << a[x_2][y_2] - a[x_1-1][y_2] - a[x_2][y_1-1] + a[x_1-1][y_1-1] << endl;
}
return 0;
}Python版本:
python
import sys
def main():
data = sys.stdin.read().split()
it = iter(data)
# 读取n, m, q
n = int(next(it)); m = int(next(it)); q = int(next(it))
# 创建二维数组,多开一圈用于处理边界情况
# 使用0-indexed,但保留第0行和第0列为0
a = [[0] * (m + 1) for _ in range(n + 1)]
# 第一步:按行计算列方向的前缀和
for i in range(1, n + 1):
for j in range(1, m + 1):
val = int(next(it))
# a[i][j] = 原矩阵值 + 上方元素的前缀和
a[i][j] = val + a[i-1][j]
# 第二步:按列计算行方向的前缀和,完成二维前缀和
for j in range(1, m + 1):
for i in range(1, n + 1):
# a[i][j] = 当前列前缀和 + 左侧列的前缀和
a[i][j] += a[i][j-1]
# 处理每个查询
results = []
for _ in range(q):
x1 = int(next(it)); y1 = int(next(it))
x2 = int(next(it)); y2 = int(next(it))
# 计算子矩阵和:大矩形 - 左边 - 上边 + 左上角
total = (a[x2][y2] - a[x1-1][y2] -
a[x2][y1-1] + a[x1-1][y1-1])
results.append(str(total))
# 输出所有结果
print("\n".join(results))
if __name__ == "__main__":
main()Java版本:
java
import java.util.*;
import java.io.*;
public class Main {
public static void main(String[] args) {
FastReader sc = new FastReader();
int n = sc.nextInt(); // 行数
int m = sc.nextInt(); // 列数
int q = sc.nextInt(); // 查询次数
// 创建二维数组,多开一圈用于处理边界情况
long[][] a = new long[n + 1][m + 1];
// 第一步:按行计算列方向的前缀和
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
long val = sc.nextLong();
// a[i][j] = 原矩阵值 + 上方元素的前缀和
a[i][j] = val + a[i - 1][j];
}
}
// 第二步:按列计算行方向的前缀和,完成二维前缀和
for (int j = 1; j <= m; j++) {
for (int i = 1; i <= n; i++) {
// a[i][j] = 当前列前缀和 + 左侧列的前缀和
a[i][j] += a[i][j - 1];
}
}
// 处理每个查询
StringBuilder sb = new StringBuilder();
for (int i = 0; i < q; i++) {
int x1 = sc.nextInt();
int y1 = sc.nextInt();
int x2 = sc.nextInt();
int y2 = sc.nextInt();
// 计算子矩阵和:大矩形 - 左边 - 上边 + 左上角
long result = a[x2][y2] - a[x1 - 1][y2]
- a[x2][y1 - 1] + a[x1 - 1][y1 - 1];
sb.append(result).append("\n");
}
System.out.print(sb.toString());
}
// 快速输入类,提高Java输入效率
static class FastReader {
BufferedReader br;
StringTokenizer st;
public FastReader() {
br = new BufferedReader(new InputStreamReader(System.in));
}
String next() {
while (st == null || !st.hasMoreElements()) {
try {
st = new StringTokenizer(br.readLine());
} catch (IOException e) {
e.printStackTrace();
}
}
return st.nextToken();
}
int nextInt() {
return Integer.parseInt(next());
}
long nextLong() {
return Long.parseLong(next());
}
}
}3.复杂度分析
- 时间复杂度:需要遍历数组中所有元素构建前缀和数组,预处理的时间复杂度为O(n∗m)O(n∗m),每次查询只需进行一次运算,所以查询的时间复杂度为O(1)O(1)。
- 空间复杂度:需要额外长度为(n+1)∗(m+1)(n+1)∗(m+1)的前缀和矩阵,所以空间复杂度为O(n∗m)O(n∗m)。
好了,各位码友,代码已经调试通过,文章也已commit,就等各位的push了。点赞不要 //TODO,关注务必 star!
写在后面:
