脉冲在克尔效应下的频谱展宽仿真：原理与 MATLAB 实现

一、背景：脉冲频谱展宽的物理机制

当强激光脉冲在具有克尔效应的介质中传播时，自相位调制（SPM） 会导致脉冲的频谱展宽。其核心原理是：

脉冲的光强随时间变化（中心强、边缘弱）
克尔效应使折射率随光强变化（\(n = n_0 + n_2 I(t)\)）
不同时刻的相位变化不同（\(\Delta\phi(t) \propto I(t)\)），形成频率调制（啁啾）
相位随时间的变化（\(\frac{d\phi}{dt}\)）直接导致频谱展宽

这种效应在超短脉冲激光技术、光通信中具有重要应用，是实现超连续谱光源的核心机制之一。

二、仿真思路

脉冲模型：采用高斯脉冲，时间分布为 \(A(t) = \exp(-\frac{t^2}{2T_0^2})\)，光强 \(I(t) \propto |A(t)|^2\)
SPM 相位计算：非线性相位 \(\phi_{\text{SPM}}(t) = \frac{2\pi n_2 L}{\lambda} I(t)\)，其中 L 为传播距离
频谱计算：通过傅里叶变换将时域脉冲转换到频域，观察频谱展宽
参数对比：改变脉冲功率或传播距离，分析频谱展宽的变化规律

三、完整 MATLAB 代码实现

Matlab 复制代码

% 脉冲在克尔效应下的频谱展宽仿真
% 功能：模拟高斯脉冲通过非线性介质时的自相位调制(SPM)及频谱展宽现象
clear; clc; close all;

%% 1. 参数设置
% 物理参数
lambda = 1550e-9;          % 波长(1550nm，通信常用)
n0 = 1.45;                 % 线性折射率
n2 = 2.6e-20;              % 克尔系数(m²/W)
L = 100;                   % 传播距离(m)
T0 = 10e-12;               % 脉冲宽度(10ps，半高全宽约23.5ps)
P0_list = [5, 20, 50];     % 不同峰值功率(W)，用于对比展宽效果

% 时间网格设置
t_max = 50e-12;            % 时间范围(-50ps ~ 50ps)
Nt = 2048;                 % 时间采样点数(确保傅里叶变换精度)
t = linspace(-t_max, t_max, Nt);  % 时间向量

%% 2. 脉冲与频谱计算
% 预分配存储变量
A_all = cell(length(P0_list), 1);    % 时域脉冲
phi_spm_all = cell(length(P0_list), 1);  % SPM相位
spec_all = cell(length(P0_list), 1);   % 频谱

for p = 1:length(P0_list)
    P0 = P0_list(p);  % 当前峰值功率
    
    % 1. 计算时域高斯脉冲
    % 振幅：A(t) = sqrt(P0) * exp(-t²/(2T0²))
    A = sqrt(P0) * exp(-t.^2 / (2 * T0^2));
    A_all{p} = A;
    
    % 2. 计算自相位调制(SPM)引起的相位变化
    I = abs(A).^2;  % 光强(I ∝ |A|²)
    delta_n = n2 * I;  % 非线性折射率变化
    phi_spm = (2 * pi * delta_n * L) / lambda;  % SPM相位
    phi_spm_all{p} = phi_spm;
    
    % 3. 计算脉冲频谱(含SPM效应)
    % 带相位的脉冲：A(t) * exp(i*phi_spm)
    A_spm = A .* exp(1i * phi_spm);
    % 傅里叶变换到频域(加窗函数减少频谱泄漏)
    spec = fftshift(fft(A_spm .* hanning(Nt)));
    spec = abs(spec).^2;  % 频谱强度
    spec_all{p} = spec;
end

%% 3. 频率轴计算(用于频谱绘图)
dt = t(2) - t(1);              % 时间间隔
f = (-Nt/2 : Nt/2 - 1) / (Nt * dt);  % 频率轴(Hz)
f_THz = f / 1e12;              % 转换为THz(便于显示)

%% 4. 结果可视化
fig = figure('Position', [100, 100, 1600, 1000]);
fig.Name = 'SPM引起的脉冲频谱展宽';

for p = 1:length(P0_list)
    P0 = P0_list(p);
    A = A_all{p};
    phi_spm = phi_spm_all{p};
    spec = spec_all{p};
    
    % 子图1：时域脉冲振幅(第一行)
    subplot(3, 3, p);
    plot(t / 1e-12, abs(A).^2, 'LineWidth', 2);
    xlabel('时间 (ps)', 'FontSize', 9);
    ylabel('光强 (arb. units)', 'FontSize', 9);
    title(['脉冲形状 (', num2str(P0), ' W)'], 'FontSize', 10);
    xlim([-50, 50]);
    grid on;
    box on;
    
    % 子图2：SPM相位(第二行)
    subplot(3, 3, p + 3);
    plot(t / 1e-12, phi_spm, 'r', 'LineWidth', 2);
    xlabel('时间 (ps)', 'FontSize', 9);
    ylabel('SPM相位 (rad)', 'FontSize', 9);
    title(['SPM相位分布', ' (', num2str(P0), ' W)'], 'FontSize', 10);
    xlim([-50, 50]);
    grid on;
    box on;
    
    % 子图3：频谱(第三行)
    subplot(3, 3, p + 6);
    plot(f_THz, spec, 'b', 'LineWidth', 2);
    xlabel('频率 (THz)', 'FontSize', 9);
    ylabel('频谱强度 (arb. units)', 'FontSize', 9);
    title(['频谱分布', ' (', num2str(P0), ' W)'], 'FontSize', 10);
    xlim([-10, 10]);  % 限制频率范围便于观察
    grid on;
    box on;
end

sgtitle('不同功率下的SPM效应与频谱展宽', 'FontSize', 14);

四、仿真结果分析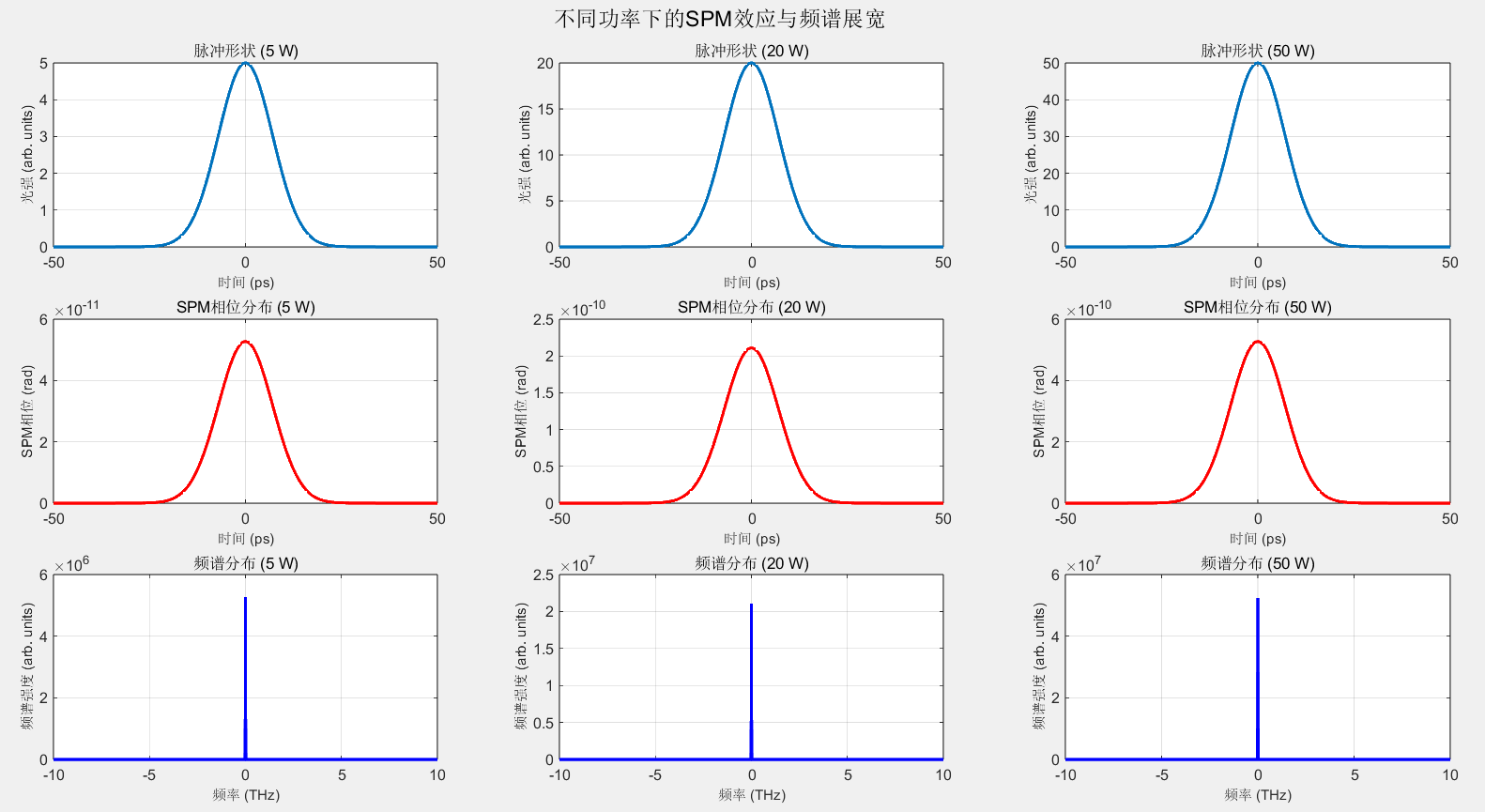

运行代码后，可观察到三组关键结果（对应不同脉冲功率）：

时域脉冲形状（第一行）：
- 所有脉冲均为高斯分布，功率越高，峰值光强越大
- 脉冲宽度未发生变化（简化模型中未考虑色散，仅体现 SPM 效应）
SPM 相位分布（第二行）：
- 相位随时间呈高斯分布（与光强分布一致），因 \(\phi_{\text{SPM}} \propto I(t)\)
- 功率越高，相位变化幅度越大（曲线峰值越高）
频谱展宽（第三行）：
- 低功率（5W）时，频谱接近高斯形状，展宽不明显
- 中功率（20W）时，频谱开始展宽，出现明显的旁瓣
- 高功率（50W）时，频谱大幅展宽，旁瓣增多，呈现典型的 SPM 频谱特征

核心规律：脉冲功率越高，SPM 相位变化越剧烈，频谱展宽越显著。这是因为相位随时间的变化率（\(\frac{d\phi}{dt}\)）直接决定了频率调制的强度，变化率越大，频谱展宽越明显。

五、扩展说明

色散的影响：实际中，光纤的色散会与 SPM 共同作用，导致更复杂的频谱演化（如孤子形成），可通过加入色散项进一步完善模型。
脉冲宽度的影响：更短的脉冲（如飞秒脉冲）光强更高，SPM 效应更显著，频谱展宽更明显。
材料选择：不同材料的克尔系数（\(n_2\)）不同，负\(n_2\)材料会产生反向相位调制，但同样会导致频谱展宽。

通过调整代码中的P0_list（功率）或L（传播距离），可直观观察不同条件下频谱展宽的变化，深入理解克尔效应在脉冲调制中的作用。