算法：二分算法类型题目总结---（含二分模版）

前言

这几天连着做了好几道二分题目，发现我们以前学习的那种最朴素的二分算法，在面临很多问题时候的解决效果不是很好，

于是，我去学习了一下优化版本的二分算法，发现，优化版本的二分算法，虽然更难控制，但是一旦明白了其中的逻辑，解决问题的效果比朴素二分算法要舒服很多，而且代码也都非常简短，大部分题目20多行就能解决。

这么好的方法，你确定不往下看嘛？

朴素二分算法

朴素的二分算法，每一个人都会，这里就用一道最经典的二分带大家复习一下朴素的二分算法吧。

题目：704. 二分查找

链接：704. 二分查找

思路

由于数组是升序数组，在有序数组中查找，第一反应就是二分算法，

每次查找直接排除掉一半不符合要修的数据

left = 0,right = nums.size() - 1;

while(left <= right)

mid = left + (right - left ) / 2;

if(target < nums[mid]) left = mid + 1;

else if(target > nums[mid]) right = mid - 1;

else return mid;

return -1;

具体代码

c 复制代码

    int search(vector<int>& nums, int target) {
        int l = 0,r = nums.size() - 1;
        int mid = 0;
        while(l <= r)
        {
            mid = l + (r-l + 1)/2;
            if(target < nums[mid])
            {
                r = mid - 1;
            }
            else if(target > nums[mid])
            {
                l = mid  + 1;
            }
            else return mid;
        }
        return l > r ? -1 : mid;
    }

优化版本的二分算法及模版

朴素的二分算法虽然能用，但是面对很多复杂问题的时候，调整起来太复杂了，而优化版本的二分算法能够适用于大部分场景，而且套路十分固定。

优化版本的二分算法原理

那么优化版本的二分算法究竟是什么样子的呢？究竟哪里优化了呢？

首先，我们来深入分析一下什么时候用二分算法，二分算法的二分是什么东西？

二分算法一定要要求数据有序吗？

都这么问了，那肯定不一定要求数据有序。

二分算法的核心是数据具有二段性！！！

也就是说数据有很明显的特征可以分成两个部分，

两个部分的特性不一样，就可以使用二分算法，

比如数据前一部分 > 0,后一部分 < 0，

前一部分递增，后一部分递减......

这些拥有二段性的数据都可以用二分算法来处理。

另外，还有一个小技巧，如果题目的数据量要求的时间复杂度大概是logN，那么百分百要用二分。

我们通过二分算法，可以将拥有二段性的数据的两种特性的边界数据找到，比如大于0到小于0的这个临界点，前一部分递增，后一部分递减的临界点。

优化版本的二分算法的模版

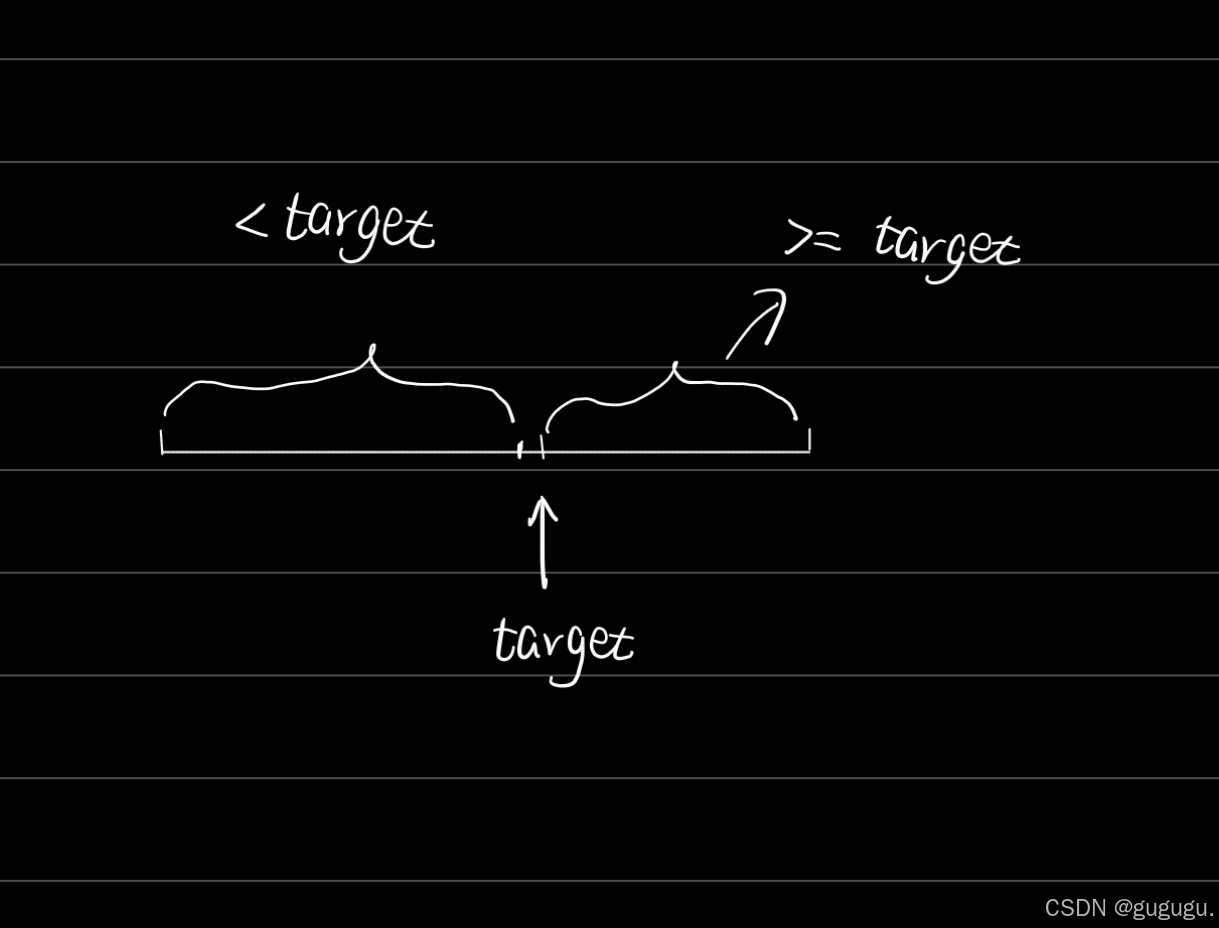
还是以上面的二分查找为例，要在一段有序数组中找到target，

数据的二段性是啥？显然是target左边的数据都小于target，右边的数据都大于等于target。

根据这个二段性，当我们获得到一个数据的时候，在判断的时候，只需要判断是在左边的区间还是右边的区间，

如果在左边的区间，就要想办法迅速跳出这个区间了，left = mid + 1;

如果在右边的区间，就要 right = mid，为什么不是mid - 1？因为mid处数据有可能就是target，我们要保证right不能跳出右边的区间。

另外，在循环条件处优化了，原来是left <= right，优化后left < right，

那么left == right就不判断了吗？当然要判断，只是，我们不在循环处判断，而是在循环外面判断。

如果我们让left <= right会怎么样？答案是会死循环。当 left==right && nums[mid] == target时，right = mid，就一直处于left == right == mid的情况，出不来循环。

第三处优化，原来我们的mid = left + (right - left) / 2;

现在我们mid需要根据实际情况来决定是mid = left + (right - left) / 2 还是 left + (right - left + 1) / 2 .

这两种mid有啥区别呢？区别就在于剩下最后两个元素的时候，取左边一个还是右边一个元素。

假设就剩两个元素 a 和 b ，下标left = 0，right = 1，那么两种情况下一个mid = 0，选了a，另一个mid = 1，选了b。

可是这两种mid实际应该用哪一个呢？

是这样的，我们在二段性划分区间的时候，

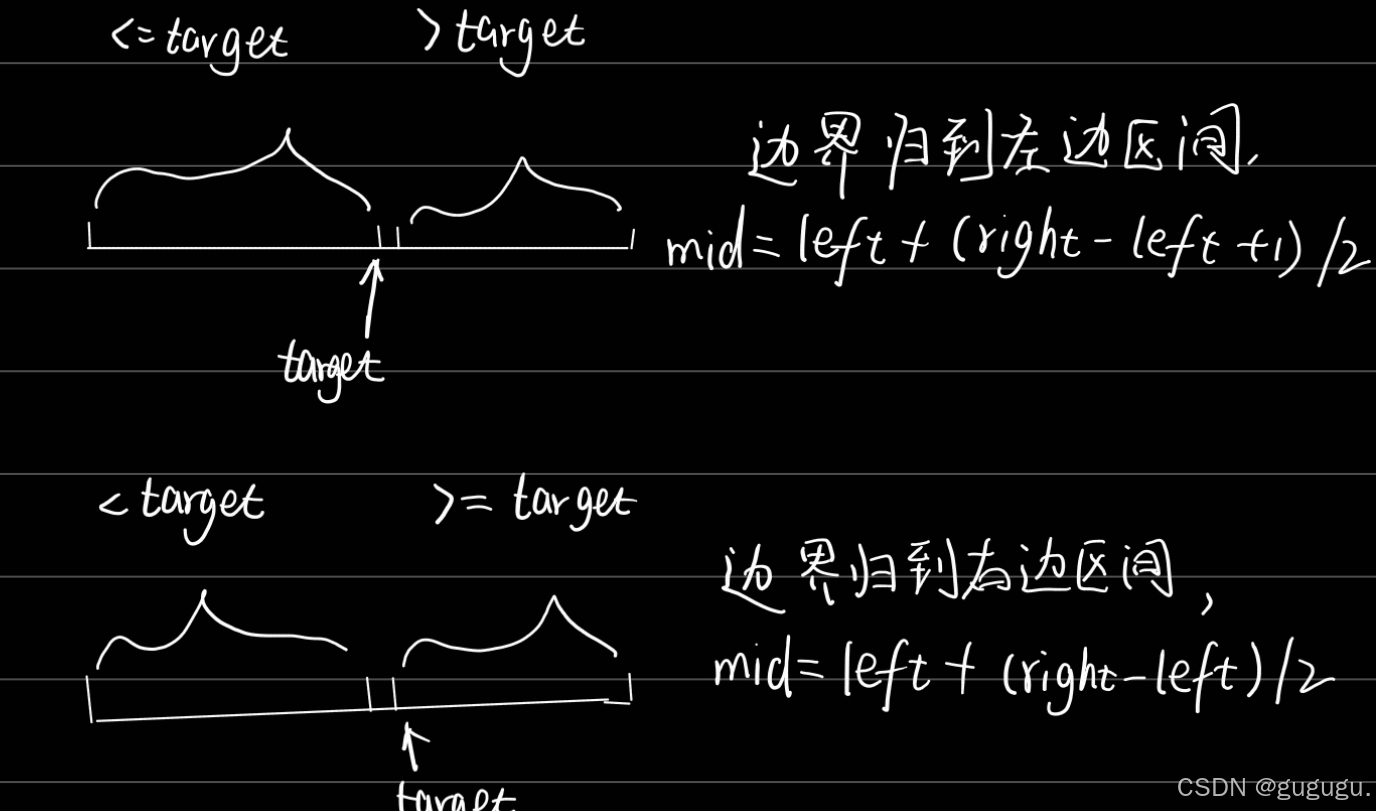
如果我们把边界归到了左边区间，就用mid = left + (right - left + 1) / 2，

如果我们把边界归到了右边区间，就用mid = left + (right - left) / 2。

当然，我们边界放到左右区间，在我们循环中判断的时候，也就不一样了，

边界在左边区间，就right = mid - 1，left = mid;

边界在右边区间，就left = mid + 1，right = mid;

模版代码

把边界归到右边区间

c 复制代码

int left = 0,right = nums.size() - 1;
int mid = 0;
while(left < right)
{
	mid = left + (right - left)/2;
	if(target > nums[mid]) left = mid + 1;
	else right = mid;
}

//后续判断

把边界归到左边区间

c 复制代码

int left = 0,right = nums.size() - 1;
int mid = 0;
while(left < right)
{
	mid = left + (right - left + 1)/2;
	if(target < nums[mid]) right = mid - 1;
	else left = mid;
}

//后续判断

细节

判断条件不一定是target < nums[mid]这种形式，判断条件应该是你的数据的二段性。

最后出循环了一定不是对mid进行判断，而是对left和right上的数据进行判断检查

二分算法练习

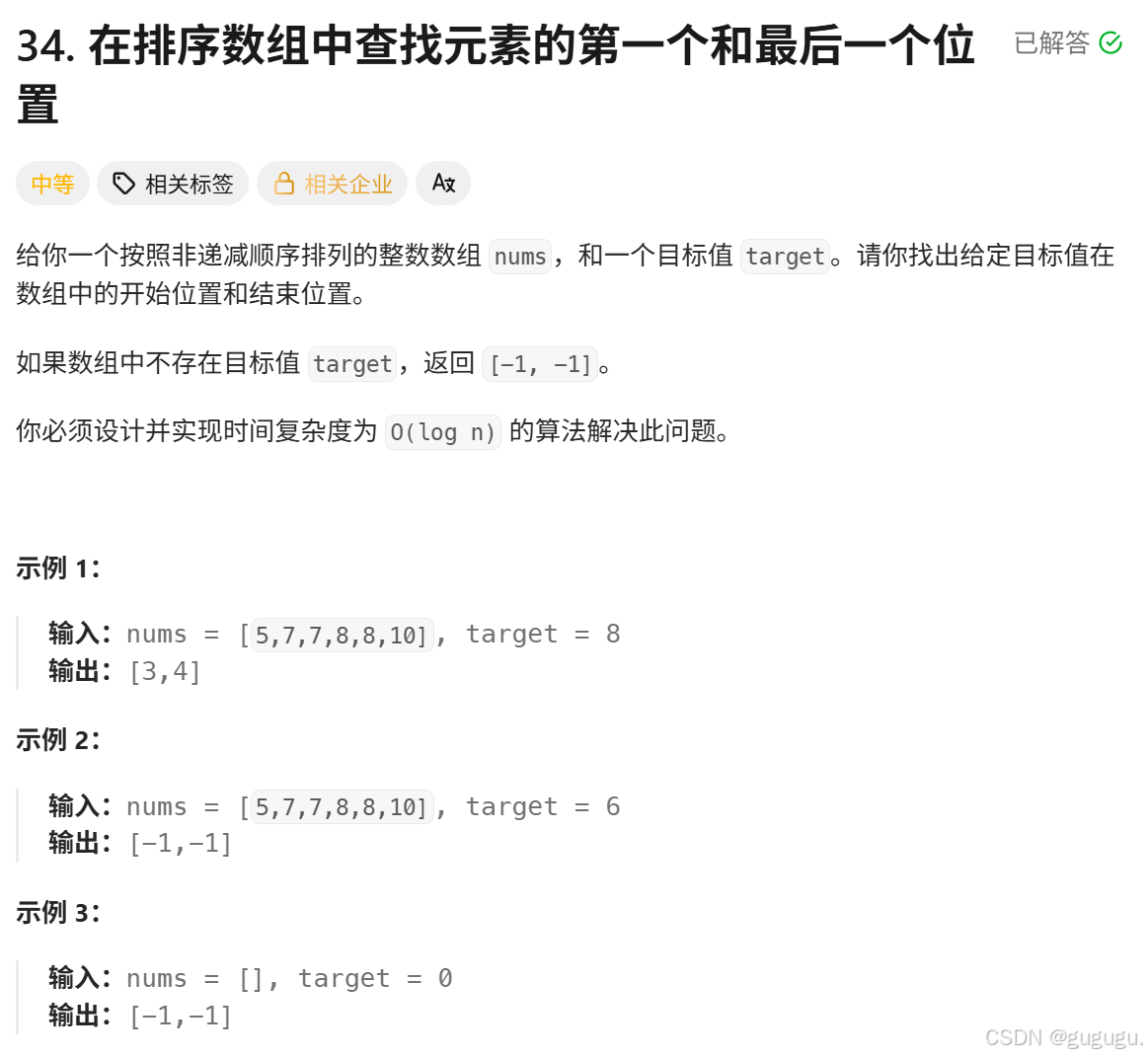
题目：34. 在排序数组中查找元素的第一个和最后一个位置

链接：34. 在排序数组中查找元素的第一个和最后一个位置

思路

这都非递减了，二段性太明显，二分秒了，

找第一个出现的位置的时候，二段性就是第一个出现的位置左边的数据全都 < target，右边全都 >= target，

找最后一个出现的位置的时候，二段性就是最后一个出现的位置右边的数据全员 > target，左边全都 <= target。

用两次二分算法就行了。

当然有一丁点坑，用完一次二分之后，left和right、mid记得重新初始化。

具体代码

c 复制代码

    vector<int> searchRange(vector<int>& nums, int target) {
        if(nums.size() == 0) return {-1,-1};
        int left = 0,right = nums.size() - 1;
        int mid = 0;

        //查找左端点
        while(left < right)
        {
            mid = left  + (right - left) / 2;
            if(nums[mid] < target) left = mid + 1;
            else right = mid;
        }

        int retl = left;
        left = 0,right = nums.size() - 1;
        mid = 0;

        //求右端点
        while(left < right)
        {
            mid = left + (right - left + 1) / 2;
            if(nums[mid] > target) right = mid - 1;
            else left = mid;

            cout << left << " " << right << endl;
        }
        int retr = right;

        if(nums[retl] == nums[retr] && nums[retl] == target) return {retl,retr};
        return {-1,-1};
    }

题目：35. 搜索插入位置

链接：35. 搜索插入位置

思路

这太简单了，就是基础二分，甚至朴素二分我估计也能做。

这道题把边界值划分到左右区间都能做，那么我们就假设划分到左边区间吧，

二段线就是target左侧全部 <= target，右边全都>target。

最后出循环了，进行判断的时候，

如果nums[left] >= target，return left；

如果nums[left] < target ，return left + 1

具体代码

c 复制代码

int searchInsert(vector<int>& nums, int target) {
    int left = 0,right = nums.size() - 1;

     int mid = 0;
     while(left < right)
     {
         mid = left + (right - left + 1) / 2;
         if(target < nums[mid]) right = mid - 1;
         else left = mid;
     }

     if(nums[left] == target) return left;
     if(nums[left] < target) return left + 1;
     //只要左边的数据比目标数据大，这个数据一定是刚好比target大，直接插在该位置
     if(nums[left] > target) return left;
}

题目：69. X的平方根

链接：69. X的平方根

这道题第一反应是遍历，一个个尝试，但是，显然复杂度O(N)，并不是很好。

所以得想一个办法，降低一下时间复杂度。

我们来尝试找一下二段性吧。

1 2 3 4 5 6 7......INT_MAX

诶，有序？我们是不是可以这么想，

假设平方根是mid，mid左侧的所有的数据的平方都 <= x，右侧的所有数据的平方都 > x，

二分算法不就来了吗？

right需要取INT_MAX吗？当然不需要，right只需要取2^16次方即可。

注意2^16次方的平方可能越界，所以在题目里面，可能会有一些地方需要转化成(long long)类型。

具体代码

c 复制代码

int mySqrt(int x) {
    int n = pow(2,16);
    int left = 0,right = n;
    int mid = 0;

    while(left < right)
    {
        mid = left + (right - left + 1) /2 ;
       if((long long)x < (long long)mid * (long long)mid) right = mid - 1;
       else left = mid;
    }

    //if(left * left <= x) return left;
    return left;
}

题目：852. 山脉数组的峰顶索引

链接：852. 山脉数组的峰顶索引

思路

这道题就开始有点不一样了，二段性就不是那么显而易见了，数据也不是有序数据了。

但是，依旧可以发现二段性。

山峰元素的左边的所有元素都是 nums[mid] > nums[mid - 1] && nums[mid] < nums[mid + 1]，

山峰元素的右边的所有元素都是 nums[mid] < nums[mid - 1] && nums[mid] > nums[mid + 1]，

至此，二分算法就很好写了，20来行。

细节：mid + 1，mid - 1，是不是要考虑越界啊！！！

所以，我们可以对0和n - 1的位置的元素特殊判断一下，提前判断是不是山峰索引。

具体代码

c 复制代码

int peakIndexInMountainArray(vector<int>& arr) {
    int left = 0,right = arr.size() - 1;
    int mid = 0;

    while(left < right)
    {
        mid = left + (right - left + 1) / 2;
        //特殊的处理一定要做
        //最右边一个山峰不可能是顶点，直接right - 1
        if(mid == arr.size() - 1 || (arr[mid] < arr[mid - 1] && arr[mid] > arr[mid + 1])) right = mid - 1;
        else left = mid;
    }
    return left;
}

题目：162. 寻找峰值

链接：162. 寻找峰值

思路

这题和上面的题目没有区别，题目说只需要返回任意一个山峰索引，就当时上面的那个题目一样做即可。

还是要注意0和n-1不要越界了，需要提前处理一下。

具体代码

c 复制代码

int findPeakElement(vector<int>& nums) {
    if(nums.size() == 1) return 0;

    int left = 0,right = nums.size() - 1;
    int mid =  0;
    while(left < right)
    {
        mid = left + (right - left + 1)/2;
        //这个题和前面那个山峰题不一样，这个题nums.size() 可以取 0 1 2，并且 -1和n都有效，需要特殊处理0和n-1
        if(mid == nums.size() - 1)
        {
            if(nums[mid] > nums[mid - 1])return mid;

            right = mid - 1;
            continue;
        }
        if(mid == 0 ) 
        {
            if(nums[0] > nums[1]) return 0;
            left = 1;

            continue;
        }

        if(nums[mid] > nums[mid + 1] && nums[mid] < nums[mid - 1]) right = mid - 1;
        else left = mid;
    }

    return left;
}

题目：153. 寻找旋转排序数组中的最小值

链接：153. 寻找旋转排序数组中的最小值

思路

这道题还真有点难度，二段性不是那么好想，

但是，如果你是一个做题喜欢画图的同学，这对你来说，二段性直接送到你眼前了呀。

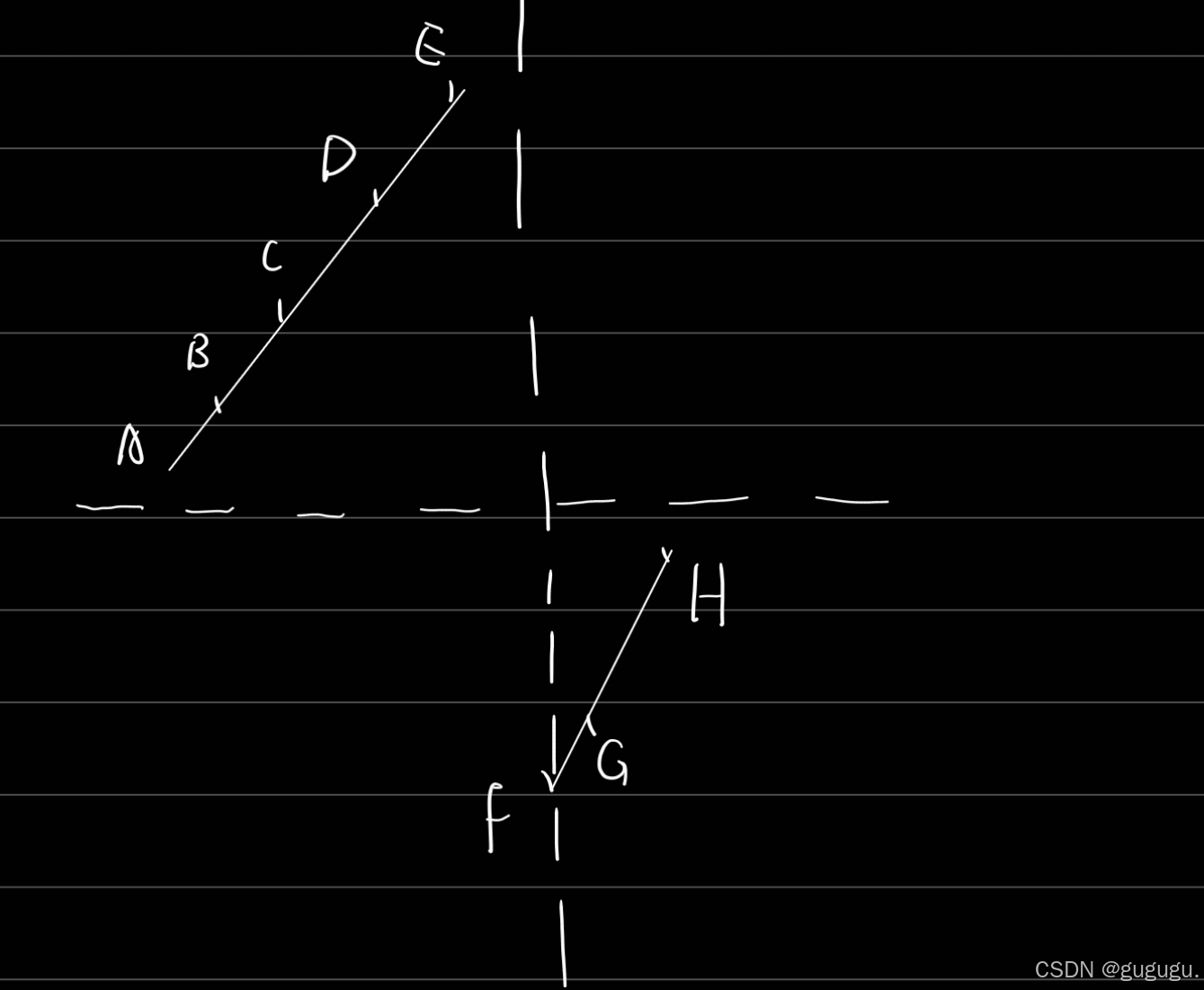
最小的元素的右边的所有的元素都 <= 最后一个元素，

最小的元素的左边的所有的元素都 > 最后一个元素。

二分算法这不就出来了吗？

具体代码

c 复制代码

int findMin(vector<int>& nums) {
    int left = 0,right = nums.size() - 1;

    int mid = 0;
    int t = nums[right];
    while(left < right)
    {
        mid = left + (right - left) / 2;
        
        //判断条件一定要根据实际情况来，不仅仅是有序数组的朴素二分
        if(nums[mid] > t) left = mid + 1;
        else right = mid;
    }

    return nums[left];
}

题目：LCR 173. 点名

链接：LCR 173. 点名

思路

这道题O(N)时间复杂度的算法太多了，我们使用一个O(logN)的算法来解决这个问题。

核心就是要找到二段性。

这道题目的二段性及其巧妙，大家可以学习一下。

假设缺失的同学叫做k，

我们发现：

k同学左边的所有的元素的学号都和下标相同，

k同学右边的所有的元素的学号都和下标不同（或者说比下标大1）。

二段性和下标联系上了，确实非常巧妙。

具体代码

c 复制代码

int takeAttendance(vector<int>& records) {
    //只有一个元素的时候要特殊处理一下
    if(records[0] == 1)return 0;

    int left = 0,right = records.size() - 1;
    int mid  = 0;

    while(left < right)
    {
        mid = left + (right - left + 1)/2;
        //非常巧妙的二段性划分，缺失同学前面的同学的学号等于下标
        if(records[mid] != mid) right = mid - 1;
        else left = mid;
    }

    return left + 1;
}