旋转位置编码RoPE：用旋转艺术，解开 Transformer 的位置之谜

位置编码RoPE：用旋转艺术，解开 Transformer 的位置之谜

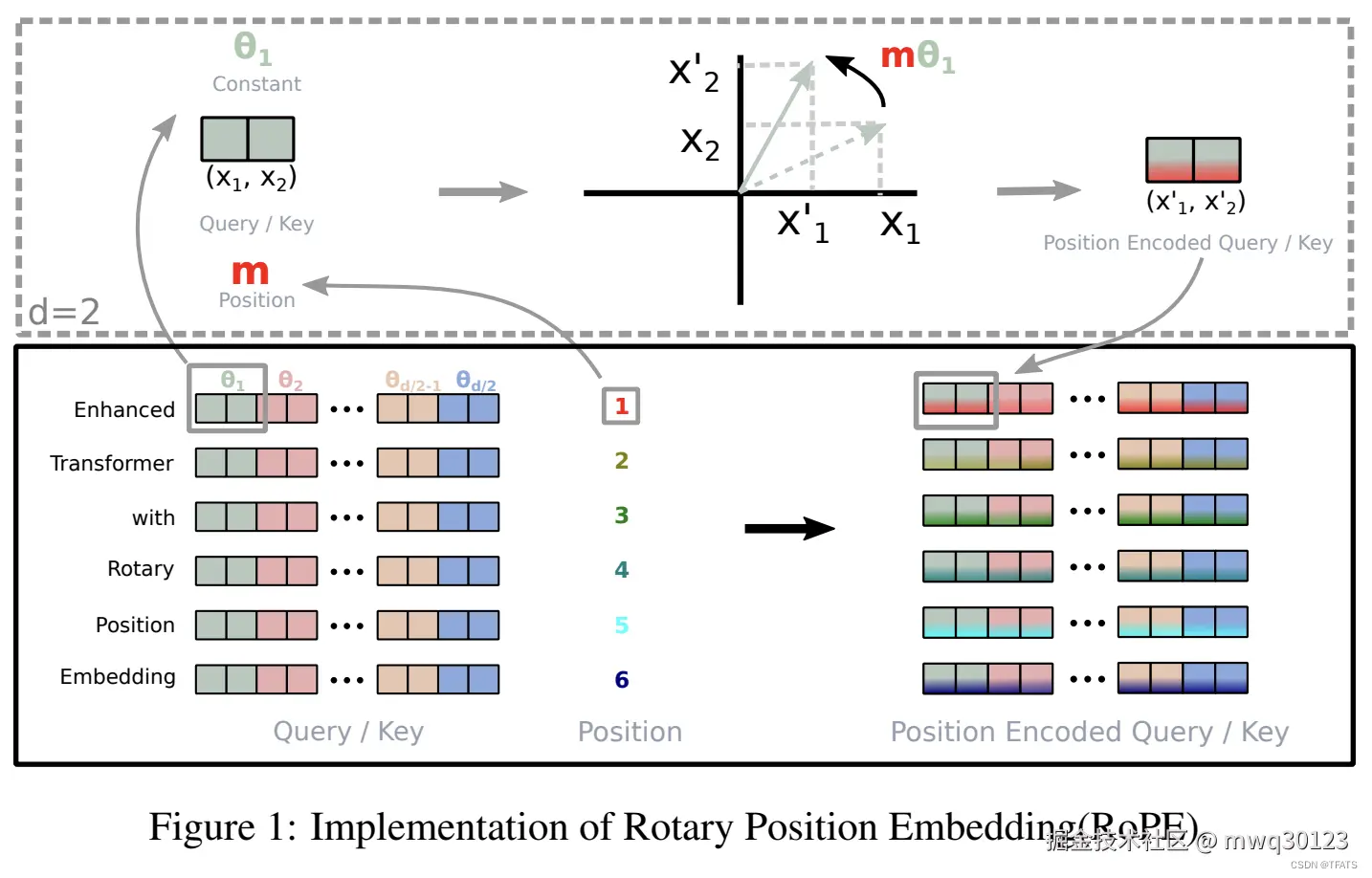在现代大型语言模型（LLM）的宏伟殿堂中，从 PaLM、Llama 到 GPT-NeoX，一个共同的基石在支撑着它们对序列顺序的理解：旋转位置编码 (Rotary Position Embedding, RoPE) 。

RoPE 不仅仅是另一种位置编码方案，它是一次优雅的数学推导的产物。它巧妙地以"绝对位置编码"的形式，实现了"相对位置编码"的特性，并顺便解决了传统位置编码与线性 Attention 之间的根本性冲突。

本文将深入探讨 RoPE 背后的数学原理、作者的思考出发点，以及它如何一步步从一个简洁的恒等式，演变为现代 LLM 的核心组件。

1. 问题的起点：我们到底想要什么？

Transformer 模型本身是置换不变 (Permutation-Invariant) 的，它无法感知序列的顺序。为了解决这个问题，我们需要注入位置信息。

原始 Transformer (APE)： 使用固定的 <math xmlns="http://www.w3.org/1998/Math/MathML"> sin ⁡ / cos ⁡ \sin/\cos </math>sin/cos 绝对位置编码 (APE) ，将其添加到词元嵌入中。这很管用，但模型必须"学会"如何从 <math xmlns="http://www.w3.org/1998/Math/MathML"> P E ( m ) PE(m) </math>PE(m) 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> P E ( n ) PE(n) </math>PE(n) 的组合中推断出相对位置 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( m − n ) (m-n) </math>(m−n)。
T5 (RPE)： 使用相对位置编码 (RPE) ，直接在 <math xmlns="http://www.w3.org/1998/Math/MathML"> N × N N \times N </math>N×N 的 Attention 矩阵上添加一个偏置项 <math xmlns="http://www.w3.org/1998/Math/MathML"> bias ( m − n ) \text{bias}(m-n) </math>bias(m−n)。这更直接，但带来了新的问题：
1. 外推性差： 在 2k 长度上训练的模型，无法推广到 4k。
2. 与线性 Attention 不兼容： 线性 Attention ( <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( N ) O(N) </math>O(N) ) 的核心就是避免构建 <math xmlns="http://www.w3.org/1998/Math/MathML"> N × N N \times N </math>N×N 矩阵。T5 的 RPE 必须操作这个矩阵，因此两者水火不容。

RoPE 的作者们另辟蹊径。他们提出了一个绝妙的"出发点"：

我们能否设计一个操作 <math xmlns="http://www.w3.org/1998/Math/MathML"> f f </math>f，它作用于向量 <math xmlns="http://www.w3.org/1998/Math/MathML"> q q </math>q 和它的绝对位置 <math xmlns="http://www.w3.org/1998/Math/MathML"> m m </math>m，使得 <math xmlns="http://www.w3.org/1998/Math/MathML"> q q </math>q 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> k k </math>k 在各自位置 <math xmlns="http://www.w3.org/1998/Math/MathML"> m , n m, n </math>m,n 上经过 <math xmlns="http://www.w3.org/1998/Math/MathML"> f f </math>f 操作后，它们的内积 <math xmlns="http://www.w3.org/1998/Math/MathML"> ⟨ f ( q , m ) , f ( k , n ) ⟩ \langle f(q,m), f(k,n) \rangle </math>⟨f(q,m),f(k,n)⟩ 只取决于 <math xmlns="http://www.w3.org/1998/Math/MathML"> q , k q, k </math>q,k 和它们的相对位置 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( m − n ) (m-n) </math>(m−n)？

用数学语言来描述这个目标，就是找到一个满足下列恒等式的解 <math xmlns="http://www.w3.org/1998/Math/MathML"> f f </math>f：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> ⟨ f ( q , m ) , f ( k , n ) ⟩ = g ( q , k , m − n ) \langle f(q,m), f(k,n) \rangle = g(q, k, m-n) </math>⟨f(q,m),f(k,n)⟩=g(q,k,m−n)

同时，为了让这个操作是一个"纯粹"的位置编码，我们希望它在 0 位置不改变原向量：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> f ( q , 0 ) = q f(q, 0) = q </math>f(q,0)=q

2. 核心推导：

从复数到 2D 旋转直接求解 <math xmlns="http://www.w3.org/1998/Math/MathML"> d d </math>d 维向量的 <math xmlns="http://www.w3.org/1998/Math/MathML"> f f </math>f 非常困难。作者巧妙地将问题简化：先在二维上求解 。二维向量可以被看作复数 <math xmlns="http://www.w3.org/1998/Math/MathML"> q ∈ C q \in \mathbb{C} </math>q∈C。二维向量的点积 <math xmlns="http://www.w3.org/1998/Math/MathML"> ⟨ q , k ⟩ \langle q, k \rangle </math>⟨q,k⟩ 等价于 <math xmlns="http://www.w3.org/1998/Math/MathML"> Re [ q k ∗ ] \text{Re}[qk^*] </math>Re[qk∗]（其中 <math xmlns="http://www.w3.org/1998/Math/MathML"> k ∗ k^* </math>k∗ 是 <math xmlns="http://www.w3.org/1998/Math/MathML"> k k </math>k 的复共轭）。我们的目标恒等式 <math xmlns="http://www.w3.org/1998/Math/MathML"> f f </math>f 变成了：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> Re [ f ( q , m ) f ∗ ( k , n ) ] = g ( q , k , m − n ) \text{Re}[ f(q,m) f^*(k,n) ] = g(q, k, m-n) </math>Re[f(q,m)f∗(k,n)]=g(q,k,m−n)

为了求解方便，我们假设一个更强的条件（后续只需取实部即可）：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> f ( q , m ) f ∗ ( k , n ) = g complex ( q , k , m − n ) f(q,m) f^*(k,n) = g_{\text{complex}}(q, k, m-n) </math>f(q,m)f∗(k,n)=gcomplex(q,k,m−n)

现在，我们将 <math xmlns="http://www.w3.org/1998/Math/MathML"> f f </math>f 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> g g </math>g 都写成复数的指数形式：

<math xmlns="http://www.w3.org/1998/Math/MathML"> f ( q , m ) = R f ( q , m ) e i Θ f ( q , m ) f(q,m) = R_f(q,m) e^{i\Theta_f(q,m)} </math>f(q,m)=Rf(q,m)eiΘf(q,m) ( <math xmlns="http://www.w3.org/1998/Math/MathML"> R f R_f </math>Rf 是模， <math xmlns="http://www.w3.org/1998/Math/MathML"> Θ f \Theta_f </math>Θf 是相位)

代入上式，得到：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> R f ( q , m ) R f ( k , n ) e i [ Θ f ( q , m ) − Θ f ( k , n ) ] = R g ( q , k , m − n ) e i Θ g ( q , k , m − n ) R_f(q,m)R_f(k,n) e^{i[\Theta_f(q,m) - \Theta_f(k,n)]} = R_g(q,k,m-n) e^{i\Theta_g(q,k,m-n)} </math>Rf(q,m)Rf(k,n)ei[Θf(q,m)−Θf(k,n)]=Rg(q,k,m−n)eiΘg(q,k,m−n)

这个复数等式必须模相等 且相位相等。

前置概念

在我们开始推导 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( q , m ) f ∗ ( k , n ) = g complex ( q , k , m − n ) f(q,m) f^*(k,n) = g_{\text{complex}}(q, k, m-n) </math>f(q,m)f∗(k,n)=gcomplex(q,k,m−n) 之前，需要先理解三个关键的复数工具：

1. 复共轭 (Complex Conjugate)

定义： 记为 <math xmlns="http://www.w3.org/1998/Math/MathML"> z ∗ z^* </math>z∗。如果 <math xmlns="http://www.w3.org/1998/Math/MathML"> z = a + b i z = a+bi </math>z=a+bi，则 <math xmlns="http://www.w3.org/1998/Math/MathML"> z ∗ = a − b i z^* = a-bi </math>z∗=a−bi。
指数形式： 如果 <math xmlns="http://www.w3.org/1998/Math/MathML"> z = R e i Θ z = Re^{i\Theta} </math>z=ReiΘ（ <math xmlns="http://www.w3.org/1998/Math/MathML"> R R </math>R 是模， <math xmlns="http://www.w3.org/1998/Math/MathML"> Θ \Theta </math>Θ 是相位），那么 <math xmlns="http://www.w3.org/1998/Math/MathML"> z ∗ = R e − i Θ z^* = Re^{-i\Theta} </math>z∗=Re−iΘ。
核心作用： 将相位取反。
为何重要：
1. 它是 RoPE 作者定义**复数内积（点积）**的基础： <math xmlns="http://www.w3.org/1998/Math/MathML"> ⟨ q , k ⟩ = Re [ q k ∗ ] \langle q, k \rangle = \text{Re}[qk^*] </math>⟨q,k⟩=Re[qk∗]。
2. 它是我们推导 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ∗ ( k , n ) f^*(k,n) </math>f∗(k,n) 的工具： <math xmlns="http://www.w3.org/1998/Math/MathML"> ( e i Θ ) ∗ = e − i Θ (e^{i\Theta})^* = e^{-i\Theta} </math>(eiΘ)∗=e−iΘ。

2. 模方程 (Modulus Equation)

定义： 这不是一个正式术语，而是我们求解复数等式 <math xmlns="http://www.w3.org/1998/Math/MathML"> Z 1 = Z 2 Z_1 = Z_2 </math>Z1=Z2 时，通过令等式两边的模（幅度 <math xmlns="http://www.w3.org/1998/Math/MathML"> R R </math>R）相等，得到的第一个实数方程。
原理： <math xmlns="http://www.w3.org/1998/Math/MathML"> Z 1 = Z 2 ⟹ ∥ Z 1 ∥ = ∥ Z 2 ∥ Z_1 = Z_2 \implies \|Z_1\| = \|Z_2\| </math>Z1=Z2⟹∥Z1∥=∥Z2∥。
为何重要： 在我们的推导中，它将 <math xmlns="http://www.w3.org/1998/Math/MathML"> f f </math>f 函数的"幅度"信息 <math xmlns="http://www.w3.org/1998/Math/MathML"> R f R_f </math>Rf 分离出来，帮助我们证明 <math xmlns="http://www.w3.org/1998/Math/MathML"> f f </math>f 必须是一个纯旋转操作（不改变向量长度）。

3. 相位方程 (Phase Equation)

定义： 类似地，这是求解 <math xmlns="http://www.w3.org/1998/Math/MathML"> Z 1 = Z 2 Z_1 = Z_2 </math>Z1=Z2 时，通过令等式两边的相位（角度 <math xmlns="http://www.w3.org/1998/Math/MathML"> Θ \Theta </math>Θ）相等，得到的第二个实数方程。
原理： <math xmlns="http://www.w3.org/1998/Math/MathML"> Z 1 = Z 2 ⟹ Angle ( Z 1 ) = Angle ( Z 2 ) Z_1 = Z_2 \implies \text{Angle}(Z_1) = \text{Angle}(Z_2) </math>Z1=Z2⟹Angle(Z1)=Angle(Z2)。
为何重要： 它将 <math xmlns="http://www.w3.org/1998/Math/MathML"> f f </math>f 函数的"角度"信息 <math xmlns="http://www.w3.org/1998/Math/MathML"> Θ f \Theta_f </math>Θf 分离出来。我们对这个方程的求解（ <math xmlns="http://www.w3.org/1998/Math/MathML"> ϕ ( m ) = m θ \phi(m) = m\theta </math>ϕ(m)=mθ），是 RoPE 旋转角度必须与位置 <math xmlns="http://www.w3.org/1998/Math/MathML"> m m </math>m 成线性关系的直接原因。

总结： 我们利用"复共轭"来构建初始的复数等式，然后使用"模方程"和"相位方程"这套方法，将这个复数等式拆解为两个独立的实数问题（一个关于长度，一个关于角度），从而分别求解。

我们就此得到了两个独立的实数方程：

(1) 模方程 (Magnitude Equation)

<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> R _ f ( q , m ) R _ f ( k , n ) = R _ g ( q , k , m − n ) R\_f(q,m)R\_f(k,n) = R\_g(q,k,m-n) </math>R_f(q,m)R_f(k,n)=R_g(q,k,m−n)

为了满足这个条件，最直接的解是 <math xmlns="http://www.w3.org/1998/Math/MathML"> R f ( q , m ) R_f(q,m) </math>Rf(q,m) 必须与 <math xmlns="http://www.w3.org/1998/Math/MathML"> m m </math>m 无关 ，即 <math xmlns="http://www.w3.org/1998/Math/MathML"> R f ( q , m ) = R f ( q ) R_f(q,m) = R_f(q) </math>Rf(q,m)=Rf(q)。应用初始条件 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( q , 0 ) = q f(q,0)=q </math>f(q,0)=q，我们得到 <math xmlns="http://www.w3.org/1998/Math/MathML"> R f ( q , 0 ) = ∥ q ∥ R_f(q,0) = \|q\| </math>Rf(q,0)=∥q∥。因此， <math xmlns="http://www.w3.org/1998/Math/MathML"> R f ( q , m ) = ∥ q ∥ R_f(q,m) = \|q\| </math>Rf(q,m)=∥q∥。

结论 1： <math xmlns="http://www.w3.org/1998/Math/MathML"> f f </math>f 操作不改变向量的长度 。它是一个纯粹的旋转操作。

(2) 相位方程 (Phase Equation)

<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> Θ f ( q , m ) − Θ f ( k , n ) = Θ g ( q , k , m − n ) \Theta_f(q,m) - \Theta_f(k,n) = \Theta_g(q,k,m-n) </math>Θf(q,m)−Θf(k,n)=Θg(q,k,m−n)

这是一个经典的函数方程。我们通过"变量分离"来求解：

令 <math xmlns="http://www.w3.org/1998/Math/MathML"> n = m n=m </math>n=m，得到 <math xmlns="http://www.w3.org/1998/Math/MathML"> Θ f ( q , m ) − Θ f ( k , m ) = Θ g ( q , k , 0 ) \Theta_f(q,m) - \Theta_f(k,m) = \Theta_g(q,k,0) </math>Θf(q,m)−Θf(k,m)=Θg(q,k,0)。
这个 <math xmlns="http://www.w3.org/1998/Math/MathML"> Θ g ( q , k , 0 ) \Theta_g(q,k,0) </math>Θg(q,k,0) 与 <math xmlns="http://www.w3.org/1998/Math/MathML"> m m </math>m 无关，所以它等于 <math xmlns="http://www.w3.org/1998/Math/MathML"> m = 0 m=0 </math>m=0 时的值： <math xmlns="http://www.w3.org/1998/Math/MathML"> Θ g ( q , k , 0 ) = Θ f ( q , 0 ) − Θ f ( k , 0 ) \Theta_g(q,k,0) = \Theta_f(q,0) - \Theta_f(k,0) </math>Θg(q,k,0)=Θf(q,0)−Θf(k,0)。
应用初始条件 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( q , 0 ) = q f(q,0)=q </math>f(q,0)=q，其相位 <math xmlns="http://www.w3.org/1998/Math/MathML"> Θ f ( q , 0 ) \Theta_f(q,0) </math>Θf(q,0) 就是 <math xmlns="http://www.w3.org/1998/Math/MathML"> q q </math>q 自己的幅角 <math xmlns="http://www.w3.org/1998/Math/MathML"> Θ ( q ) \Theta(q) </math>Θ(q)。
因此： <math xmlns="http://www.w3.org/1998/Math/MathML"> Θ f ( q , m ) − Θ f ( k , m ) = Θ ( q ) − Θ ( k ) \Theta_f(q,m) - \Theta_f(k,m) = \Theta(q) - \Theta(k) </math>Θf(q,m)−Θf(k,m)=Θ(q)−Θ(k)。
移项： <math xmlns="http://www.w3.org/1998/Math/MathML"> Θ f ( q , m ) − Θ ( q ) = Θ f ( k , m ) − Θ ( k ) \Theta_f(q,m) - \Theta(q) = \Theta_f(k,m) - \Theta(k) </math>Θf(q,m)−Θ(q)=Θf(k,m)−Θ(k)。
这个等式左边只与 <math xmlns="http://www.w3.org/1998/Math/MathML"> q , m q,m </math>q,m 相关，右边只与 <math xmlns="http://www.w3.org/1998/Math/MathML"> k , m k,m </math>k,m 相关。要使其对任意 <math xmlns="http://www.w3.org/1998/Math/MathML"> q , k q,k </math>q,k 成立，两边都必须等于一个只与 <math xmlns="http://www.w3.org/1998/Math/MathML"> m m </math>m 相关的函数 ，记为 <math xmlns="http://www.w3.org/1998/Math/MathML"> ϕ ( m ) \phi(m) </math>ϕ(m)。
<math xmlns="http://www.w3.org/1998/Math/MathML"> Θ f ( q , m ) = Θ ( q ) + ϕ ( m ) \Theta_f(q,m) = \Theta(q) + \phi(m) </math>Θf(q,m)=Θ(q)+ϕ(m)。又因 <math xmlns="http://www.w3.org/1998/Math/MathML"> Θ f ( q , 0 ) = Θ ( q ) \Theta_f(q,0) = \Theta(q) </math>Θf(q,0)=Θ(q)，可知 <math xmlns="http://www.w3.org/1998/Math/MathML"> ϕ ( 0 ) = 0 \phi(0) = 0 </math>ϕ(0)=0。
将 <math xmlns="http://www.w3.org/1998/Math/MathML"> Θ f ( q , m ) = Θ ( q ) + ϕ ( m ) \Theta_f(q,m) = \Theta(q) + \phi(m) </math>Θf(q,m)=Θ(q)+ϕ(m) 代回原始相位方程：

<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> [ Θ ( q ) + ϕ ( m ) ] − [ Θ ( k ) + ϕ ( n ) ] = Θ _ g ( q , k , m − n ) [\Theta(q) + \phi(m)] - [\Theta(k) + \phi(n)] = \Theta\_g(q,k,m-n) </math>[Θ(q)+ϕ(m)]−[Θ(k)+ϕ(n)]=Θ_g(q,k,m−n)
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> [ Θ ( q ) − Θ ( k ) ] + [ ϕ ( m ) − ϕ ( n ) ] = Θ g ( q , k , m − n ) [\Theta(q) - \Theta(k)] + [\phi(m) - \phi(n)] = \Theta_g(q,k,m-n) </math>[Θ(q)−Θ(k)]+[ϕ(m)−ϕ(n)]=Θg(q,k,m−n)

为使此式成立， <math xmlns="http://www.w3.org/1998/Math/MathML"> [ ϕ ( m ) − ϕ ( n ) ] [\phi(m) - \phi(n)] </math>[ϕ(m)−ϕ(n)] 必须是一个只关于 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( m − n ) (m-n) </math>(m−n) 的函数。唯一的线性解是 <math xmlns="http://www.w3.org/1998/Math/MathML"> ϕ ( m ) \phi(m) </math>ϕ(m) 是一个等差数列，即 <math xmlns="http://www.w3.org/1998/Math/MathML"> ϕ ( m ) = m θ \phi(m) = m\theta </math>ϕ(m)=mθ (公差为 <math xmlns="http://www.w3.org/1998/Math/MathML"> θ \theta </math>θ )。

结论 2： <math xmlns="http://www.w3.org/1998/Math/MathML"> f f </math>f 操作将 <math xmlns="http://www.w3.org/1998/Math/MathML"> q q </math>q 的原始相位 <math xmlns="http://www.w3.org/1998/Math/MathML"> Θ ( q ) \Theta(q) </math>Θ(q) 增加了 <math xmlns="http://www.w3.org/1998/Math/MathML"> m θ m\theta </math>mθ。

(3) 最终解综合模和相位：

<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> f ( q , m ) = R f ( q , m ) e i Θ f ( q , m ) f(q,m) = R_f(q,m) e^{i\Theta_f(q,m)} </math>f(q,m)=Rf(q,m)eiΘf(q,m)
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> f ( q , m ) = ∣ q ∣ e i ( Θ ( q ) + m θ ) f(q,m) = |q| e^{i(\Theta(q) + m\theta)} </math>f(q,m)=∣q∣ei(Θ(q)+mθ)
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> f ( q , m ) = ( ∣ q ∣ e i Θ ( q ) ) ⋅ ( e i m θ ) f(q,m) = (|q| e^{i\Theta(q)}) \cdot (e^{im\theta}) </math>f(q,m)=(∣q∣eiΘ(q))⋅(eimθ)
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> f ( q , m ) = q e i m θ f(q,m) = q e^{im\theta} </math>f(q,m)=qeimθ

这个解极其简洁： <math xmlns="http://www.w3.org/1998/Math/MathML"> f f </math>f 操作就是将二维向量 <math xmlns="http://www.w3.org/1998/Math/MathML"> q q </math>q 旋转 <math xmlns="http://www.w3.org/1998/Math/MathML"> m θ m\theta </math>mθ 角度。

我们来验证一下它是否满足我们的初衷：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> </math>
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> = Re [ q e i m θ ⋅ k ∗ e − i n θ ] = Re [ ( q k ∗ ) e i ( m − n ) θ ] = \text{Re}[ q e^{im\theta} \cdot k^* e^{-in\theta} ] = \text{Re}[ (qk^*) e^{i(m-n)\theta} ] </math>=Re[qeimθ⋅k∗e−inθ]=Re[(qk∗)ei(m−n)θ]

这个结果只依赖于 <math xmlns="http://www.w3.org/1998/Math/MathML"> q , k q, k </math>q,k 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( m − n ) (m-n) </math>(m−n)。推导成功！

3. 推广到 <math xmlns="http://www.w3.org/1998/Math/MathML"> d d </math>d 维：线性叠加的威力

我们已经成功找到了 2D（复数）情况下的解。那么，如何将其推广到 Transformer 使用的 <math xmlns="http://www.w3.org/1998/Math/MathML"> d d </math>d 维向量（例如 <math xmlns="http://www.w3.org/1998/Math/MathML"> d = 512 d=512 </math>d=512）上呢？

关键就在于您提到的**"内积满足线性叠加性"**。

<math xmlns="http://www.w3.org/1998/Math/MathML"> d d </math>d 维向量 <math xmlns="http://www.w3.org/1998/Math/MathML"> q \mathbf{q} </math>q 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> k \mathbf{k} </math>k 的内积 <math xmlns="http://www.w3.org/1998/Math/MathML"> ⟨ q , k ⟩ \langle \mathbf{q}, \mathbf{k} \rangle </math>⟨q,k⟩ 定义为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> ⟨ q , k ⟩ = ∑ j = 0 d − 1 q j k j \langle \mathbf{q}, \mathbf{k} \rangle = \sum_{j=0}^{d-1} q_j k_j </math>⟨q,k⟩=∑j=0d−1qjkj

我们可以将这个 <math xmlns="http://www.w3.org/1998/Math/MathML"> d d </math>d 维向量**强行"切分"**成 <math xmlns="http://www.w3.org/1998/Math/MathML"> d / 2 d/2 </math>d/2 组 2D 向量：

<math xmlns="http://www.w3.org/1998/Math/MathML"> q ( 0 ) = ( q 0 , q 1 ) \mathbf{q}^{(0)} = (q_0, q_1) </math>q(0)=(q0,q1)
<math xmlns="http://www.w3.org/1998/Math/MathML"> q ( 1 ) = ( q 2 , q 3 ) \mathbf{q}^{(1)} = (q_2, q_3) </math>q(1)=(q2,q3)
...
<math xmlns="http://www.w3.org/1998/Math/MathML"> q ( i ) = ( q 2 i , q 2 i + 1 ) \mathbf{q}^{(i)} = (q_{2i}, q_{2i+1}) </math>q(i)=(q2i,q2i+1)

<math xmlns="http://www.w3.org/1998/Math/MathML"> d d </math>d 维内积 <math xmlns="http://www.w3.org/1998/Math/MathML"> ⟨ q , k ⟩ \langle \mathbf{q}, \mathbf{k} \rangle </math>⟨q,k⟩ 就可以被拆解为这些 2D 组的内积之和：

<math xmlns="http://www.w3.org/1998/Math/MathML"> ⟨ q , k ⟩ = ( q 0 k 0 + q 1 k 1 ) ⏟ ⟨ q ( 0 ) , k ( 0 ) ⟩ + ( q 2 k 2 + q 3 k 3 ) ⏟ ⟨ q ( 1 ) , k ( 1 ) ⟩ + ⋯ + ( q d − 2 k d − 2 + q d − 1 k d − 1 ) ⏟ ⟨ q ( d / 2 − 1 ) , k ( d / 2 − 1 ) ⟩ \langle \mathbf{q}, \mathbf{k} \rangle = \underbrace{(q_0k_0 + q_1k_1)}{\langle \mathbf{q}^{(0)}, \mathbf{k}^{(0)} \rangle} + \underbrace{(q_2k_2 + q_3k_3)}{\langle \mathbf{q}^{(1)}, \mathbf{k}^{(1)} \rangle} + \dots + \underbrace{(q_{d-2}k_{d-2} + q_{d-1}k_{d-1})}_{\langle \mathbf{q}^{(d/2-1)}, \mathbf{k}^{(d/2-1)} \rangle} </math>⟨q,k⟩=⟨q(0),k(0)⟩ (q0k0+q1k1)+⟨q(1),k(1)⟩ (q2k2+q3k3)+⋯+⟨q(d/2−1),k(d/2−1)⟩ (qd−2kd−2+qd−1kd−1)

<math xmlns="http://www.w3.org/1998/Math/MathML"> ⟨ q , k ⟩ = ∑ i = 0 d / 2 − 1 ⟨ q ( i ) , k ( i ) ⟩ \langle \mathbf{q}, \mathbf{k} \rangle = \sum_{i=0}^{d/2-1} \langle \mathbf{q}^{(i)}, \mathbf{k}^{(i)} \rangle </math>⟨q,k⟩=∑i=0d/2−1⟨q(i),k(i)⟩

RoPE 的 <math xmlns="http://www.w3.org/1998/Math/MathML"> d d </math>d 维实现正是利用了这一点：我们不对 <math xmlns="http://www.w3.org/1998/Math/MathML"> d d </math>d 维向量 <math xmlns="http://www.w3.org/1998/Math/MathML"> q \mathbf{q} </math>q 进行一次 <math xmlns="http://www.w3.org/1998/Math/MathML"> d d </math>d 维旋转，而是将其拆分为 <math xmlns="http://www.w3.org/1998/Math/MathML"> d / 2 d/2 </math>d/2 个 2D 向量，然后对每一组 2D 向量独立地应用我们推导出的 2D 旋转。

<math xmlns="http://www.w3.org/1998/Math/MathML"> d d </math>d 维的 RoPE 变换 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( q , m ) f(\mathbf{q}, m) </math>f(q,m) 就是一个块对角矩阵 (Block Diagonal Matrix) <math xmlns="http://www.w3.org/1998/Math/MathML"> R m \mathbf{R}_m </math>Rm 与 <math xmlns="http://www.w3.org/1998/Math/MathML"> q \mathbf{q} </math>q 相乘。矩阵的每个 <math xmlns="http://www.w3.org/1998/Math/MathML"> 2 × 2 2 \times 2 </math>2×2 的对角块，都是一个 2D 旋转矩阵，形式与您的(10)式一致（只是 <math xmlns="http://www.w3.org/1998/Math/MathML"> θ \theta </math>θ 根据不同维度 <math xmlns="http://www.w3.org/1998/Math/MathML"> i i </math>i 而变化，记为 <math xmlns="http://www.w3.org/1998/Math/MathML"> θ i \theta_i </math>θi）：

<math xmlns="http://www.w3.org/1998/Math/MathML"> f ( q , m ) = R m q = ( cos ⁡ m θ 0 sin ⁡ m θ 0 0 0 ⋯ 0 0 − sin ⁡ m θ 0 cos ⁡ m θ 0 0 0 ⋯ 0 0 0 0 cos ⁡ m θ 1 sin ⁡ m θ 1 ⋯ 0 0 0 0 − sin ⁡ m θ 1 cos ⁡ m θ 1 ⋯ 0 0 ⋮ ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ 0 0 0 0 ⋯ cos ⁡ m θ d / 2 − 1 sin ⁡ m θ d / 2 − 1 0 0 0 0 ⋯ − sin ⁡ m θ d / 2 − 1 cos ⁡ m θ d / 2 − 1 ) ( q 0 q 1 q 2 q 3 ⋮ q d − 2 q d − 1 ) f(\mathbf{q}, m) = \mathbf{R}m \mathbf{q} = \begin{pmatrix} \cos m\theta_0 & \sin m\theta_0 & 0 & 0 & \cdots & 0 & 0 \\ -\sin m\theta_0 & \cos m\theta_0 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cos m\theta_1 & \sin m\theta_1 & \cdots & 0 & 0 \\ 0 & 0 & -\sin m\theta_1 & \cos m\theta_1 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \cos m\theta{d/2-1} & \sin m\theta_{d/2-1} \\ 0 & 0 & 0 & 0 & \cdots & -\sin m\theta_{d/2-1} & \cos m\theta_{d/2-1} \end{pmatrix} \begin{pmatrix} q_0 \\ q_1 \\ q_2 \\ q_3 \\ \vdots \\ q_{d-2} \\ q_{d-1} \end{pmatrix} </math>f(q,m)=Rmq= cosmθ0−sinmθ000⋮00sinmθ0cosmθ000⋮0000cosmθ1−sinmθ1⋮0000sinmθ1cosmθ1⋮00⋯⋯⋯⋯⋱⋯⋯0000⋮cosmθd/2−1−sinmθd/2−10000⋮sinmθd/2−1cosmθd/2−1 q0q1q2q3⋮qd−2qd−1

这个矩阵 <math xmlns="http://www.w3.org/1998/Math/MathML"> R m \mathbf{R}_m </math>Rm 在做什么？

它将 <math xmlns="http://www.w3.org/1998/Math/MathML"> q 0 , q 1 q_0, q_1 </math>q0,q1 作为一个 2D 向量，并将其旋转 <math xmlns="http://www.w3.org/1998/Math/MathML"> − m θ 0 -m\theta_0 </math>−mθ0 角度。
它将 <math xmlns="http://www.w3.org/1998/Math/MathML"> q 2 , q 3 q_2, q_3 </math>q2,q3 作为一个 2D 向量，并将其旋转 <math xmlns="http://www.w3.org/1998/Math/MathML"> − m θ 1 -m\theta_1 </math>−mθ1 角度。
...
它将 <math xmlns="http://www.w3.org/1998/Math/MathML"> q d − 2 , q d − 1 q_{d-2}, q_{d-1} </math>qd−2,qd−1 作为一个 2D 向量，并将其旋转 <math xmlns="http://www.w3.org/1998/Math/MathML"> − m θ d / 2 − 1 -m\theta_{d/2-1} </math>−mθd/2−1 角度。

（注：在实践中，不同组 <math xmlns="http://www.w3.org/1998/Math/MathML"> i i </math>i 使用不同的旋转频率 <math xmlns="http://www.w3.org/1998/Math/MathML"> θ i = 1000 0 − 2 i / d \theta_i = 10000^{-2i/d} </math>θi=10000−2i/d，这与原始 Transformer 的 <math xmlns="http://www.w3.org/1998/Math/MathML"> sin ⁡ / cos ⁡ \sin/\cos </math>sin/cos 编码的波长设计一致。）

最终结论：

当我们计算 <math xmlns="http://www.w3.org/1998/Math/MathML"> d d </math>d 维的内积 <math xmlns="http://www.w3.org/1998/Math/MathML"> ⟨ f ( q , m ) , f ( k , n ) ⟩ \langle f(\mathbf{q},m), f(\mathbf{k},n) \rangle </math>⟨f(q,m),f(k,n)⟩ 时，根据内积的线性叠加性：

<math xmlns="http://www.w3.org/1998/Math/MathML"> ⟨ f ( q , m ) , f ( k , n ) ⟩ = ⟨ R m q , R n k ⟩ = ∑ i = 0 d / 2 − 1 ⟨ ( R m q ) ( i ) , ( R n k ) ( i ) ⟩ \langle f(\mathbf{q},m), f(\mathbf{k},n) \rangle = \langle \mathbf{R}_m \mathbf{q}, \mathbf{R}n \mathbf{k} \rangle = \sum{i=0}^{d/2-1} \langle (\mathbf{R}_m \mathbf{q})^{(i)}, (\mathbf{R}_n \mathbf{k})^{(i)} \rangle </math>⟨f(q,m),f(k,n)⟩=⟨Rmq,Rnk⟩=∑i=0d/2−1⟨(Rmq)(i),(Rnk)(i)⟩

右侧的每一项 <math xmlns="http://www.w3.org/1998/Math/MathML"> ⟨ ⋅ ⟩ i \langle \cdot \rangle_i </math>⟨⋅⟩i 都是 2D RoPE，它们都只依赖于 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( m − n ) (m-n) </math>(m−n) 。因此，它们的总和也必然只依赖于 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( m − n ) (m-n) </math>(m−n)。

我们成功地将 2D 的解，通过"分而治之"和"线性叠加"的方式，推广到了任意 <math xmlns="http://www.w3.org/1998/Math/MathML"> d d </math>d 维。

4. RoPE 解决了什么核心问题？

RoPE 以其优雅的数学形式，一举解决了多个难题：

实现了"绝对操作，相对结果"：

它通过 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( q , m ) f(\mathbf{q}, m) </math>f(q,m)（绝对位置 <math xmlns="http://www.w3.org/1998/Math/MathML"> m m </math>m）和 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( k , n ) f(\mathbf{k}, n) </math>f(k,n)（绝对位置 <math xmlns="http://www.w3.org/1998/Math/MathML"> n n </math>n）的独立操作，实现了 <math xmlns="http://www.w3.org/1998/Math/MathML"> ⟨ ⋅ , ⋅ ⟩ \langle \cdot, \cdot \rangle </math>⟨⋅,⋅⟩ 结果只依赖 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( m − n ) (m-n) </math>(m−n) 的相对特性。
与线性 Attention 完美兼容（杀手级特性）：

这是 RoPE 最大的工程胜利。传统 RPE (T5-bias) 需要操作 <math xmlns="http://www.w3.org/1998/Math/MathML"> N × N N \times N </math>N×N 矩阵，无法用于线性 Attention。

RoPE 不操作 <math xmlns="http://www.w3.org/1998/Math/MathML"> N × N N \times N </math>N×N 矩阵。它在 Attention 运算之前，分别"预处理" <math xmlns="http://www.w3.org/1998/Math/MathML"> Q \mathbf{Q} </math>Q 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> K \mathbf{K} </math>K 矩阵（ <math xmlns="http://www.w3.org/1998/Math/MathML"> Q ~ = R m Q , K ~ = R n K \tilde{\mathbf{Q}} = \mathbf{R}_m \mathbf{Q}, \tilde{\mathbf{K}} = \mathbf{R}_n \mathbf{K} </math>Q~=RmQ,K~=RnK）。

线性 Attention 的 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( N ) O(N) </math>O(N) 运算 <math xmlns="http://www.w3.org/1998/Math/MathML"> Q ~ ( K ~ T V ) \tilde{\mathbf{Q}} (\tilde{\mathbf{K}}^T \mathbf{V}) </math>Q~(K~TV) 可以照常进行，它甚至"不知道" <math xmlns="http://www.w3.org/1998/Math/MathML"> Q ~ , K ~ \tilde{\mathbf{Q}}, \tilde{\mathbf{K}} </math>Q~,K~ 已经被旋转过，但相对位置信息已经蕴含在内积中了。
良好的外推性（后续改进的基础）：

由于 <math xmlns="http://www.w3.org/1998/Math/MathML"> ⟨ q ~ , k ~ ⟩ = Re [ ( q k ∗ ) e i ( m − n ) θ ] \langle \tilde{q}, \tilde{k} \rangle = \text{Re}[ (qk^*) e^{i(m-n)\theta} ] </math>⟨q~,k~⟩=Re[(qk∗)ei(m−n)θ]，随着相对距离 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( m − n ) (m-n) </math>(m−n) 的增加，Attention 得分会自然地振荡和衰减。这提供了一种比 APE 更自然的"距离越远、关注越少"的归纳偏置。虽然它本身的外推并非完美，但它为后来的 NTK-Aware 和 YaRN 等改进方法提供了坚实的理论基础。

总结

RoPE 是那种在学术界和工业界都"大获全胜"的罕见技术。它从一个简单而深刻的数学恒等式出发，通过严谨的复数推导，最终得到了一个极其简洁的物理解释------旋转。这个简单的旋转操作，不仅统一了绝对位置和相对位置的优点，还解开了 RPE 与线性 Attention 之间的死结，为当今万亿参数模型的上下文扩展打开了大门。