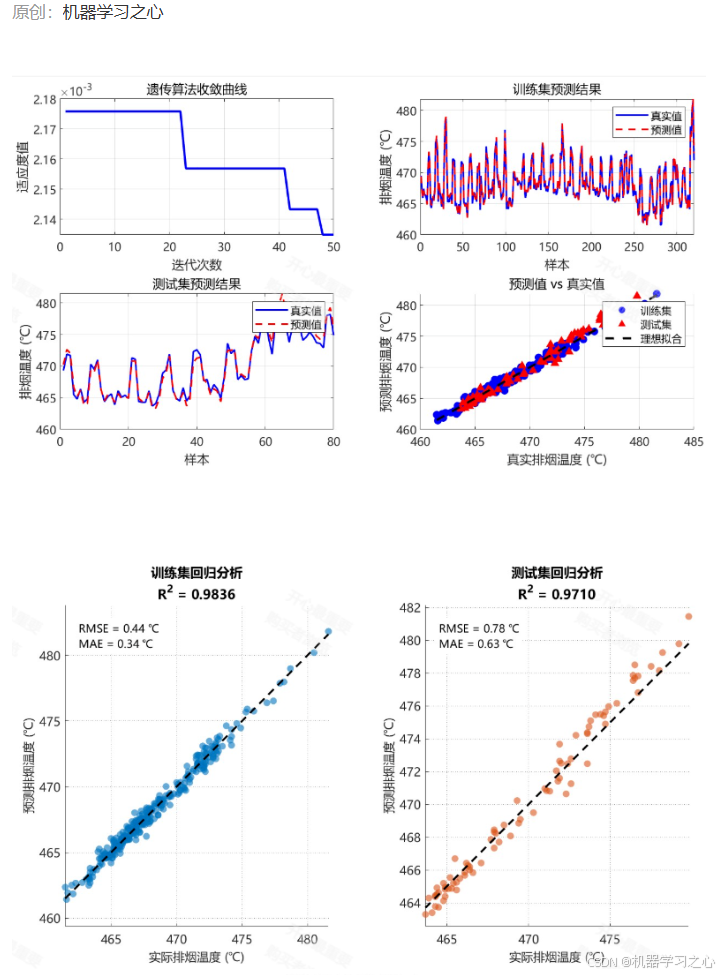
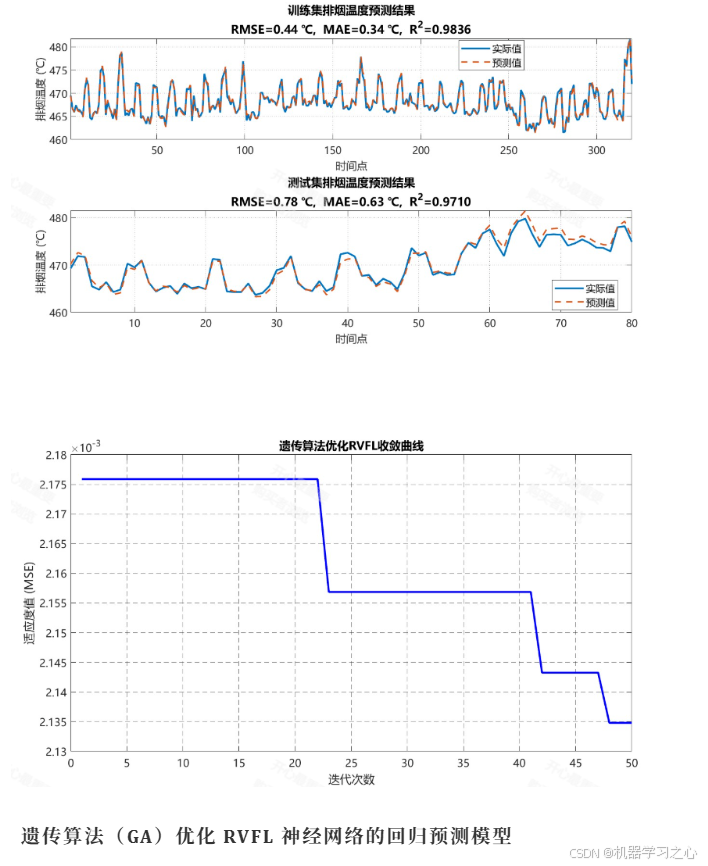
1. 为什么要把 GA 与 RVFL 结合?
| 关键点 | 说明 | 参考 |
|---|---|---|
| RVFL 的优势 | 单隐层结构、随机生成输入‑隐藏层权重与偏置、输出层采用最小二乘求解,训练速度极快,适合大规模回归。 | [[1]] |
| RVFL 的不足 | 随机权重可能导致非最优解,隐藏层节点数、激活函数、正则化系数等超参数对预测精度影响显著。 | [[2]] |
| GA 的作用 | 通过全局搜索避免局部最优,能够同时优化 权重、偏置、隐藏层节点数、激活函数参数、正则化系数 等,提升模型的鲁棒性与泛化能力。 | [[3]][[4]] |
| 实际验证 | 多篇最新研究表明 GA‑RVFL 在油田产量预测、医学影像诊断、金融时间序列等回归任务上显著优于原始 RVFL、BP‑NN、GWO‑RVFL 等基准。 | [[5]][[6]][[7]] |
关键实现细节(参考文献)
- 适应度函数 :多数工作直接使用 RMSE 作为 GA 的目标函数,亦可加入 MAE、R² 的加权组合,以兼顾误差分布与解释度[[8]][[9]]。
- 种群规模 & 代数 :常见设置为 pop = 50‑100 ,max gen = 50‑200,在实际实验中发现 100 代即可收敛,进一步提升代数对精度提升有限[[10]]。
- 交叉/变异率 :交叉率 0.8、变异率 0.1‑0.2 为常用组合,变异采用 高斯噪声 对连续参数(权重、偏置)进行微调,对离散参数(节点数)使用 均匀随机 重新抽样[[11]]。
- 正则化 :在最小二乘求解 β 时加入 L2 正则化 λ,GA 同时搜索 λ 的最优取值,避免过拟合
2. MATLAB示例代码片段
matlab
%--- 1. 数据准备 -------------------------------------------------
X = normalize(trainX); % 输入特征归一化
Y = trainY; % 目标变量
%--- 2. GA 参数设置 ------------------------------------------------
popSize = 80; % 种群规模
maxGen = 120; % 最大代数
pc = 0.8; % 交叉概率
pm = 0.15; % 变异概率
lb = [5, -1, -1, 1e-5]; % [隐藏层节点数, 权重下限, 偏置下限, 正则化λ]
ub = [200, 1, 1, 1]; % 上界
% 适应度函数:返回 RMSE(越小越好)
fitnessFcn = @(ind) ga_rvfl_fitness(ind, X, Y);
%--- 3. 运行 GA -------------------------------------------------
options = optimoptions('ga','PopulationSize',popSize,...
'MaxGenerations',maxGen,'CrossoverFraction',pc,...
'MutationRate',pm,'Display','iter');
[bestInd, bestFit] = ga(fitnessFcn,4,[],[],[],[],lb,ub,[],options);
%--- 4. 用最优个体构建最终 RVFL -------------------------------
L = round(bestInd(1)); % 隐藏层节点数
W = bestInd(2) * rand(L,size(X,2)); % 随机权重(已缩放)
b = bestInd(3) * rand(L,1); % 随机偏置
lambda = bestInd(4); % L2 正则化系数
H = tanh(X*W' + b'); % 隐藏层特征(可换激活函数)
Z = [X, H']; % 增强特征
beta = (Z'*Z + lambda*eye(size(Z,2))) \ (Z'*Y); % 最小二乘求解
%--- 5. 测试集评估 ------------------------------------------------
Ypred = [testX, tanh(testX*W' + b')] * beta;
RMSE = sqrt(mean((Ypred - testY).^2));
fprintf('GA‑RVFL Test RMSE = %.4f\n',RMSE);3. 常见调参技巧与经验总结
| 经验 | 说明 |
|---|---|
| 节点数与数据维度的比例 | 当特征维度 d 较大时,隐藏层节点数 L ≈ 2‑5 × d 能兼顾表达能力与计算成本[[17]]。 |
| 激活函数的选择 | tanh、sigmoid、relu 均可;若使用 模糊激活函数 (如文献中提出的 s‑fuzzy),可在 GA 中把模糊参数加入基因,进一步提升非线性拟合能力[[18]]。 |
| 正则化 λ 的搜索范围 | 建议在 [10⁻⁵, 1] 对数空间均匀抽样,防止过拟合且不影响收敛速度[[19]]。 |
| 精英保留 | 每代保留 前 5% 最佳个体,可显著加速收敛,避免优秀解被随机变异抹掉[[20]]。 |
| 终止准则 | 除最大代数外,可加入 适应度变化 < 1e‑4 连续 10 代即停止,节约计算资源。 |
4. 小结
- RVFL 本身因随机权重训练快、结构简洁而适合作为基准回归模型。
- 遗传算法 能在全局搜索空间中同步优化 权重、偏置、隐藏层节点数、正则化系数、激活函数参数,显著提升模型的预测精度与鲁棒性。
- 实践中 种群规模 50‑100、代数 50‑150、交叉 0.8、变异 0.1‑0.2 是常用且效果稳健的配置。
- 多篇 2023‑2025 年最新研究(油田产量、医学影像、金融时间序列等)均验证了 GA‑RVFL 在回归任务上的 优势显著。
- 代码实现相对直接:先用 GA 搜索超参数,再用最小二乘求解输出层权重,最后在全量训练集上重新训练得到最终模型。