算法题（Python）数组篇 | 6.区间和

一、题目描述
二、思路

一、题目描述

给定一个整数数组Array，请计算该数组在每个指定区间内元素的总和。

输入描述：

复制代码

第一行输入为整数数组Array的长度n，接下来n行，每行一个整数，表示数组的元素。
随后的输入为需要计算总和的区间下标：a，b(b >= a)，直至结束

输出描述：

复制代码

输出每个指定区间内元素的总和。

二、思路

首先看到本题时的最直观的想法是暴力解法，即：给一个区间，把这个区间的和都累加一遍即可，代码如下：

python 复制代码

if __name__ == "__main__":
    n = int(input())
    nums = [0] * n
    for i in range(0, n):
        nums[i] = int(input())
    while True:
        try:
            a, b = map(int, input().split())
            sum = 0
            for i in range(a, b + 1):
                sum += nums[i]
            print(sum)
        except:
            break

但是提交代码后，存在超时问题：

举一个极端的例子，如果我查询m次，每次查询的范围都是从0到n-1，那么该算法的时间复杂度是 O ( n × m ) O(n \times m) O(n×m)。如果查询次数非常大的话，这个时间复杂度会很高。

因此，通过此题引入前缀和概念，前缀和的思想是重复利用计算过的子数组之和，从而降低区间查询需要累加计算的次数。

前缀和在涉及计算区间和的问题时非常有用！

示例：假设我们要统计nums[i]这个数组上的区间和。我们先做累加，即p[i]表示下标0到i的nums[i]累加之和。

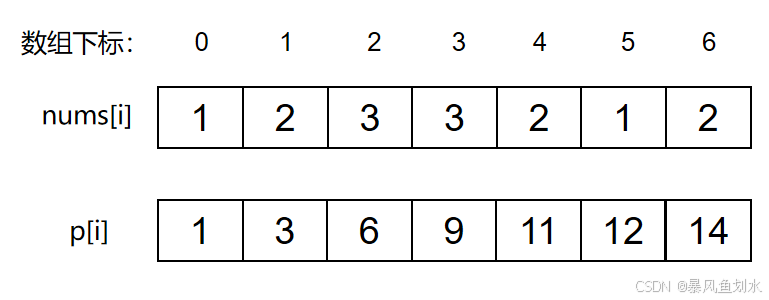
如果，我们想统计nums数组上下标2到下标5之间的累加和，是不是用p[5]-p[1]即可：

p[1] = nums[0] + nums[1]

p[5] = nums[0] + nums[1] + nums[2] + nums[3] + nums[4] + nums[5]

p[5] - p[1] = nums[2] + nums[3] + nums[4] + nums[5]

如下图所示，p[5] - p[1]就是绿色部分的区间和，而p数组是之前计算好的累加和，所以后面每次求区间和之后，只需要 O ( 1 ) O(1) O(1)操作。

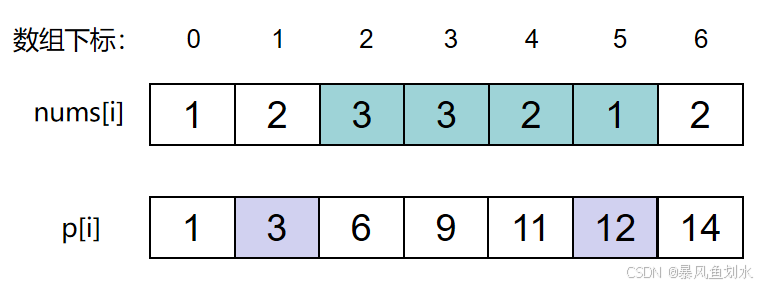
本题代码如下：

python 复制代码

if __name__ == "__main__":
    n = int(input())
    nums = [0] * n
    p = [0] * n
    presum = 0
    for i in range(0, n):
        nums[i] = int(input())
        presum += nums[i]
        p[i] = presum
    while True:
        try:
            sum = 0
            a, b = map(int, input().split())
            if a == 0:
                sum = p[b]
            else:
                sum = p[b] - p[a - 1]
            print(sum)
        except:
            break