【数据结构】双向链表

1.双向链表

1.1 概念与结构

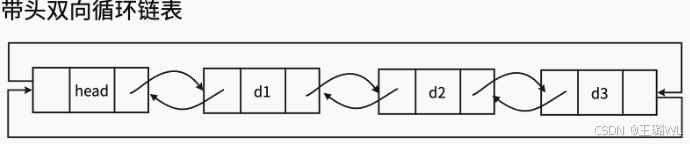
1.2 实现双向链表

c 复制代码

//List.h 
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef int LTDataType; 
typedef struct ListNode 
{ 
    struct ListNode* next; //指针保存下⼀个结点的地址 
    struct ListNode* prev; //指针保存前⼀个结点的地址 
    LTDataType data; 
}LTNode; 

//第一种方法：要修改头结点，要用LTNode** pphead接收
//void LTInit(LTNode** pphead); 
//第二种方法：不需要二级指针
LTNode* LTInit(); 

//第一种销毁方法：
//void LTDestroy(LTNode** pphead);
//第二种方法：
void LTDestroy(LTNode* phead);

//创建
LTNode* LTBuyNode(LTDataType x);

//打印
void LTPrint(LTNode* phead);
//判断链表是否为空
bool LTEmpty(LTNode* phead); 

//在双向链表中，增删改查都不会改变哨兵位结点，所以用LTNode* phead
void LTPushBack(LTNode* phead, LTDataType x); 
//尾删
void LTPopBack(LTNode* phead); 

//头插
void LTPushFront(LTNode* phead, LTDataType x); 
//头删
void LTPopFront(LTNode* phead); 

//在pos位置之后插⼊数据
void LTInsert(LTNode* pos, LTDataType x); 
//删除pos结点
void LTErase(LTNode* pos); 
//查找
LTNode *LTFind(LTNode* phead,LTDataType x);

c 复制代码

//List.c
#include"List.h"

LTNode* LTBuyNode(LTDataType x)
{
    LTNode* newnode=(LTNode*)malloc(sizeof(LTNode));
    if(newnode==NULL)
    {
        perror("malloc");
        exit(1);
    }
    newnode->data=x;
    newnode->next=newnode->prev=newnode;//空指针也可以用这句代码
    return newnode;
}

//void LTInit(LTNode** pphead)
//{
//    *pphead=LTBuyNode(-1);
//}
LTNode* LTInit()
{
    LTNode* phead=LTBuyNode(-1);
    return phead;
}

//void LTDestroy(LTNode** pphead)
//{
    //先从第一个有效结点开始删除
//   LTNode* pcur=(*pphead)->next;
//    while(pcur!=*pphead)
//    {
//        LTNode* next=pcur->next;//先把下一个结点存起来
//        free(pcur);
//        pcur=next;
//    }
    //销毁头结点
//    free(*pphead);
//    *pphead=NULL;
//}
void LTDestroy(LTNode* phead)
{
    LTNode* pcur=(phead)->next;
    while(pcur!=phead)
    {
        LTNode* next=pcur->next;//先把下一个结点存起来
        free(pcur);
        pcur=next;
    }
    free(phead);
    phead=NULL;
}



void LTPushBack(LTNode* phead, LTDataType x)
{
    assert(phead);
    LTNode* newnode=LTBuyNode(x);
    //phead->prev是原本的尾结点
    //先修改newnode，不会改变原链表
    newnode->prev=phead->prev;
    newnode->next=phead;
    //先连后断
    phead->prev->next=newnode;
    phead->prev=newnode;
}

//插入在第一个有效的结点的前面
void LTPushFront(LTNode* phead, LTDataType x)
{
    LTNode* newnode=LTBuyNode(x);
    //先修改newnode，不会改变原链表
    newnode->next=phead->next;
    newnode->prev=phead;
    phead->next->prev=newnode;
    phead->next=newnode;
}

bool LTEmpty(LTNode* phead)
{
    assert(phead);
    return phead->next==phead;//链表的next指向自己就返回
}

//尾删
//头删和尾删要确保链表不为空
void LTPopBack(LTNode* phead)
{
  	assert(!LTEmpty(phead));
    LTNode* del=phead->prev;
    del->prev->next=phead;
    prev->prev=del->prev;
    free(del);
    del=NULL;
}
//打印
void LTPrint(LTNode* phead)
{
    LTNode* pcur=phead->next;
    //只要pcur->next!=phead
    while(pcur->next!=phead)
    {
        printf("%d->",pcur->data);
        pcur=pcur->next;
    }
    printf("\n");
}
//删除第一个有效结点
void LTPopFront(LTNode* phead)
{
    assert(!LTEmpty(phead));
    LTNode*del=phead->next;
    del->next->prev=phead;
    phead->next=del->next;
    free(del);
    del=NULL;
}
//查找
LTNode *LTFind(LTNode* phead,LTDataType x)
{
    assert(phead);
    LTNode* pcur=phead->next;
    while(pcur!=head)
    {
        if(pcur->data==x)
            return pcur;
        pcur=pcur->next;
    }
    //未找到
    return NULL;
}

//在pos之后插入一个值为x的结点
void LTInsert(LTNode* pos, LTDataType x)
{
    assert(pos);
    LTNode* newnode=LTBuyNode(x);
    //先修改newnode，不会改变原链表
    newnode->prev=pos;
    newnode->next=pos->next;
    //先连再断
    pos->next->prev=newnode;
    pos->next=newnode;
}

void LTErase(LTNode* pos)
{
    assert(pos);
    pos->prev->next=pos->next;
    pos->next->prev=pos->prev; 
    free(pos);
    pos=NULL;
}

c 复制代码

//test.c
#include"List.h"
void test01()
{
    //LTNode* plist=NULL;
    //LTInit(&plist);
    LTNode* plist=LTInit();
    
    //尾插
    LTPushBack(plist,1);
    LTPushBack(plist,2);
    LTPushBack(plist,3);
    LTPushBack(plist,4);
    
    //头插
    LTPushFront(plist,1);
    LTPushFront(plist,2);
    LTPushFront(plist,3);
    LTPushFront(plist,4);
    
    //尾删
    LTPopBack(plist);
    LTPrint(plist);
    LTPopBack(plist);
    LTPrint(plist);
    LTPopBack(plist);
    LTPrint(plist);
    
    //头删
    LTPopFront(plist);
    LTPrint(plist);
    LTPopFront(plist);
    LTPrint(plist);
    LTPopFront(plist);
    LTPrint(plist);
    
    //查找
    LTNode* pos=LTFind(plist,2);
    if(pos)
        printf("找到了\n");
    else
        printf("未找到\n");
    
    //在pos之后插入100
    LTInsert(pos,100);
    LTPrint(plist);
    //删除pos结点
    LTErase(pos);
    LTPrint(plist);
    
    //销毁
    //LTDesTroy(&plist);
    LTDesTroy(plist);
    plist=NULL;
}
int main()
{
    test01();
    return 0;
}

2.顺序表与链表的分析

不同点	顺序表	链表（单链表）
存储空间上	物理上⼀定连续	逻辑上连续，但物理上不⼀定连续
随机访问	⽀持O(1)	不⽀持：O(N)
任意位置插⼊或者删除元素	可能需要搬移元素，效率低O(N)	在指定位置之后插入或删除元素只需修改指针指向
插⼊	动态顺序表，空间不够时需要扩容和空间浪费	没有容量的概念，按需申请释放，不存在空间浪费
应⽤场景	元素⾼效存储+频繁访问	任意位置⾼效插⼊和删除