深入浅出蓝桥杯：算法基础概念与实战应用（一）基础算法(上)

铭哥的编程日记2025-11-11 8:06

蓝桥杯通关秘籍（一）：算法基础篇：基础算法(上)

文章目录

  • 蓝桥杯通关秘籍（一）：算法基础篇：基础算法(上)
  • 一、模拟
    • [1.1 多项式输出](#1.1 多项式输出)
    • [1.2 蛇形⽅阵](#1.2 蛇形⽅阵)
    • [1.3 字符串的展开](#1.3 字符串的展开)
  • 二、高精度
    • [2.1 ⾼精度加法](#2.1 ⾼精度加法)
    • [2.2 ⾼精度减法](#2.2 ⾼精度减法)
    • [2.3 ⾼精度乘法](#2.3 ⾼精度乘法)
    • [2.4 ⾼精度除法](#2.4 ⾼精度除法)
  • 三、枚举
  • [3.1 普通枚举](#3.1 普通枚举)
    • [3.1.1 铺地毯](#3.1.1 铺地毯)
    • [3.1.2 回⽂⽇期](#3.1.2 回⽂⽇期)
    • [3.1.3 扫雷](#3.1.3 扫雷)
  • [3.2 ⼆进制枚举](#3.2 ⼆进制枚举)
    • [3.2.1 ⼦集](#3.2.1 ⼦集)
    • [3.2.2 费解的开关](#3.2.2 费解的开关)
    • [3.2.3 Even Parity](#3.2.3 Even Parity)
  • 四、前缀和
    • [4.1 ⼀维前缀和](#4.1 ⼀维前缀和)
    • [4.2 最⼤⼦段和](#4.2 最⼤⼦段和)
    • [4.3 ⼆维前缀和](#4.3 ⼆维前缀和)
    • [4.4 激光炸弹](#4.4 激光炸弹)
  • 五、差分
    • [5.1 ⼀维差分](#5.1 ⼀维差分)
    • [5.2 海底⾼铁](#5.2 海底⾼铁)
    • [5.3 ⼆维差分](#5.3 ⼆维差分)
    • [5.4 地毯](#5.4 地毯)
  • 六、双指针
    • [6.1 唯⼀的雪花](#6.1 唯⼀的雪花)
    • [6.2 逛画展](#6.2 逛画展)
    • [6.3 字符串](#6.3 字符串)
    • [6.4 丢⼿绢](#6.4 丢⼿绢)
  • 七、二分算法
  • [7.1 ⼆分查找](#7.1 ⼆分查找)
    • [7.1.1 ⽜可乐和魔法封印](#7.1.1 ⽜可乐和魔法封印)
    • [7.1.2 A-B 数对](#7.1.2 A-B 数对)
    • [7.1.3 烦恼的⾼考志愿](#7.1.3 烦恼的⾼考志愿)
  • [7.2 ⼆分答案](#7.2 ⼆分答案)
    • [7.2.1 ⽊材加⼯](#7.2.1 ⽊材加⼯)
    • [7.2.2 砍树](#7.2.2 砍树)
    • [7.2.3 跳⽯头](#7.2.3 跳⽯头)
  • 整体源代码

一、模拟

1.1 多项式输出

牛客网链接



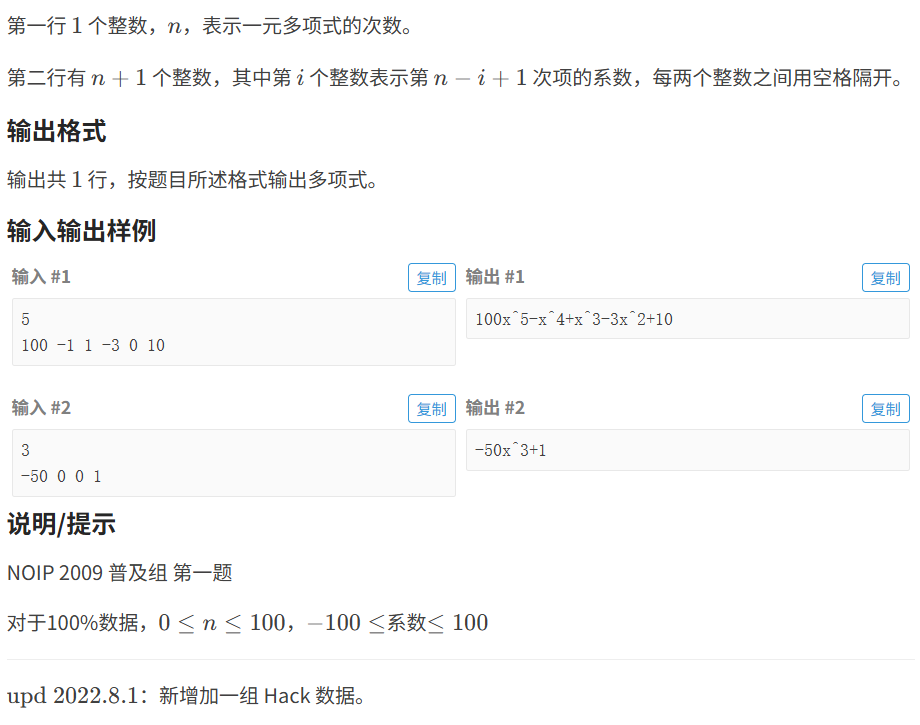
代码如下（示例）：

c 复制代码 
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
    int n; cin >> n;
    // 循环次数
    for (int i = n; i >= 0; i--)
    {
        int a; cin >> a;
        if (a == 0) continue; // 处理系数为 0 的情况
        // 1. 符号
        if (a < 0) cout << '-';
        else
        {
            if (i != n) cout << '+';
        }
        // 2. 数字
        a = abs(a);
        if (a != 1 || (a == 1 && i == 0)) cout << a;
        // 3. 次数
        if (i == 0) continue;
        else if (i == 1) cout << 'x';
        else cout << "x^" << i;
    }
    return 0;
}

1.2 蛇形⽅阵

牛客网链接

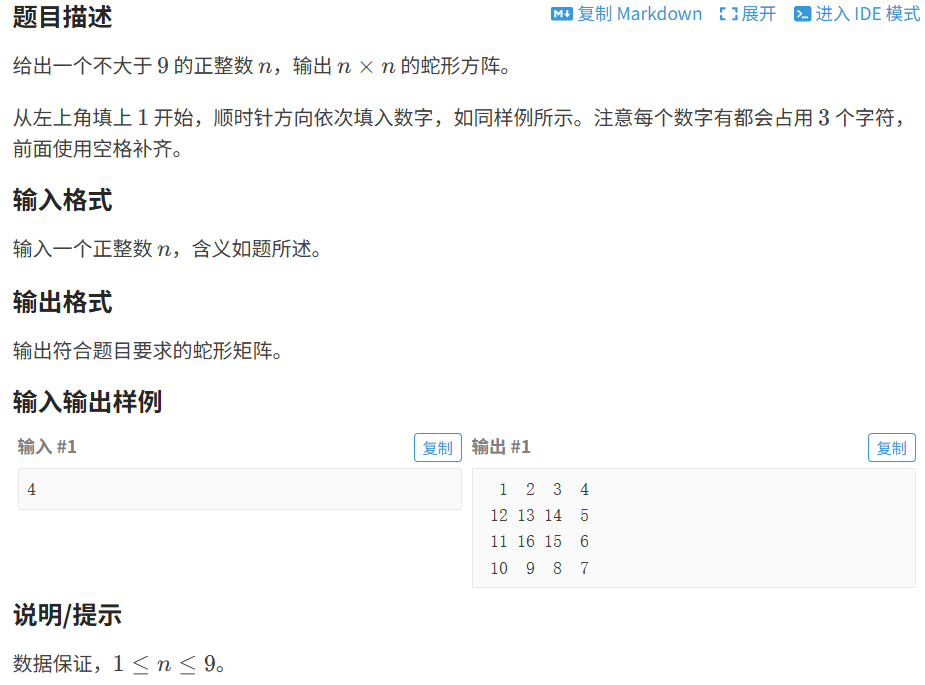
代码如下（示例）：

c 复制代码 
#include<iostream>
using namespace std;

int dx[4] = { 0 , 1 , 0 , -1 };
int dy[4] = { 1 , 0 ,-1 ,  0 };
const int N = 15;
int arr[N][N];

int main()
{
	int n; cin >> n;
	int cnt = 1;
	int pos = 0;
	int x = 1, y = 1;
	while (cnt <= n * n)
	{
		arr[x][y] = cnt;
		int a = x + dx[pos], b = y + dy[pos];
		if (a < 1 || a > n || b < 1 || b > n || arr[a][b])
		{
			pos = (pos + 1) % 4;
			a = x + dx[pos], b = y + dy[pos];
		}
		x = a, y = b;
		cnt++;
	}
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			printf("%3d", arr[i][j]);
		}
		puts("");
	}
}

1.3 字符串的展开

牛客网链接


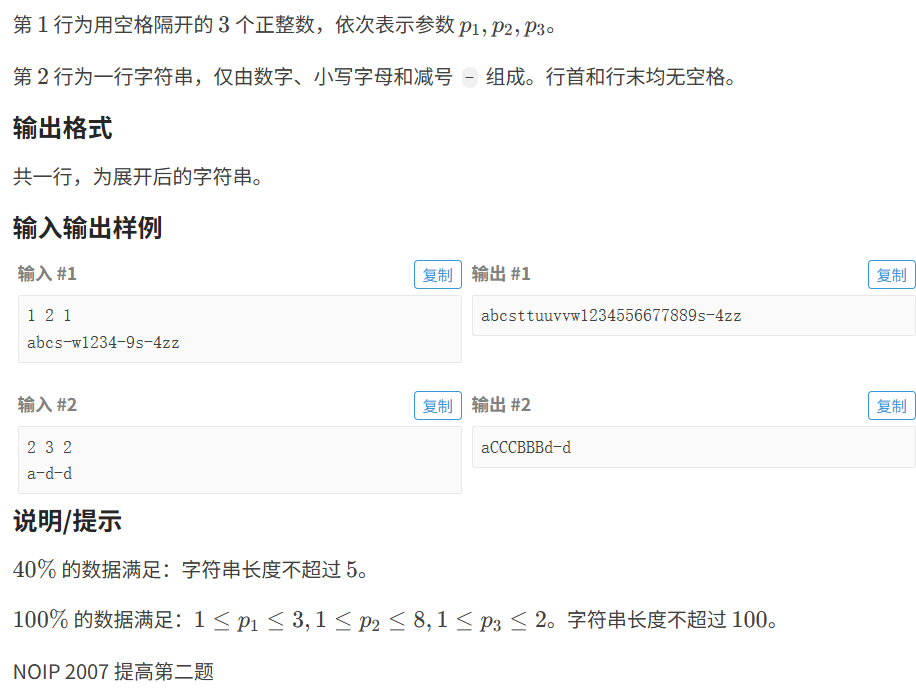
代码如下（示例）：

c 复制代码 
#include <iostream>
#include<string>
#include <algorithm>
using namespace std;
int p1, p2, p3, n;
string s;
string ret;
// 判断是否是数字字符
bool isdig(char ch)
{
	return ch >= '0' && ch <= '9';
}
// 判断是否是⼩写字⺟
bool islet(char ch)
{
	return ch >= 'a' && ch <= 'z';
}
// 把 [left, right] 之间的字符展开
// left, right 这两个字符是不做处理
void add(char left, char right)
{
	string t;
	// 遍历中间的字符
	for (char ch = left + 1; ch < right; ch++)
	{
		char tmp = ch;
		// 处理 p1
		if (p1 == 2 && islet(tmp)) tmp -= 32; // ⼩写变⼤写
		else if (p1 == 3) tmp = '*'; // 变成星号
		// 处理 p2
		for (int i = 0; i < p2; i++)
		{
			t += tmp;
		}
	}
	// 处理 p3
	if (p3 == 2) reverse(t.begin(), t.end());
	ret += t;
}
int main()
{
	cin >> p1 >> p2 >> p3 >> s;
	n = s.size();
	for (int i = 0; i < n; i++)
	{
		char ch = s[i];
		if (s[i] != '-' || i == 0 || i == n - 1) ret += ch;
		else
		{
			char left = s[i - 1], right = s[i + 1];
			// 判断是否展开
			if (isdig(left) && isdig(right) && right > left ||
				islet(left) && islet(right) && right > left)
			{
				// 展开
				add(left, right);
			}
			else
			{
				ret += ch;
			}
		}
	}
	cout << ret << endl;
	return 0;
}

二、高精度

2.1 ⾼精度加法

牛客网链接

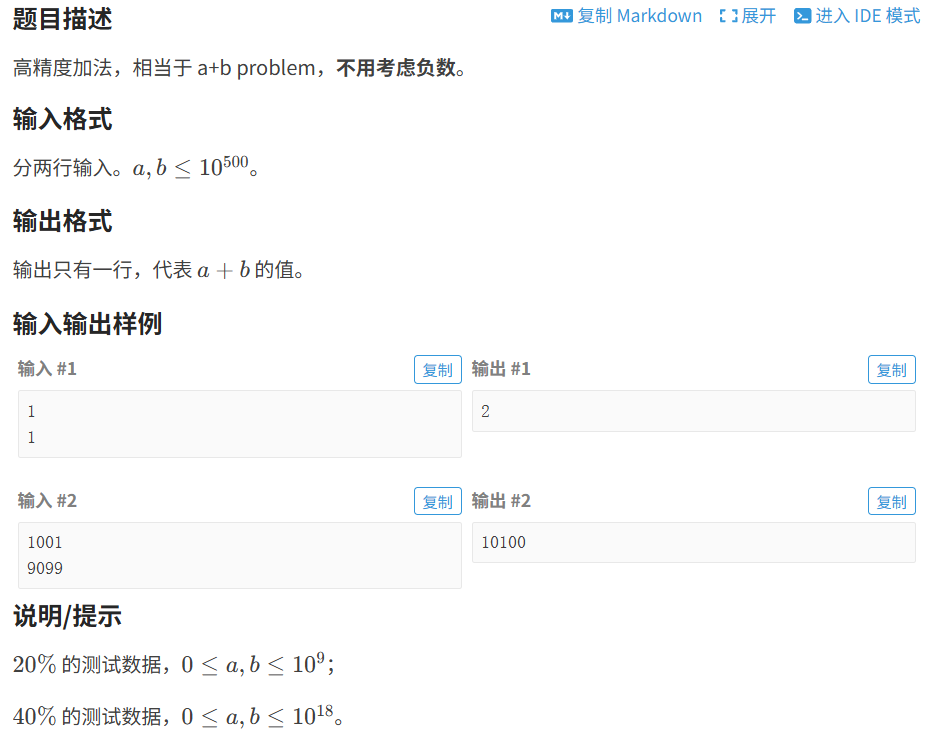
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N], b[N], c[N];
int la, lb, lc;
// ⾼精度加法的模版 - c = a + b;
void add(int c[], int a[], int b[])
{
	for (int i = 0; i < lc; i++)
	{
		c[i] += a[i] + b[i]; // 对应位相加，再加上进位
		c[i + 1] += c[i] / 10; // 处理进位
		c[i] %= 10; // 处理余数
	}
	if (c[lc]) lc++;
}
int main()
{
	string x, y; cin >> x >> y;
	// 1. 拆分每⼀位，逆序放在数组中
	la = x.size(); lb = y.size(); lc = max(la, lb);
	for (int i = 0; i < la; i++) a[la - 1 - i] = x[i] - '0';
	for (int i = 0; i < lb; i++) b[lb - 1 - i] = y[i] - '0';
	// 2. 模拟加法的过程
	add(c, a, b); // c = a + b
	// 输出结果
	for (int i = lc - 1; i >= 0; i--) cout << c[i];
	return 0;
}

2.2 ⾼精度减法

牛客网链接

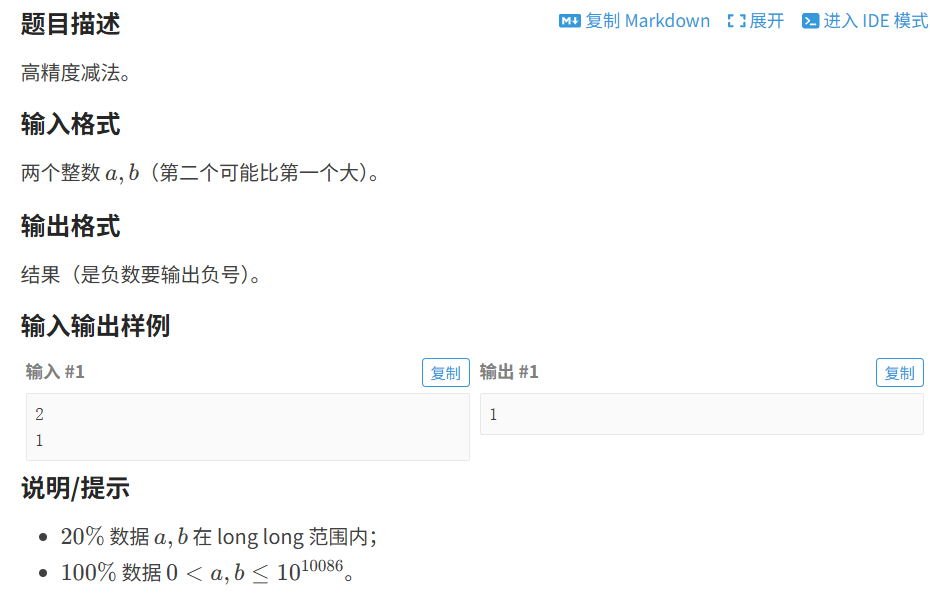
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N], b[N], c[N];
int la, lb, lc;
// ⽐⼤⼩
bool cmp(string& x, string& y)
{
	// 先⽐较⻓度
	if (x.size() != y.size()) return x.size() < y.size();
	// 再按照 字典序 的⽅式⽐较
	return x < y;
}
// ⾼精度减法的模板 - c = a - b
void sub(int c[], int a[], int b[])
{
	for (int i = 0; i < lc; i++)
	{
		c[i] += a[i] - b[i]; // 对应位相减，然后处理借位
		if (c[i] < 0)
		{
			c[i + 1] -= 1; // 借位
			c[i] += 10;
		}
	}
	// 处理前导零
	while (lc > 1 && c[lc - 1] == 0) lc--;
}
int main()
{
	string x, y; cin >> x >> y;
	// ⽐⼤⼩
	if (cmp(x, y))
	{
		swap(x, y);
		cout << '-';
	}
	// 1. 拆分每⼀位，然后逆序放在数组中
	la = x.size(); lb = y.size(); lc = max(la, lb);
	for (int i = 0; i < la; i++) a[la - i - 1] = x[i] - '0';
	for (int i = 0; i < lb; i++) b[lb - i - 1] = y[i] - '0';
	// 2. 模拟减法的过程
	sub(c, a, b); // c = a - b
	// 输出结果
	for (int i = lc - 1; i >= 0; i--) cout << c[i];
	return 0;
}

2.3 ⾼精度乘法

牛客网链接

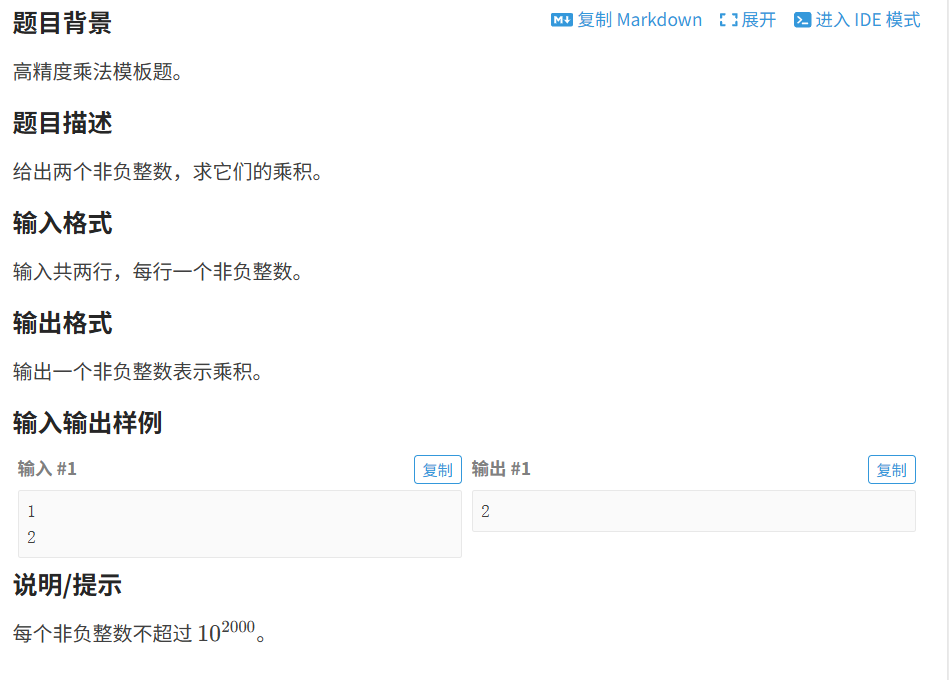
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N], b[N], c[N];
int la, lb, lc;
// ⾼精度乘法的模版 - c = a * b
void mul(int c[], int a[], int b[])
{
	// ⽆进位相乘,然后相加
	for (int i = 0; i < la; i++)
	{
		for (int j = 0; j < lb; j++)
		{
			c[i + j] += a[i] * b[j];
		}
	}
	// 处理进位
	for (int i = 0; i < lc; i++)
	{
		c[i + 1] += c[i] / 10;
		c[i] %= 10;
	}
	// 处理前导零
	while (lc > 1 && c[lc - 1] == 0) lc--;
}
int main()
{
	string x, y; cin >> x >> y;
	// 1. 拆分每⼀位，逆序放在数组中
	la = x.size(); lb = y.size(); lc = la + lb;
	for (int i = 0; i < la; i++) a[la - 1 - i] = x[i] - '0';
	for (int i = 0; i < lb; i++) b[lb - 1 - i] = y[i] - '0';
	// 2. 模拟乘法的过程
	mul(c, a, b); // c = a * b
	// 输出结果
	for (int i = lc - 1; i >= 0; i--) cout << c[i];
	return 0;
}

2.4 ⾼精度除法

牛客网链接

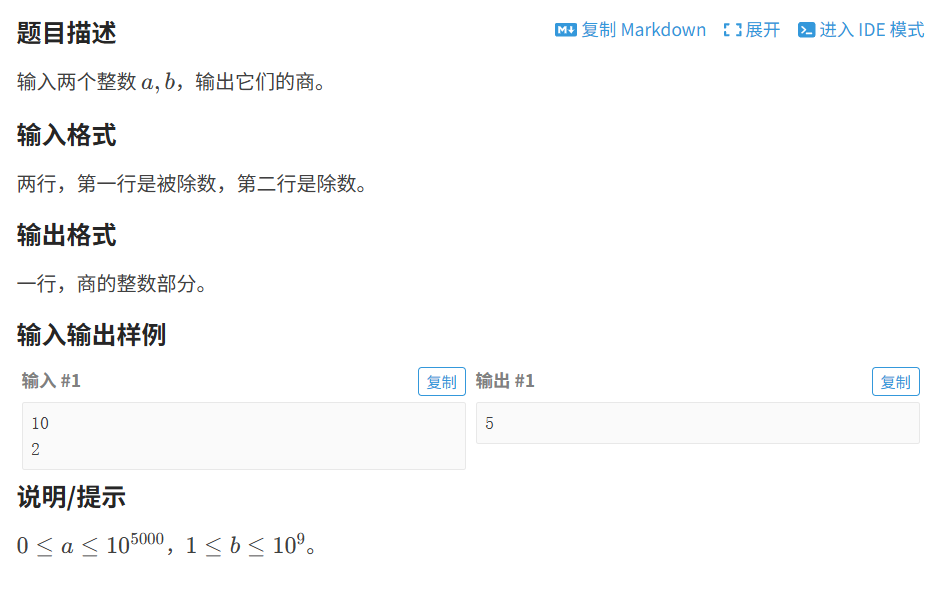
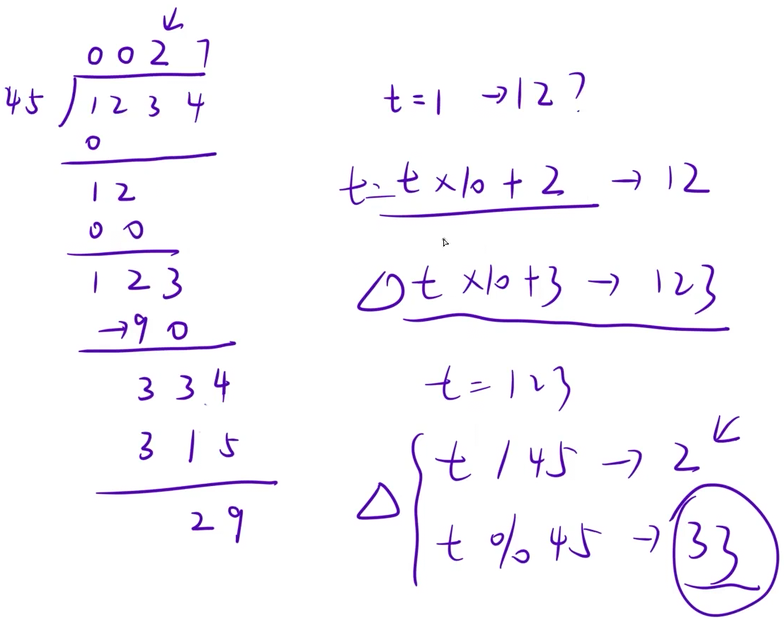
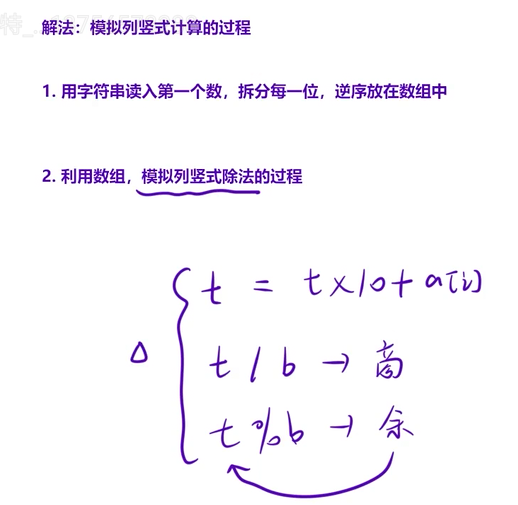
代码如下（示例）：

c 复制代码 
#include<iostream>
using namespace std;
const int N = 1e6 + 10;
typedef long long LL;
int a[N], b, c[N];
int la, lc;
// ⾼精度除法的模板 - c = a / b （⾼精度 / 低精度）
void sub(int c[], int a[], int b)
{
	LL t = 0; // 标记每次除完之后的余数
	for (int i = la - 1; i >= 0; i--)
	{
		// 计算当前的被除数
		t = t * 10 + a[i];
		c[i] = t / b;
		t %= b;
	}
	// 处理前导 0
	while (lc > 1 && c[lc - 1] == 0) lc--;
}
int main()
{
	string x; cin >> x >> b;
	la = x.size();
	for (int i = 0; i < la; i++) a[la - 1 - i] = x[i] - '0';
	// 模拟除法的过程
	lc = la;
	sub(c, a, b); // c = a / b
	for (int i = lc - 1; i >= 0; i--) cout << c[i];
	return 0;
}

三、枚举

3.1 普通枚举

3.1.1 铺地毯

牛客网链接




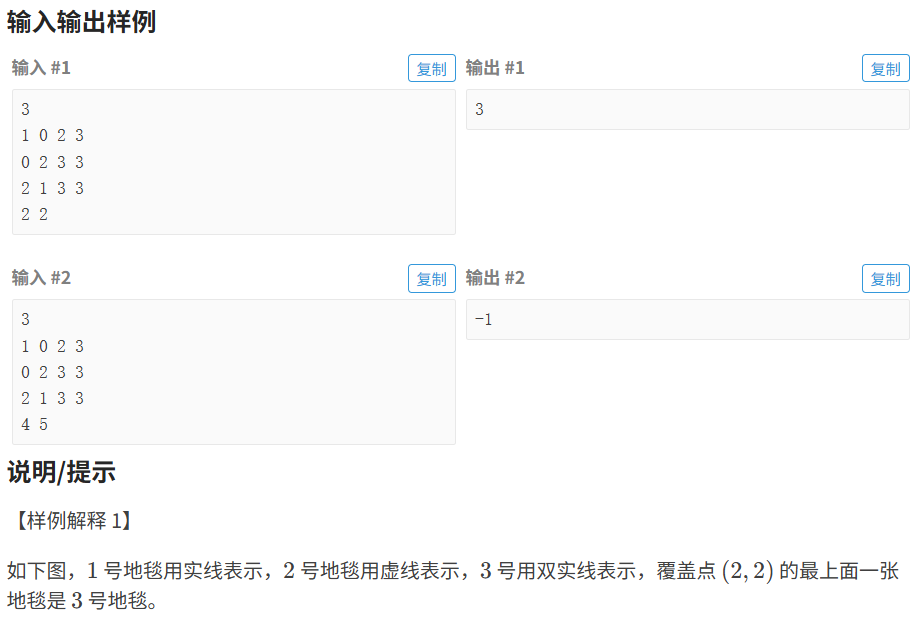
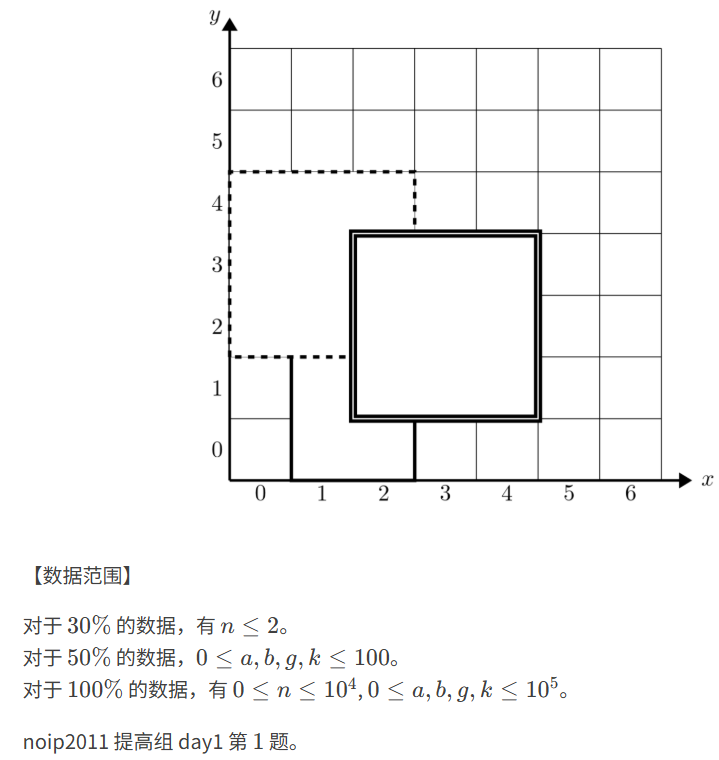
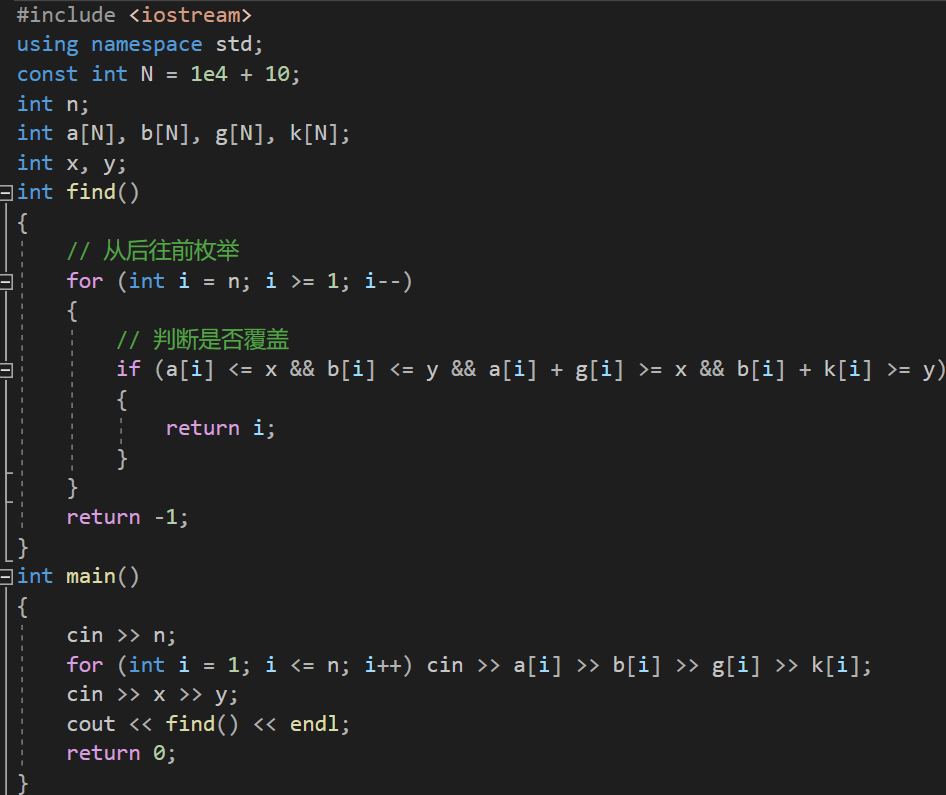
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
const int N = 1e4 + 10;
int n;
int a[N], b[N], g[N], k[N];
int x, y;
int find()
{
	// 从后往前枚举
	for (int i = n; i >= 1; i--)
	{
		// 判断是否覆盖
		if (a[i] <= x && b[i] <= y && a[i] + g[i] >= x && b[i] + k[i] >= y)
		{
			return i;
		}
	}
	return -1;
}
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i] >> b[i] >> g[i] >> k[i];
	cin >> x >> y;
	cout << find() << endl;
	return 0;
}

3.1.2 回⽂⽇期

牛客网链接




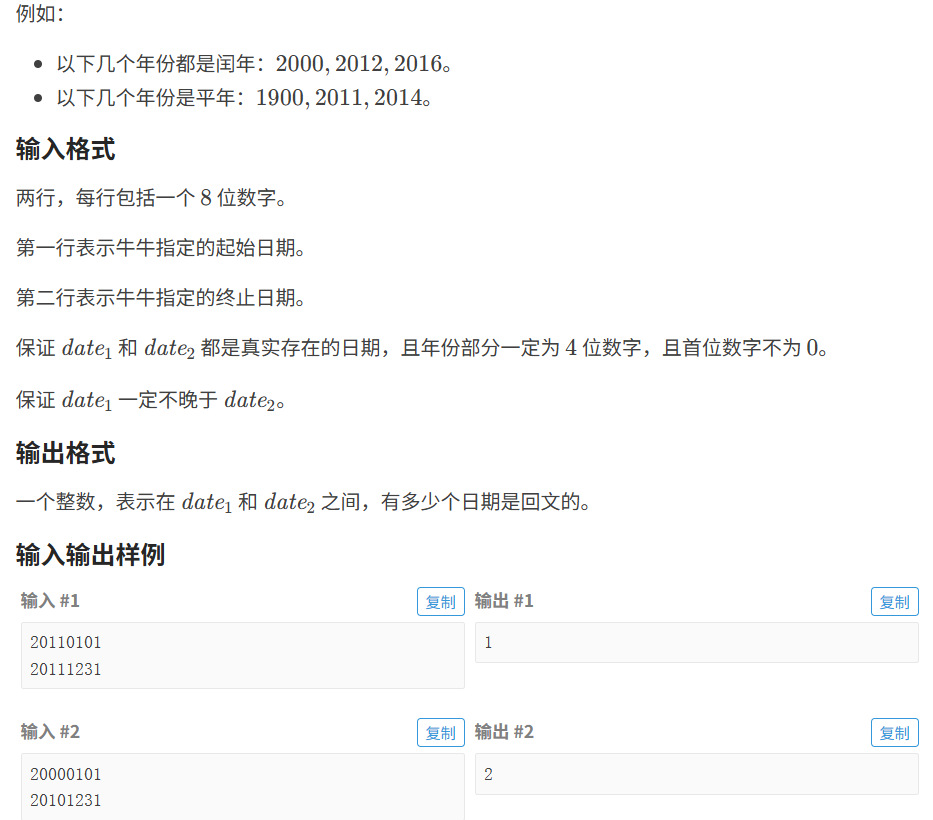
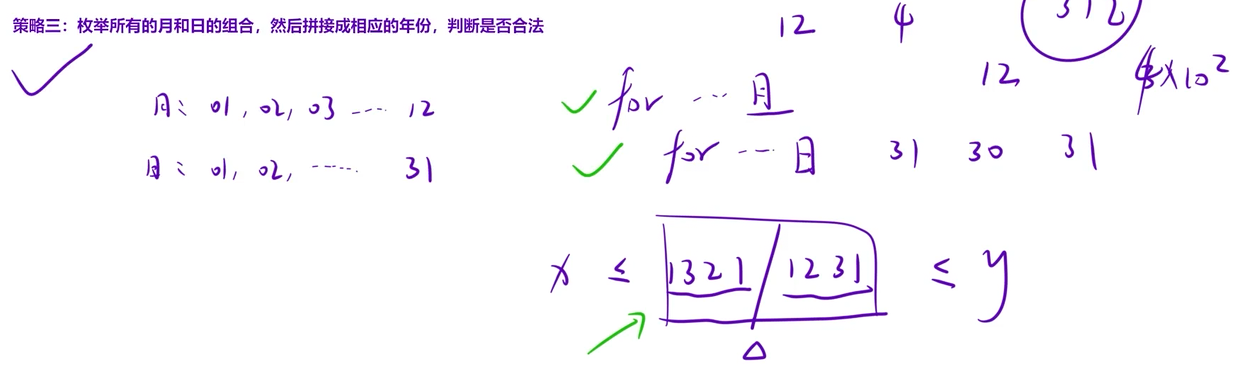
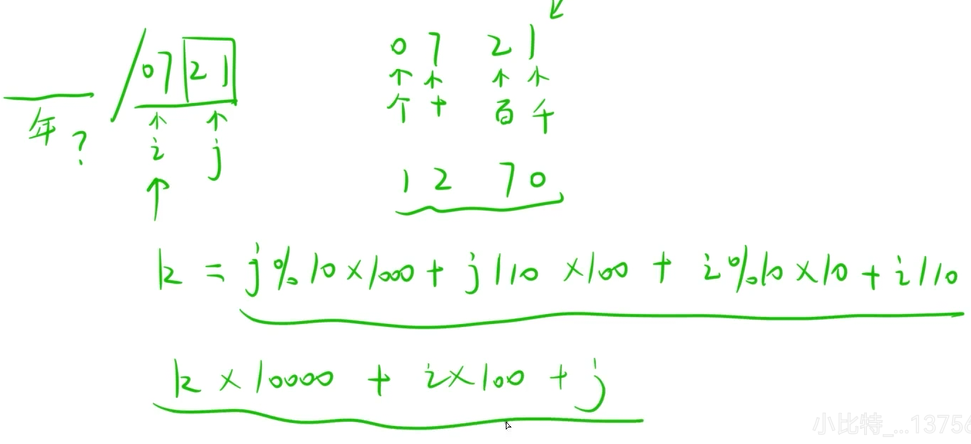
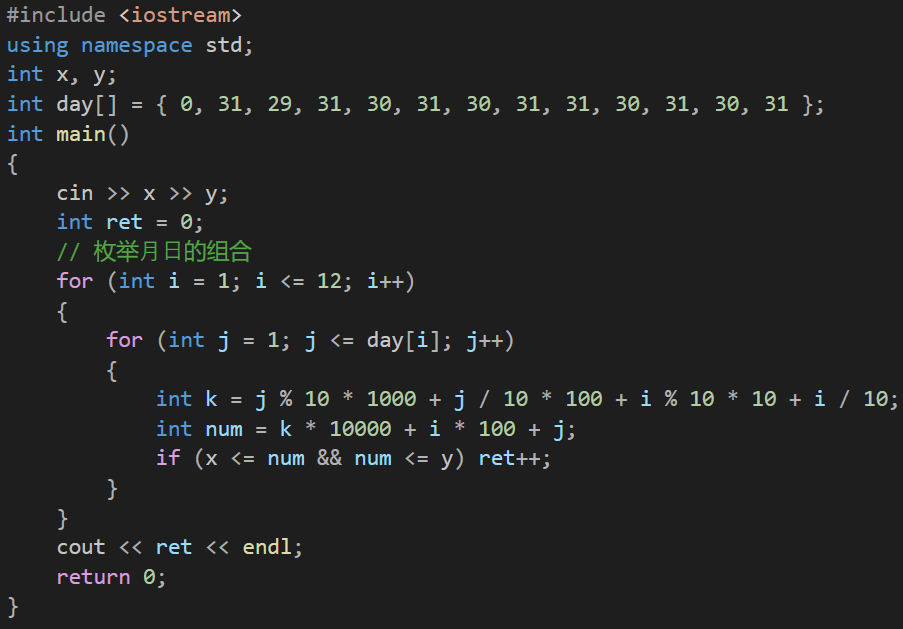
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
int x, y;
int day[] = { 0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31 };
int main()
{
	cin >> x >> y;
	int ret = 0;
	// 枚举⽉⽇的组合
	for (int i = 1; i <= 12; i++)
	{
		for (int j = 1; j <= day[i]; j++)
		{
			int k = j % 10 * 1000 + j / 10 * 100 + i % 10 * 10 + i / 10;
			int num = k * 10000 + i * 100 + j;
			if (x <= num && num <= y) ret++;
		}
	}
	cout << ret << endl;
	return 0;
}

3.1.3 扫雷

牛客网链接


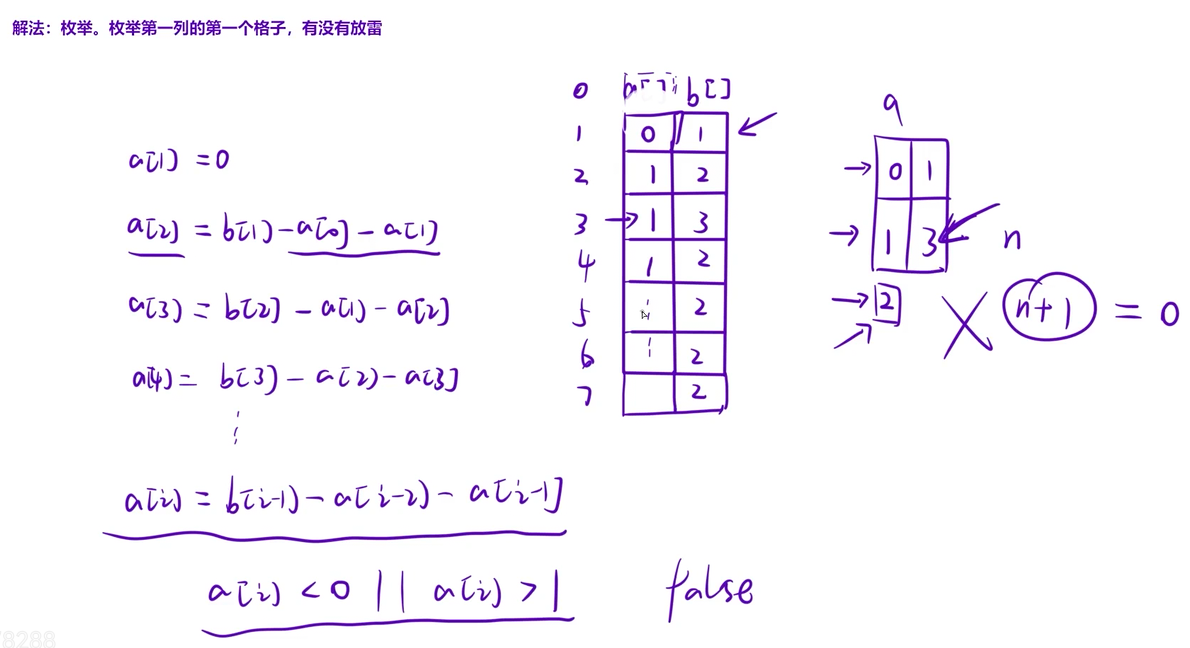
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
const int N = 1e4 + 10;
int n;
int a[N], b[N];
// 不放地雷
int check1()
{
	a[1] = 0;
	for (int i = 2; i <= n + 1; i++)
	{
		a[i] = b[i - 1] - a[i - 1] - a[i - 2];
		if (a[i] < 0 || a[i] > 1) return 0;
	}
	if (a[n + 1] == 0) return 1;
	else return 0;
}
int check2()
{
	a[1] = 1;
	for (int i = 2; i <= n + 1; i++)
	{
		a[i] = b[i - 1] - a[i - 1] - a[i - 2];
		if (a[i] < 0 || a[i] > 1) return 0;
	}
	if (a[n + 1] == 0) return 1;
	else return 0;
}
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> b[i];
	int ret = 0;
	ret += check1(); // a[1] 不放地雷
	ret += check2(); // a[1] 放地雷
	cout << ret << endl;
	return 0;
}

3.2 ⼆进制枚举

3.2.1 ⼦集

牛客网链接

代码如下（示例）：

c 复制代码 
class Solution
{
public:
	vector<vector<int>> subsets(vector<int>& nums)
	{
		vector<vector<int>> ret;
		int n = nums.size();
		// 枚举所有的状态
		for (int st = 0; st < (1 << n); st++)
		{
			// 根据 st 的状态，还原出要选的数
			vector<int> tmp; // 从当前选的⼦集
			for (int i = 0; i < n; i++)
			{
				if ((st >> i) & 1) tmp.push_back(nums[i]);
			}
			ret.push_back(tmp);
		}
		return ret;
	}
};

3.2.2 费解的开关

牛客网链接




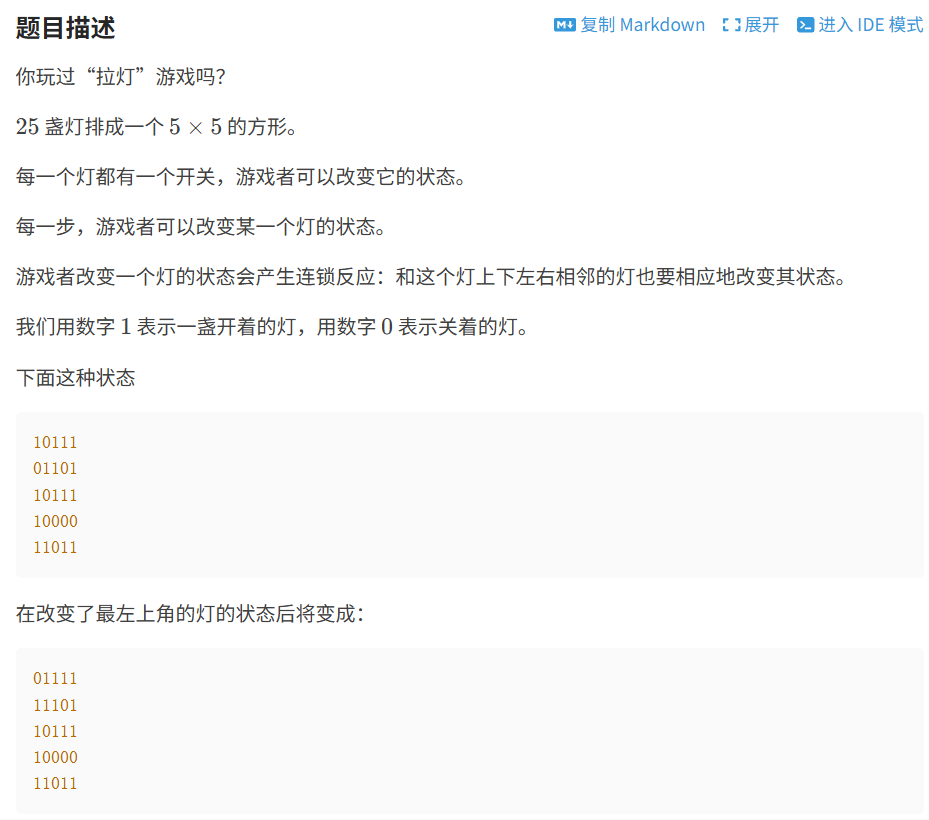
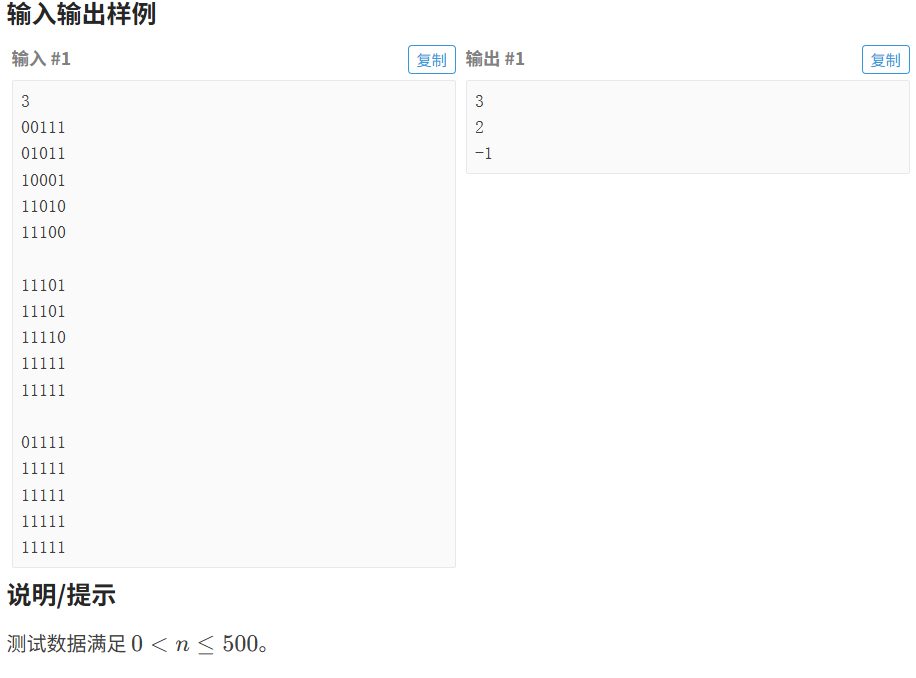
代码如下（示例）：

c 复制代码 
#include <iostream>
#include <cstring>
using namespace std;
const int N = 10;
int n = 5;
int a[N]; // ⽤⼆进制表⽰，来存储灯的状态
int t[N]; // 备份 a 数组
// 计算 x 的⼆进制表⽰中⼀共有多少个 1
int calc(int x)
{
	int cnt = 0;
	while (x)
	{
		cnt++;
		x &= x - 1;
	}
	return cnt;
}
int main()
{
	int T; cin >> T;
	while (T--)
	{
		// 多组测试时，⼀定要注意清空之前的数据
		memset(a, 0, sizeof a);
		for (int i = 0; i < n; i++)
		{
			for (int j = 0; j < n; j++)
			{
				char ch; cin >> ch;
				// 存成相反的
				if (ch == '0') a[i] |= 1 << j;
			}
		}
		int ret = 0x3f3f3f3f; // 统计所有合法的按法中的最⼩值
		// 枚举第⼀⾏所有的按法
		for (int st = 0; st < (1 << n); st++)
		{
			memcpy(t, a, sizeof a);
			int push = st; // 当前⾏的按法
			int cnt = 0; // 统计当前按法下⼀共按了多少次
			// 依次计算后续⾏的结果以及按法
			for (int i = 0; i < n; i++)
			{
				cnt += calc(push);
				// 修改当前⾏被按的结果
				t[i] = t[i] ^ push ^ (push << 1) ^ (push >> 1);
				t[i] &= (1 << n) - 1; // 清空影响
				// 修改下⼀⾏的状态
				t[i + 1] ^= push;
				// 下⼀⾏的按法
				push = t[i];
			}
			if (t[n - 1] == 0) ret = min(ret, cnt);
		}
		if (ret > 6) cout << -1 << endl;
		else cout << ret << endl;
	}
	return 0;
}

3.2.3 Even Parity

牛客网链接


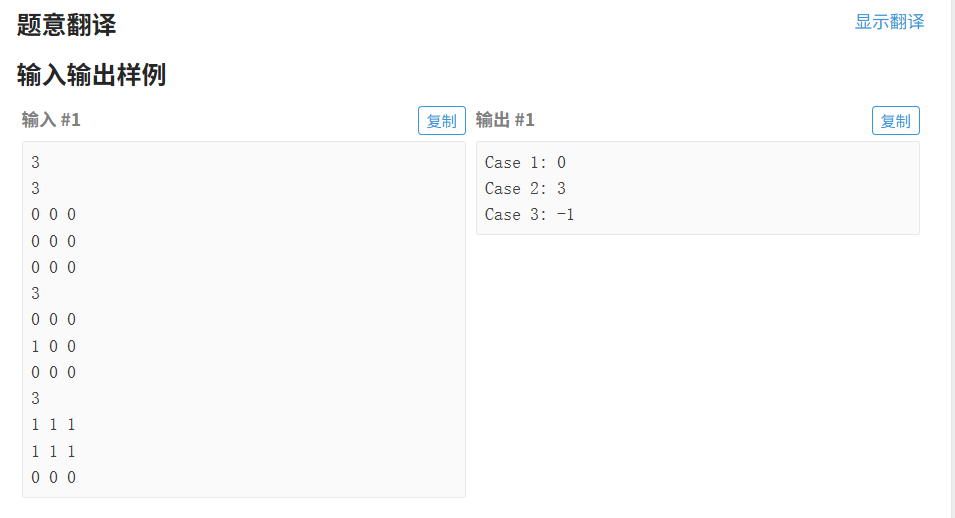
代码如下（示例）：

c 复制代码 
#include <iostream>
#include <cstring>
using namespace std;
const int N = 20;
int n;
int a[N]; // ⽤⼆进制存储状态
int t[N]; // 备份
// 判断 x->y 是否合法
// 返回 -1，表⽰不合法
// 其余的数，表⽰合法，并且表⽰ 0->1 的次数
int calc(int x, int y)
{
	int sum = 0;
	for (int i = 0; i < n; i++)
	{
		if (((x >> i) & 1) == 0 && ((y >> i) & 1) == 1) sum++;
		if (((x >> i) & 1) == 1 && ((y >> i) & 1) == 0) return -1;
	}
	return sum;
}
int solve()
{
	int ret = 0x3f3f3f3f; // 记录最⼩的改变次数
	// 枚举第⼀⾏的最终状态
	for (int st = 0; st < (1 << n); st++)
	{
		memcpy(t, a, sizeof a);
		int change = st;
		int cnt = 0; // 统计 0->1 的次数
		bool flag = 1;
		for (int i = 1; i <= n; i++)
		{
			// 先判断 change 是否合法
			int c = calc(t[i], change);
			if (c == -1)
			{
				flag = 0;
				break;
			}
			cnt += c; // 累加次数
			// 当前⾏的最终状态
			t[i] = change;
			// 计算下⼀⾏的最终状态
			change = t[i - 1] ^ (t[i] << 1) ^ (t[i] >> 1);
			change &= (1 << n) - 1;
		}
		if (flag) ret = min(ret, cnt);
	}
	if (ret == 0x3f3f3f3f) return -1;
	else return ret;
}
int main()
{
	int T; cin >> T;
	for (int k = 1; k <= T; k++)
	{
		// 多组测试数据，记得清空
		memset(a, 0, sizeof a);
		cin >> n;
		for (int i = 1; i <= n; i++) // 避免越界访问
		{
			for (int j = 0; j < n; j++)
			{
				int x; cin >> x;
				if (x) a[i] |= 1 << j;
			}
		}
		printf("Case %d: %d\n", k, solve());
	}
	return 0;
}

四、前缀和

4.1 ⼀维前缀和

牛客网链接

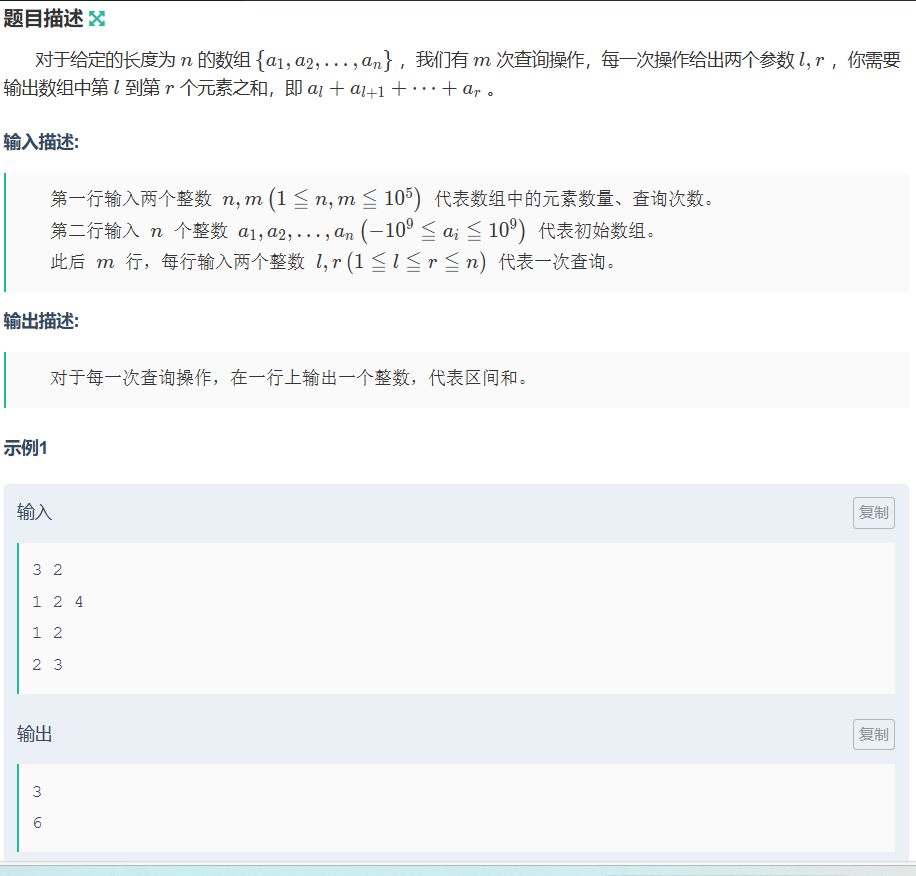
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int n, q;
LL a[N];
LL f[N]; // 前缀和数组
int main()
{
	cin >> n >> q;
	for (int i = 1; i <= n; i++) cin >> a[i];
	// 处理前缀和数组
	for (int i = 1; i <= n; i++)
	{
		f[i] = f[i - 1] + a[i];
	}
	// 处理 q 次询问
	while (q--)
	{
		int l, r; cin >> l >> r;
		cout << f[r] - f[l - 1] << endl;
	}
	return 0;
}

4.2 最⼤⼦段和

牛客网链接

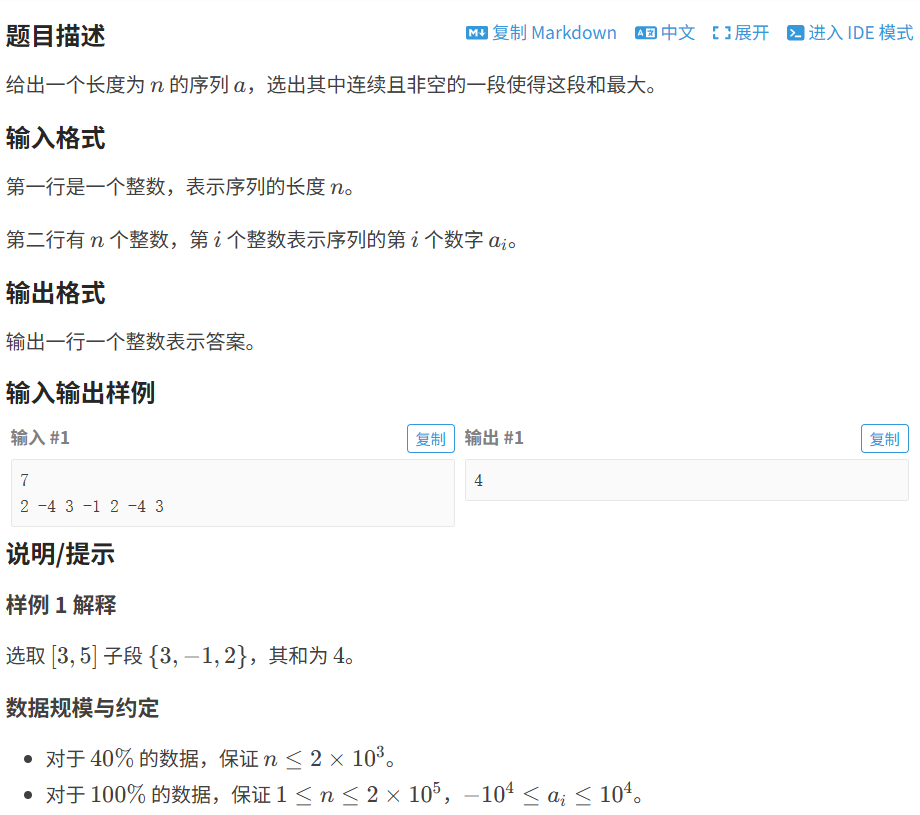
代码如下（示例）：

c 复制代码 
#include<iostream>
using namespace std;
int n, x;
const int N = 2e5 + 10;
int f[N];

int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> x;
		f[i] = f[i - 1] + x;
	}
	int ret = -0x3f3f3f3f;
	int prevmin = 0;
	for (int i = 1; i <= n; i++)
	{
		ret = max(ret, f[i] - prevmin);
		prevmin = min(prevmin, f[i]);
	}
	cout << ret << endl;
 }

4.3 ⼆维前缀和

牛客网链接



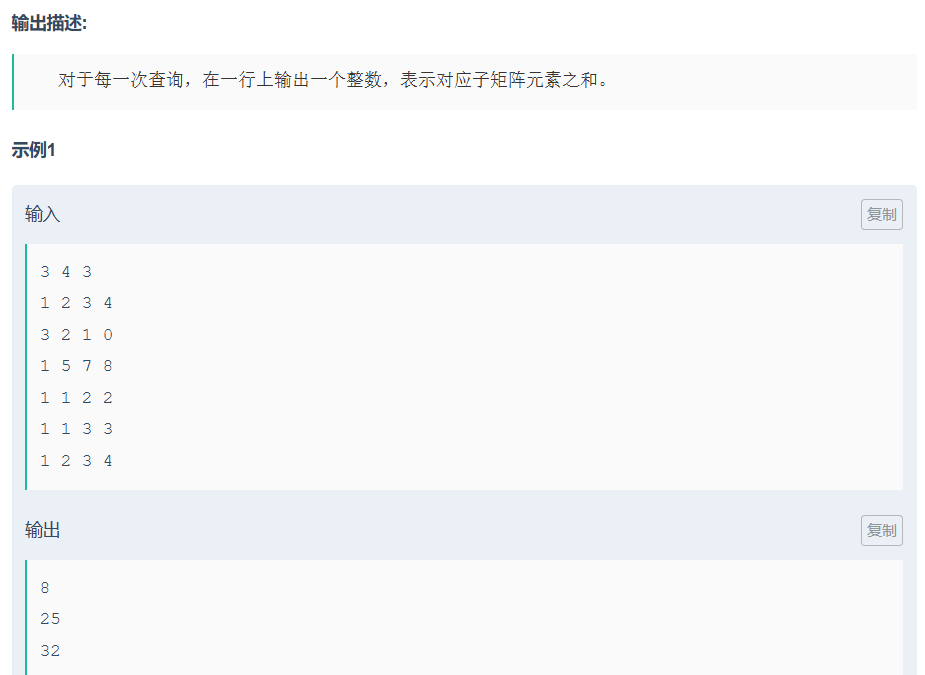
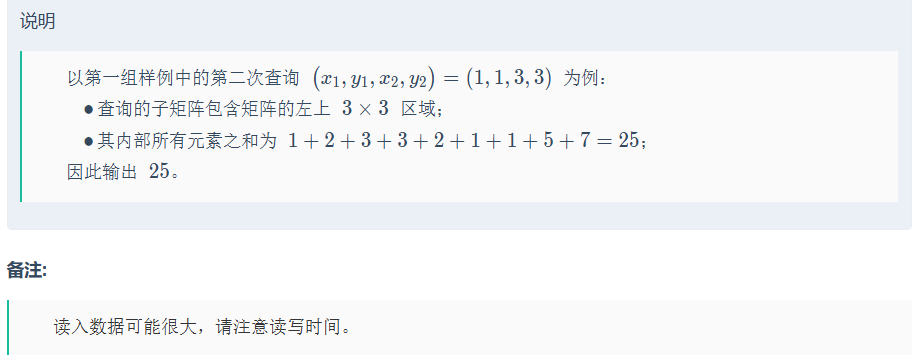
两个公式即可！

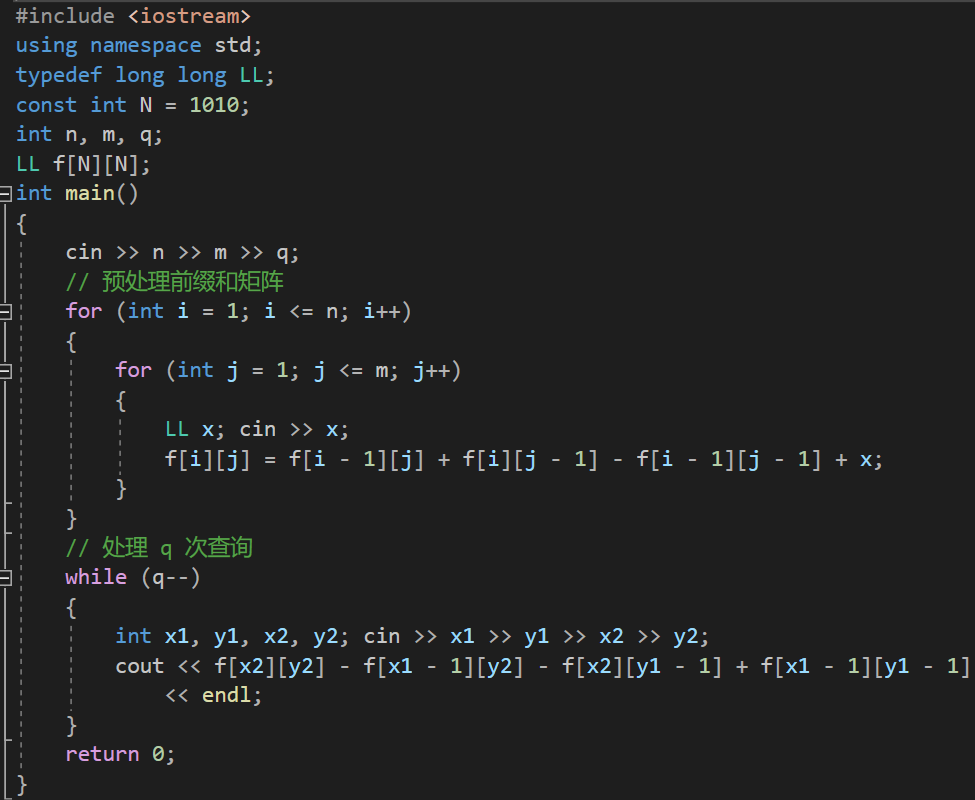
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1010;
int n, m, q;
LL f[N][N];
int main()
{
	cin >> n >> m >> q;
	// 预处理前缀和矩阵
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			LL x; cin >> x;
			f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + x;
		}
	}
	// 处理 q 次查询
	while (q--)
	{
		int x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2;
		cout << f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1]
			<< endl;
	}
	return 0;
}

4.4 激光炸弹

牛客网链接

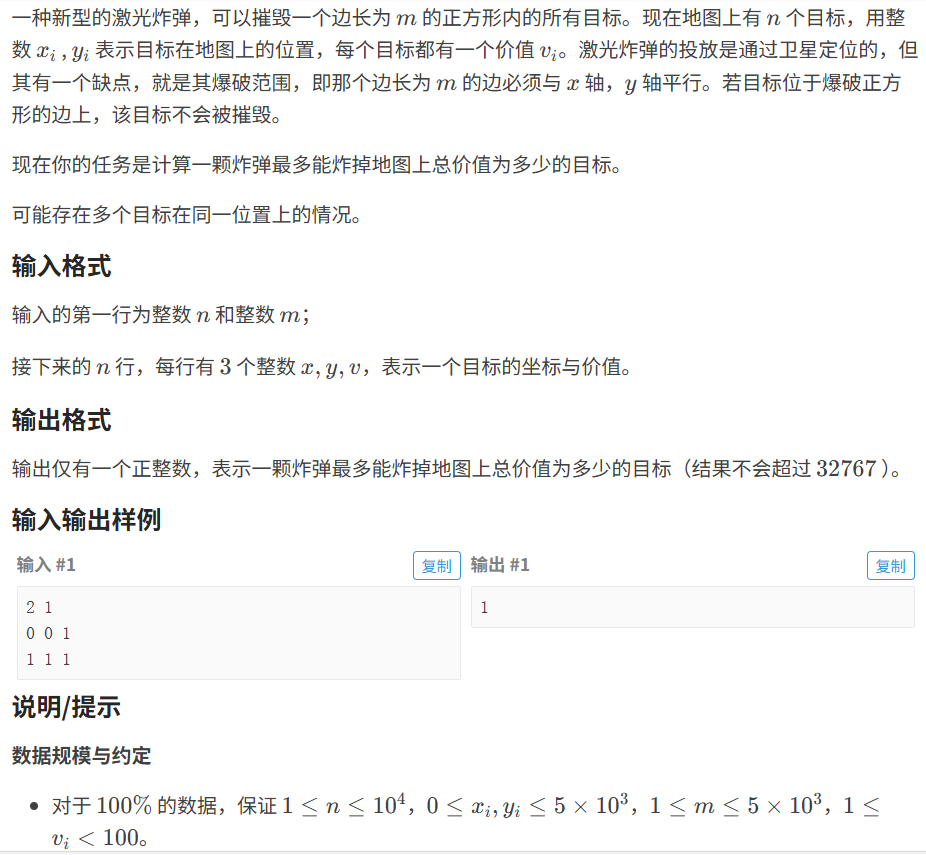
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
const int N = 5010;
int n, m;
int a[N][N];
int f[N][N]; // 前缀和矩阵
int main()
{
	cin >> n >> m;
	while (n--)
	{
		int x, y, v; cin >> x >> y >> v;
		x++, y++; // 下标从 1 开始计数
		a[x][y] += v; // 同⼀个位置有可能有多个⽬标
	}
	n = 5001;
	// 预处理前缀和矩阵
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + a[i][j];
		}
	}
	int ret = 0;
	m = min(m, n); // 如果 m 很⼤，相当于就是把整个区域全部摧毁
	// 枚举所有边⻓为 m 的正⽅形
	for (int x2 = m; x2 <= n; x2++)
	{
		for (int y2 = m; y2 <= n; y2++)
		{
			int x1 = x2 - m + 1, y1 = y2 - m + 1;
			ret = max(ret, f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 -
				1][y1 - 1]);
		}
	}
	cout << ret << endl;
	return 0;
}

五、差分

5.1 ⼀维差分

牛客网链接






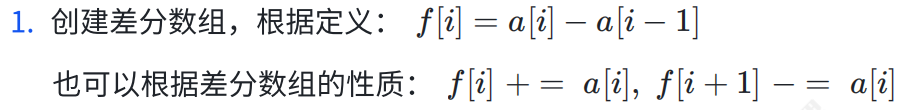
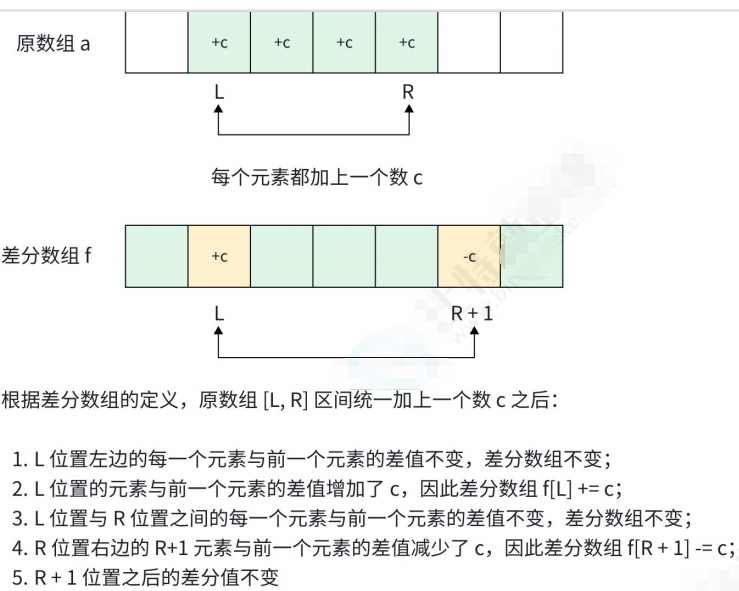
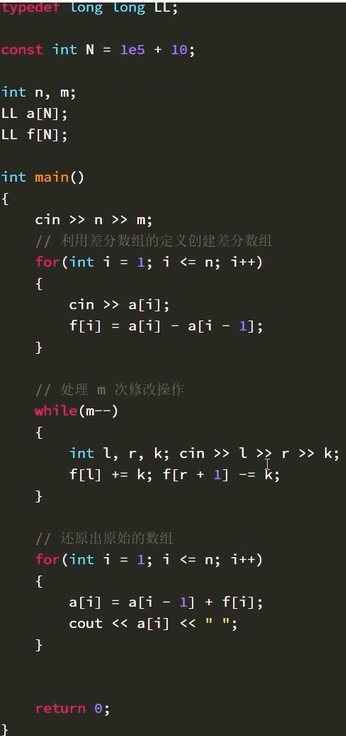
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int n, m;
LL f[N]; // 差分数组
int main()
{
	cin >> n >> m;
	// 利⽤差分数组的性质，创建差分数组
	for (int i = 1; i <= n; i++)
	{
		LL x; cin >> x;
		f[i] += x;
		f[i + 1] -= x;
	}
	// 处理 m 次修改操作
	while (m--)
	{
		LL l, r, k; cin >> l >> r >> k;
		f[l] += k; f[r + 1] -= k;
	}
	// 还原出原始的数组
	for (int i = 1; i <= n; i++)
	{
		f[i] = f[i - 1] + f[i];
		cout << f[i] << " ";
	}
	return 0;
}

5.2 海底⾼铁

牛客网链接


代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int n, m;
LL f[N]; // 差分数组
int main()
{
	cin >> n >> m;
	// x->y
	int x; cin >> x;
	for (int i = 2; i <= m; i++)
	{
		int y; cin >> y;
		// x -> y
		if (x > y)
		{
			f[y]++;
			f[x]--;
		}
		else
		{
			f[x]++;
			f[y]--;
		}
		x = y;
	}
	// 利⽤差分数组，还原出原数组
	for (int i = 1; i <= n; i++) f[i] += f[i - 1];
	// 直接求结果
	LL ret = 0;
	for (int i = 1; i < n; i++)
	{
		LL a, b, c; cin >> a >> b >> c;
		ret += min(a * f[i], c + b * f[i]);
	}
	cout << ret << endl;
	return 0;
}

5.3 ⼆维差分

牛客网链接




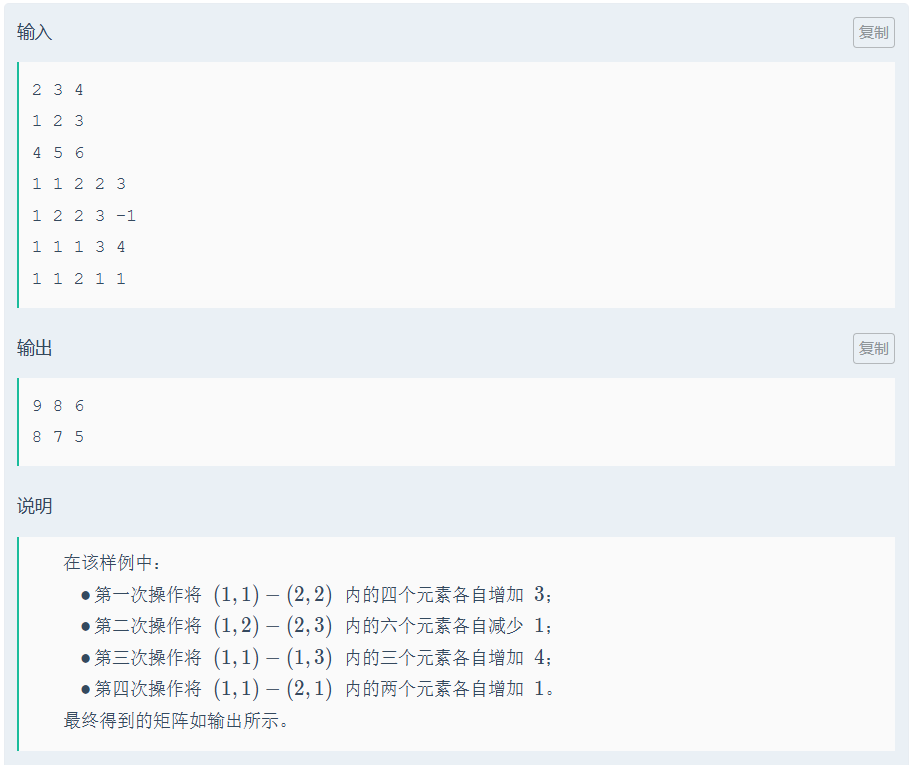
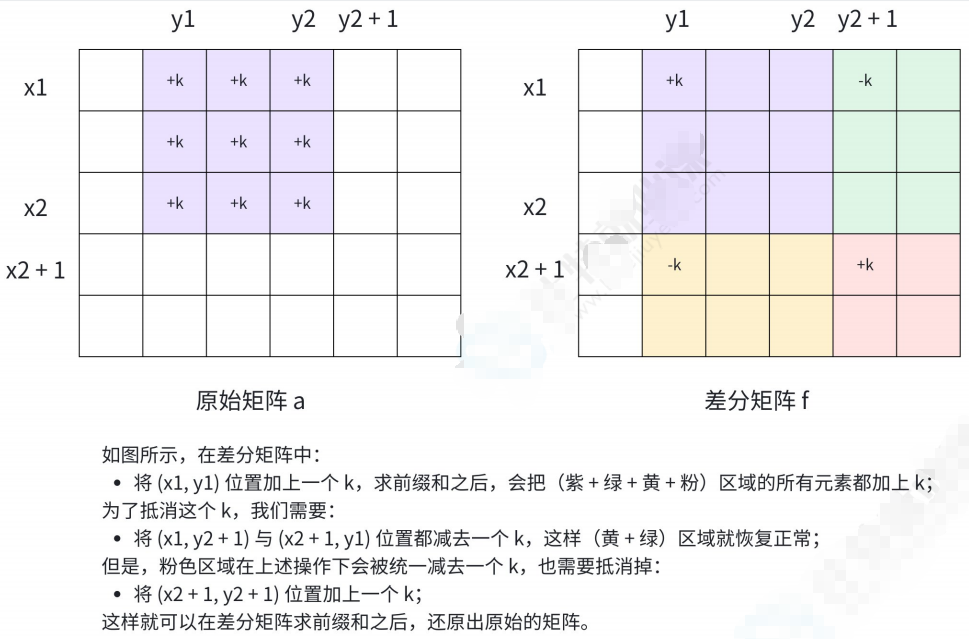
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1010;
int n, m, q;
LL f[N][N]; // 差分矩阵
// 差分矩阵的性质
void insert(int x1, int y1, int x2, int y2, LL k)
{
	f[x1][y1] += k; f[x1][y2 + 1] -= k; f[x2 + 1][y1] -= k; f[x2 + 1][y2 + 1]
		+= k;
}
int main()
{
	cin >> n >> m >> q;
	// 预处理差分矩阵
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			LL x; cin >> x;
			// [i, j]为左上⻆，[i, j]为右下⻆的矩阵，统⼀加上 x
			insert(i, j, i, j, x);
		}
	}
	// 处理 q 次修改操作
	while (q--)
	{
		LL x1, y1, x2, y2, k; cin >> x1 >> y1 >> x2 >> y2 >> k;
		insert(x1, y1, x2, y2, k);
	}
	// 利⽤前缀和还原出修改之后的数组
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + f[i][j];
			cout << f[i][j] << " ";
		}
		cout << endl;
	}
	return 0;
}

5.4 地毯

牛客网链接



代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int f[N][N]; // 差分矩阵
// 差分数组的性质
void insert(int x1, int y1, int x2, int y2, int k)
{
	f[x1][y1] += k; f[x1][y2 + 1] -= k; f[x2 + 1][y1] -= k; f[x2 + 1][y2 + 1]
		+= k;
}
int main()
{
	cin >> n >> m;
	// 构建差分数组
	while (m--)
	{
		int x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2;
		insert(x1, y1, x2, y2, 1);
	}
	// 利⽤前缀和还原修改之后的数组
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + f[i][j];
			cout << f[i][j] << " ";
		}
		cout << endl;
	}
	return 0;
}

六、双指针

6.1 唯⼀的雪花

牛客网链接


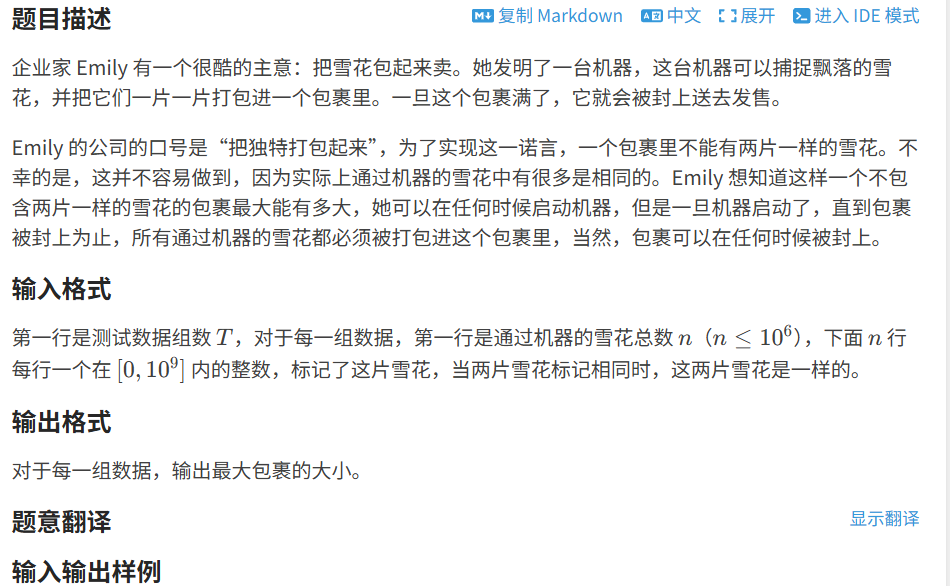
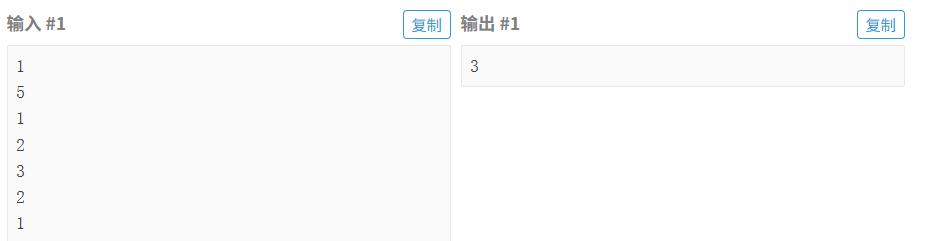
滑动窗口 + 哈希表！

代码如下（示例）：

c 复制代码 
#include <iostream>
#include <unordered_map>
using namespace std;
const int N = 1e6 + 10;
int n;
int a[N];
int main()
{
	int T; cin >> T;
	while (T--)
	{
		cin >> n;
		for (int i = 1; i <= n; i++) cin >> a[i];
		// 初始化
		int left = 1, right = 1, ret = 0;
		unordered_map<int, int> mp; // 维护窗⼝内所有元素出现的次数
		while (right <= n)
		{
			// 进窗⼝
			mp[a[right]]++;
			// 判断
			while (mp[a[right]] > 1)
			{
				// 出窗⼝
				mp[a[left]]--;
				left++;
			}
			// 窗⼝合法，更新结果
			ret = max(ret, right - left + 1);
			right++;
		}
		cout << ret << endl;
	}
	return 0;
}

6.2 逛画展

牛客网链接


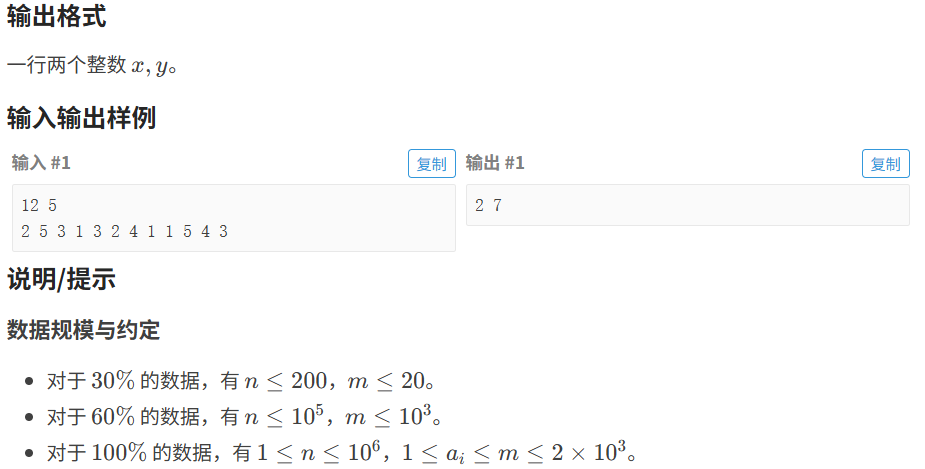
代码如下（示例）：

c 复制代码 
#include<iostream>
using namespace std;
const int N = 1e6 + 10, M = 2e3 + 10;
int n, m;
int a[N];
int kind; // 窗⼝内有效元素的个数
int mp[N]; // 统计窗⼝内每个元素出现的次数
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++) cin >> a[i];
	int left = 1, right = 1;
	int ret = n, begin = 1;
	while (right <= n)
	{
		// 进窗⼝
		if (mp[a[right]]++ == 0) kind++;
		// 判断
		while (kind == m)
		{
			// 更新结果
			int len = right - left + 1;
			if (len < ret)
			{
				ret = len;
				begin = left;
			}
			// 出窗⼝
			if (mp[a[left]]-- == 1) kind--;
			left++;
		}
		right++;
	}
	cout << begin << " " << begin + ret - 1 << endl;
	return 0;
}

6.3 字符串

牛客网链接

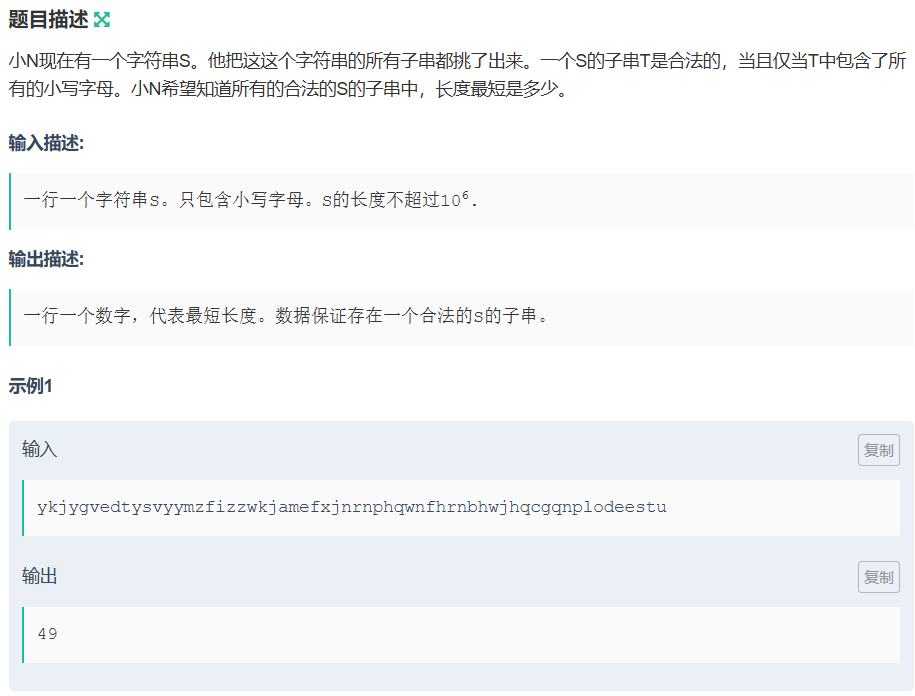
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
string s;
int mp[26]; // 统计每个⼩写字符出现的次数
int kind; // 窗⼝内⼩写字符的种类
int main()
{
	cin >> s;
	int n = s.size();
	int ret = n;
	// 初始化
	for (int left = 0, right = 0; right < n; right++)
	{
		// 进窗⼝
		if (mp[s[right] - 'a']++ == 0) kind++;
		// 判断
		while (kind == 26)
		{
			// 更新结果
			ret = min(ret, right - left + 1);
			// 出窗⼝
			if (mp[s[left] - 'a']-- == 1) kind--;
			left++;
		}
	}
	cout << ret << endl;
	return 0;
}

6.4 丢⼿绢

牛客网链接



代码如下（示例）：

c 复制代码 
#include<iostream>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int n;
LL a[N];
int main()
{
	cin >> n;
	LL sum = 0;
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i];
		sum += a[i];
	}
	int left = 1, right = 1;
	LL k = 0;
	LL ret = 0;
	while (right <= n)
	{
		k += a[right];
		while (2 * k >= sum)
		{
			// ⽤ sum - k 来更新结果
			ret = max(ret, sum - k);
			k -= a[left++];
		}
		// ⽤ k 来更新结果
		ret = max(ret, k);
		right++;
	}
	cout << ret << endl;
	return 0;
}

七、二分算法

模板题

牛客网链接

代码如下（示例）：

c 复制代码 
class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) 
    {
        if(nums.size() == 0) return {-1,-1};
        int left = 0 , right = nums.size() - 1;
        // 先判断左端点
        int begin = 0;
        while(left < right)
        {
            int mid = left + (right - left) / 2;
            if(nums[mid] < target) left = mid + 1;
            else right = mid;
        }
        if(nums[left] != target) return {-1 , -1};
        else begin = left;
        // 再判断右端点
        left = 0 , right = nums.size() - 1;
        while(left < right)
        {
            int mid = left + (right - left + 1) / 2;
            if(nums[mid]  <= target) left = mid;
            else right = mid -1;
        }
        return {begin , right};
    }
};

7.1 ⼆分查找

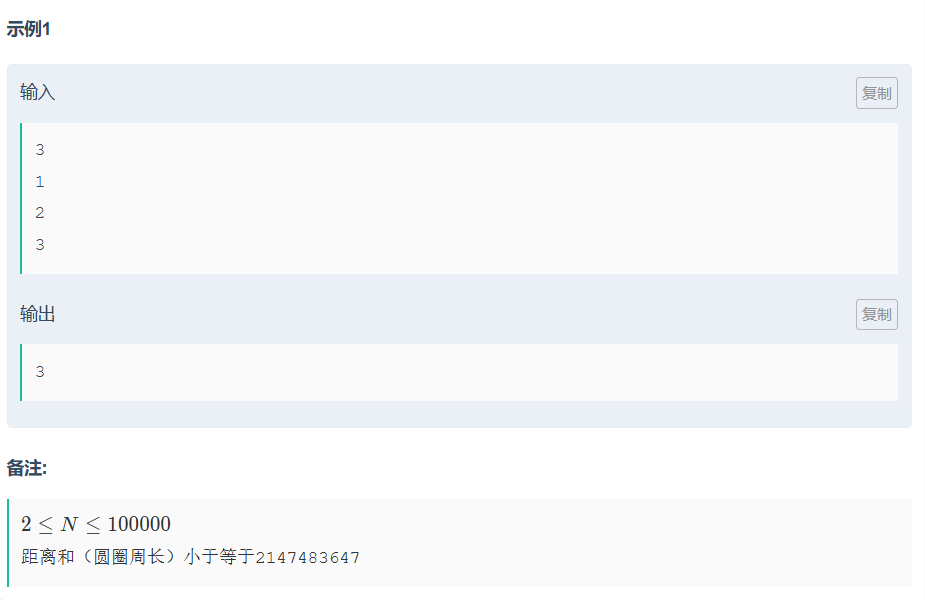
7.1.1 ⽜可乐和魔法封印

牛客网链接


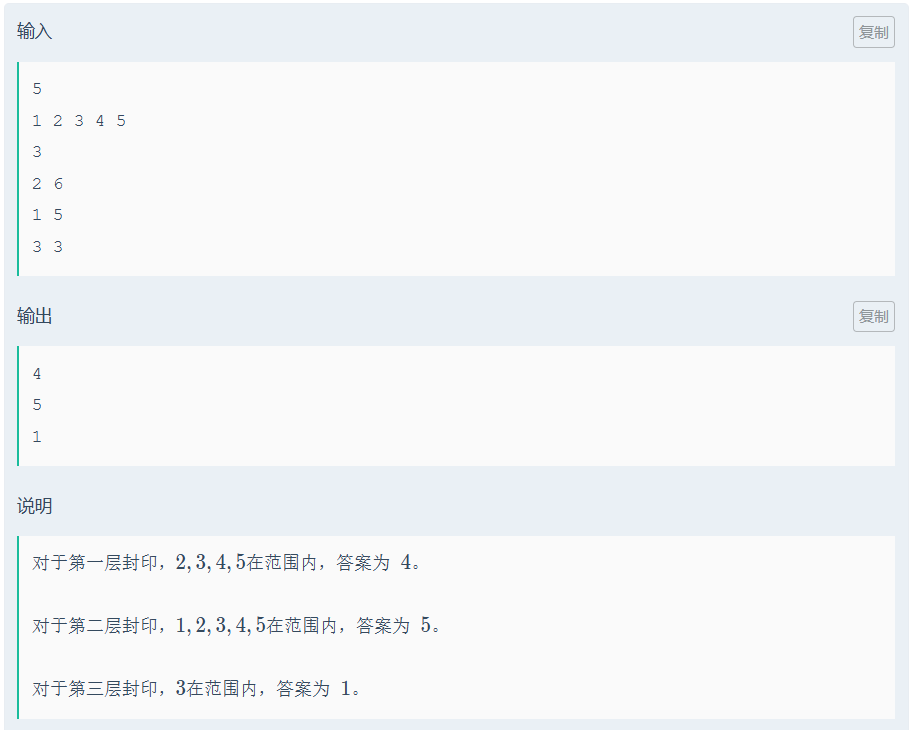
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int n;
int a[N];
int binary_search(int x, int y)
{
	// ⼤于等于 x 的最⼩元素
	int left = 1, right = n;
	while (left < right)
	{
		int mid = (left + right) / 2;
		if (a[mid] >= x) right = mid;
		else left = mid + 1;
	}
	if (a[left] < x) return 0;
	int tmp = left;
	// ⼩于等于 y 的最⼤元素
	left = 1, right = n;
	while (left < right)
	{
		int mid = (left + right + 1) / 2;
		if (a[mid] <= y) left = mid;
		else right = mid - 1;
	}
	if (a[left] > y) return 0;
	return left - tmp + 1;
}
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	int Q; cin >> Q;
	while (Q--)
	{
		int x, y; cin >> x >> y;
		cout << binary_search(x, y) << endl;
	}
	return 0;
}

7.1.2 A-B 数对

牛客网链接



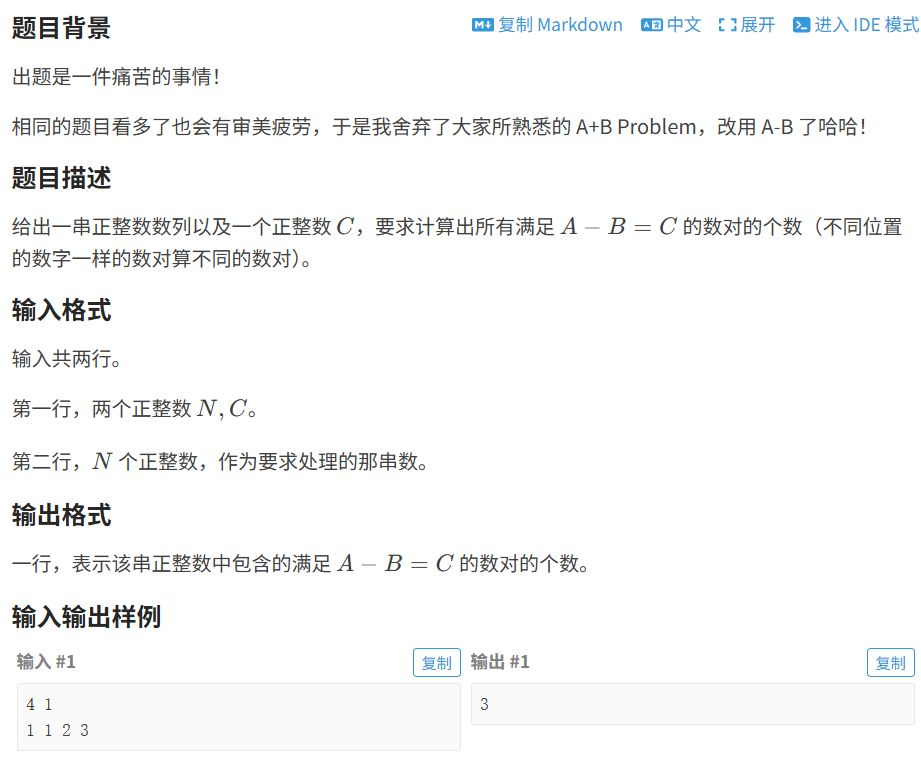
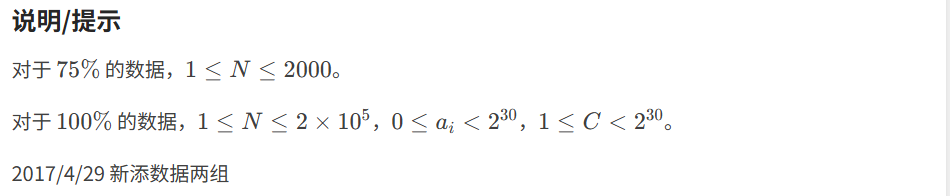
代码如下（示例）：

c 复制代码 
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 2e5 + 10;
LL n, c;
LL a[N];
int main()
{
cin >> n >> c;
for(int i = 1; i <= n; i++) cin >> a[i];
sort(a + 1, a + 1 + n);
LL ret = 0;
for(int i = 2; i <= n; i++)
{
// a[i]
LL b = a[i] - c;
ret += upper_bound(a + 1, a + i, b) - lower_bound(a + 1, a + i, b);
}
cout << ret << endl;
return 0;
}

7.1.3 烦恼的⾼考志愿

牛客网链接


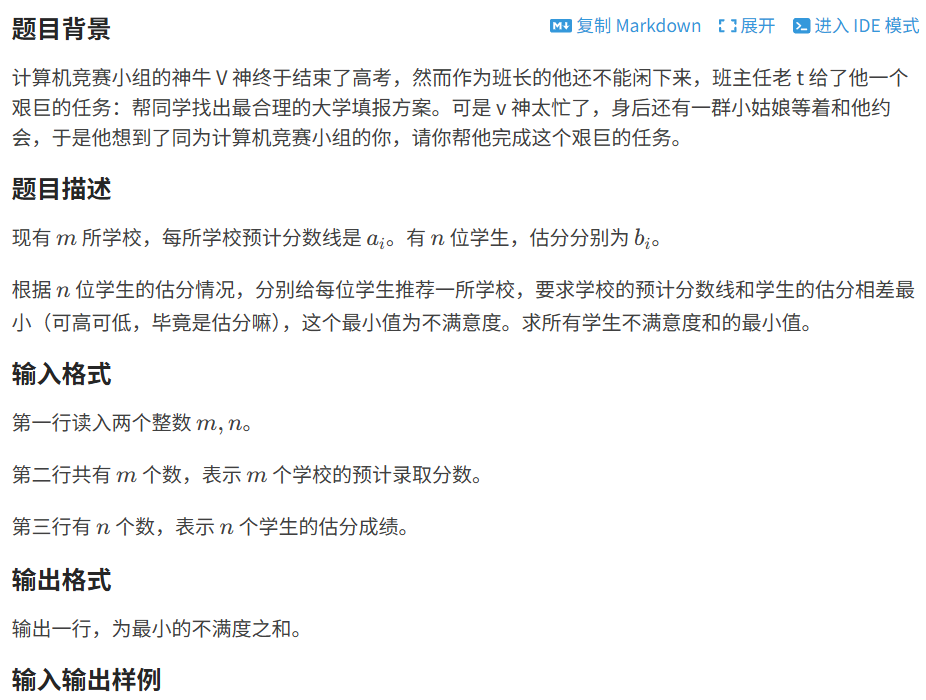
代码如下（示例）：

c 复制代码 
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int n, m;
LL a[N];
int find(LL x)
{
	int left = 1, right = m;
	while (left < right)
	{
		int mid = (left + right) / 2;
		if (a[mid] >= x) right = mid;
		else left = mid + 1;
	}
	return left;
}
int main()
{
	cin >> m >> n;
	for (int i = 1; i <= m; i++) cin >> a[i];
	sort(a + 1, a + 1 + m);
	// 加上左右护法
	a[0] = -1e7 + 10;
	LL ret = 0;
	for (int i = 1; i <= n; i++)
	{
		LL b; cin >> b;
		int pos = find(b);
		ret += min(abs(a[pos] - b), abs(a[pos - 1] - b));
	}
	cout << ret << endl;
	return 0;
}

7.2 ⼆分答案

7.2.1 ⽊材加⼯

牛客网链接


代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL n, k;
LL a[N];
// 当切割⻓度为 x 的时候，最多能切出来多少段
LL calc(LL x)
{
	LL cnt = 0;
	for (int i = 1; i <= n; i++)
	{
		cnt += a[i] / x;
	}
	return cnt;
}
int main()
{
	cin >> n >> k;
	for (int i = 1; i <= n; i++) cin >> a[i];
	LL left = 0, right = 1e8;
	while (left < right)
	{
		LL mid = (left + right + 1) / 2;
		if (calc(mid) >= k) left = mid;
		else right = mid - 1;
	}
	cout << left << endl;
	return 0;
}

7.2.2 砍树

牛客网链接


代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10;
LL n, m;
LL a[N];
// 当伐⽊机的⾼度为 x 时，所能获得的⽊材
LL calc(LL x)
{
    LL ret = 0;
    for (int i = 1; i <= n; i++)
    {
        if (a[i] > x) ret += a[i] - x;
    }
    return ret;
}
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> a[i];
    LL left = 1, right = 2e9;
    while (left < right)
    {
        LL mid = (left + right + 1) / 2;
        if (calc(mid) >= m) left = mid;
        else right = mid - 1;
    }
    cout << left << endl;
    return 0;
}

7.2.3 跳⽯头

牛客网链接


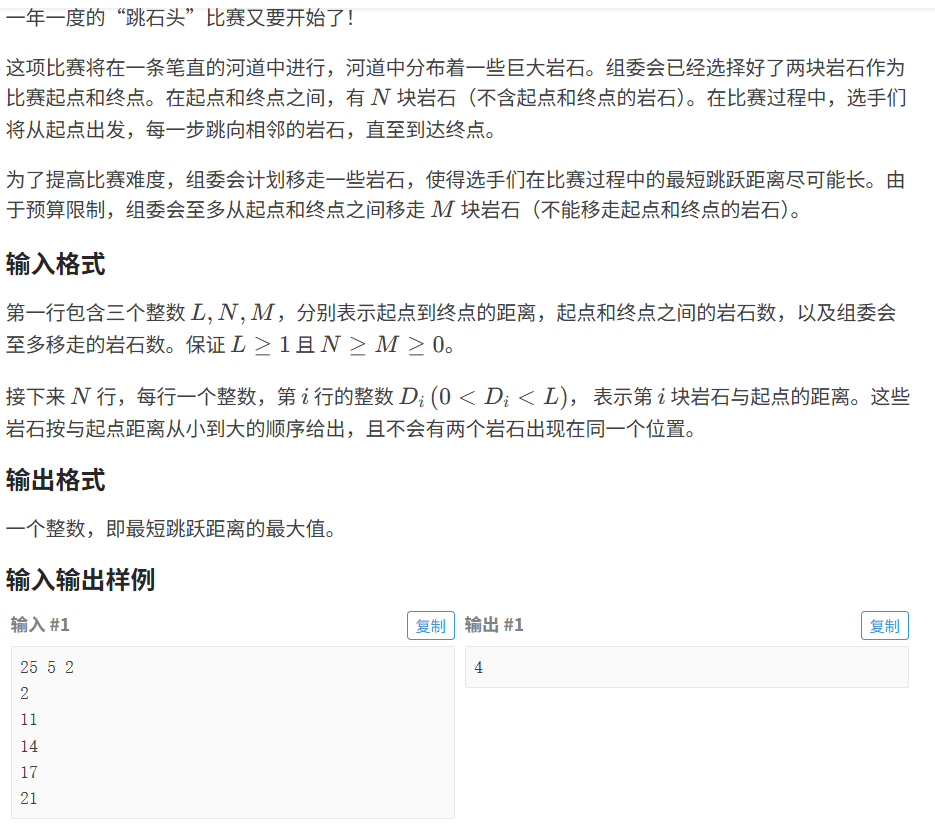
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 5e4 + 10;
LL l, n, m;
LL a[N];
// 当最短跳跃距离为 x 时，移⾛的岩⽯数⽬
LL calc(LL x)
{
	LL ret = 0;
	for (int i = 0; i <= n; i++)
	{
		int j = i + 1;
		while (j <= n && a[j] - a[i] < x) j++;
		ret += j - i - 1;
		i = j - 1;
	}
	return ret;
}
int main()
{
	cin >> l >> n >> m;
	for (int i = 1; i <= n; i++) cin >> a[i];
	a[n + 1] = l;
	n++;
	LL left = 1, right = l;
	while (left < right)
	{
		LL mid = (left + right + 1) / 2;
		if (calc(mid) <= m) left = mid;
		else right = mid - 1;
	}
	cout << left << endl;
	return 0;
}

整体源代码

代码如下（示例）：

c 复制代码 
//#include <iostream>
//#include <cmath>
//using namespace std;
//int main()
//{
//    int n; cin >> n;
//    // 循环次数
//    for (int i = n; i >= 0; i--)
//    {
//        int a; cin >> a;
//        if (a == 0) continue; // 处理系数为 0 的情况
//        // 1. 符号
//        if (a < 0) cout << '-';
//        else
//        {
//            if (i != n) cout << '+';
//        }
//        // 2. 数字
//        a = abs(a);
//        if (a != 1 || (a == 1 && i == 0)) cout << a;
//        // 3. 次数
//        if (i == 0) continue;
//        else if (i == 1) cout << 'x';
//        else cout << "x^" << i;
//    }
//    return 0;
//}




//#include<iostream>
//using namespace std;
//
//int dx[4] = { 0 , 1 , 0 , -1 };
//int dy[4] = { 1 , 0 ,-1 ,  0 };
//const int N = 15;
//int arr[N][N];
//
//int main()
//{
//	int n; cin >> n;
//	int cnt = 1;
//	int pos = 0;
//	int x = 1, y = 1;
//	while (cnt <= n * n)
//	{
//		arr[x][y] = cnt;
//		int a = x + dx[pos], b = y + dy[pos];
//		if (a < 1 || a > n || b < 1 || b > n || arr[a][b])
//		{
//			pos = (pos + 1) % 4;
//			a = x + dx[pos], b = y + dy[pos];
//		}
//		x = a, y = b;
//		cnt++;
//	}
//	for (int i = 1; i <= n; i++)
//	{
//		for (int j = 1; j <= n; j++)
//		{
//			printf("%3d", arr[i][j]);
//		}
//		puts("");
//	}
//}




//#include <iostream>
//#include<string>
//#include <algorithm>
//using namespace std;
//int p1, p2, p3, n;
//string s;
//string ret;
//// 判断是否是数字字符
//bool isdig(char ch)
//{
//	return ch >= '0' && ch <= '9';
//}
//// 判断是否是⼩写字⺟
//bool islet(char ch)
//{
//	return ch >= 'a' && ch <= 'z';
//}
//// 把 [left, right] 之间的字符展开
//// left, right 这两个字符是不做处理
//void add(char left, char right)
//{
//	string t;
//	// 遍历中间的字符
//	for (char ch = left + 1; ch < right; ch++)
//	{
//		char tmp = ch;
//		// 处理 p1
//		if (p1 == 2 && islet(tmp)) tmp -= 32; // ⼩写变⼤写
//		else if (p1 == 3) tmp = '*'; // 变成星号
//		// 处理 p2
//		for (int i = 0; i < p2; i++)
//		{
//			t += tmp;
//		}
//	}
//	// 处理 p3
//	if (p3 == 2) reverse(t.begin(), t.end());
//	ret += t;
//}
//int main()
//{
//	cin >> p1 >> p2 >> p3 >> s;
//	n = s.size();
//	for (int i = 0; i < n; i++)
//	{
//		char ch = s[i];
//		if (s[i] != '-' || i == 0 || i == n - 1) ret += ch;
//		else
//		{
//			char left = s[i - 1], right = s[i + 1];
//			// 判断是否展开
//			if (isdig(left) && isdig(right) && right > left ||
//				islet(left) && islet(right) && right > left)
//			{
//				// 展开
//				add(left, right);
//			}
//			else
//			{
//				ret += ch;
//			}
//		}
//	}
//	cout << ret << endl;
//	return 0;
//}


//#include<iostream>
//#include<string>
//using namespace std;
//const int N = 1e6 + 10;
//int a[N], b[N], c[N];
//int la, lb, lc;
//string x, y;
//
//void add(int a[], int b[], int c[])
//{
//	for (int i = 0; i < lc; i++)
//	{
//		c[i] += a[i] + b[i];
//		c[i + 1] += c[i] / 10;
//		c[i] %= 10;
//	}
//	if (c[lc]) lc++;
//}
//int main()
//{
//	cin >> x >> y;
//	la = x.size(), lb = y.size(), lc = max(la, lb);
//	for (int i = 0; i < la; i++) a[la - 1 - i] = x[i] - '0';
//	for (int i = 0; i < lb; i++) b[lb - 1 - i] = y[i] - '0';
//	add(c, a, b);
//	for (int i = lc - 1; i >= 0; i--) cout << c[i];
//}




//#include <iostream>
//using namespace std;
//const int N = 1e6 + 10;
//int a[N], b[N], c[N];
//int la, lb, lc;
//// ⾼精度加法的模版 - c = a + b;
//void add(int c[], int a[], int b[])
//{
//	for (int i = 0; i < lc; i++)
//	{
//		c[i] += a[i] + b[i]; // 对应位相加，再加上进位
//		c[i + 1] += c[i] / 10; // 处理进位
//		c[i] %= 10; // 处理余数
//	}
//	if (c[lc]) lc++;
//}
//int main()
//{
//	string x, y; cin >> x >> y;
//	// 1. 拆分每⼀位，逆序放在数组中
//	la = x.size(); lb = y.size(); lc = max(la, lb);
//	for (int i = 0; i < la; i++) a[la - 1 - i] = x[i] - '0';
//	for (int i = 0; i < lb; i++) b[lb - 1 - i] = y[i] - '0';
//	// 2. 模拟加法的过程
//	add(c, a, b); // c = a + b
//	// 输出结果
//	for (int i = lc - 1; i >= 0; i--) cout << c[i];
//	return 0;
//}


//#include <iostream>
//using namespace std;
//const int N = 1e6 + 10;
//int a[N], b[N], c[N];
//int la, lb, lc;
//// ⽐⼤⼩
//bool cmp(string& x, string& y)
//{
//	// 先⽐较⻓度
//	if (x.size() != y.size()) return x.size() < y.size();
//	// 再按照 字典序 的⽅式⽐较
//	return x < y;
//}
//// ⾼精度减法的模板 - c = a - b
//void sub(int c[], int a[], int b[])
//{
//	for (int i = 0; i < lc; i++)
//	{
//		c[i] += a[i] - b[i]; // 对应位相减，然后处理借位
//		if (c[i] < 0)
//		{
//			c[i + 1] -= 1; // 借位
//			c[i] += 10;
//		}
//	}
//	// 处理前导零
//	while (lc > 1 && c[lc - 1] == 0) lc--;
//}
//int main()
//{
//	string x, y; cin >> x >> y;
//	// ⽐⼤⼩
//	if (cmp(x, y))
//	{
//		swap(x, y);
//		cout << '-';
//	}
//	// 1. 拆分每⼀位，然后逆序放在数组中
//	la = x.size(); lb = y.size(); lc = max(la, lb);
//	for (int i = 0; i < la; i++) a[la - i - 1] = x[i] - '0';
//	for (int i = 0; i < lb; i++) b[lb - i - 1] = y[i] - '0';
//	// 2. 模拟减法的过程
//	sub(c, a, b); // c = a - b
//	// 输出结果
//	for (int i = lc - 1; i >= 0; i--) cout << c[i];
//	return 0;
//}


//#include <iostream>
//using namespace std;
//const int N = 1e6 + 10;
//int a[N], b[N], c[N];
//int la, lb, lc;
//// ⾼精度乘法的模版 - c = a * b
//void mul(int c[], int a[], int b[])
//{
//	// ⽆进位相乘,然后相加
//	for (int i = 0; i < la; i++)
//	{
//		for (int j = 0; j < lb; j++)
//		{
//			c[i + j] += a[i] * b[j];
//		}
//	}
//	// 处理进位
//	for (int i = 0; i < lc; i++)
//	{
//		c[i + 1] += c[i] / 10;
//		c[i] %= 10;
//	}
//	// 处理前导零
//	while (lc > 1 && c[lc - 1] == 0) lc--;
//}
//int main()
//{
//	string x, y; cin >> x >> y;
//	// 1. 拆分每⼀位，逆序放在数组中
//	la = x.size(); lb = y.size(); lc = la + lb;
//	for (int i = 0; i < la; i++) a[la - 1 - i] = x[i] - '0';
//	for (int i = 0; i < lb; i++) b[lb - 1 - i] = y[i] - '0';
//	// 2. 模拟乘法的过程
//	mul(c, a, b); // c = a * b
//	// 输出结果
//	for (int i = lc - 1; i >= 0; i--) cout << c[i];
//	return 0;
//}



//#include<iostream>
//using namespace std;
//const int N = 1e6 + 10;
//typedef long long LL;
//int a[N], b, c[N];
//int la, lc;
//// ⾼精度除法的模板 - c = a / b （⾼精度 / 低精度）
//void sub(int c[], int a[], int b)
//{
//	LL t = 0; // 标记每次除完之后的余数
//	for (int i = la - 1; i >= 0; i--)
//	{
//		// 计算当前的被除数
//		t = t * 10 + a[i];
//		c[i] = t / b;
//		t %= b;
//	}
//	// 处理前导 0
//	while (lc > 1 && c[lc - 1] == 0) lc--;
//}
//int main()
//{
//	string x; cin >> x >> b;
//	la = x.size();
//	for (int i = 0; i < la; i++) a[la - 1 - i] = x[i] - '0';
//	// 模拟除法的过程
//	lc = la;
//	sub(c, a, b); // c = a / b
//	for (int i = lc - 1; i >= 0; i--) cout << c[i];
//	return 0;
//}


//#include<iostream>
//using namespace std;
//int n;
//const int N = 5;
//int a[N], b[N], c[N], d[N];
//int x, y;
//
//int find()
//{
//	for (int i = n; i >=1 ; i--)
//	{
//		if (a[i] <= x && b[i] <= y && a[i] + c[i] >= x && b[i] + d[i] >= y)
//		{
//			return i;
//		}
//		return -1;
//	}
//}
//int main()
//{
//	cin >> n;
//	for (int i = 1; i <= n; i++) cin >> a[i] >> b[i] >> c[i] >> d[i];
//	cin >> x >> y;
//	cout << find() << endl;
//}


//#include <iostream>
//using namespace std;
//const int N = 1e4 + 10;
//int n;
//int a[N], b[N], g[N], k[N];
//int x, y;
//int find()
//{
//	// 从后往前枚举
//	for (int i = n; i >= 1; i--)
//	{
//		// 判断是否覆盖
//		if (a[i] <= x && b[i] <= y && a[i] + g[i] >= x && b[i] + k[i] >= y)
//		{
//			return i;
//		}
//	}
//	return -1;
//}
//int main()
//{
//	cin >> n;
//	for (int i = 1; i <= n; i++) cin >> a[i] >> b[i] >> g[i] >> k[i];
//	cin >> x >> y;
//	cout << find() << endl;
//	return 0;
//}


//#include <iostream>
//using namespace std;
//int x, y;
//int day[] = { 0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31 };
//int main()
//{
//	cin >> x >> y;
//	int ret = 0;
//	// 枚举⽉⽇的组合
//	for (int i = 1; i <= 12; i++)
//	{
//		for (int j = 1; j <= day[i]; j++)
//		{
//			int k = j % 10 * 1000 + j / 10 * 100 + i % 10 * 10 + i / 10;
//			int num = k * 10000 + i * 100 + j;
//			if (x <= num && num <= y) ret++;
//		}
//	}
//	cout << ret << endl;
//	return 0;
//}


//#include <iostream>
//using namespace std;
//const int N = 1e4 + 10;
//int n;
//int a[N], b[N];
//// 不放地雷
//int check1()
//{
//	a[1] = 0;
//	for (int i = 2; i <= n + 1; i++)
//	{
//		a[i] = b[i - 1] - a[i - 1] - a[i - 2];
//		if (a[i] < 0 || a[i] > 1) return 0;
//	}
//	if (a[n + 1] == 0) return 1;
//	else return 0;
//}
//int check2()
//{
//	a[1] = 1;
//	for (int i = 2; i <= n + 1; i++)
//	{
//		a[i] = b[i - 1] - a[i - 1] - a[i - 2];
//		if (a[i] < 0 || a[i] > 1) return 0;
//	}
//	if (a[n + 1] == 0) return 1;
//	else return 0;
//}
//int main()
//{
//	cin >> n;
//	for (int i = 1; i <= n; i++) cin >> b[i];
//	int ret = 0;
//	ret += check1(); // a[1] 不放地雷
//	ret += check2(); // a[1] 放地雷
//	cout << ret << endl;
//	return 0;
//}


//class Solution
//{
//public:
//	vector<vector<int>> subsets(vector<int>& nums)
//	{
//		vector<vector<int>> ret;
//		int n = nums.size();
//		// 枚举所有的状态
//		for (int st = 0; st < (1 << n); st++)
//		{
//			// 根据 st 的状态，还原出要选的数
//			vector<int> tmp; // 从当前选的⼦集
//			for (int i = 0; i < n; i++)
//			{
//				if ((st >> i) & 1) tmp.push_back(nums[i]);
//			}
//			ret.push_back(tmp);
//		}
//		return ret;
//	}
//};




//#include <iostream>
//#include <cstring>
//using namespace std;
//const int N = 10;
//int n = 5;
//int a[N]; // ⽤⼆进制表⽰，来存储灯的状态
//int t[N]; // 备份 a 数组
//// 计算 x 的⼆进制表⽰中⼀共有多少个 1
//int calc(int x)
//{
//	int cnt = 0;
//	while (x)
//	{
//		cnt++;
//		x &= x - 1;
//	}
//	return cnt;
//}
//int main()
//{
//	int T; cin >> T;
//	while (T--)
//	{
//		// 多组测试时，⼀定要注意清空之前的数据
//		memset(a, 0, sizeof a);
//		for (int i = 0; i < n; i++)
//		{
//			for (int j = 0; j < n; j++)
//			{
//				char ch; cin >> ch;
//				// 存成相反的
//				if (ch == '0') a[i] |= 1 << j;
//			}
//		}
//		int ret = 0x3f3f3f3f; // 统计所有合法的按法中的最⼩值
//		// 枚举第⼀⾏所有的按法
//		for (int st = 0; st < (1 << n); st++)
//		{
//			memcpy(t, a, sizeof a);
//			int push = st; // 当前⾏的按法
//			int cnt = 0; // 统计当前按法下⼀共按了多少次
//			// 依次计算后续⾏的结果以及按法
//			for (int i = 0; i < n; i++)
//			{
//				cnt += calc(push);
//				// 修改当前⾏被按的结果
//				t[i] = t[i] ^ push ^ (push << 1) ^ (push >> 1);
//				t[i] &= (1 << n) - 1; // 清空影响
//				// 修改下⼀⾏的状态
//				t[i + 1] ^= push;
//				// 下⼀⾏的按法
//				push = t[i];
//			}
//			if (t[n - 1] == 0) ret = min(ret, cnt);
//		}
//		if (ret > 6) cout << -1 << endl;
//		else cout << ret << endl;
//	}
//	return 0;
//}



//#include <iostream>
//#include <cstring>
//using namespace std;
//const int N = 20;
//int n;
//int a[N]; // ⽤⼆进制存储状态
//int t[N]; // 备份
//// 判断 x->y 是否合法
//// 返回 -1，表⽰不合法
//// 其余的数，表⽰合法，并且表⽰ 0->1 的次数
//int calc(int x, int y)
//{
//	int sum = 0;
//	for (int i = 0; i < n; i++)
//	{
//		if (((x >> i) & 1) == 0 && ((y >> i) & 1) == 1) sum++;
//		if (((x >> i) & 1) == 1 && ((y >> i) & 1) == 0) return -1;
//	}
//	return sum;
//}
//int solve()
//{
//	int ret = 0x3f3f3f3f; // 记录最⼩的改变次数
//	// 枚举第⼀⾏的最终状态
//	for (int st = 0; st < (1 << n); st++)
//	{
//		memcpy(t, a, sizeof a);
//		int change = st;
//		int cnt = 0; // 统计 0->1 的次数
//		bool flag = 1;
//		for (int i = 1; i <= n; i++)
//		{
//			// 先判断 change 是否合法
//			int c = calc(t[i], change);
//			if (c == -1)
//			{
//				flag = 0;
//				break;
//			}
//			cnt += c; // 累加次数
//			// 当前⾏的最终状态
//			t[i] = change;
//			// 计算下⼀⾏的最终状态
//			change = t[i - 1] ^ (t[i] << 1) ^ (t[i] >> 1);
//			change &= (1 << n) - 1;
//		}
//		if (flag) ret = min(ret, cnt);
//	}
//	if (ret == 0x3f3f3f3f) return -1;
//	else return ret;
//}
//int main()
//{
//	int T; cin >> T;
//	for (int k = 1; k <= T; k++)
//	{
//		// 多组测试数据，记得清空
//		memset(a, 0, sizeof a);
//		cin >> n;
//		for (int i = 1; i <= n; i++) // 避免越界访问
//		{
//			for (int j = 0; j < n; j++)
//			{
//				int x; cin >> x;
//				if (x) a[i] |= 1 << j;
//			}
//		}
//		printf("Case %d: %d\n", k, solve());
//	}
//	return 0;
//}


//#include <iostream>
//using namespace std;
//typedef long long LL;
//const int N = 1e5 + 10;
//int n, q;
//LL a[N];
//LL f[N]; // 前缀和数组
//int main()
//{
//	cin >> n >> q;
//	for (int i = 1; i <= n; i++) cin >> a[i];
//	// 处理前缀和数组
//	for (int i = 1; i <= n; i++)
//	{
//		f[i] = f[i - 1] + a[i];
//	}
//	// 处理 q 次询问
//	while (q--)
//	{
//		int l, r; cin >> l >> r;
//		cout << f[r] - f[l - 1] << endl;
//	}
//	return 0;
//}


//#include<iostream>
//using namespace std;
//int n, x;
//const int N = 2e5 + 10;
//int f[N];
//
//int main()
//{
//	cin >> n;
//	for (int i = 1; i <= n; i++)
//	{
//		cin >> x;
//		f[i] = f[i - 1] + x;
//	}
//	int ret = -0x3f3f3f3f;
//	int prevmin = 0;
//	for (int i = 1; i <= n; i++)
//	{
//		ret = max(ret, f[i] - prevmin);
//		prevmin = min(prevmin, f[i]);
//	}
//	cout << ret << endl;
// }



//#include <iostream>
//using namespace std;
//typedef long long LL;
//const int N = 1010;
//int n, m, q;
//LL f[N][N];
//int main()
//{
//	cin >> n >> m >> q;
//	// 预处理前缀和矩阵
//	for (int i = 1; i <= n; i++)
//	{
//		for (int j = 1; j <= m; j++)
//		{
//			LL x; cin >> x;
//			f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + x;
//		}
//	}
//	// 处理 q 次查询
//	while (q--)
//	{
//		int x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2;
//		cout << f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1]
//			<< endl;
//	}
//	return 0;
//}




//#include <iostream>
//using namespace std;
//const int N = 5010;
//int n, m;
//int a[N][N];
//int f[N][N]; // 前缀和矩阵
//int main()
//{
//	cin >> n >> m;
//	while (n--)
//	{
//		int x, y, v; cin >> x >> y >> v;
//		x++, y++; // 下标从 1 开始计数
//		a[x][y] += v; // 同⼀个位置有可能有多个⽬标
//	}
//	n = 5001;
//	// 预处理前缀和矩阵
//	for (int i = 1; i <= n; i++)
//	{
//		for (int j = 1; j <= n; j++)
//		{
//			f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + a[i][j];
//		}
//	}
//	int ret = 0;
//	m = min(m, n); // 如果 m 很⼤，相当于就是把整个区域全部摧毁
//	// 枚举所有边⻓为 m 的正⽅形
//	for (int x2 = m; x2 <= n; x2++)
//	{
//		for (int y2 = m; y2 <= n; y2++)
//		{
//			int x1 = x2 - m + 1, y1 = y2 - m + 1;
//			ret = max(ret, f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 -
//				1][y1 - 1]);
//		}
//	}
//	cout << ret << endl;
//	return 0;
//}




//#include <iostream>
//using namespace std;
//typedef long long LL;
//const int N = 1e5 + 10;
//int n, m;
//LL f[N]; // 差分数组
//int main()
//{
//	cin >> n >> m;
//	// 利⽤差分数组的性质，创建差分数组
//	for (int i = 1; i <= n; i++)
//	{
//		LL x; cin >> x;
//		f[i] += x;
//		f[i + 1] -= x;
//	}
//	// 处理 m 次修改操作
//	while (m--)
//	{
//		LL l, r, k; cin >> l >> r >> k;
//		f[l] += k; f[r + 1] -= k;
//	}
//	// 还原出原始的数组
//	for (int i = 1; i <= n; i++)
//	{
//		f[i] = f[i - 1] + f[i];
//		cout << f[i] << " ";
//	}
//	return 0;
//}


//#include <iostream>
//using namespace std;
//typedef long long LL;
//const int N = 1e5 + 10;
//int n, m;
//LL f[N]; // 差分数组
//int main()
//{
//	cin >> n >> m;
//	// x->y
//	int x; cin >> x;
//	for (int i = 2; i <= m; i++)
//	{
//		int y; cin >> y;
//		// x -> y
//		if (x > y)
//		{
//			f[y]++;
//			f[x]--;
//		}
//		else
//		{
//			f[x]++;
//			f[y]--;
//		}
//		x = y;
//	}
//	// 利⽤差分数组，还原出原数组
//	for (int i = 1; i <= n; i++) f[i] += f[i - 1];
//	// 直接求结果
//	LL ret = 0;
//	for (int i = 1; i < n; i++)
//	{
//		LL a, b, c; cin >> a >> b >> c;
//		ret += min(a * f[i], c + b * f[i]);
//	}
//	cout << ret << endl;
//	return 0;
//}




//#include <iostream>
//using namespace std;
//typedef long long LL;
//const int N = 1010;
//int n, m, q;
//LL f[N][N]; // 差分矩阵
//// 差分矩阵的性质
//void insert(int x1, int y1, int x2, int y2, LL k)
//{
//	f[x1][y1] += k; f[x1][y2 + 1] -= k; f[x2 + 1][y1] -= k; f[x2 + 1][y2 + 1]
//		+= k;
//}
//int main()
//{
//	cin >> n >> m >> q;
//	// 预处理差分矩阵
//	for (int i = 1; i <= n; i++)
//	{
//		for (int j = 1; j <= m; j++)
//		{
//			LL x; cin >> x;
//			// [i, j]为左上⻆，[i, j]为右下⻆的矩阵，统⼀加上 x
//			insert(i, j, i, j, x);
//		}
//	}
//	// 处理 q 次修改操作
//	while (q--)
//	{
//		LL x1, y1, x2, y2, k; cin >> x1 >> y1 >> x2 >> y2 >> k;
//		insert(x1, y1, x2, y2, k);
//	}
//	// 利⽤前缀和还原出修改之后的数组
//	for (int i = 1; i <= n; i++)
//	{
//		for (int j = 1; j <= m; j++)
//		{
//			f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + f[i][j];
//			cout << f[i][j] << " ";
//		}
//		cout << endl;
//	}
//	return 0;
//}



//#include <iostream>
//using namespace std;
//const int N = 1010;
//int n, m;
//int f[N][N]; // 差分矩阵
//// 差分数组的性质
//void insert(int x1, int y1, int x2, int y2, int k)
//{
//	f[x1][y1] += k; f[x1][y2 + 1] -= k; f[x2 + 1][y1] -= k; f[x2 + 1][y2 + 1]
//		+= k;
//}
//int main()
//{
//	cin >> n >> m;
//	// 构建差分数组
//	while (m--)
//	{
//		int x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2;
//		insert(x1, y1, x2, y2, 1);
//	}
//	// 利⽤前缀和还原修改之后的数组
//	for (int i = 1; i <= n; i++)
//	{
//		for (int j = 1; j <= n; j++)
//		{
//			f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + f[i][j];
//			cout << f[i][j] << " ";
//		}
//		cout << endl;
//	}
//	return 0;
//}


//#include <iostream>
//#include <unordered_map>
//using namespace std;
//const int N = 1e6 + 10;
//int n;
//int a[N];
//int main()
//{
//	int T; cin >> T;
//	while (T--)
//	{
//		cin >> n;
//		for (int i = 1; i <= n; i++) cin >> a[i];
//		// 初始化
//		int left = 1, right = 1, ret = 0;
//		unordered_map<int, int> mp; // 维护窗⼝内所有元素出现的次数
//		while (right <= n)
//		{
//			// 进窗⼝
//			mp[a[right]]++;
//			// 判断
//			while (mp[a[right]] > 1)
//			{
//				// 出窗⼝
//				mp[a[left]]--;
//				left++;
//			}
//			// 窗⼝合法，更新结果
//			ret = max(ret, right - left + 1);
//			right++;
//		}
//		cout << ret << endl;
//	}
//	return 0;
//}


//#include<iostream>
//using namespace std;
//const int N = 1e6 + 10, M = 2e3 + 10;
//int n, m;
//int a[N];
//int kind; // 窗⼝内有效元素的个数
//int mp[N]; // 统计窗⼝内每个元素出现的次数
//int main()
//{
//	cin >> n >> m;
//	for (int i = 1; i <= n; i++) cin >> a[i];
//	int left = 1, right = 1;
//	int ret = n, begin = 1;
//	while (right <= n)
//	{
//		// 进窗⼝
//		if (mp[a[right]]++ == 0) kind++;
//		// 判断
//		while (kind == m)
//		{
//			// 更新结果
//			int len = right - left + 1;
//			if (len < ret)
//			{
//				ret = len;
//				begin = left;
//			}
//			// 出窗⼝
//			if (mp[a[left]]-- == 1) kind--;
//			left++;
//		}
//		right++;
//	}
//	cout << begin << " " << begin + ret - 1 << endl;
//	return 0;
//}


//#include <iostream>
//using namespace std;
//string s;
//int mp[26]; // 统计每个⼩写字符出现的次数
//int kind; // 窗⼝内⼩写字符的种类
//int main()
//{
//	cin >> s;
//	int n = s.size();
//	int ret = n;
//	// 初始化
//	for (int left = 0, right = 0; right < n; right++)
//	{
//		// 进窗⼝
//		if (mp[s[right] - 'a']++ == 0) kind++;
//		// 判断
//		while (kind == 26)
//		{
//			// 更新结果
//			ret = min(ret, right - left + 1);
//			// 出窗⼝
//			if (mp[s[left] - 'a']-- == 1) kind--;
//			left++;
//		}
//	}
//	cout << ret << endl;
//	return 0;
//}



//#include<iostream>
//using namespace std;
//typedef long long LL;
//const int N = 1e5 + 10;
//int n;
//LL a[N];
//int main()
//{
//	cin >> n;
//	LL sum = 0;
//	for (int i = 1; i <= n; i++)
//	{
//		cin >> a[i];
//		sum += a[i];
//	}
//	int left = 1, right = 1;
//	LL k = 0;
//	LL ret = 0;
//	while (right <= n)
//	{
//		k += a[right];
//		while (2 * k >= sum)
//		{
//			// ⽤ sum - k 来更新结果
//			ret = max(ret, sum - k);
//			k -= a[left++];
//		}
//		// ⽤ k 来更新结果
//		ret = max(ret, k);
//		right++;
//	}
//	cout << ret << endl;
//	return 0;
//}



//#include <iostream>
//using namespace std;
//const int N = 1e5 + 10;
//int n;
//int a[N];
//int binary_search(int x, int y)
//{
//	// ⼤于等于 x 的最⼩元素
//	int left = 1, right = n;
//	while (left < right)
//	{
//		int mid = (left + right) / 2;
//		if (a[mid] >= x) right = mid;
//		else left = mid + 1;
//	}
//	if (a[left] < x) return 0;
//	int tmp = left;
//	// ⼩于等于 y 的最⼤元素
//	left = 1, right = n;
//	while (left < right)
//	{
//		int mid = (left + right + 1) / 2;
//		if (a[mid] <= y) left = mid;
//		else right = mid - 1;
//	}
//	if (a[left] > y) return 0;
//	return left - tmp + 1;
//}
//int main()
//{
//	cin >> n;
//	for (int i = 1; i <= n; i++) cin >> a[i];
//	int Q; cin >> Q;
//	while (Q--)
//	{
//		int x, y; cin >> x >> y;
//		cout << binary_search(x, y) << endl;
//	}
//	return 0;
//}


//#include <iostream>
//#include <algorithm>
//using namespace std;
//typedef long long LL;
//const int N = 2e5 + 10;
//LL n, c;
//LL a[N];
//int main()
//{
//	cin >> n >> c;
//	for (int i = 1; i <= n; i++) cin >> a[i];
//	sort(a + 1, a + 1 + n);
//	LL ret = 0;
//	for (int i = 2; i <= n; i++)
//	{
//		// a[i]
//		LL b = a[i] - c;
//		ret += upper_bound(a + 1, a + i, b) - lower_bound(a + 1, a + i, b);
//	}
//	cout << ret << endl;
//	return 0;
//}


//#include <iostream>
//#include <algorithm>
//using namespace std;
//typedef long long LL;
//const int N = 1e5 + 10;
//int n, m;
//LL a[N];
//int find(LL x)
//{
//	int left = 1, right = m;
//	while (left < right)
//	{
//		int mid = (left + right) / 2;
//		if (a[mid] >= x) right = mid;
//		else left = mid + 1;
//	}
//	return left;
//}
//int main()
//{
//	cin >> m >> n;
//	for (int i = 1; i <= m; i++) cin >> a[i];
//	sort(a + 1, a + 1 + m);
//	// 加上左右护法
//	a[0] = -1e7 + 10;
//	LL ret = 0;
//	for (int i = 1; i <= n; i++)
//	{
//		LL b; cin >> b;
//		int pos = find(b);
//		ret += min(abs(a[pos] - b), abs(a[pos - 1] - b));
//	}
//	cout << ret << endl;
//	return 0;
//}


//#include <iostream>
//using namespace std;
//typedef long long LL;
//const int N = 1e5 + 10;
//LL n, k;
//LL a[N];
//// 当切割⻓度为 x 的时候，最多能切出来多少段
//LL calc(LL x)
//{
//	LL cnt = 0;
//	for (int i = 1; i <= n; i++)
//	{
//		cnt += a[i] / x;
//	}
//	return cnt;
//}
//int main()
//{
//	cin >> n >> k;
//	for (int i = 1; i <= n; i++) cin >> a[i];
//	LL left = 0, right = 1e8;
//	while (left < right)
//	{
//		LL mid = (left + right + 1) / 2;
//		if (calc(mid) >= k) left = mid;
//		else right = mid - 1;
//	}
//	cout << left << endl;
//	return 0;
//}


//#include <iostream>
//using namespace std;
//typedef long long LL;
//const int N = 1e6 + 10;
//LL n, m;
//LL a[N];
//// 当伐⽊机的⾼度为 x 时，所能获得的⽊材
//LL calc(LL x)
//{
//    LL ret = 0;
//    for (int i = 1; i <= n; i++)
//    {
//        if (a[i] > x) ret += a[i] - x;
//    }
//    return ret;
//}
//int main()
//{
//    cin >> n >> m;
//    for (int i = 1; i <= n; i++) cin >> a[i];
//    LL left = 1, right = 2e9;
//    while (left < right)
//    {
//        LL mid = (left + right + 1) / 2;
//        if (calc(mid) >= m) left = mid;
//        else right = mid - 1;
//    }
//    cout << left << endl;
//    return 0;
//}


//#include <iostream>
//using namespace std;
//typedef long long LL;
//const int N = 5e4 + 10;
//LL l, n, m;
//LL a[N];
//// 当最短跳跃距离为 x 时，移⾛的岩⽯数⽬
//LL calc(LL x)
//{
//	LL ret = 0;
//	for (int i = 0; i <= n; i++)
//	{
//		int j = i + 1;
//		while (j <= n && a[j] - a[i] < x) j++;
//		ret += j - i - 1;
//		i = j - 1;
//	}
//	return ret;
//}
//int main()
//{
//	cin >> l >> n >> m;
//	for (int i = 1; i <= n; i++) cin >> a[i];
//	a[n + 1] = l;
//	n++;
//	LL left = 1, right = l;
//	while (left < right)
//	{
//		LL mid = (left + right + 1) / 2;
//		if (calc(mid) <= m) left = mid;
//		else right = mid - 1;
//	}
//	cout << left << endl;
//	return 0;
//}
相关推荐
小年糕是糕手2 小时前
【数据结构】常见的排序算法 -- 选择排序
linux·数据结构·c++·算法·leetcode·蓝桥杯·排序算法
电子_咸鱼3 小时前
动态规划经典题解：单词拆分（LeetCode 139）
java·数据结构·python·算法·leetcode·线性回归·动态规划
小安同学iter7 小时前
SQL50+Hot100系列（11.9）
算法·leetcode·职场和发展
炼金士8 小时前
基于多智能体技术的码头车辆最快行驶路径方案重构
算法·路径规划·集装箱码头
小刘max9 小时前
最长递增子序列（LIS）详解：从 dp[i] 到 O(n²) 动态规划
算法·动态规划
谢景行^顾10 小时前
数据结构知识掌握
linux·数据结构·算法
2351610 小时前
【JVM】Java为啥能跨平台？JDK/JRE/JVM的关系？
java·开发语言·jvm·spring boot·后端·spring·职场和发展
ShineWinsu10 小时前
对于数据结构:堆的超详细保姆级解析——下（堆排序以及TOP-K问题）
c语言·数据结构·c++·算法·面试·二叉树·堆
DuHz10 小时前
基于时频域霍夫变换的汽车雷达互干扰抑制——论文阅读
论文阅读·算法·汽车·毫米波雷达
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03综合整理：pdf预览显示：你尝试预览的文件可能对你的计算机有害。如果你信任此文件以及其来源，请打开此文件以看其内容，如何解决以正常预览文件04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05Linux下V2Ray安装配置指南06BongoCat - 跨平台键盘猫动画工具07Labelme从安装到标注：零基础完整指南08《大数据技术原理与应用》实验报告三 熟悉HBase常用操作09jdk21下载、安装（Windows、Linux、macOS）10NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南