2025.9.28华为软开

1.分布式系统任务调度

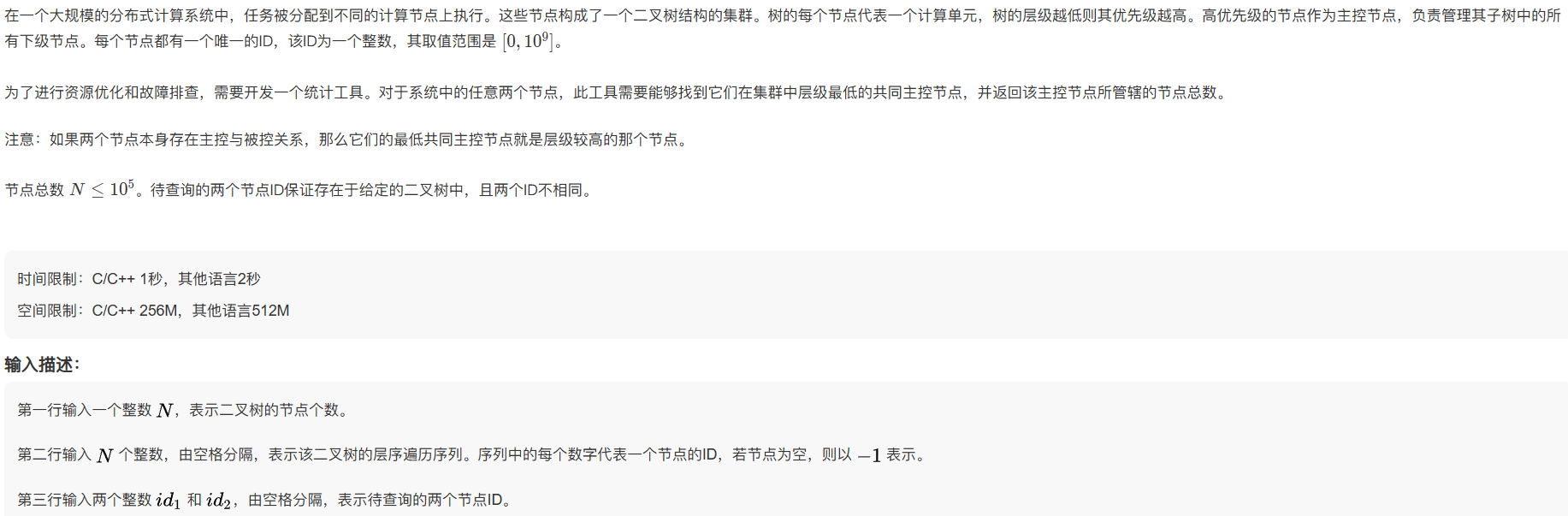
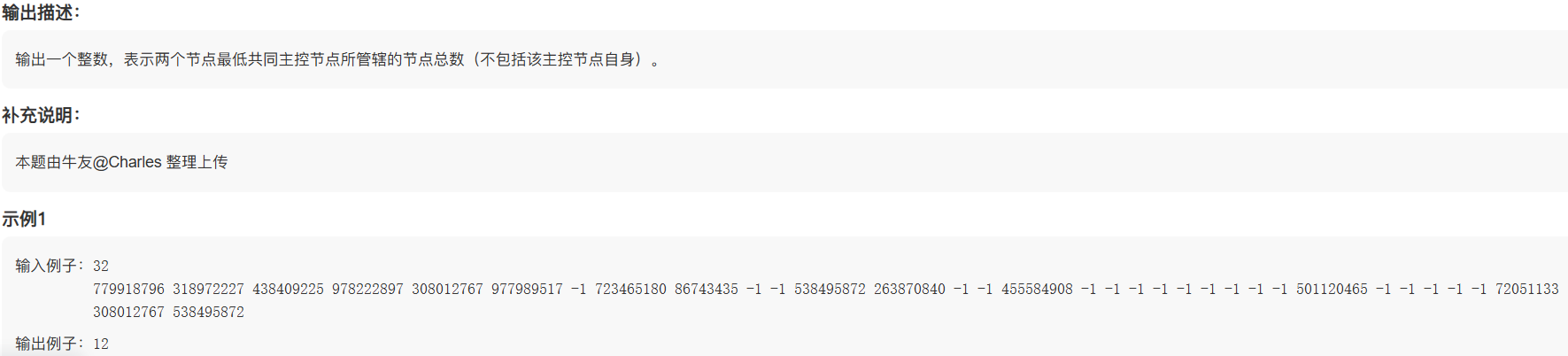
leetcode的寻找二叉树的公共祖先原题

java 复制代码

import java.util.Scanner;

public class Main {
    private static int[] tree;
    private static int commonRoot;

    private static boolean dfs(int i, int target1, int target2) {
        if (i >= tree.length || tree[i] == -1) {
            return false;
        }
        if (tree[i] == target1 || tree[i] == target2) {
            commonRoot = i;
            return true;
        }
        boolean findLeft = dfs(2 * i + 1, target1, target2);
        boolean findRight = dfs(2 * i + 2, target1, target2);
        if (findLeft && findRight) {
            commonRoot = i;
        }
        return findLeft || findRight;
    }

    private static int count(int i) {
        if (i >= tree.length || tree[i] == -1) {
            return 0;
        }
        return 1 + count(2 * i + 1) + count(2 * i + 2);
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        tree = new int[n];
        for (int i = 0; i < n; i++) {
            tree[i] = scanner.nextInt();
        }
        dfs(0, scanner.nextInt(), scanner.nextInt());
        System.out.println(count(commonRoot) - 1);
        scanner.close();
    }
}

2.云服务资源调度

输入例子：
复制代码
13
78 32 44 98 73 46 98 31 54 27 51 9 8
113
输出例子：
复制代码
7

这个问题本质上属于经典的 "装箱问题（Bin Packing Problem）" 的变种，是算法领域中非常经典的组合优化问题之一，用到的思路正是装箱问题中经典的贪心解法。

装箱问题的经典性

装箱问题的描述是：给定一系列物品，每个物品有体积，还有容量固定的箱子，要求用最少的箱子装下所有物品。它是NP 难问题（没有已知的多项式时间精确解法），因此实际中常用贪心策略来求近似解，而你这个云服务调度问题，只是把 "物品体积" 换成 "任务计算成本"、"箱子容量" 换成 "服务器最大容量"，核心完全一致。

思路对应装箱问题的经典贪心策略

用的是 **"最佳适应递减（Best Fit Decreasing, BFD）"** 策略：

"递减"：先把物品（任务）按体积（成本）降序排序（对应你先处理大任务）；
"最佳适应"：对每个物品，找能装下它且剩余空间最小的箱子（服务器）（对应你选剩余容量最小的服务器）。

这种策略是装箱问题中最经典、近似效果最好的贪心算法之一（近似比约为 1.22），在资源调度、容器打包、物流装箱等实际场景中被广泛应用。

所以，你这个问题的思路并非凭空设计，而是源于经典装箱问题的贪心解法，属于经典算法思路在实际场景中的具体应用。

java 复制代码

import java.util.*;

public class Main {
    public static void main(String[] args) {
        //1.输入任务数量，并输入每个任务消耗的资源
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        List<Integer> costs = new ArrayList<>(n);
        for (int i = 0; i < n; i++) {
            costs.add(scanner.nextInt());
        }
        //2.按照每个任务的消耗做降序排序
        costs.sort(Comparator.reverseOrder());
        //3.输入每个服务器的最大容量
        int capacity = scanner.nextInt();
        //4.servers存储每个服务器，每个值对应的是服务器已经占有的资源
        List<Integer> servers = new ArrayList<>();
        for (int cost : costs) {
            //4.1寻找最接近恰好沾满服务器资源的服务器编号
            int minRemaining = Integer.MAX_VALUE;
            int minIndex = -1;
            for (int i = 0; i < servers.size(); i++) {
                int server = servers.get(i);
                if (server >= cost && minRemaining > server) {
                    minRemaining = server;
                    minIndex = i;
                }
            }
            //4.2如果有能塞入当前任务的服务器则加入到当前服务器，没有则增加一台服务器
            if (minRemaining != Integer.MAX_VALUE) {
                servers.set(minIndex, minRemaining - cost);
            } else {
                servers.add(capacity - cost);
            }
        }
        System.out.println(servers.size());
        scanner.close();
    }
}

3.无线网络信号覆盖塔

这个问题的核心思路是状态压缩枚举 （利用信号塔数量少的特性）+预处理优化，具体拆解如下：

1. 问题分析与突破口

题目中明确信号塔总数不超过 11 个 ------ 这是关键！因为 11 个信号塔的激活组合只有 \(2^{11}=2048\) 种可能，完全可以枚举所有组合，找到最优解。

我们需要对每个激活组合（子集）计算两个指标：

总有效数据价值：所有居民区的价值按覆盖次数取整求和。
激活的信号塔数量：在总价值最大时，选数量最少的。

2. 核心步骤拆解

（1）预处理：收集关键信息并优化计算

分类网格元素 ：遍历网格，分离出居民区 （记录位置和数据价值）和信号塔（记录位置和信号半径）。
预计算居民区的覆盖掩码 ：对每个居民区，计算哪些信号塔能覆盖它（用位掩码 表示，比如第 t 位为 1 表示第t个信号塔能覆盖该居民区）。这样后续计算覆盖次数时，只需通过位运算快速统计，无需重复遍历信号塔。

（2）枚举所有信号塔激活组合

对每一种激活组合（用整数mask表示，二进制位为 1 表示对应信号塔激活）：

计算该组合激活的信号塔数量（mask的二进制中 1 的个数）。
对每个居民区，统计被该组合中多少个信号塔覆盖（通过mask & 居民区掩码的二进制 1 的个数）。
计算该组合的总价值（居民区价值 // 覆盖次数，覆盖次数为 0 则贡献 0）。

（3）筛选最优解

遍历所有组合后，找到总价值最大 的组合；若有多个组合价值相同，选择激活数量最少的。

java 复制代码

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

class Tower {
    int x, y;//坐标
    int r;//半径

    public Tower(int x, int y, int r) {
        this.x = x;
        this.y = y;
        this.r = r;
    }
}

class House {
    int x, y;//坐标
    int value;//价值
    int mask;//利用bit位标识被哪些塔覆盖了

    public House(int x, int y, int value, int mask) {
        this.x = x;
        this.y = y;
        this.value = value;
        this.mask = mask;
    }
}

public class Main {
    private static List<Tower> towerList;
    private static List<House> houseList;
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        towerList = new ArrayList<>();//存储塔
        houseList = new ArrayList<>();//存储居民楼
        //1.初始化建立图，并存储所有的信号塔内容，居民楼内容
        int m = scanner.nextInt();
        int n = scanner.nextInt();
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                int value = scanner.nextInt();
                if (value < 0) {
                    towerList.add(new Tower(i, j, value));
                } else if (value > 0) {
                    houseList.add(new House(i, j, value, 0));
                }
            }
        }
        scanner.close();
        //2.根据信号塔的覆盖情况设置居民楼的覆盖掩码
        for (House house : houseList) {
            for (int i = 0; i < towerList.size(); i++) {
                Tower tower = towerList.get(i);
                //2.1计算编号为i的塔到居民楼的欧几里得距离
                double dist = Math.pow(house.x - tower.x, 2) + Math.pow(house.y - tower.y, 2);
                //2.2如果能覆盖则更新居民楼的覆盖掩码，第i位bit位置1
                if (dist <= Math.pow(tower.r, 2)) {
                    house.mask |= (1 << i);
                }
            }
        }
        //3.利用bit位标识哪些编号的塔激活，枚举找到达到最大价值时最少的激活塔数量
        int maxValue = Integer.MIN_VALUE;
        int activitedCount = Integer.MAX_VALUE;
        for (int mask = 0; mask < (1 << towerList.size()); mask++) {
            int curMaxVal = 0;
            int curActCount = Integer.bitCount(mask);
            //3.1累加每个被覆盖的居民楼价值
            for (House house : houseList) {
                int cover = Integer.bitCount(house.mask & mask);
                if (cover > 0) {
                    curMaxVal += house.value / cover;
                }
            }
            //3.2更新结果
            if (maxValue < curMaxVal) {
                maxValue = curMaxVal;
                activitedCount = curActCount;
            } else if (maxValue == curMaxVal) {
                activitedCount = Math.min(activitedCount, curActCount);
            }
        }
        //4.输出结果
        System.out.println(maxValue + " " + activitedCount);
    }
}