目录
[6.3. 填充和步幅](#6.3. 填充和步幅)
[6.3.1. 填充](#6.3.1. 填充)
[6.3.2. 步幅](#6.3.2. 步幅)
[6.4. 多输入多输出通道](#6.4. 多输入多输出通道)
[6.4.1. 多输入通道](#6.4.1. 多输入通道)
[6.4.2. 多输出通道](#6.4.2. 多输出通道)
[6.4.3. 1*1卷积层](#6.4.3. 1*1卷积层)
6.3. 填充和步幅
在6.2节时,我们把输入经过卷积之后发现,输出小于输入。那么有什么办法,让输出和输入大小相等呢?
再问一个更一般的问题,除了输入大小和卷积核的大小,还有什么影响输出大小?
这就是我们这节要介绍的填充和步幅。
6.3.1. 填充
我们直接看图:
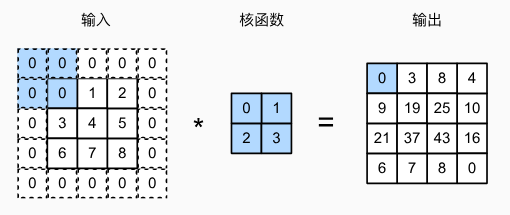
在原本的输入外,添加一圈0,这就是填充。
当然,不一定添加一圈,添加的数字也不一定就是0,根据具体情况,我们可以灵活设置参数的。现在我们只要知道填充是个什么东西就行了。
我们刚才说了,输出大小也受ph行填充,pw列填充影响,输出大小为:
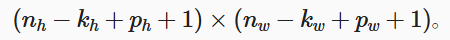
这意味着输出的高度和宽度将分别增加ph和pw。
让输入和输出大小相等
相等的意义:因为可以在构建网络时更容易地预测每个图层的输出形状。
怎么做:让ph = kh - 1, pw = kw - 1
如果kh和kw是偶数,填充的话就无法平均分到行上下两侧,列左右两侧。这个时候我们需要在上方和左边多加一个。也就是[ph,pw]/2,向上取整。
既然偶数这么麻烦,所以我们干脆让卷积核的kh和kw取奇数。
这样还有一个好处。
当满足: 1. 卷积核的大小是奇数; 2. 所有边的填充行数和列数相同; 3. 输出与输入具有相同高度和宽度 则可以得出:
输出Y[i, j]是通过以输入X[i, j]为中心,与卷积核进行互相关计算得到的。
接下来我们看代码:
python
import torch
from torch import nn
# 为了方便起见,我们定义了一个计算卷积层的函数。
# 此函数初始化卷积层权重,并对输入和输出提高和缩减相应的维数
def comp_conv2d(conv2d, X):
# 这里的(1,1)表示批量大小和通道数都是1
X = X.reshape((1, 1) + X.shape)
Y = conv2d(X)
return Y.reshape(Y.shape[2:]) # 省略前两个维度:批量大小和通道
# 请注意,这里每边都填充了1行或1列,因此总共添加了2行或2列
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)
X = torch.rand(size=(8, 8))
print(comp_conv2d(conv2d, X).shape)上面创建一个高度和宽度为3的二维卷积层,并在所有侧边填充1个像素。给定高度和宽度为8的输入,则输出的高度和宽度也是8。
运行结果:
torch.Size([8, 8])
6.3.2. 步幅
在进行互相关计算的时候,卷积核开始沿着如何自左向右,自上而下滑动。并且每次滑动默认都是一个元素。
而步幅就是控制一次滑动几个元素的超参数。
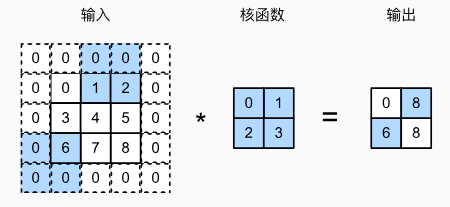
步幅是如何改变输出大小的?
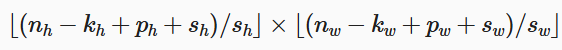
最外层括号是向下取整。
输出大小根据上面的式子得出,其中sh和sw分别是水平步幅和垂直步幅。
让ph = kh - 1, pw = kw - 1,我们可以得到以下简化的式子:
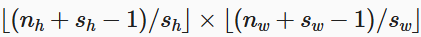
如果输入的高度和宽度可以被垂直和水平步幅整除,则可以进一步简化:

这一点很好理解,加入输入是4*4,步幅为2。
则4+2-1 = 5,让5/2向下取整 = 4/2。
python
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)
comp_conv2d(conv2d, X).shape运行结果:torch.Size([4, 4])
以下是一个更为一般的例子:
python
conv2d = nn.Conv2d(1, 1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))
comp_conv2d(conv2d, X).shape我们不妨手动计算一下:
(8 - 3 + 0 + 3)/ 3 = 2
(8 - 5 + 1 + 4)/ 4 = 2
运行结果:torch.Size([2, 2]),可以看到和我们计算的一样。
默认情况下,填充为0,步幅为1。在实践中,我们很少使用不一致的步幅或填充,也就是ph = pw,sh = sw
6.4. 多输入多输出通道
上一节,我们仅展示了单个输入和单个输出通道。这使得我们可以将输入、卷积核和输出看作二维张量。
这一节,我们添加通道时,我们的输入和隐藏的表示都变成了三维张量。除了之前的h(高)、w(宽),我们增加了channel(通道)维度。
6.4.1. 多输入通道
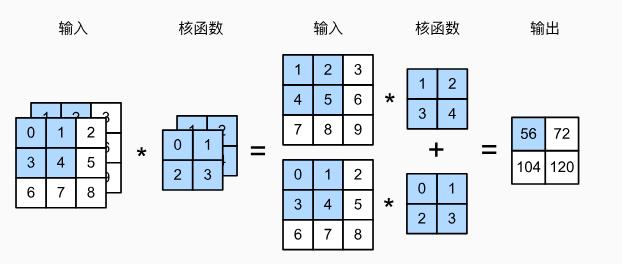
可以看到,这张图十分的清晰的说明了多输入通道。
相比于我们之前的单个二维张量,我们这边多加了个channel。
计算输出也很简单,分别计算之后相加就行。
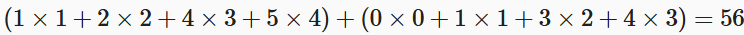
知道原理之后,我们来手搓一下。
python
import torch
from d2l import torch as d2l
def corr2d_multi_in(X, K):
# 先遍历"X"和"K"的第0个维度(通道维度),再把它们加在一起
return sum(d2l.corr2d(x, k) for x, k in zip(X, K))我们来解释一下这段代码:
zip(X, K) 的作用:
假设:
X = [通道1数据, 通道2数据, 通道3数据] (3个通道)
K = [卷积核1, 卷积核2, 卷积核3] (3个卷积核)
zip(X, K) 会产生:
(通道1数据, 卷积核1), (通道2数据, 卷积核2), (通道3数据, 卷积核3)
利用for循环遍历每个通道对,然后用sum()求和。
给个数据测试一下:
python
X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
[[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])
print(corr2d_multi_in(X, K))运行结果:
tensor([[ 56., 72.],
104., 120.\]\]) ### 6.4.2. 多输出通道 到目前为止,不论有多少输入通道,我们还只有一个输出通道。然而,每一层有多个输出通道是至关重要的。在最流行的神经网络架构中,随着神经网络层数的加深,我们常会增加输出通道的维数,通过减少空间分辨率以获得更大的通道深度。 以上的不重要,目前只要记住,多输出通道有一定的现实意义。 ```python def corr2d_multi_in_out(X, K): # 迭代"K"的第0个维度,每次都对输入"X"执行互相关运算。 # 最后将所有结果都叠加在一起 return torch.stack([corr2d_multi_in(X, k) for k in K], 0) ``` **参数说明** **X** : 输入张量,形状为 `[输入通道数, 高度, 宽度]` **K** : 卷积核张量,形状为 `[输出通道数, 输入通道数, 卷积核高度, 卷积核宽度]` **返回值** : 多通道输出特征图,形状为 `[输出通道数, 输出高度, 输出宽度]` for k in K#根据K的输出通道,遍历K中的k,然后进行多输入卷积。 把结果交给torch.stack组织。 torch.stack会创建批次维度,合并多个输出通道,组织时间序列数据。 我们给数据测试下: 通过将核张量`K`与`K+1`(`K`中每个元素加1)和`K+2`连接起来,构造了一个具有个3输出通道的卷积核。 ```python K = torch.stack((K, K + 1, K + 2), 0) print(K.shape) print(corr2d_multi_in_out(X, K)) ``` 输出结果: torch.Size(\[3, 2, 2, 2\]) tensor(\[\[\[ 56., 72.\], \[104., 120.\]\], \[\[ 76., 100.\], \[148., 172.\]\], \[\[ 96., 128.\], \[192., 224.\]\]\]) ### 6.4.3. 1\*1卷积层 1x1卷积层是一种特殊的卷积层,它使用1x1的卷积核。尽管它不能捕捉空间模式(因为卷积核大小是1x1),但它可以融合多个通道的信息。经常被用来控制模型的复杂度和减少计算量。 1x1卷积层的作用: · **调整通道数**:通过使用不同数量的1x1卷积核,我们可以增加或减少输出通道数。 **增加非线性**:在1x1卷积后通常使用激活函数,从而引入非线性。 **跨通道的信息交互**:1x1卷积可以看作是对每个像素点,在不同通道上的线性组合。 ```python def corr2d_multi_in_out_1x1(X, K): # 获取输入形状 c_i, h, w = X.shape # 输入通道数, 高度, 宽度 # 获取输出通道数 c_o = K.shape[0] # 输出通道数 # 重塑输入: 将空间维度展平 X = X.reshape((c_i, h * w)) # 形状从 [c_i, h, w] → [c_i, h*w] # 重塑卷积核: 展平通道维度 K = K.reshape((c_o, c_i)) # 形状从 [c_o, c_i, 1, 1] → [c_o, c_i] # 矩阵乘法实现全连接 Y = torch.matmul(K, X) # 形状: [c_o, c_i] × [c_i, h*w] = [c_o, h*w] # 恢复空间维度 return Y.reshape((c_o, h, w)) # 形状: [c_o, h*w] → [c_o, h, w] #当执行1*1卷积运算时,上述函数相当于先前实现的互相关函数corr2d_multi_in_out。 Y1 = corr2d_multi_in_out_1x1(X, K) Y2 = corr2d_multi_in_out(X, K) assert float(torch.abs(Y1 - Y2).sum()) < 1e-6#检测是不是二者是不是一样 print(Y1) print(Y2) ``` 运行结果: tensor(\[\[\[ 2.5441, -0.5992, -1.6702\], \[ 0.8812, 1.5099, -0.3698\], \[ 3.0920, 2.5063, 1.5707\]\], \[\[ 1.8365, -2.3701, -1.3319\], \[-0.6865, 1.4876, -0.2101\], \[ 2.1789, 1.9134, -1.0353\]\]\]) tensor(\[\[\[ 2.5441, -0.5992, -1.6702\], \[ 0.8812, 1.5099, -0.3698\], \[ 3.0920, 2.5063, 1.5707\]\],