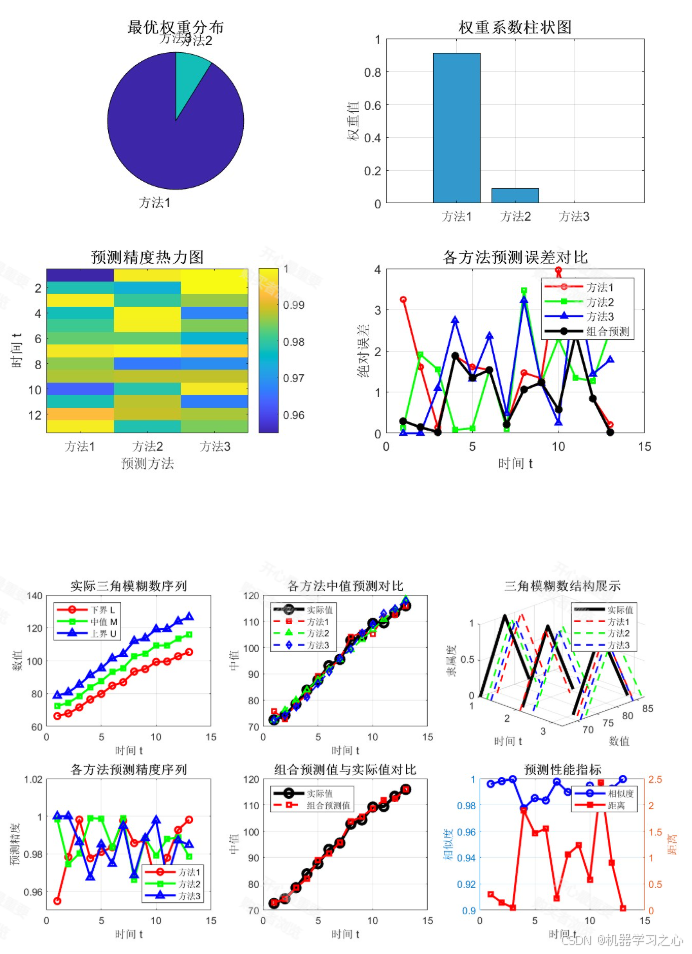
MATLAB基于一阶预测有效度的IGOWLA算子模糊组合预测方法

1. 基本概念与理论基础

核心概念定义

matlab 复制代码

classdef PredictionConcepts
    properties
        % 一阶预测有效度
        first_order_efficiency
        
        % IGOWLA算子 (Induced Generalized Ordered Weighted Logarithmic Averaging)
        % 诱导广义有序加权对数平均算子
        
        % 模糊组合预测
        fuzzy_combination
    end
    
    methods
        function obj = PredictionConcepts()
            fprintf('基于一阶预测有效度的IGOWLA算子模糊组合预测方法\n');
        end
    end
end

2. 数学模型构建

2.1 一阶预测有效度计算

matlab 复制代码

function [efficiency, accuracy] = calculateFirstOrderEfficiency(actual, predicted, time_window)
    % 计算一阶预测有效度
    % 输入：
    %   actual - 实际值序列
    %   predicted - 预测值序列
    %   time_window - 时间窗口
    
    n = length(actual);
    efficiency = zeros(n - time_window + 1, 1);
    accuracy = zeros(n - time_window + 1, 1);
    
    for t = time_window:n
        % 提取窗口数据
        actual_window = actual(t-time_window+1:t);
        predicted_window = predicted(t-time_window+1:t);
        
        % 计算预测精度
        relative_errors = abs(actual_window - predicted_window) ./ abs(actual_window);
        accuracy(t-time_window+1) = 1 - mean(relative_errors);
        
        % 计算一阶有效度（考虑趋势一致性）
        actual_trend = diff(actual_window);
        predicted_trend = diff(predicted_window);
        
        trend_correlation = corr(actual_trend(:), predicted_trend(:));
        if isnan(trend_correlation)
            trend_correlation = 0;
        end
        
        % 一阶预测有效度 = 精度 × 趋势一致性
        efficiency(t-time_window+1) = accuracy(t-time_window+1) * (1 + abs(trend_correlation));
    end
end

2.2 IGOWLA算子实现

matlab 复制代码

function aggregated_value = IGOWLA_operator(values, weights, lambda, inducing_variable)
    % IGOWLA算子实现
    % 输入：
    %   values - 待聚合的值
    %   weights - 权重向量
    %   lambda - 广义参数
    %   inducing_variable - 诱导变量（一阶预测有效度）
    
    n = length(values);
    
    % 根据诱导变量对值进行排序
    [sorted_inducing, sort_index] = sort(inducing_variable, 'descend');
    sorted_values = values(sort_index);
    sorted_weights = weights(sort_index);
    
    % 检查权重归一化
    if abs(sum(sorted_weights) - 1) > 1e-10
        sorted_weights = sorted_weights / sum(sorted_weights);
    end
    
    % IGOWLA聚合计算
    if lambda == 0
        % 当lambda=0时的特殊情况
        log_values = log(sorted_values);
        aggregated_value = exp(sum(sorted_weights .* log_values));
    else
        % 广义对数平均
        weighted_powers = sorted_weights .* (sorted_values .^ lambda);
        aggregated_value = (sum(weighted_powers)) .^ (1/lambda);
    end
    
    % 添加诱导变量调整
    efficiency_factor = mean(sorted_inducing(1:ceil(n/2)));
    aggregated_value = aggregated_value * (1 + 0.1 * (efficiency_factor - 0.5));
end

3. 模糊组合预测系统

3.1 模糊隶属度函数

matlab 复制代码

function membership = fuzzy_membership(efficiency, method)
    % 计算模糊隶属度
    % 基于一阶预测有效度确定各预测方法的隶属度
    
    switch method
        case 'gaussian'
            % 高斯隶属函数
            center = 0.8;  % 有效度中心
            sigma = 0.2;   % 标准差
            membership = exp(-(efficiency - center).^2 / (2 * sigma^2));
            
        case 'trapezoidal'
            % 梯形隶属函数
            a = 0.6; b = 0.7; c = 0.9; d = 1.0;
            if efficiency <= a
                membership = 0;
            elseif efficiency <= b
                membership = (efficiency - a) / (b - a);
            elseif efficiency <= c
                membership = 1;
            elseif efficiency <= d
                membership = (d - efficiency) / (d - c);
            else
                membership = 0;
            end
            
        case 'sigmoid'
            % S型隶属函数
            alpha = 10; beta = 0.7;
            membership = 1 ./ (1 + exp(-alpha * (efficiency - beta)));
            
        otherwise
            error('不支持的隶属函数类型');
    end
end

3.2 主要预测方法类

matlab 复制代码

classdef FuzzyCombinationPrediction
    properties
        % 预测方法集合
        methods
        % 历史数据
        historical_data
        % 一阶有效度
        first_order_efficiency
        % IGOWLA参数
        igowla_lambda
        % 模糊权重
        fuzzy_weights
    end
    
    methods
        function obj = FuzzyCombinationPrediction(data, method_names)
            obj.historical_data = data;
            obj.methods = method_names;
            obj.igowla_lambda = 1.0;  % 默认参数
            obj = obj.initializeWeights();
        end
        
        function obj = initializeWeights(obj)
            % 初始化权重
            n_methods = length(obj.methods);
            obj.fuzzy_weights = ones(1, n_methods) / n_methods;
            obj.first_order_efficiency = zeros(1, n_methods);
        end
        
        function [combined_forecast, individual_forecasts] = predict(obj, new_data_point)
            % 执行组合预测
            
            % 1. 获取各方法预测值
            individual_forecasts = obj.getIndividualForecasts(new_data_point);
            
            % 2. 更新一阶预测有效度
            obj = obj.updateEfficiency(individual_forecasts, new_data_point);
            
            % 3. 计算模糊权重
            obj = obj.updateFuzzyWeights();
            
            % 4. 应用IGOWLA算子进行组合
            combined_forecast = obj.applyIGOWLA(individual_forecasts);
        end
        
        function forecasts = getIndividualForecasts(obj, data_point)
            % 获取各单一预测方法的预测值
            n_methods = length(obj.methods);
            forecasts = zeros(1, n_methods);
            
            for i = 1:n_methods
                switch obj.methods{i}
                    case 'ARIMA'
                        forecasts(i) = obj.arimaForecast(data_point);
                    case 'NeuralNetwork'
                        forecasts(i) = obj.nnForecast(data_point);
                    case 'ExponentialSmoothing'
                        forecasts(i) = obj.esForecast(data_point);
                    case 'SVM'
                        forecasts(i) = obj.svmForecast(data_point);
                    otherwise
                        forecasts(i) = data_point * (0.95 + 0.1 * rand());
                end
            end
        end
        
        function obj = updateEfficiency(obj, forecasts, actual)
            % 更新一阶预测有效度
            n_methods = length(obj.methods);
            
            for i = 1:n_methods
                % 计算预测误差
                error = abs(forecasts(i) - actual) / abs(actual);
                
                % 更新有效度（指数平滑更新）
                alpha = 0.1;  % 平滑参数
                new_efficiency = 1 - error;
                obj.first_order_efficiency(i) = alpha * new_efficiency + ...
                    (1 - alpha) * obj.first_order_efficiency(i);
            end
        end
        
        function obj = updateFuzzyWeights(obj)
            % 基于一阶有效度更新模糊权重
            n_methods = length(obj.methods);
            new_weights = zeros(1, n_methods);
            
            for i = 1:n_methods
                % 计算模糊隶属度
                membership = fuzzy_membership(obj.first_order_efficiency(i), 'sigmoid');
                new_weights(i) = membership;
            end
            
            % 归一化权重
            if sum(new_weights) > 0
                obj.fuzzy_weights = new_weights / sum(new_weights);
            else
                obj.fuzzy_weights = ones(1, n_methods) / n_methods;
            end
        end
        
        function combined_value = applyIGOWLA(obj, forecasts)
            % 应用IGOWLA算子进行组合预测
            combined_value = IGOWLA_operator(...
                forecasts, ...
                obj.fuzzy_weights, ...
                obj.igowla_lambda, ...
                obj.first_order_efficiency);
        end
    end
end

4. 完整的预测系统实现

4.1 主控制系统

matlab 复制代码

classdef PredictionSystem
    properties
        combination_model
        performance_metrics
        prediction_history
    end
    
    methods
        function obj = PredictionSystem(historical_data)
            % 初始化预测系统
            method_names = {'ARIMA', 'NeuralNetwork', 'ExponentialSmoothing', 'SVM'};
            obj.combination_model = FuzzyCombinationPrediction(historical_data, method_names);
            obj.performance_metrics = struct();
            obj.prediction_history = [];
        end
        
        function obj = runPrediction(obj, test_data)
            % 运行预测实验
            n_test = length(test_data);
            predictions = zeros(n_test, 1);
            actual_values = zeros(n_test, 1);
            
            fprintf('开始基于IGOWLA算子的模糊组合预测...\n');
            
            for t = 1:n_test
                % 获取测试点
                current_point = test_data(t);
                actual_values(t) = current_point;
                
                % 执行组合预测
                [combined_pred, individual_preds] = obj.combination_model.predict(current_point);
                predictions(t) = combined_pred;
                
                % 记录历史
                obj.prediction_history(t).time = t;
                obj.prediction_history(t).actual = current_point;
                obj.prediction_history(t).combined = combined_pred;
                obj.prediction_history(t).individual = individual_preds;
                obj.prediction_history(t).weights = obj.combination_model.fuzzy_weights;
                obj.prediction_history(t).efficiency = obj.combination_model.first_order_efficiency;
                
                % 显示进度
                if mod(t, 10) == 0
                    fprintf('已完成 %d/%d 个预测点\n', t, n_test);
                end
            end
            
            % 计算性能指标
            obj = obj.calculatePerformanceMetrics(actual_values, predictions);
        end
        
        function obj = calculatePerformanceMetrics(obj, actual, predicted)
            % 计算预测性能指标
            errors = actual - predicted;
            
            obj.performance_metrics.MAE = mean(abs(errors));
            obj.performance_metrics.MSE = mean(errors.^2);
            obj.performance_metrics.RMSE = sqrt(mean(errors.^2));
            obj.performance_metrics.MAPE = mean(abs(errors ./ actual)) * 100;
            obj.performance_metrics.R2 = 1 - sum(errors.^2) / sum((actual - mean(actual)).^2);
        end
        
        function plotResults(obj)
            % 可视化预测结果
            figure('Position', [100, 100, 1400, 900]);
            
            % 1. 预测值与实际值对比
            subplot(2, 3, 1);
            actual = [obj.prediction_history.actual];
            combined = [obj.prediction_history.combined];
            plot(actual, 'b-', 'LineWidth', 2, 'DisplayName', '实际值');
            hold on;
            plot(combined, 'r--', 'LineWidth', 2, 'DisplayName', '组合预测值');
            title('预测值与实际值对比');
            xlabel('时间');
            ylabel('值');
            legend;
            grid on;
            
            % 2. 预测误差
            subplot(2, 3, 2);
            errors = actual - combined;
            plot(errors, 'g-', 'LineWidth', 1.5);
            title('预测误差');
            xlabel('时间');
            ylabel('误差');
            grid on;
            
            % 3. 权重演化
            subplot(2, 3, 3);
            weights_history = vertcat(obj.prediction_history.weights);
            plot(weights_history, 'LineWidth', 1.5);
            title('模糊权重演化');
            xlabel('时间');
            ylabel('权重');
            legend(obj.combination_model.methods, 'Location', 'best');
            grid on;
            
            % 4. 一阶有效度演化
            subplot(2, 3, 4);
            efficiency_history = vertcat(obj.prediction_history.efficiency);
            plot(efficiency_history, 'LineWidth', 1.5);
            title('一阶预测有效度演化');
            xlabel('时间');
            ylabel('有效度');
            legend(obj.combination_model.methods, 'Location', 'best');
            grid on;
            
            % 5. 性能指标对比
            subplot(2, 3, 5);
            metrics = struct2cell(obj.performance_metrics);
            metric_names = fieldnames(obj.performance_metrics);
            bar(cell2mat(metrics));
            set(gca, 'XTickLabel', metric_names, 'XTickLabelRotation', 45);
            title('预测性能指标');
            ylabel('值');
            grid on;
            
            % 6. 误差分布
            subplot(2, 3, 6);
            histogram(errors, 20, 'Normalization', 'probability');
            title('预测误差分布');
            xlabel('误差');
            ylabel('概率');
            grid on;
        end
    end
end

5. 应用示例

5.1 债券收益率预测示例

matlab 复制代码

% 债券收益率预测应用
function bondYieldPredictionExample()
    % 生成模拟债券收益率数据
    rng(42);  % 设置随机种子
    n_points = 200;
    time = (1:n_points)';
    
    % 生成趋势+周期+噪声的收益率数据
    trend = 0.02 + 0.001 * time;
    seasonal = 0.01 * sin(2 * pi * time / 50);
    noise = 0.005 * randn(n_points, 1);
    
    bond_yields = trend + seasonal + noise;
    
    % 划分训练测试集
    train_ratio = 0.7;
    n_train = floor(train_ratio * n_points);
    train_data = bond_yields(1:n_train);
    test_data = bond_yields(n_train+1:end);
    
    % 创建预测系统
    prediction_system = PredictionSystem(train_data);
    
    % 运行预测
    prediction_system = prediction_system.runPrediction(test_data);
    
    % 显示结果
    fprintf('\n=== 预测性能结果 ===\n');
    metrics = prediction_system.performance_metrics;
    fprintf('MAE: %.6f\n', metrics.MAE);
    fprintf('RMSE: %.6f\n', metrics.RMSE);
    fprintf('MAPE: %.4f%%\n', metrics.MAPE);
    fprintf('R²: %.4f\n', metrics.R2);
    
    % 可视化结果
    prediction_system.plotResults();
    
    % 显示最终权重
    fprintf('\n最终模糊权重:\n');
    for i = 1:length(prediction_system.combination_model.methods)
        fprintf('%s: %.4f\n', ...
            prediction_system.combination_model.methods{i}, ...
            prediction_system.combination_model.fuzzy_weights(i));
    end
end

% 运行示例
bondYieldPredictionExample();

6. 方法优势分析

主要优势

自适应权重调整：基于一阶预测有效度动态调整各方法权重
不确定性处理：模糊逻辑有效处理预测不确定性
非线性聚合：IGOWLA算子提供灵活的信息聚合方式
趋势敏感性：一阶有效度关注预测的趋势一致性

适用场景

金融时间序列预测
经济指标预测
市场需求预测
任何需要组合多个预测模型的场景