从三路快排到内省排序：探索工业级排序算法的演进

前言

大家好啊，我是云泽Q，欢迎阅读我的文章，一名热爱计算机技术的在校大学生，喜欢在课余时间做一些计算机技术的总结性文章，希望我的文章能为你解答困惑~

一、快速排序性能的关键点分析

决定快排性能的关键点是每次单趟排序后，key对数组的分割，如果每次选key基本二分居中，那么快排的递归树就是棵均匀的满二叉树，性能最佳。但是实践中虽然不可能每次都是二分居中，但是性能也还是可控的。但是如果出现每次选到最小值/最大值，且数组中有大量重复的数据时，划分为0个和N-1的子问题时，时间复杂度为O（N²）

c 复制代码

//数组中有多个跟key相等的值
int a[] = { 6,1,7,6,6,6,4,9 };
int a[] = { 3,2,3,3,3,3,2,3 };
//数组中全是相同的值
int a[] = { 2,2,2,2,2,2,2,2 };

下面就提供一种叫三路划分的解决方案

1.1 三路划分算法思想解析

当面对有大量跟key相同的值时，三路划分的核心思想有点类似hoare的左右指针和lomuto的前后指针的结合。核心思想是把数组中的数据分为三段[比key小的值]，[跟key相等的值]，[比key大的值]，所以叫做三路划分算法。结合下图，理解一下实现思想：

key默认取left位置的值，left指向区间最左边，right指向区间最右边，cur指向left+1位置

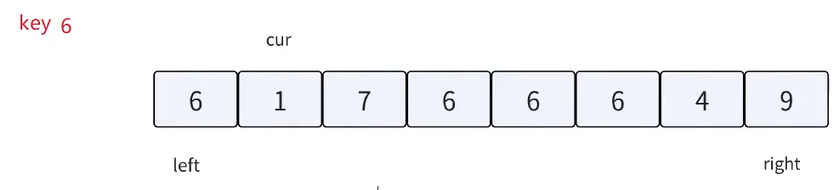
cur从左向右走，遇到比key小的值后跟left位置交换，换到左边，left++，cur++

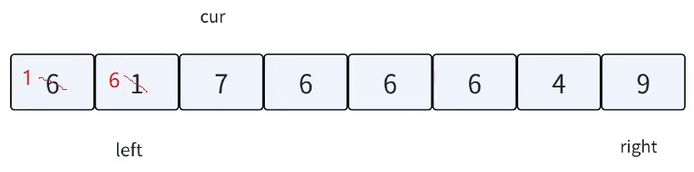
可以看到此时left依旧指向key，cur遇到比key大的值跟right位置交换，换到右边，right减减

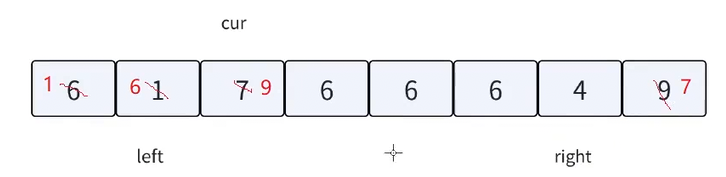
此时cur遇到的值（9）比key大，和right交换，换到右边，right减减

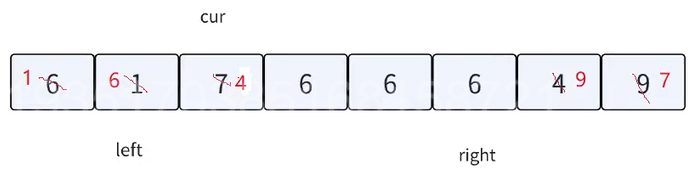
此时cur遇到的值比key小，跟left交换，换到左边，left++，cur减减

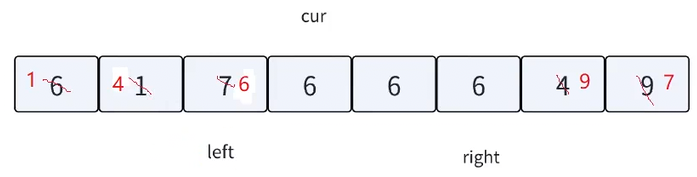
此时cur遇到和key相等的值，cur++，直到cur>right结束

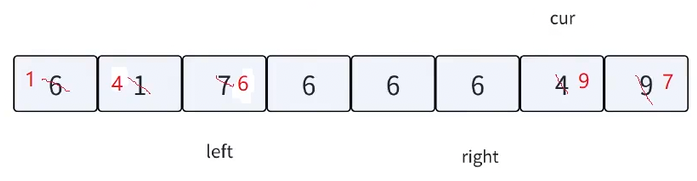
//开始递归，中间和key相等的值不用动

1.2 三路快排单趟排序运行结果分析

排序数组，下面通过这个OJ题来展示一下三路划分快排在该场景下的表现，在这个OJ中，用快排的lomuto的方法时是过不了题目的（lomuto的前后指针面对大量数据重复时，效率会退化），hoare版本可以过这个题目，堆排序和归并和希尔是可以过的，其他几个O（N²）也过不了，因为这个题的测试用例中不仅仅有数据很多的大数组，也有一些特殊数据的数组。堆排序和归并和希尔不是很受数据样本的分布和形态的影响，但是快排会，因为快排要选key，每次key都当趟分隔都很偏，就会出现效率退化问题。

补充一下，三路划分虽然在针对有大量重复数据时效率很好，但也并不是完美的，如果三路划分单趟选基准值的时候，就是运气很差，每次划分选到的就是最小/次小的值作为key，那还是会有一些性能退化。没有一个排序算法是完美无瑕能同时兼备高效和稳定的，在一方面的效果很好情况下，必定是要在其他方面付出一些代价的，三路划分的排序思想在特殊场景下效率也会退化，所以算法的场景要结合具体的场景和需求。冒泡排序和直接插入排序除外除外，我个人觉得这两个排序算法除了有一些教学价值基本0作用

二、内省排序（优秀的工业级排序）

introsort是由David Musser在1997年设计的排序算法，C++sgi STL sort中就是用的introspective sort（内省排序）思想实现的。内省排序可以认为不受数据分布的影响，无论什么原因划分不均匀，导致递归深度太深，他就是转换堆排序了，堆排不受数据分布影响。

introsort是introspective sort采用了缩写，他的名字其实表达了他的实现思路，他的思路就是进行自我侦测和反省，快排递归深度太深(sgi STL中使用的是深度为2倍排序元素数量的对数值)那就说明在这种数据序列下，选key出现了问题，性能在快速退化，那么就不要再进行快排分割递归了，改换为堆排序进行排序。

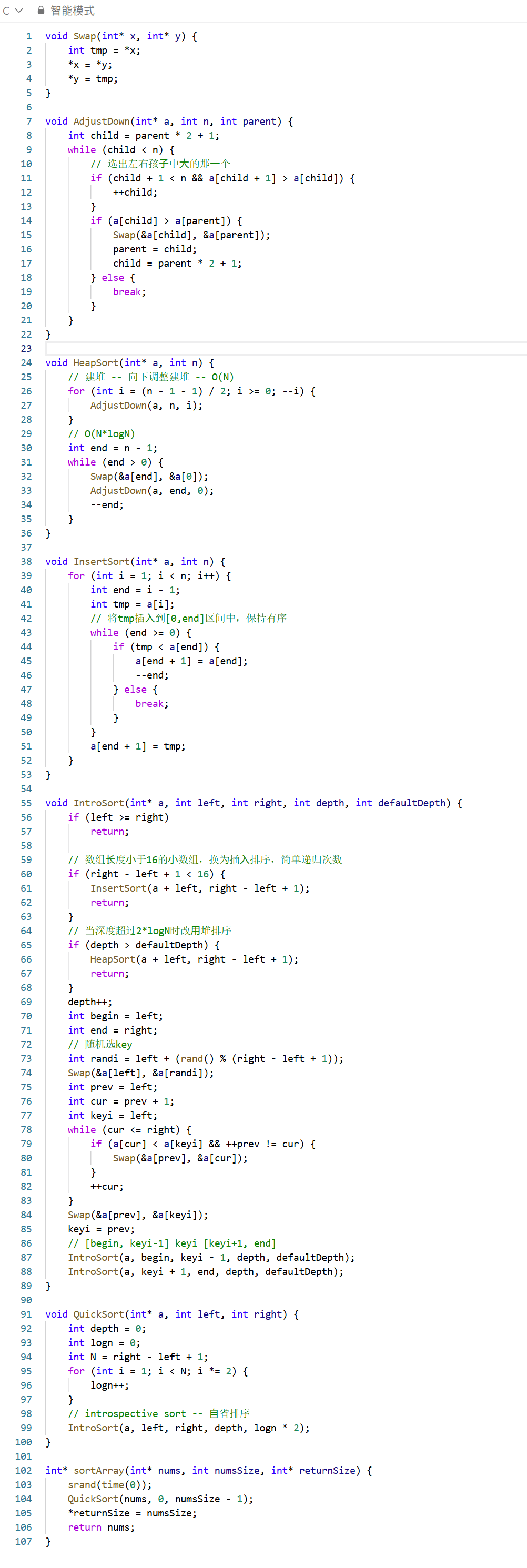
这里计算深度是定义了一个参数值，每向下递归一层，这个形参就++

三、力扣源码

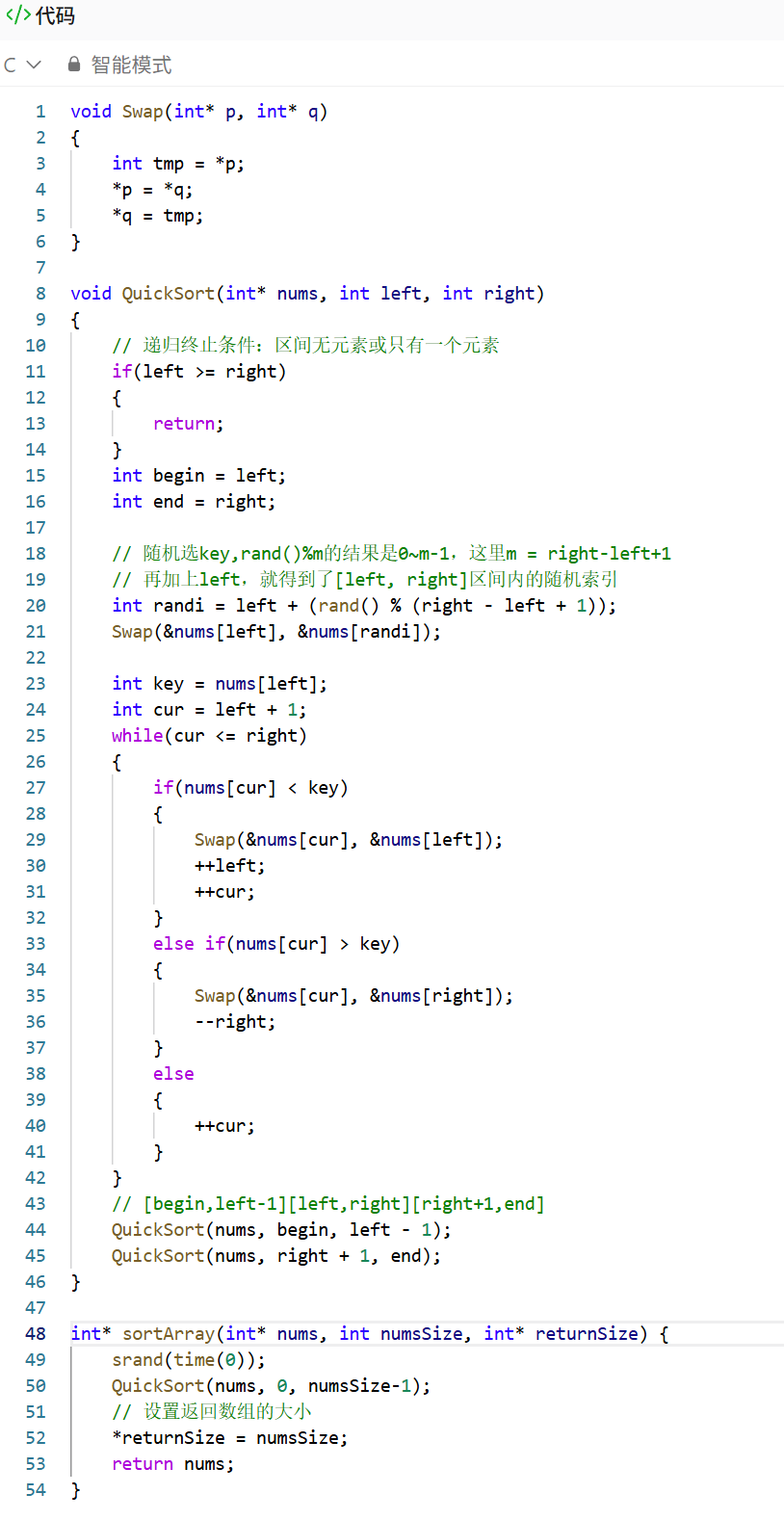
快排三路划分

c 复制代码

void Swap(int* p, int* q)
{
    int tmp = *p;
    *p = *q;
    *q = tmp;
}

void QuickSort(int* nums, int left, int right)
{
    if(left >= right)
    {
        return;
    }
    int begin = left;
    int end = right;

    int randi = left + (rand() % (right - left + 1));
    Swap(&nums[left], &nums[randi]);

    int key = nums[left];
    int cur = left + 1;
    while(cur <= right)
    {
        if(nums[cur] < key)
        {
            Swap(&nums[cur], &nums[left]);
            ++left;
            ++cur;
        }
        else if(nums[cur] > key)
        {
            Swap(&nums[cur], &nums[right]);
            --right;
        }
        else
        {
            ++cur;
        }
    }
    QuickSort(nums, begin, left - 1);
    QuickSort(nums, right + 1, end);
}

int* sortArray(int* nums, int numsSize, int* returnSize) {
    srand(time(0));
    QuickSort(nums, 0, numsSize-1);
    *returnSize = numsSize;
    return nums;
}

自省排序

c 复制代码

void Swap(int* x, int* y) {
    int tmp = *x;
    *x = *y;
    *y = tmp;
}

void AdjustDown(int* a, int n, int parent) {
    int child = parent * 2 + 1;
    while (child < n) {
        // 选出左右孩⼦中⼤的那⼀个
        if (child + 1 < n && a[child + 1] > a[child]) {
            ++child;
        }
        if (a[child] > a[parent]) {
            Swap(&a[child], &a[parent]);
            parent = child;
            child = parent * 2 + 1;
        } else {
            break;
        }
    }
}

void HeapSort(int* a, int n) {
    // 建堆 -- 向下调整建堆 -- O(N)
    for (int i = (n - 1 - 1) / 2; i >= 0; --i) {
        AdjustDown(a, n, i);
    }
    // O(N*logN)
    int end = n - 1;
    while (end > 0) {
        Swap(&a[end], &a[0]);
        AdjustDown(a, end, 0);
        --end;
    }
}

void InsertSort(int* a, int n) {
    for (int i = 1; i < n; i++) {
        int end = i - 1;
        int tmp = a[i];
        // 将tmp插⼊到[0,end]区间中，保持有序
        while (end >= 0) {
            if (tmp < a[end]) {
                a[end + 1] = a[end];
                --end;
            } else {
                break;
            }
        }
        a[end + 1] = tmp;
    }
}

void IntroSort(int* a, int left, int right, int depth, int defaultDepth) {
    if (left >= right)
        return;

    // 数组⻓度⼩于16的⼩数组，换为插⼊排序，简单递归次数
    if (right - left + 1 < 16) {
        InsertSort(a + left, right - left + 1);
        return;
    }
    // 当深度超过2*logN时改⽤堆排序
    if (depth > defaultDepth) {
        HeapSort(a + left, right - left + 1);
        return;
    }
    depth++;
    int begin = left;
    int end = right;
    // 随机选key 
    int randi = left + (rand() % (right - left + 1));
    Swap(&a[left], &a[randi]);
    int prev = left;
    int cur = prev + 1;
    int keyi = left;
    while (cur <= right) {
        if (a[cur] < a[keyi] && ++prev != cur) {
            Swap(&a[prev], &a[cur]);
        }
        ++cur;
    }
    Swap(&a[prev], &a[keyi]);
    keyi = prev;
    // [begin, keyi-1] keyi [keyi+1, end]
    IntroSort(a, begin, keyi - 1, depth, defaultDepth);
    IntroSort(a, keyi + 1, end, depth, defaultDepth);
}

void QuickSort(int* a, int left, int right) {
    int depth = 0;
    int logn = 0;
    int N = right - left + 1;
    for (int i = 1; i < N; i *= 2) {
        logn++;
    }
    // introspective sort -- ⾃省排序
    IntroSort(a, left, right, depth, logn * 2);
}

int* sortArray(int* nums, int numsSize, int* returnSize) {
    srand(time(0));
    QuickSort(nums, 0, numsSize - 1);
    *returnSize = numsSize;
    return nums;
}

从三路快排到内省排序：探索工业级排序算法的演进

目录

前言

一、快速排序性能的关键点分析

1.1 三路划分算法思想解析

1.2 三路快排单趟排序运行结果分析

二、内省排序（优秀的工业级排序）

三、力扣源码

结语