PyTorch:基于python语言的深度学习框架,将数据封装为张量
下载包:pip istall 报名 -i 镜像
特点:
1.类似于numpyd 的张量计算
2.自动微分模块
3.深度学习库
4.动态学习库
5.GPU加速
6.支持多种应用场景
7.支持跨平台
张量的创建:张量:元素为同一数据类型的多维矩阵
0维:标量 1维:向量/矢量 2维:矩阵 3维:矩阵数组(2维张量的堆叠)
3,h, w: 3:通道数 h:高度 w:宽度
【3,4,5】三个四行五列的数组的堆叠
API:
torch.tensor:根据指定形状创建张量
torch.Tensor:根据形状创建张量(未初始化),其也可以用来创建指定数据类型的张量
torch.IntTensor torch.FloatTensor torch.DounbleTensor 创建指定类型的张量
import torch
import numpy as np
# 数据类型创建张量【标量,list,numpy】
def f01():
out=torch.tensor(5,)
print(type(out))
out2=torch.tensor([4,3,2])
print(type(out2))
out3=torch.tensor(np.array([1,2,3]))
print(type(out3))
# 根据数据形状来创建没有初始化
def f02():
# 通过指定维度大小创建张量
out=torch.Tensor(2,3)
print(out,out.shape,type(out),out.dtype)
# 将numpy数组转化为张量
out2 = torch.Tensor(np.array([5,6,7]))
print(out2, out2.shape, type(out2), out2.dtype)
# 创建指定类型的张量没有数值,所有只创建了形状
def f03():
# 创建整型
out=torch.IntTensor(2,3)
print(out,out.shape,type(out),out.dtype)
# 创建单精度浮点型
out2 = torch.FloatTensor(2,3)*0
print(out2, out2.shape, type(out2), out2.dtype)
# 创建双精度浮点型
out3 = torch.DoubleTensor(2,3)
print(out3, out3.shape, type(out3), out3.dtype)
if __name__ == '__main__':
# f01()
# f02()
f03()torch 运行时数据类型要求一致
线性张量和随机张量:
API:
torch.arange(1,10,2) 起始元素,终止元素,步长 包左不包右
torch.linspace(1,20,5) 起始元素,终止元素,几个元素 都包
torch.rand(300,500) 创建均匀分布的浮点型张量
torch.randn(300,500) 创建正态分布的浮点型张量
torch.initial_seed() 查看随机种子
torch.manual_seed(18) 固定随机种子
import torch
import matplotlib.pyplot as plt
# 线性张量,arange linspace
def f01():
out=torch.arange(1,10,2)
print(out,type(out),out.dtype)
out2=torch.linspace(1,20,5)
print(out2,type(out2),out2.dtype)
'''
随机张量
0-1之间的 rand
标准高斯正态分布 randn
randint 整型
initial_seed 返回随机数种子
manual_seed(v) 随机数种子的设置
'''
# rand
def f02():
out=torch.rand(300,500)
print(out,type(out),out.dtype)
# 将高维降到低维
out=out.flatten()
plt.hist(out)
plt.show()
# randn
def f03():
out=torch.randn(300,500)
# print(out,type(out),out.dtype)
# 将高维降到低维
out=out.flatten()
plt.hist(out)
plt.show()
# print(f'输出随机数种子{torch.initial_seed()}')
# 固定随机数种子
torch.manual_seed(18)
print(torch.initial_seed())
# randint 随机整型
def f04():
out=torch.randint(0,100,(10,10))
print(out,type(out),out.dtype)
# 将高维降到低维
out=out.flatten()
# plt.hist(out)
# plt.show()
if __name__ == '__main__':
# f01()
# f02()
# f03()
f04()创建全零或者全一的张量
torch.zeros(5,5) 创建五乘五的全零张量
torch.ones(5,5) 创建五乘五的全一张量
torch.full((5,5),100) 创建每个值为100的五乘五张量
torch.zeros_like 根据传入的张量形状创建全零张量
torch.ones_like 根据传入的张量形状创建全一张量
import torch
# 全零张量
def f01():
out=torch.zeros(5,5)
print(out,out.shape,out.dtype)
# 全1张量
def f02():
out=torch.ones(5,5)
print(out,out.shape,out.dtype)
# 指定值张量
def f03():
out=torch.full((5,5),100)
print(out,out.shape,out.dtype)
# like
def f04():
# 形状
tem=torch.rand(2,5)
out=torch.zeros_like(tem)
print(out,out.shape,out.dtype)
print('-'*100)
out2=torch.ones_like(tem)
print(out2,out2.shape,out2.dtype)
print('-' * 100)
out3=torch.full_like(tem,50)
print(out3,out3.shape,out3.dtype)
if __name__ == '__main__':
# f01()
# f02()
# f03()
f04()张量元素的转化:
data.type(torch.float64)
data.half()/double()/float()/short()/int()/long()
import torch
# data.type(torch.类型) 进行转化
def f01():
out=torch.rand(3,3)
print(out,out.dtype)
out2=out.type(torch.float64)
print(out2,out2.dtype)
out3=out2.type(torch.int64)
print(out3,out3.dtype)
def f02():
out=torch.rand(3,3)
print(out.dtype)
print(out.half().dtype)
print(out.double().dtype)
print(out.float().dtype)
print(out.short().dtype)
print(out.int().dtype)
print(out.long().dtype)
if __name__ == '__main__':
# f01()
f02()张量的类型转换
张量转化为numpy数组:
Tensor.numpy 浅拷贝
copy()深拷贝
# 张量转化为numpy数组
def f01():
tem=torch.randint(0,10,(3,5))
out2=tem.numpy().copy()
tem[0,0]=99
print(tem,type(tem))
out=tem.numpy()
print(out,type(out))
print(out2,type(out2))获取数字 item()
# 获取数值
def f03():
tem=torch.randn(1)
print(tem.item(),type(tem),type(tem.item()))numpy数组转化为张量:
torch_form_numpy()浅拷贝 clone()深拷贝
torch.tensor(data)深拷贝
# 数组转化为张量
def f02():
tem=np.array([1,4,7,10])
print(tem,type(tem))
out3=torch.from_numpy(tem).clone()
print(out3,type(out3))
tem[0]=5
# 转化1
out=torch.tensor(tem)
print(out,type(out))
# 转化2
out2=torch.from_numpy(tem)
print(out2,type(out2))张量的基本运算:
加减乘除 形状相同
add,sub,mul,div,neg
add_,sub_,mul_,div_,neg_的会修改原数据
**点乘:**相同形状的张量对应位置进行乘法
矩阵的乘法 @ 或者是 torch.matmul 第一个矩阵的列=第二个矩阵的行
import torch
# 基本运算 加减乘除,取反
def f01():
out=torch.tensor(1.)
out2=torch.tensor(2.)
# 运算符
print(out+out2)
print(out-out2)
print(out*out2)
print(out/out2)
# api
print(out.add(out2))
# 取反
d=torch.rand(3,4)
print(d)
print(d.neg())
# 点乘
def f02():
a=torch.randint(0,5,(2,3))
print(a)
b=torch.randint(6,10,(2,3))
print(b)
print('----------------------')
print(a*b)
print(a.mul(b))
# 叉乘
def f03():
a = torch.randint(0, 5, (3, 2))
print(a)
b = torch.randint(6, 10, (2,3))
print(b)
# print(a@b)
print(a.matmul(b))
if __name__ == '__main__':
# f01()
# f02()
f03()常见的计算函数
import torch
def f01():
# 创建张量
# 随机种子
torch.manual_seed(1)
emp=torch.randint(1,10,(3,2),dtype=torch.float64)
print(emp)
# 均值,dim=1为行的均值
print(f'行的均值为{emp.mean(dim=1)}')
# dim=0为列的均值
print(f'列的均值为{emp.mean(dim=0)}')
# 求和
print(f'行的求和为{emp.sum(dim=1)}')
print(f'列的求和为{emp.sum(dim=0)}')
# 极大值极小值
print(f'行的极大值为{emp.max(dim=1)}')
print(f'列的极大值为{emp.max(dim=0)}')
# 极小值
print(f'行的极小值为{emp.min(dim=1)}')
print(f'列的极小值为{emp.min(dim=0)}')
# 平方根
print(f'emp的平方根是{emp.sqrt()}')
# 幂运算
print(f'emp的幂运算为{emp.pow(2)}')
# 指数运算
print(f'emp的指数运算为{emp.exp()}')
# 对数运算
print(f'对数运算log为{emp.log()}')
print(f'对数运算log2为{emp.log2()}')
print(f'对数运算log10为{emp.log10()}')
if __name__ == '__main__':
f01()张量的索引和多维索引操作:
import torch
torch.manual_seed(12)
emp=torch.randint(1,10,(4,5))
# 行列倒叙
print(emp)
# dims=0 为只反转行 1 只反转列 0,1都反转
print(torch.flip(emp,[0,1]))
#
# print(emp)
# print(f'行索引{emp[1]}')
# print(f'列索引{emp[:,0]}')
# # 列表索引返回(0,1)和(1,2)两个位置的元素
# print(f'(0,1)的元素{emp[0,1]}')
# print(f'(1,2)的元素{emp[1,2]}')
# # 返回两行两列的元素
# print(f'返回第0,1两行和1,2两列的元素为{emp[0:2,1:3]}')
# # 返回范围索引的内容
# print(f'前三行的前两列数据{emp[0:3,0:2]}')
# print(f'第二行到最后的前两列的数据{emp[1:,0:2]}')
# # 布尔索引
# print(f'第三列数值大于5的完整行数据{emp[emp[:,2]>5]}')
# print(f'第二行数值大于5的元素对应的完整列数据{emp[:,emp[1,:]>5]}')
# 多维索引,创建一个 n h w 的矩阵
out=torch.randint(0,10,(3,4,5))
print(out)
print(f'获取0轴上的第一个元素{out[0]}')
print(f'获取1轴上的第一个元素{out[:,0,:]}')
print(f'获取2轴上的第一个元素{out[:,:,0]}')张量形状的改变: 都是浅拷贝
reshape: 保证张量数据不变的前提下改变数据的维度,将其转化为指定维度 -1:会自动计算剩下维度
squeeze:删除形状为1的维度
unsqueeze:在指定位置添加形状为的维度
transpose:只能交换两个维度的位置
permute:可以交换多个维度的位置
view:改变维度但是内存要连续
is_contiguous:判断内存是否连续 返回True/False
contiguous:强制内存连续
API:
import torch
# reshape:修改形状
a=torch.randn([2,3,4])
print(a.shape)
print(a.reshape(2,-1).shape)
print()
#squeeze删除维度为一的内容
a=torch.randn([1,2,3,4,1,1,2,3])
print(a.shape)
print(a.squeeze().shape)
print()
# unsqueeze 扩维,在对应位置上添加形状为1的维度
b=torch.randn([2,3,4])
out=b.unsqueeze(0)
print(out.shape)
out2=b.unsqueeze(1)
print(out2.shape)
print()
# transpose 维度交换,只能交换两个维度
a=torch.randn([2,3,4])
print(a.shape)
print(a.transpose(0,1).shape)
print(a.transpose(0,2).shape)
print()
#permute 可以交换多个张量,有几个轴填写几个数字
b=torch.randn([2,3,4,5])
print(b.shape)
print(b.permute(0,3,2,1).shape)
print(b.permute(3,1,2,0).shape)
print()
# 使用view进行改变维度
a=torch.randn([2,3,4])
print(a.shape)
print(a.view(2,-1).shape)
a=a.transpose(0,1)
print(a.is_contiguous())
a=a.contiguous()
print(a.is_contiguous())
print(a.view(3,-1).shape)张量的拼接操作:
torch.cat() :将多个张量根据指定的维度进行拼接,不改变维度数(维度的总个数不变)除拼接以外的维度要相同
torch.stack():会在一个新的维度上连接一系列张量,这会增加一个新维度,并且所有输入的张量必须完全相同 新增加维度的大小为堆叠张量的数量 形状必须相同
import torch
# 张量的拼接,除了拼接的维度可以不同,其他的维度要相同
a=torch.randn(2,3,4)
b=torch.randn(2,3,5)
print(torch.cat([a,b],2).shape)
# print(torch.cat([a,b],1).shape) 报错因为剩下的维度的形状不同
print()
# 张量的堆叠
a=torch.randn(5,4)
b=torch.randn(5,4)
c=torch.randn(5,4)
print(torch.stack([a,b],0).shape)
print(torch.stack([a,b],1).shape)
print(torch.stack([a,b],2).shape)
print(torch.stack([a,b,c],1).shape)自动微分模块:
对损失函数求导,结合自动微分模块,更新权重参数w和b
backward方法 grad属性来完成梯度的计算和访问 使用的算法是反向传播
反向传递过程:基于预测值和真实的得出误差,得到损失函数,对损失函数求导得到梯度,通过梯度的更新来反向更新权重和偏置
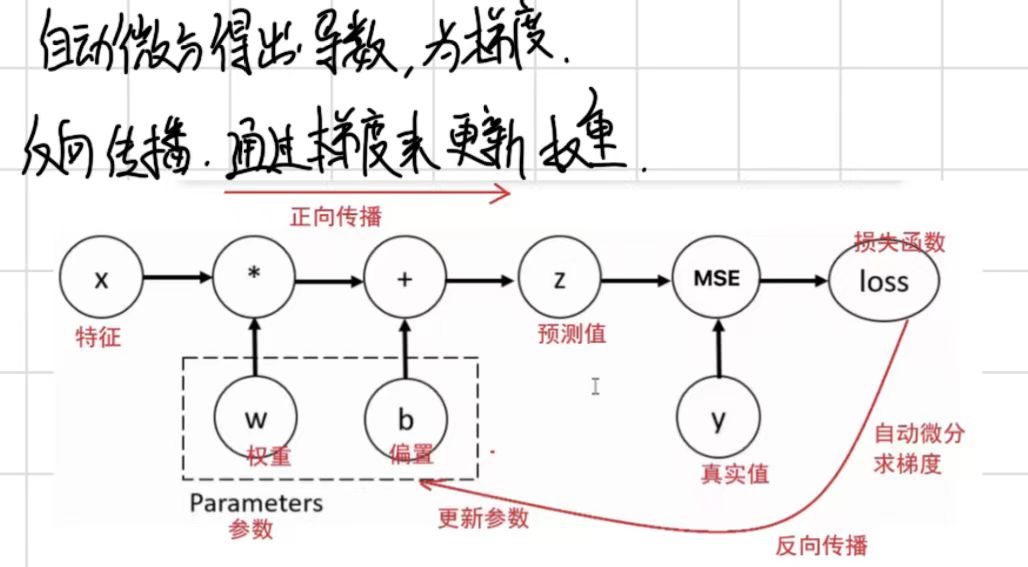
单梯度下降:
requires_grad=True,启动了自动微分模块
import torch
# 权重
w=torch.tensor([10,20],requires_grad=True,dtype=torch.float32)
# 梯度
loss=2*w**2
# 自动微分
loss.sum().backward()
# 自动计算梯度
print(f'原梯度值为{w.data},学习率为{0.01},更新后的梯度为{w.grad},下一个权重为{w.data-0.01*w.grad}')多梯度下降:
梯度会累加所以每次需要对梯度进行清零处理
import torch
# 权重
w=torch.tensor([10],requires_grad=True,dtype=torch.float32)
# 多轮梯度
epochs=500
for epoch in range(epochs):
# 损失函数
loss = w**2+20
# 梯度清零
if w.grad is not None:
w.grad.zero_()
# 自动微分
loss.sum().backward()
# 自动计算梯度
print(f'当前轮次为{epoch+1},当前权重为{w.data},学习率为{0.01},更新后的梯度为{w.grad},下一个权重为{w.data-0.01*w.grad}')
# 更新梯度
w.data=w.data-0.01*w.grad梯度基本运算:
Pytorch不支持向量张量对向量张量的求导,只支持标量张量对标量张量的求导
所以如果w是张量y必须是标量才能进行求导 loss.sum().backward() 将向量转化为张量进行计算
import torch
# 记录初始的权重
# 参数 初始值 是否自动微分,这个参数为True的时候就可以求导 参数的类型
w=torch.tensor(10,requires_grad=True,dtype=torch.float)
# 定义损失函数变量
loss=2*w**2 # 求梯度(求导) 为 4w
# 查看梯度函数的类型,即曲线函数类型
# print(type(loss.grad_fn))
#
# 计算梯度=损失函数的导数,计算完毕之后,会记录到w.grad属性中
loss.backward()
# loss.sum().backward() 保证损失函数一定是一个标量,进行求导
#
# 就是求导得出来的梯度
print(w.grad)
# 带入权重更新公式: w新=w旧 - 学习率*梯度
w.data=w.data-0.01*w.grad
print(w.data)梯度下降求最优解:
只有反向传播的时候才有梯度 先对梯度进行判断是否为空,为空进行梯度清零
import torch
# 计算梯度下降最优解就是损失函数最小,
# 定义初始权重w=10
# 参数 初始权重值 进行自动微分(求导) 数据类型
w = torch.tensor(10, requires_grad=True, dtype=torch.float32)
# 损失函数为loss=w**2+20
loss=w**2+20
# 定义学习率为0.01
# 输出初始值
print(f'初始权重为{w},(0.01*w.grad):无, loss:{loss}')
# 迭代1000次求最优解
for i in range(1,460):
# 需要更新损失函数
loss = w ** 2 + 20
# 先判断梯度是否为None
if w.grad is not None:
# 不为空就需要进行梯度清空
w.grad.zero_()
# 进行自动微分和反向传播
loss.sum().backward()
# 更新权重
w.data=w.data-0.01*w.grad
# print(f'第{i}次,权重的初始值为{w.data} (0.01*w.grad):{0.01*w.grad}),loss:{loss}')
print(f'第{i}次,权重的初始值为{w:.5f} (0.01*w.grad):{(0.01*w.grad):.5f}),loss:{loss:.5f}')
# 最终结果
print(f'最终结果为:权重:{w:.5f},梯度:{w.grad:.5f},loss:{loss:.5f}')梯度计算的注意点:不能将自动微分的张量转化为numpy数组会发生报错,使用detch()方法将张量进行拷贝
import torch
import numpy as np
# 创建张量
a=torch.tensor([[1,2,3],[4,5,6],[7,8,9]],requires_grad=True,dtype=torch.float32)
# b=a.numpy()
print(type(a))
# print(b,type(b))
a1=a.detach()
print(type(a1))
print(a.requires_grad)
print(a1.requires_grad)
print(type(a1.numpy()))
# 最终版 a1=a.detach().numpy()自动微分模块的应用:
import torch
# 特征矩阵
x=torch.ones(2,5)
# 标签矩阵
y=torch.zeros(2,3)
# 权重矩阵,需要进行自动微分
w=torch.randn(5,3,requires_grad=True)
# 偏置矩阵
b=torch.randn(3,requires_grad=True)
# 求出预测值
z=x@w+b
# 创建损失函数对象
loss_fn=torch.nn.MSELoss()
# 使用损失函数
loss=loss_fn(z,y)
print(f'loss:{loss}')
# 进行自动微分
loss.backward()
# 返回更新后的梯度
print(f'更新前的w:{w}')
print(f'更新前的b:{b}')
print(f'更新w的梯度:{w.grad}')
print(f'更新b的梯度:{b.grad}')综合案例:
1.造数据 封装为张量 将张量转化为张量数据集 再转化为数据迭代器对象 分批获取数据
2,创建回归模型对象
3,创建损失函数
4,创建优化器对象
5,外层遍历轮次,内层遍历每一批次
优化器帮我们自动更新权重和梯度使用step()函数
API:
# 导包
import torch
from torch.utils.data import TensorDataset # 构造数据集对象
from torch.utils.data import DataLoader # 数据加载器
from torch import nn # nn模块中有平方损失函数和假设函数
from torch import optim # optim模块中有优化器函数
from sklearn.datasets import make_regression # 创建线性回归模型数据集
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 创建线性回归数据集
def create_dataset():
x,y,coef=make_regression(
n_samples=100, # 100个样本
n_features=1, # 1个特征
noise=10, # 噪声,噪声越大样本点越分散,越小越密集、
coef=True, # 返回权重
bias=14.5, # 偏置
random_state=3 # 随机种子
)
# 对x,y进行数据类型的转化
x=torch.tensor(x,dtype=torch.float32)
y=torch.tensor(y,dtype=torch.float32)
return x,y,coef
# 定义函数,进行模型的训练
def train_model(x,y,coef):
# 创建数据集对象
dataset=TensorDataset(x,y)
# 创建加载器对象
# 参数: 数据集对象,每批次的样本数,是否打乱样本
dataloader=DataLoader(dataset,batch_size=16,shuffle=True)
# 创建线性模型
# 参数: 输入的特征数 输出的标签数
model=nn.Linear(1,1)
# 创建损失函数对象
criterion=nn.MSELoss()
# 创建优化器对象
# 参数 模型待调整的参数 学习率
optimizer=optim.SGD(model.parameters(),lr=0.001)
# 初始化 轮数 每轮的平均损失值 训练总损失值 训练的样本数
epochs=1000
loss_list=[]
tolal_loss=0.0
tolal_sample=0
# 循环论数
for epoch in range(epochs):
# 计算每轮的每批的损失
for x_train,y_train in dataloader:
# 模型的预测
y_pred=model(x_train)
# 计算损失
# 参数 预测值 真实值,
# 因为训练的数据为100行1列所有生成的预测值也是100行一列所有要把真实值改变形状
loss=criterion(y_pred,y_train.reshape(-1,1))
# 计算总损失和样本的批次数
# 每批次累加损失值
tolal_loss+=loss.item()
# 每使用一批进行加一
tolal_sample+=1
# 进行梯度清零,反向传播,梯度更新
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 将每轮的平均损失加入到列表中
loss_list.append(tolal_loss / tolal_sample)
print(f'轮数{epoch+1},平均损失函数为{tolal_loss/tolal_sample}')
print(f'{epochs}轮的平均损失函数为{loss_list}')
print(f'权重:{model.weight} 偏置为{model.bias}')
# 绘制损失曲线
plt.plot(range(epochs),loss_list)
plt.title('损失值曲线变化图')
plt.grid()
plt.show()
# 绘制样本点的分布
plt.scatter(x,y)
# 9.2 绘制训练模型的预测值(分离梯度并转 numpy)
y_pred = torch.tensor([(v * model.weight + model.bias).detach().numpy() for v in x])
# 9.3 计算真实值(确保为数值类型)
y_true = torch.tensor([(v * coef + 14.5).numpy() if isinstance(v, torch.Tensor) else (v * coef + 14.5) for v in x])
# 9.4 绘图时,若 x 是张量也需转 numpy
plt.plot(x.detach().numpy(), y_pred.numpy(), color='red', label='预测值')
plt.plot(x.detach().numpy(), y_true.numpy(), color='green', label='真实值')
plt.legend()
plt.grid()
plt.show()
if __name__ == '__main__':
x,y,coef=create_dataset()
# print(f'x:{x},y:{y},coef:{coef}')
# print(f'x的形状为:{x.shape},y:{y.shape},coef:{coef}')
train_model(x,y,coef)