一、为什么需要"稀疏"(Why sparse?)
许多信号在某个变换域 中呈现稀疏性:只有极少数系数不为零(或显著非零),其余系数接近于零。
典型动机与示例:
- 三个正弦波在时域 看似复杂、叠加起伏;在频域只在对应频率处出现少量冲击------系数极少,表示稀疏。
- 对于不同信号 y 1 , y 2 y_1, y_2 y1,y2,在时域呈复杂波形,但在恰当变换(如傅里叶、小波等)后,其频域/系数域多为脉冲式稀疏。
- 在过完备基(如"时间+频率"联合)下,信号通常能用更少的原子(基向量)组合起来。
- 自然数据的例子:乐器音谱、语音声谱图;自然图像在曲波/小波等域中也呈极强的稀疏性(大量系数接近 0,少量系数集中在边缘/纹理等结构处)。
二、字典学习的统一形式(Dictionary Learning)
设数据矩阵 X ∈ R d × n X\in\mathbb{R}^{d\times n} X∈Rd×n。字典学习 试图用字典 D ∈ R d × k D\in\mathbb{R}^{d\times k} D∈Rd×k 与系数/表示 R ∈ R k × n R\in\mathbb{R}^{k\times n} R∈Rk×n 近似分解:
min D ∈ D , , R ∈ R ∣ X − D R ∣ F 2 . \min_{D\in\mathcal{D},,R\in\mathcal{R}}\ |X-DR|_F^2 . D∈D,,R∈Rmin ∣X−DR∣F2.
D , R \mathcal{D},\mathcal{R} D,R 表示对字典与系数的可行域/约束(稍后分别给出不同任务下的具体约束)。
三、稀疏编码(Sparse Coding)模型
在过完备 字典( k > d k>d k>d)下,希望每个样本的系数向量尽可能稀疏 :
min D ∈ D , , R ∈ R ∣ X − D R ∣ F 2 , s.t. 每列 r i 稀疏。 \min_{D\in\mathcal{D},,R\in\mathcal{R}}\ |X-DR|_F^2 ,\quad \text{s.t. 每列 } r_i\text{ 稀疏。} D∈D,,R∈Rmin ∣X−DR∣F2,s.t. 每列 ri 稀疏。
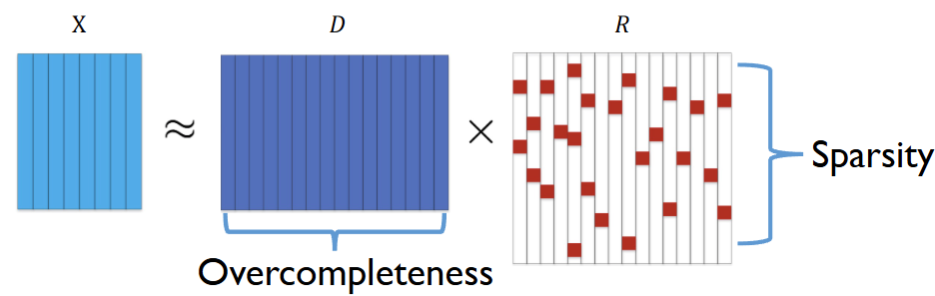
直观图示: D D D 列数多(过完备), R R R 的大部分条目为 0,仅少数非零块支撑重构。
四、 ℓ p \ell_p ℓp 范数与稀疏
向量 α ∈ R k \alpha\in\mathbb{R}^k α∈Rk 的 ℓ p \ell_p ℓp 范数:
∣ ∣ α ∣ ∣ p = ( ∑ j = 1 k ∣ α j ∣ p ) 1 / p . ||\alpha||p=\Big(\sum{j=1}^k|\alpha_j|^p\Big)^{1/p}. ∣∣α∣∣p=(j=1∑k∣αj∣p)1/p.
五、K-means 作为字典学习的特例
K-means 可写成:
min D ∈ D , , R ∈ R ∣ X − D R ∣ F 2 , \min_{D\in\mathcal{D},,R\in\mathcal{R}}\ |X-DR|_F^2 , D∈D,,R∈Rmin ∣X−DR∣F2,
其中约束为: R R R 的每一列是one-hot 向量( ∣ R i ∣ 0 = 1 |R_i|_0=1 ∣Ri∣0=1 且 ∣ R i ∣ 1 = 1 |R_i|_1=1 ∣Ri∣1=1)。
这对应"每个样本只选一个簇中心"------极端稀疏(1-sparse)。
六、K-SVD
在一般稀疏编码中,要求每列 R i R_i Ri 的非零个数受限:
min D , R ∣ X − D R ∣ F 2 , ∣ R i ∣ 0 ≤ k ′ , k ′ ≪ k . \min_{D,R}\ |X-DR|_F^2,\qquad |R_i|_0\le k',\ \ k'\ll k . D,Rmin ∣X−DR∣F2,∣Ri∣0≤k′, k′≪k.
K-SVD 交替更新:先用稀疏编码(如 OMP)求 R R R,再用 SVD 逐列更新字典原子。
七、稀疏编码的实际应用
- 图像压缩:在相同比特预算(如 820 bytes/图)下,K-SVD 等稀疏表示可较 PCA/JPEG/JPEG2000 获得更低失真(示例对比图)。
- 图像修补(Inpainting):在 70%/90% 丢样的情况下,K-SVD/DCT/Haar 进行稀疏重建,RMSE 对比显示 K-SVD 具有竞争力。
- 文本去除修补:对覆盖文字的区域以稀疏先验重建背景纹理,达到去字效果。
八、如何度量并诱导稀疏:目标函数
在字典学习统一目标上加入稀疏正则 :
min D , R ∣ X − D R ∣ F 2 + λ , ψ ( R ) , \min_{D,R}\ |X-DR|_F^2+\lambda,\psi(R), D,Rmin ∣X−DR∣F2+λ,ψ(R),
其中 ψ ( R ) \psi(R) ψ(R) 用于控制每列表示的稀疏性。问题: ψ ( ⋅ ) \psi(\cdot) ψ(⋅) 如何设计?
九、 ℓ 0 \ell_0 ℓ0 稀疏度与其难点
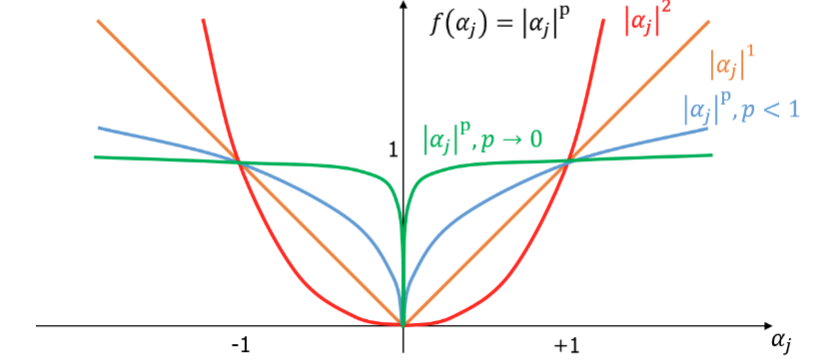
用 ℓ 0 \ell_0 ℓ0 直接计数是理想但难优化:非凸、NP-hard。
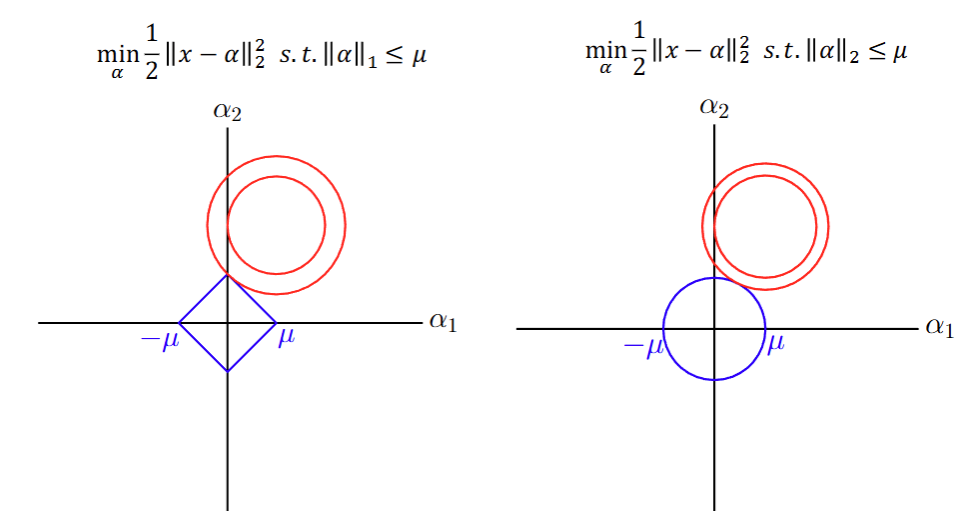
二维几何直观:如果约束 ∣ α ∣ 1 ≤ μ |\alpha|_1\le \mu ∣α∣1≤μ(左图为菱形)与 ℓ 2 \ell_2 ℓ2 球(右图为圆),与同心误差球相切的点在 ℓ 1 \ell_1 ℓ1 情形更易落在坐标轴上(促稀疏)。
十、 ℓ 1 \ell_1 ℓ1 替代与常见形式(LASSO 型)
两种标准化写法:
min α ∣ α ∣ 1 s.t. ∣ X − D α ∣ ∗ F 2 ≤ ϵ , \min_\alpha\ |\alpha|_1\ \ \text{s.t.}\ \ |X-D\alpha|*F^2\le \epsilon , αmin ∣α∣1 s.t. ∣X−Dα∣∗F2≤ϵ,
或
min ∗ α ∣ X − D α ∣ F 2 + λ ∣ α ∣ 1 . \min*\alpha\ |X-D\alpha|_F^2+\lambda|\alpha|_1 . min∗α ∣X−Dα∣F2+λ∣α∣1.
ℓ 1 \ell_1 ℓ1 是凸 的、计算上可解,且在很多条件下能近似恢复 ℓ 0 \ell_0 ℓ0 稀疏解。
L1不是处处可导的,但是可以减少维度。
十一、基于 ℓ 0 \ell_0 ℓ0 的贪心算法
目标的两种 ℓ 0 \ell_0 ℓ0 约束/约束化写法:
min α ∣ X − D α ∣ F 2 s.t. ∀ i , ∣ α ∣ ∗ 0 < L , \min_\alpha |X-D\alpha|_F^2\quad \text{s.t.}\ \forall i,\ |\alpha|*0<L, αmin∣X−Dα∣F2s.t. ∀i, ∣α∣∗0<L,
或
min ∗ α ∣ α ∣ 0 s.t. ∣ X − D α ∣ F 2 ≤ ϵ . \min*\alpha |\alpha|_0\quad \text{s.t.}\ |X-D\alpha|_F^2\le \epsilon . min∗α∣α∣0s.t. ∣X−Dα∣F2≤ϵ.
常见贪心方法:OMP(Orthogonal Matching Pursuit)、SP、CoSaMP、IHT 等。
十二、 ℓ 1 \ell_1 ℓ1 方法与贝叶斯方法
ℓ 1 \ell_1 ℓ1 系列同样对应两种形式(约束式/正则式),见上文。
贝叶斯稀疏:
- RVM(Relevance Vector Machine)
- BCS (Bayesian Compressed Sensing)
通过稀疏先验(如稀疏促性的层级高斯/拉普拉斯等)自动实现模型选择与稀疏化。
十三、正则化与算法稳定性(Regularisation & Stability)
No-Free-Lunch 提示 :朴素稀疏算法可能不稳定。
如果训练数据的轻微扰动导致算法输出的微小变化,那么学习算法就是稳定的,并且这些变化随着数据集越来越大而消失
算法稳定性 (uniform stability)定义:给训练集
S = ( X 1 , Y 1 ) , ... , ( X n , Y n ) , S i = ( X 1 , Y 1 ) , ... , ( X i ′ , Y i ′ ) , ... , ( X n , Y n ) , S={(X_1,Y_1),\ldots,(X_n,Y_n)},\quad S^i={(X_1,Y_1),\ldots,(X'_i,Y'_i),\ldots,(X_n,Y_n)}, S=(X1,Y1),...,(Xn,Yn),Si=(X1,Y1),...,(Xi′,Yi′),...,(Xn,Yn),
二者仅在第 i i i 个样本上不同。若对任意样本 ( X , Y ) (X,Y) (X,Y) 都有
∣ ℓ ( X , Y , h S ) − ℓ ( X , Y , h ∗ S i ) ∣ ≤ ϵ ( n ) , |\ell(X,Y,h_S)-\ell(X,Y,h*{S^i})|\le \epsilon(n), ∣ℓ(X,Y,hS)−ℓ(X,Y,h∗Si)∣≤ϵ(n),
且 ϵ ( n ) → 0 \epsilon(n)\to 0 ϵ(n)→0 随 n → ∞ n\to\infty n→∞,则学习算法稳定。
13.1 泛化误差的分解(关键不等式链)
对经验风险最小化器 h S h_S hS 与最优 h ∗ h^* h∗,有
R ( h S ) − min h ∈ H R ( h ) = R ( h S ) − R ( h ∗ ) ≤ 2 sup h ∈ H , ∣ R ( h ) − R S ( h ) ∣ . R(h_S)-\min_{h\in H}R(h) =R(h_S)-R(h^*) \le 2\sup_{h\in H},|R(h)-R_S(h)| . R(hS)−h∈HminR(h)=R(hS)−R(h∗)≤2h∈Hsup,∣R(h)−RS(h)∣.
这表明:泛化误差由"真实风险与经验风险的最大偏差"控制。
13.2 期望形式与稳定性
考虑期望差:
E [ R ( h S ) − R S ( h S ) ] ≤ ϵ ′ ( n ) , \mathbb{E}[R(h_S)-R_S(h_S)] \le \epsilon'(n), E[R(hS)−RS(hS)]≤ϵ′(n),
当算法对单个样本扰动"不敏感"时,上式右端随数据量增大趋小,意味着稳定 ⇒ \Rightarrow ⇒ 好的期望泛化。
13.3 ℓ 2 \ell_2 ℓ2 正则化与稳定性
L2范数正则化将使学习算法稳定,如果所使用的代理损失函数是凸的
若使用凸替代损失 ℓ \ell ℓ 且对 h h h 是 L L L-Lipschitz,输入有界 ∣ X ∣ 2 ≤ B |X|2\le B ∣X∣2≤B。考虑
h S = arg min h ∈ H 1 n ∑ i = 1 n ℓ ( X i , Y i , h ) + λ ∣ h ∣ 2 2 . h_S=\arg\min{h\in H}\ \frac1n\sum_{i=1}^n\ell(X_i,Y_i,h)+\lambda|h|_2^2 . hS=argh∈Hmin n1i=1∑nℓ(Xi,Yi,h)+λ∣h∣22.
则可得稳定性界 :
∣ ℓ ( X , Y , h S ) − ℓ ( X , Y , h S i ) ∣ ≤ 2 L 2 B 2 λ n . |\ell(X,Y,h_S)-\ell(X,Y,h_{S^i})|\ \le\ \frac{2L^2B^2}{\lambda n}. ∣ℓ(X,Y,hS)−ℓ(X,Y,hSi)∣ ≤ λn2L2B2.
13.4 证明要点(可选)
-
L-Lipschitz :
若对任意 h , h ′ h,h' h,h′ 有
∣ ℓ ( X , Y , h ) − ℓ ( X , Y , h ′ ) ∣ ≤ L , ∣ h ( X ) − h ′ ( X ) ∣ , |\ell(X,Y,h)-\ell(X,Y,h')|\le L,|h(X)-h'(X)|, ∣ℓ(X,Y,h)−ℓ(X,Y,h′)∣≤L,∣h(X)−h′(X)∣,则 ℓ \ell ℓ 关于 h h h 为 L-Lipschitz。
-
μ \mu μ-强凸(Strongly Convex) :
若
f ( y ) ≥ f ( x ) + ⟨ ∇ f ( x ) , y − x ⟩ + μ 2 ∣ x − y ∣ 2 , f(y)\ge f(x)+\langle\nabla f(x),y-x\rangle+\frac\mu2|x-y|^2, f(y)≥f(x)+⟨∇f(x),y−x⟩+2μ∣x−y∣2,等价于 μ I ⪯ ∇ 2 f ( x ) \mu I\preceq \nabla^2 f(x) μI⪯∇2f(x)。
-
两步关键不等式链(只给结论与核心步骤):
由目标的强凸性与最优性,得到
λ ∣ h S i − h S ∣ 2 ≤ R S i , λ ( h S ) − R S , λ ( h S ) + R S , λ ( h S i ) − R S i , λ ( h S i ) , \lambda|h_{S^i}-h_S|^2\ \le\ R_{S^i,\lambda}(h_S)-R_{S,\lambda}(h_S) +R_{S,\lambda}(h_{S^i})-R_{S^i,\lambda}(h_{S^i}), λ∣hSi−hS∣2 ≤ RSi,λ(hS)−RS,λ(hS)+RS,λ(hSi)−RSi,λ(hSi),进一步界为
∣ h S i − h S ∣ ≤ 2 L B λ n . |h_{S^i}-h_S|\ \le\ \frac{2LB}{\lambda n}. ∣hSi−hS∣ ≤ λn2LB.然后由 Lipschitz 条件推出
∣ ℓ ( X , Y , h S ) − ℓ ( X , Y , h S i ) ∣ ≤ L , ∣ h S − h S i ∣ , ∣ X ∣ ≤ 2 L 2 B 2 λ n . |\ell(X,Y,h_S)-\ell(X,Y,h_{S^i})| \le L,|h_S-h_{S^i}|,|X| \le \frac{2L^2B^2}{\lambda n}. ∣ℓ(X,Y,hS)−ℓ(X,Y,hSi)∣≤L,∣hS−hSi∣,∣X∣≤λn2L2B2.其中一步使用 Cauchy-Schwarz: ⟨ a , b ⟩ ≤ ∣ a ∣ , ∣ b ∣ \langle a,b\rangle\le|a|,|b| ⟨a,b⟩≤∣a∣,∣b∣。
结语式小结(按内容顺序回顾)
- 稀疏性的动机与大量实证示例 →
- 字典学习统一目标 min ∣ X − D R ∣ F 2 \min|X-DR|_F^2 min∣X−DR∣F2 →
- 稀疏编码(过完备 + 稀疏系数) →
- ℓ p \ell_p ℓp、 ℓ 0 \ell_0 ℓ0 与 ℓ 1 \ell_1 ℓ1 的稀疏诱导 →
- K-means = one-hot 稀疏、K-SVD 的字典更新 →
- 压缩/修补/去字等应用 →
- 稀疏正则统一目标 ∣ X − D R ∣ F 2 + λ ψ ( R ) |X-DR|_F^2+\lambda\psi(R) ∣X−DR∣F2+λψ(R) →
- 贪心(OMP/SP/CoSaMP/IHT)、 ℓ 1 \ell_1 ℓ1 与贝叶斯方法 →
- 正则化---稳定性---泛化: ℓ 2 \ell_2 ℓ2 正则 + 凸替代损失给出 2 L 2 B 2 λ n \frac{2L^2B^2}{\lambda n} λn2L2B2 的稳定性界。