论文信息
- 标题: Curriculum for Crowd Counting - Is it Worthy
- 作者: M. Khan, H. Menouar, R. Hamila
- 机构: 卡塔尔移动创新中心,卡塔尔大学;卡塔尔大学电气工程系
- 关键词: 人群计数, 课程学习, CNN, 密度估计
- 摘要: 本研究通过使用8种不同的人群模型和6种课程学习设置,在两个基准数据集上进行了112次实验,详细调查了课程学习在基于密度估计的人群计数中的影响。实验结果表明,课程学习可以提高模型的学习性能并缩短收敛时间。
- 原文链接: https://arxiv.org/pdf/2401.07586
摘要
深度学习技术的最新进展在多个计算机视觉问题上取得了显著性能。最近引入了一种名为课程学习(CL)的直观技术用于训练深度学习模型。令人惊讶的是,课程学习在某些任务中取得了显著改进的结果,但在其他任务中仅带来边际改进或无改进。因此,关于是否将其作为训练监督学习模型的标准方法仍存在争议。在这项工作中,我们研究了课程学习在使用密度估计方法的人群计数中的影响。我们通过使用八种不同的人群模型和六种不同的 CL 设置进行了 112 次实验来执行详细调查。我们的实验表明,课程学习提高了模型的学习性能并缩短了收敛时间。
关键词:人群计数,课程学习,CNN,密度估计。
1 引言
人群计数是计算机视觉研究中一个有趣的问题 [Khan et al., 2022, Fan et al., 2022, Gouiaa et al., 2021]。尽管早期已经提出了几种方法 [Li et al., 2008, Topkaya et al., 2014, Chen et al., 2012, Chan and Vasconcelos, 2009] 来估计图像中的人群,但目前人群计数事实上的最先进方法是使用密度估计。密度估计采用深度学习模型,如卷积神经网络(CNN),来估计图像中的人群密度。用于训练模型的真实标签是人群图像的密度图。密度图是从点标注图生成的,其中每个点(代表一个人的头部位置)与一个高斯函数进行卷积。
多年来,已经提出了几种模型来提高在基准数据集上的准确性能。值得注意的是,CrowdCNN 是 [Zhang et al., 2015] 中第一个提出的基于 CNN 的模型。CrowdCNN 是一个使用密度图预测的单列 6 层 CNN 网络。由于是单列结构,CrowdCNN 无法捕捉人群图像中头部尺寸存在的尺度变化。CrowdNet [Boominathan et al., 2016] 和 MCNN[Zhang et al., 2016] 提出了多列架构以应对尺度变化。CrowdNet 模型使用一个浅层和一个深层网络来预测不同的人群密度。MCNN 模型使用了三列 CNN 层,每层具有不同大小的卷积核,以有效捕捉尺度变化。尽管这些多列网络取得了更好的准确性,但它们在高度拥挤场景上的性能较差,主要有两个原因。首先,模型捕捉尺度变化的能力受到列数的限制。其次,这些浅层模型由于神经元数量少而很快饱和。为了解决尺度变化问题,提出了改进的模型架构,例如编码器-解码器结构,例如 TEDnet [Jiang et al., 2019], SASNet [Song et al., 2021],以及使用多尺度模块的金字塔结构,例如 MSCNN [Zeng et al., 2017], SANet [Cao et al., 2018]。对于高度拥挤场景中的人群估计,使用来自预训练模型(如 VGG-16 [Simonyan and Zisserman, 2015], ResNet [He et al., 2016], MobileNet [Sandler et al., 2018] 和 Inception [Szegedy et al., 2015])的迁移学习的模型取得了最佳结果。一些使用迁移学习的著名模型包括 CSRNet [Li et al., 2018], C-CNN [Shi et al., 2020], BL [Ma et al., 2019](VGG),MobileCount [Gao et al., 2019](MobileNet),MMCNN [Peng et al., 2020], MFCC [Gu and Lian, 2022](ResNet),SGANet [Wang and Breckon, 2022](Inception)等。
最近,课程学习(CL)作为一种改进各种深度学习任务性能的替代方法受到了显著关注。课程学习是指通过模仿人类课程来训练深度学习模型的一系列技术。在 CL 策略中,训练样本在输入模型之前按特定顺序(通常按难度递增或递减)组织。CL 最初在 [Bengio et al., 2009] 中被形式化,其灵感来源于人类在任务以有意义顺序(通常是复杂度递增顺序)呈现时学习效果更好这一事实。CL 可能带来两个好处:(i)更快的收敛和(ii)更高的准确率。
CL 已被应用于多个监督学习应用,包括目标定位 [Ionescu et al., 2016, Shi and Ferrari, 2016, Tang et al., 2018]、目标检测 [Chen and Gupta, 2015, Li et al., 2017, Sangineto et al., 2019] 和机器翻译 [Kocmi and Bojar, 2017, Platanios et al., 2019, Wang et al., 2019]。CL 也成功应用于强化学习 [Narvekar et al., 2020]。尽管 CL 在几个问题中的应用实现了改进的训练、更快的收敛和性能提升;但 [Wu et al., 2021] 的作者表明 CL 未能有益于 CIFAR10 数据集 [Krizhevsky, 2009] 上的图像分类准确率性能。最近的一些工作也将 CL 应用于人群密度估计 [Khan et al., 2023b]。
本文旨在对 CL 在计算机视觉中另一个重要任务------人群计数------中进行严格评估。人群计数使用从人群图像进行像素级回归的密度估计方法。最近,极少数工作将 CL 应用于人群密度估计,报告了在某些场景下的潜在好处。由于这些工作报告的结果仅是增量式的,本文旨在广泛调查 CL 在人群密度估计中的潜力。本文的贡献如下:
我们使用八种主流人群计数模型和六种不同的 CL 设置,在两个基准人群数据集上进行了约 112 次实验。
使用两种广泛使用的人群计数指标评估模型的性能,并比较结果以了解 CL 在何时以及在何种程度上优于标准学习。
为人群计数领域的潜在研究人员得出结论。
2 背景
课程学习(CL)定义为"在 T 个训练步骤上训练标准 C C C: C = < Q 1 , . . . Q t , . . . Q T > C=<Q_{1},...Q_{t},...Q_{T}> C=<Q1,...Qt,...QT>,使得每个标准 Q t Q_{t} Qt 是目标训练分布 P ( z ) P(z) P(z) 的重新加权" 1
Q t ( z ) = W t ( z ) P ( z ) ∀ z ∈ 训练集 D Q_{t}(z)=W_{t}(z)P(z)\quad \forall z\in \text{训练集} D Qt(z)=Wt(z)P(z)∀z∈训练集D
在公式 1 中,(i) P ( z ) P(z) P(z) 的熵逐渐增加,即 H ˉ ( Q t ) < H ( Q t + 1 ) \bar{H}(Q_{t})<H(Q_{t+1}) Hˉ(Qt)<H(Qt+1),(ii)任何示例的权重增加,即 W t ( z ) ≤ W t + 1 ( z ) W_{t}(z)\leq W_{t+1}(z) Wt(z)≤Wt+1(z),或(iii) Q T ( z ) = P ( z ) Q_{T}(z)=P(z) QT(z)=P(z) [Wang et al., 2022b]。
课程学习方法的正式描述在算法 1 中给出。

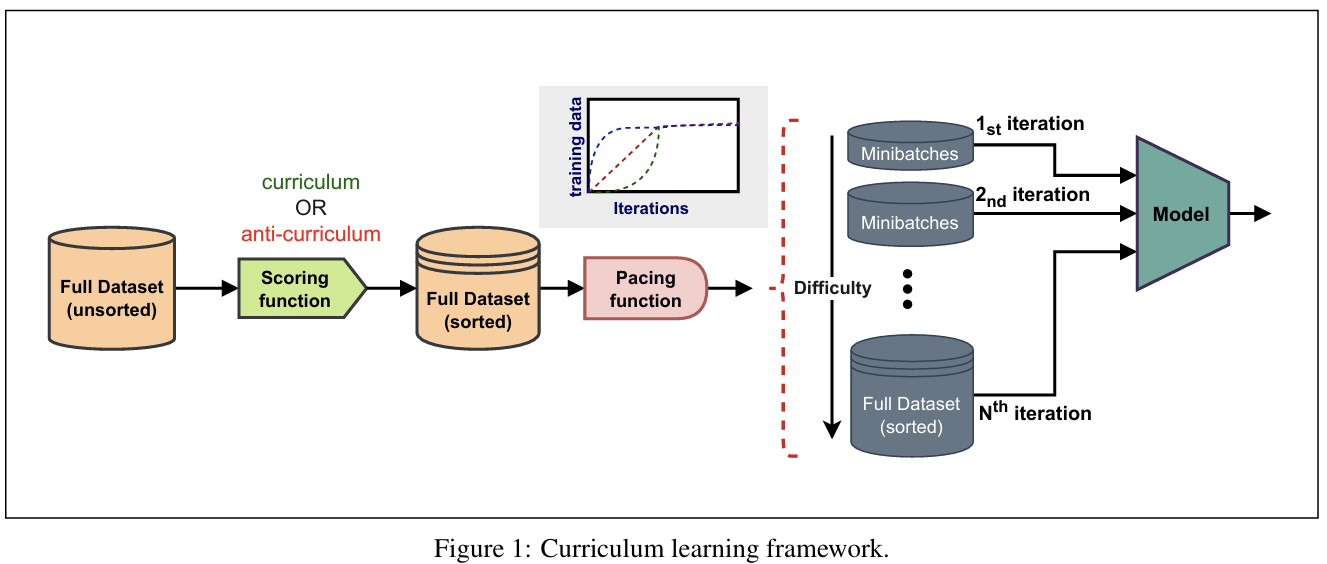
课程学习有两个主要部分:评分函数和步调函数。评分函数用于以特定的有意义顺序组织训练样本,而步调函数则在每个训练步骤中确定暴露给模型的数据量。图 1 描述了课程学习的过程。
2.1 评分函数
评分函数 (f) 是一个函数,用于按难度递增或递减的顺序对训练数据进行排序(分别对应课程学习与反课程学习)。对于给定的评分函数 f : X → R f:X \to R f:X→R,如果 f ( x i , y i ) > f ( x j , y j ) f(x_{i}, y_{i}) > f(x_{j}, y_{j}) f(xi,yi)>f(xj,yj),则 ( x i , y i ) (x_{i}, y_{i}) (xi,yi) 比 ( x j , y j ) (x_{j}, y_{j}) (xj,yj) 更难。评分函数可以通过两种方式定义:(i)自学习,或(ii)迁移评分。在自学习评分函数中,网络在均匀采样(随机排序)的批次上进行训练,以计算每个训练样本的分数(难度)。在迁移评分函数中,使用预训练模型来计算每个训练样本的分数。
2.2 步调函数
步调函数 g 是一个函数,用于确定在特定迭代中馈送给模型的训练数据子集。对于大小为 N 的训练数据 X, g : [ M ] ˉ → [ N ] g: \bar{[M]} \to [N] g:[M]ˉ→[N] 找到子集 X 1 , X 2 , . . . X M ⊂ X X_{1}, X_{2}, ... X_{M} \subset X X1,X2,...XM⊂X。从每个 X ⋅ X_{\cdot} X⋅ 中,均匀采样小批量 { B i } i = 1 M \{B_{i}\}_{i=1}^{M} {Bi}i=1M。图 2 描述了课程学习中使用的六种不同步调函数。
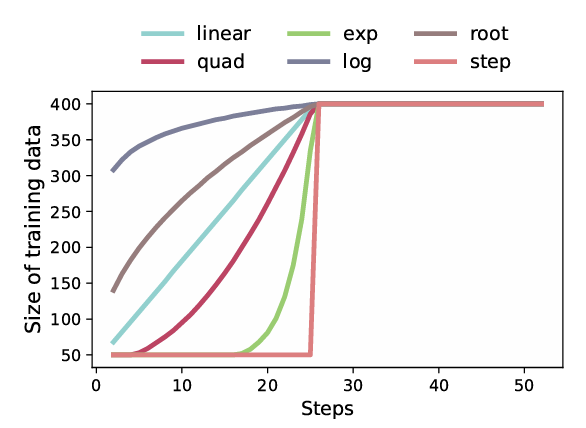
图 2:应用于 ShanghaiTech Part B 数据集的各种步调函数,总样本数 ( N ) = 400 (\mathbf{N}) = 400 (N)=400,批次大小 = 8 = 8 =8
在 CL 的更原生形式中,训练样本按难度递增顺序组织。然而,一些工作提出了反课程学习,其中训练样本按难度递减顺序组织。
3 相关工作
最近,课程学习已在少数人群计数工作中被采用。在 [Li et al., 2021] 中,作者提出 TutorNet 以改进人群计数中的密度估计。一个生成人群图像密度图的主网络在训练阶段由 TutorNet 网络监督。该网络产生一个与密度图形状相同的权重图。然后,权重图中的每个值代表模型误差的逐像素学习率。因此,该权重图被用作训练主网络的课程。TutorNet 使用 ResNet 作为前端来提取特征。该工作还使用了密度图像素值的缩放。TutorNet 在 ShanghaiTech [Zhang et al., 2016] 和 Fudan-ShanghaiTech 数据集(FDST)[Fang et al., 2019] 上进行了评估。结果显示,使用密度图缩放有显著改进,而使用 TutorNet(像素级课程)则带来进一步改进。该工作未单独考虑 TutorNet,因此对 CL 的有效性提供了很少的直观理解。[Wang et al., 2022a] 的作者遵循了类似的方法在人群计数任务中实现 CL。为人群图像中的每个像素分配一个权重,表示该像素的难度。更具体地说,首先通过平均池化操作生成区域感知密度图(RAD),然后对 RAD 应用高斯函数以产生注意力图。在注意力图中,简单的像素被分配较高的权重。提出了一种修改的损失函数,在模型训练期间使用注意力图。学习性能在 ShanghaiTech [Zhang et al., 2016], UCF-QNRF [Idrees et al., 2018], WorlExpo'10 [Zhang et al., 2015] 和 GCC [Qi et al., 2020] 数据集上进行了评估。
与许多 CL 工作中的样本级课程相比,逐像素课程的计算可能是一项更昂贵的任务。最近一项关于课程学习与数据集修剪相结合以改进学习性能和收敛时间的研究 [Khan et al., 2023a] 支持了样本级课程学习的有效性。
对上述工作的回顾为课程学习在人群计数任务中的有效性提供了有限的线索。然而,这些工作中的性能提升是课程学习的结果,还是底层人群模型的结果,还是两者共同作用的结果?课程学习是否能改进任何类型的人群模型(例如,浅层、深层、多列、编码器-解码器和多尺度,无论是否使用迁移学习)的性能?本工作旨在通过进一步调查来回答这些问题。
4 实验与评估
我们使用八种主流人群模型和两个知名数据集进行了超过 112 次实验,以研究课程学习在人群计数中的有效性。
4.1 数据集
选择的两个数据集是 ShanghaiTech Part A 和 ShanghaiTech Part B 数据集,均发表于 [Zhang et al., 2016]。这些数据集包含具有不同人群密度的跨场景人群图像,并已广泛用于众多人群计数和密度估计研究的基准测试。
4.2 基线人群模型
我们选择了八种不同的人群模型用于我们的实验。这些包括 MCNN [Zhang et al., 2016], CMTL [Sindagi and Patel, 2017], MSCNN [Zeng et al., 2017], CSRNet [Li et al., 2018], SANet [Cao et al., 2018], TEDnet [Jiang et al., 2019], Yang 等人 [Yang et al., 2020] 和 SASNet [Song et al., 2021]。选择这八种人群模型是为了使它们在模型大小、复杂性和设计上有所变化。
4.3 课程设置
我们考虑了六种不同类型的步调函数:线性、二次、指数、平方根、对数和阶梯。这些步调函数使用公式 2 计算。
g = { N b + a N b (线性) N b + N 1 − b a T t P p = 1 / 2 , 1 , 2 (二次/平方根) N b + N ( 1 − b ) e 10 − 1 ( exp ( 10 t a T − 1 ) ) (指数) N b + N ( 1 − b ) ( 1 + 1 10 log ( t a T + e − 10 ) ) (对数) N b + N [ x a T ] (阶梯) g=\left\{\begin{array}{l l}{N b+a N b}&{\text{(线性)}}\\ {N b+N\frac{1-b}{a T}t^{P} \quad p=1/2,1,2}&{\text{(二次/平方根)}}\\ {N b+\frac{N(1-b)}{e^{10}-1}\left(\exp\left(\frac{10t}{a T}-1\right)\right)}&{\text{(指数)}}\\ {N b+N\left(1-b\right)\left(1+\frac{1}{10}\log\left(\frac{t}{a T}+e^{-10}\right)\right)}&{\text{(对数)}}\\ {N b+N\left[\frac{x}{a T}\right]}&{\text{(阶梯)}}\end{array}\right. g=⎩ ⎨ ⎧Nb+aNbNb+NaT1−btPp=1/2,1,2Nb+e10−1N(1−b)(exp(aT10t−1))Nb+N(1−b)(1+101log(aTt+e−10))Nb+N[aTx](线性)(二次/平方根)(指数)(对数)(阶梯)
对于每个数据集,我们保持 b 的值固定,同时选择 a = [ 0.2 , 0.4 , 0.6 , 0.8 ] a=[0.2,0.4,0.6,0.8] a=[0.2,0.4,0.6,0.8] 的值。因此,在每次实验中,我们取完整训练数据的一小部分 (b),并根据步调函数(带参数 a)逐步添加批次。使用的步调函数如图 3 所示。
4.4 评估指标
我们使用两种常用指标来测试人群计数任务的性能,即平均绝对误差(MAE)和均方误差(MSE)。MAE 和 MSE 可以分别使用公式 3 和公式 4 计算。
M A E = 1 N ∑ n = 1 N ∣ e n − g n ∣ MAE=\frac{1}{N}\sum_{n=1}^{N}\left| e_{n}-g_{n} \right| MAE=N1n=1∑N∣en−gn∣
M S E = 1 N ∑ n = 1 N ( e n − g n ) 2 MSE=\frac{1}{N}\sum_{n=1}^{N}\left( e_{n}-g_{n} \right)^{2} MSE=N1n=1∑N(en−gn)2
其中 N 代表数据集中示例的总数, g n g_n gn 是第 n n n 张人群图像中人的实际数量, e n e_n en 是估计数量(计算为预测密度图中同一图像的像素值之和)。其他较少使用的指标包括用于更局部化计数的网格平均均值误差(GAME),以及用于预测密度图质量的结构相似性指数(SSIM)和峰值信噪比(PSNR)。
4.5 训练细节
每个人群模型首先在 ShanghaiTech Part B 数据集上使用标准训练进行训练。然后使用课程学习(使用单个步调函数)从头开始训练相同的模型。由于本研究中使用了六种步调函数,因此使用不同的步调函数对同一模型进行了六次训练。在每次实验中,我们通过检查几个周期内的相对性能(图 3)仔细选择了步调函数参数 α,以在每次迭代中定义合理的子集。因此,我们为
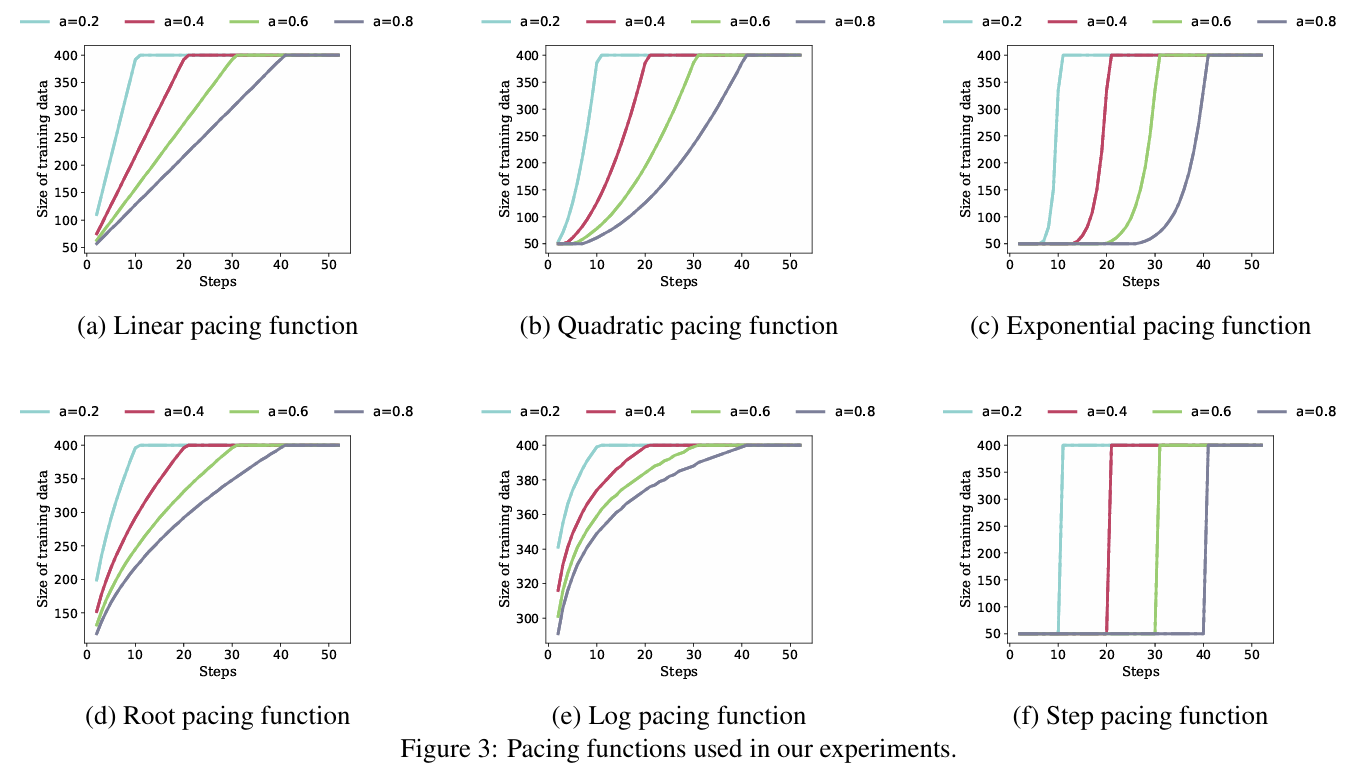
图 3:我们实验中使用的步调函数。
单个模型进行了总共七次完整训练,并在 ShanghaiTech Part B 数据集上总共进行了 56 次实验。然后对 ShanghaiTech Part A 数据集重复相同次数的实验。所有模型均使用 PyTorch 框架在两个 RTX-8000 GPU 上进行训练。在所有实验中,我们使用 Adam 优化器,初始学习率为 1 × 1 0 − 4 1 \times 10^{-4} 1×10−4,以及基于 MAE 值的 ReduceLROnPlateau 学习率衰减函数。
5 结果与分析
每次实验中训练好的模型都通过两个指标(即 MAE 和 MSE)进行评估。我们仔细选择了步调函数中的参数 a 和 b 的值,以在课程学习设置中实现合理的训练数据子集。在标准训练中,批次是从完整训练数据集中均匀采样的。每次实验中达到的最佳结果如表 1 和表 2 所示。
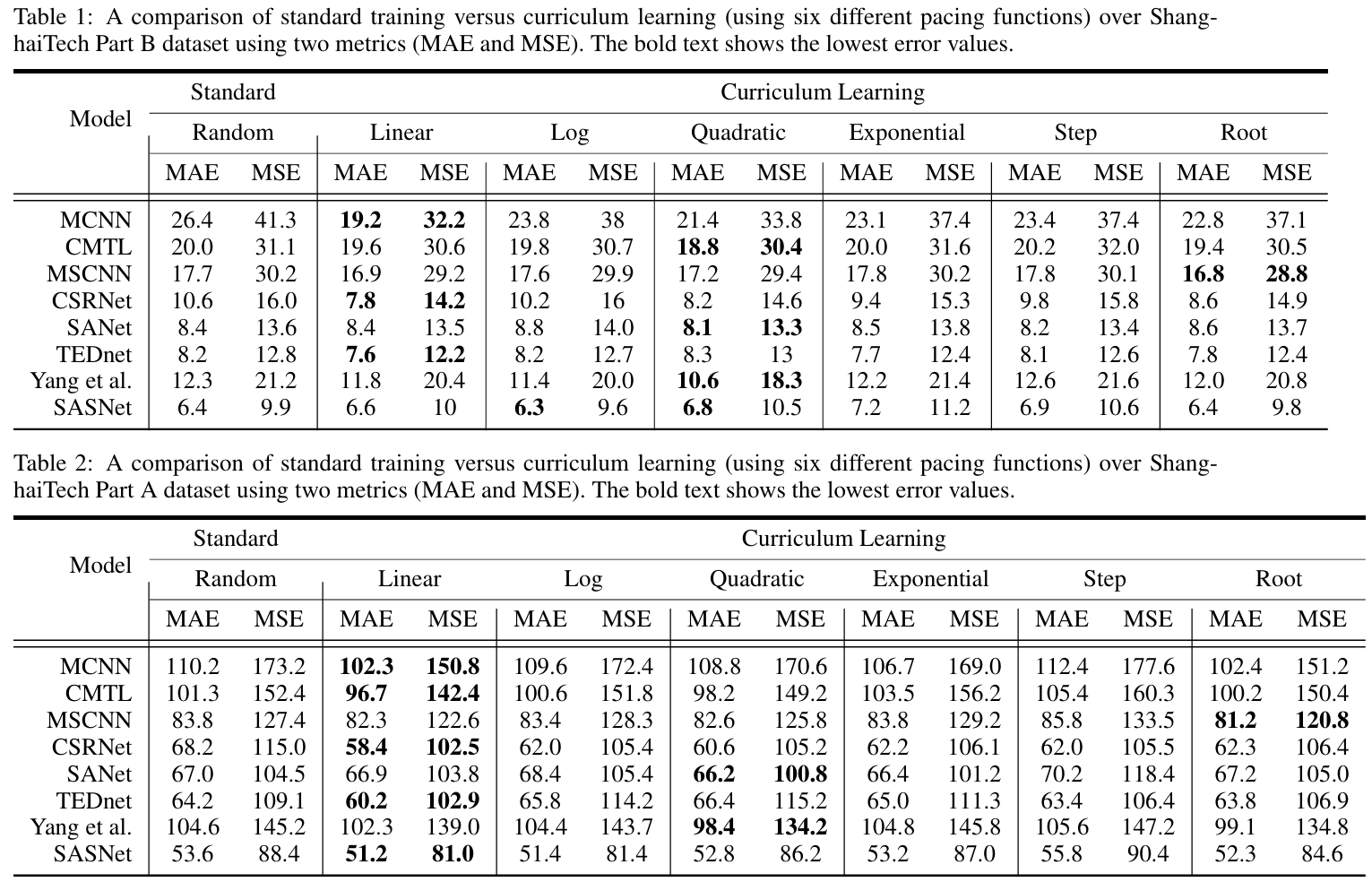
我们在结果中注意到几个有趣的观察结果。首先,课程学习在某些情况下明显带来了显著改进。例如,在 ShanghaiTech Part B 数据集上,MCNN 的 MAE 从 26.4 降至 19.2(使用线性步调函数,最佳情况)和 21.4(使用二次步调函数,次佳情况)。类似地,CSRNet 的 MAE 从 10.6 降至 7.8(使用线性步调函数)。在 ShanghaiTech Part A 数据集上,MCNN 的 MAE 从 110.2降至 102.4(线性步调函数),而 CSRNet 的 MAE 从 68.2 降至 58.4。
其次,课程学习在大多数情况下带来了边际改进。从所有模型在多个步调函数选择下的 MAE 值可以明显看出这一点。第三,课程学习在某些情况下无法改进或表现不如标准训练(在两个表中用红色字体表示)。这一观察结果凸显了步调函数作为课程学习中重要超参数的重要性。第四,课程学习的好处对于两个数据集上的所有模型都是显而易见的。然而,改进的程度因模型而异,这引发了一个合乎逻辑的问题:是什么使课程学习优于标准训练?最后一个观察结果是,每个步调函数的好处在一定程度上是一致的。例如,对于 MCNN [Zhang et al., 2016], CSRNet [Li et al., 2018] 和 TEDnet [Jiang et al., 2019],在两个数据集上,线性函数产生了最佳结果。类似地,SASNet [Song et al., 2021] 在两个数据集上使用对数步调函数产生了更好的结果。除了 SANet [Cao et al., 2018] 和 TEDnet [Jiang et al., 2019] 之外,阶梯函数几乎在所有其他步调函数上都表现不佳。
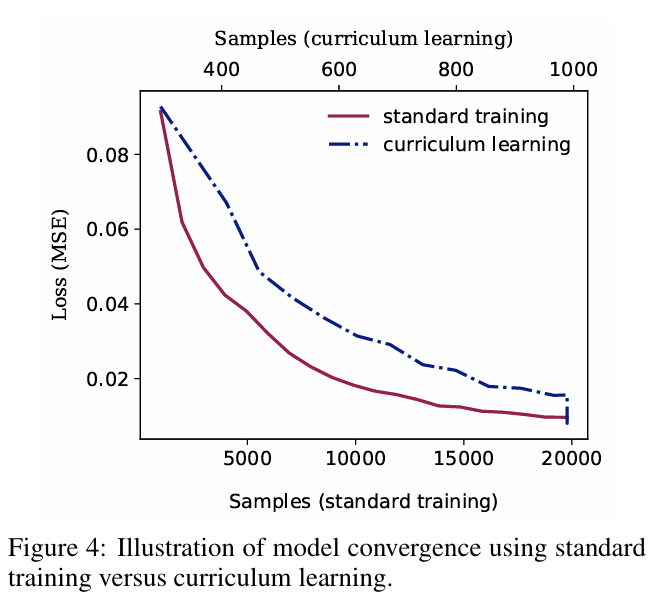
除了前面讨论的潜在显著结果外,图 4 描绘了课程学习在收敛时间方面的明显好处。y 轴显示训练阶段模型的 MSE 损失,而顶部和底部 x 轴显示在课程学习和标准训练设置期间模型看到的样本数量。与标准训练相比,课程学习中的损失下降得更快,凸显了课程学习更快的收敛速度。
6 结论
本文对人群计数中的课程学习进行了详细的实验分析。尽管课程学习在强化学习中有效,但由于缺乏详细调查,其在监督学习中的有效性尚未完全显现。我们在八种主流人群计数模型上进行了大量实验,以评估课程学习的性能。结果显示,在某些情况下有显著改进,在大多数情况下有边际改进,在少数情况下没有改进。通过对结果的详细分析,我们得出结论,通过仔细选择步调函数及其参数,课程学习有可能提高深度学习模型的性能。此外,考虑到较短的训练时间预算,课程学习是缩短收敛时间的好选择。对于未来的工作,我们建议将调查扩展到其他计算机视觉任务,使用大型数据集和适合该任务的不同评分函数。