经典算法题之子集（四）

方法二：回溯

算法

幂集是所有长度从 0 到 n 所有子集的组合。

根据定义，该问题可以看作是从序列中生成幂集。

遍历子集长度，通过回溯生成所有给定长度的子集。

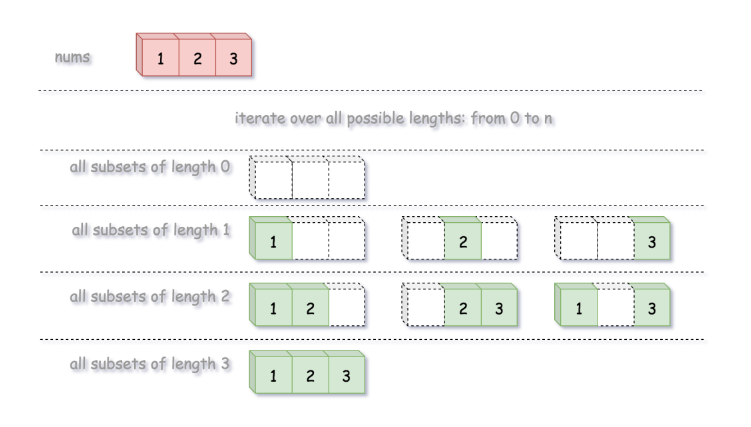
回溯法是一种探索所有潜在可能性找到解决方案的算法。如果当前方案不是正确的解决方案，或者不是最后一个正确的解决方案，则回溯法通过修改上一步的值继续寻找解决方案。

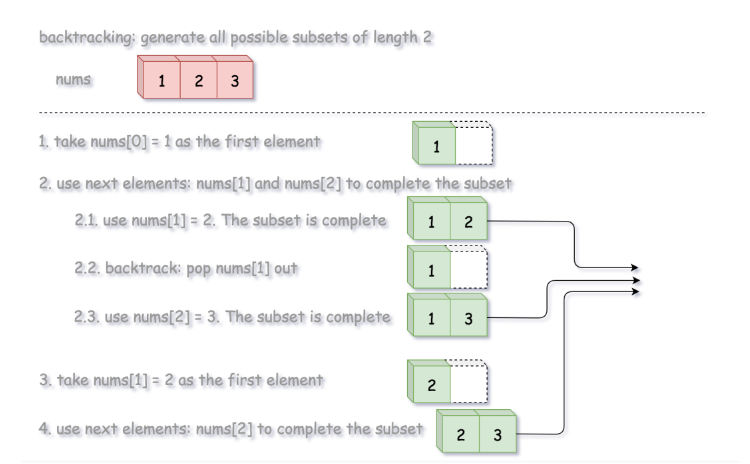
算法

定义一个回溯方法 backtrack(first, curr)，第一个参数为索引 first，第二个参数为当前子集 curr。

如果当前子集构造完成，将它添加到输出集合中。
否则，从 first 到 n 遍历索引 i。
将整数 nums[i] 添加到当前子集 curr。
继续向子集中添加整数：backtrack(i + 1, curr)。
从 curr 中删除 nums[i] 进行回溯。

Python 实现

复制代码

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        def backtrack(first = 0, curr = []):
            # if the combination is done
            if len(curr) == k:  
                output.append(curr[:])
            for i in range(first, n):
                # add nums[i] into the current combination
                curr.append(nums[i])
                # use next integers to complete the combination
                backtrack(i + 1, curr)
                # backtrack
                curr.pop()
        
        output = []
        n = len(nums)
        for k in range(n + 1):
            backtrack()
        return output

Java 实现

复制代码

class Solution {
  List<List<Integer>> output = new ArrayList();
  int n, k;

  public void backtrack(int first, ArrayList<Integer> curr, int[] nums) {
    // if the combination is done
    if (curr.size() == k)
      output.add(new ArrayList(curr));

    for (int i = first; i < n; ++i) {
      // add i into the current combination
      curr.add(nums[i]);
      // use next integers to complete the combination
      backtrack(i + 1, curr, nums);
      // backtrack
      curr.remove(curr.size() - 1);
    }
  }

  public List<List<Integer>> subsets(int[] nums) {
    n = nums.length;
    for (k = 0; k < n + 1; ++k) {
      backtrack(0, new ArrayList<Integer>(), nums);
    }
    return output;
  }
}

复杂度分析