1.概念:
Question:人工智能、机器学习、深度学习分别是什么?有什么联系?
人工智能(AI):**最终目标是让机器人像人一样"思考/决策"**例如:自动驾驶,人脸识别,聊天机器人等,让机器具有人一样的学习思考和决策能力。
机器学习(ML):本质是让机器具有学习能力---------它让机器不用被 "逐行编程",而是通过 "学习数据" 自己找规律(比如 "看 10 万张猫图,自己学会认猫",而不是程序员写 "猫有尖耳朵、圆眼睛" 的规则)。
深度学习(DL):机器学习中的一个分支,**本质是机器学习中的高级版本,专注于处理复杂数据。**核心是用 "多层神经网络" 模拟人脑的神经元连接,让机器能自动提取数据里的 "深层特征"(比如看图片时,先学边缘、再学纹理、最后学完整物体)。
机器学习:人给机器明确特征指令。
深度学习:机器自己从数据中挖取特征。
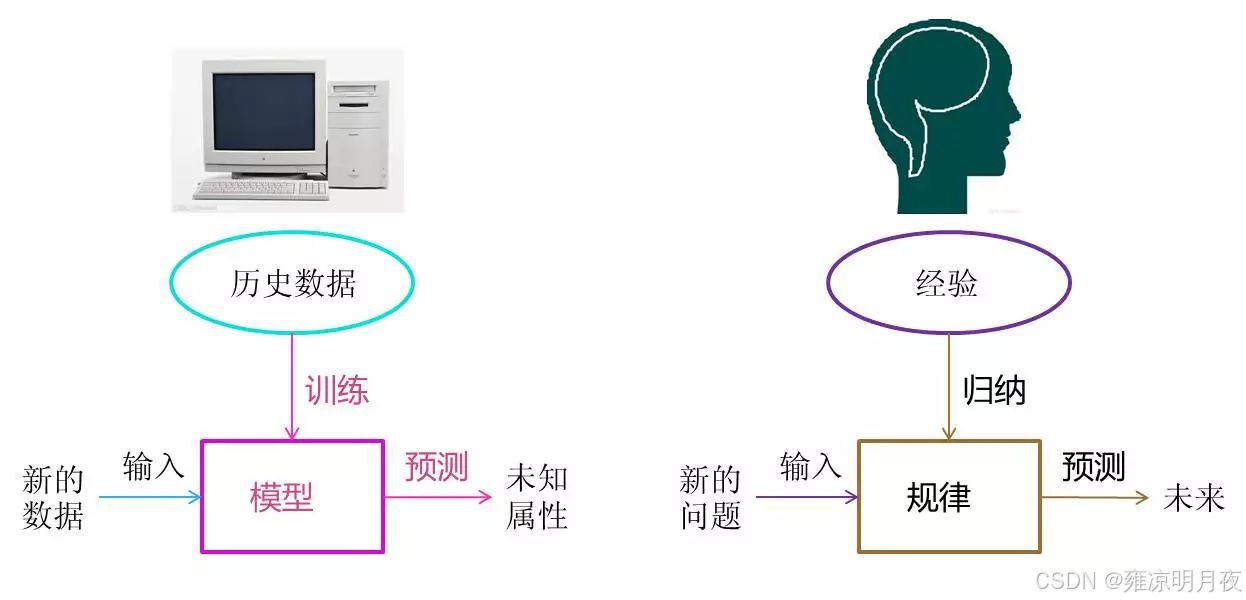
机器学习中"回归"的本质:「用现有数据,找到变量之间的函数关系(直线 / 曲线 / 特殊函数),从而预测未知的连续数值」。
- 若函数关系是直线 → 线性回归;
- 若函数关系是曲线 / 特殊函数(比如 sin、平方、指数等) → 非线性回归。
2.线性回归:
2.1本质
本质:线性回归是预测连续型因变量的监督学习模型,核心是找到一个「线性函数」,建立自变量(特征)和因变量(目标值)的关系,从而通过已知特征预测未知目标值。
- 自变量(X):用来预测的特征(比如房子面积、年限);
- 因变量(y):要预测的结果(比如房价);
- 线性函数:y = w₀ + w₁X₁ + w₂X₂ + ... + wₙXₙ(n 是特征数量)
案例:
- 单变量线性回归 :只有 1 个自变量(比如只用 "面积" 预测房价),函数是「y = w₀ + w₁X₁」(对应平面上的一条直线);
- 例子:y=1.5X₁ -2(X₁= 面积,y = 房价);
- 多变量线性回归 :有多个自变量(比如用 "面积 + 卧室数 + 楼层" 预测房价),函数是「y = w₀ + w₁X₁ + w₂X₂ + w₃X₃」(对应三维空间的平面,n 维空间的超平面);
- 例子:y= -10 + 1.2X₁(面积) + 20X₂(卧室数) - 5X₃(楼层,越低越贵)。
- 核心目标:找到一组最优的参数(w₀, w₁, ..., wₙ),使得模型预测值 ŷ(读 "y 帽")和真实值 y 的「误差最小」
2.2.线性回归的"灵魂"
灵魂------误差和损失函数。核心是「误差→损失函数→最小化损失」
误差的来源:真实值 y 和预测值 ŷ 之间的差异,叫「误差 ε」(读 "epsilon")
y = ŷ + ε → ε = y - ŷ
1.误差产生的原因:
- 模型没捕捉到的特征(比如房价还受 "学区" 影响,但没纳入模型);
- 随机噪声(比如业主急售降价、买家溢价等偶然因素)。
- 还有很多很多未考虑到的因素造成误差
2.关键假设:为了能求解最优参数,我们对误差 ε 做 3 个假设。
-
误差 ε 服从「均值为 0 的正态分布」(大多数误差围绕 0 波动,极端误差少);
-
误差 ε 的方差是常数( homoscedasticity,不会随 X 变化而变大 / 变小);
-
不同样本的误差 ε 相互独立(比如 A 房子的误差和 B 房子的误差没关系)。
-
损失函数:衡量误差的 "标尺":我们需要一个函数来量化 "所有样本的总误差",这个函数叫「损失函数」(Loss Function)。线性回归用的是「均方误差(MSE)」:
MSE = (1/m) × Σ(从 i=1 到 m)(yᵢ - ŷᵢ)²
- m:样本数量;
- yᵢ:第 i 个样本的真实值;
- ŷᵢ:第 i 个样本的预测值。
MSE的优点:
1.放大极端误差,让模型更关注减少大误差;
2.平方函数是 "凸函数",只有一个最小值,容易用数学方法找到最优解(不会陷入局部最优)。
- 核心任务:最小化损失函数
核心任务:线性回归的本质,就是找到一组参数 w(w₀, w₁, ..., wₙ),使得 MSE 最小。这个过程叫「参数估计」
计算方法1:正规方程-->直接算出最优参数
- X:特征矩阵(m 行 n+1 列),第 i 行是「1, Xᵢ₁, Xᵢ₂, ..., Xᵢₙ」(前面加 1 是为了把 w₀(截距项)纳入矩阵运算);
- y:目标值向量(m 行 1 列);
- w:参数向量(n+1 行 1 列),包含 w₀, w₁, ..., wₙ。
正规方程公式:w* = (XᵀX)⁻¹ Xᵀ y
- w*:最优参数;
- Xᵀ:X 的转置矩阵;
- (XᵀX)⁻¹:XᵀX 的逆矩阵。
例:
用之前的房价数据:
样本 i X₀(固定为 1) X₁(面积㎡) y(房价万元) 1 1 80 118 2 1 100 153 3 1 120 177 特征矩阵 X = [[1,80],[1,100],[1,120]],y = [[118],[153],[177]]计算步骤:
- XᵀX = [[3, 300], [300, 30800]](转置后相乘);
- (XᵀX)⁻¹ = 1/(3×30800 - 300×300) × [[30800, -300], [-300, 3]] → 计算得 [[154/3, -0.5], [-0.5, 3/2800]];
- Xᵀy = [[118+153+177], [80×118 + 100×153 + 120×177]] = [[448], [45380]];
- w* = (XᵀX)⁻¹ Xᵀy → 计算得 w₀≈-3.67,w₁≈1.53。
最终模型:y = -3.67 + 1.53X₁(用这个模型预测 110㎡房价:-3.67+1.53×110≈164.63 万元)。
计算方法2:梯度下降(迭代解)------适用于大数据场景
原理:
类比 "下山":你站在山上(初始参数 w),想最快走到山脚(MSE 最小值),每次都往 "坡度最陡" 的方向(梯度负方向)走一小步(学习率 α),反复迭代,直到走到山脚。
核心步骤:
- 初始化参数 w(比如全设为 0 或随机小值);
- 计算损失函数的梯度(∇MSE)------ 梯度是损失函数对每个参数 wⱼ的偏导数,表示 "参数变化 1 单位,损失变化多少";
- 更新参数:wⱼ = wⱼ - α × ∇MSE(α 是学习率,控制步长);
- 重复步骤 2-3,直到梯度接近 0(损失不再下降),此时得到最优参数 w*
- α 太小:步长太小,迭代次数太多(下山太慢);α 太大:步长太大,可能越过山脚,甚至发散(下山时一步跨到对面山坡,越走越高);实操建议:从 0.001、0.01、0.1 开始尝试,观察损失变化。
类型 原理 优点 缺点 批量梯度下降(BGD) 每次用所有样本计算梯度 收敛稳定,找到全局最优 样本量大时,计算慢 随机梯度下降(SGD) 每次用 1 个样本计算梯度 计算快,适合大数据 损失波动大,收敛不稳定 小批量梯度下降(MBGD) 每次用 k 个样本(比如 k=32、64)计算梯度 兼顾速度和稳定性 需要调参 k(批次大小)
2.3特征工程
1.特征缩放:解决特征量级差异问题
场景:梯度下降时,如果特征的量级差异太大,梯度下降会收敛很慢。
- 标准化(Z-score):X' = (X - μ)/σ(μ 是均值,σ 是标准差),缩放后特征均值为 0,方差为 1;
- 归一化(Min-Max):X' = (X - X_min)/(X_max - X_min),缩放后特征范围在 [0,1]。
经过上述办法量级达到一致,梯度下降收敛更快。
2.处理多重共线性:
场景:两个或多个特征高度相关(比如 "面积" 和 "建筑面积","体重" 和 "BMI"),会导致:
- 参数估计不稳定(比如换个样本,w₁从 1.5 变成 - 0.8);
- 模型解释性变差(不知道哪个特征真正影响 y)。
- 「方差膨胀因子(VIF)」:VIF 越大,共线性越严重
VIF 越大,共线性越严重(通常 VIF>10 认为存在严重共线性)
解决方案:
- 移除冗余特征(比如保留 "面积",删除 "建筑面积");
- 特征融合(比如用 "面积 / 卧室数" 得到 "人均面积",替代原特征);
- 正则化(L1 正则化会自动惩罚冗余特征)。
3.特征筛选:
不是特征越多越好,无用特征会增加模型复杂度,导致过拟合。
解决方法:
- 相关性分析:计算特征与 y 的皮尔逊相关系数,剔除相关系数接近 0 的特征;
- 逐步回归:从无特征开始,逐步加入对模型贡献大的特征(前向选择),或从全特征开始,逐步剔除贡献小的特征(后向消除)
4.特征转换(处理非线性关系)
如果特征和 y 是 "非线性但可转化为线性" 的关系(比如 y 和 X 是平方关系:y = w₀ + w₁X²),可以通过特征转换,用线性回归拟合:
- 平方转换:添加 X² 作为新特征;
- 对数转换:对 X 取 log(比如收入分布不均时,log (收入) 更接近线性);
- 多项式转换:添加 X²、X³、X₁X₂(交互项)等,比如 "面积 × 卧室数"(表示 "总居住空间")。
2.4 模型评估标准
1.均方误差(MSE)
- 公式:MSE = (1/m)Σ(yᵢ - ŷᵢ)²;
- 含义:平均平方误差,值越小越好(表示误差越小);
- 缺点:单位是 y 的平方(比如房价误差是 "万元 ²"),不直观。
2.均方误差(RMSE)
- 公式:RMSE = √MSE;
- 含义:平均误差的平方根,单位和 y 一致(比如房价误差是 "万元"),更直观,值越小越好。
3. 平均绝对误差(MAE)
- 公式:MAE = (1/m)Σ|yᵢ - ŷᵢ|;
- 含义:平均绝对误差,对极端值不敏感(MSE 会放大极端误差),值越小越好。
4. 决定系数(R²,最核心指标)
- 公式:R² = 1 - [Σ(yᵢ - ŷᵢ)² / Σ(yᵢ - ȳ)²](ȳ是 y 的均值);
- 含义:模型解释了多少 y 的变异(波动),范围在 [0,1]:
- R²=1:完美拟合(所有预测值 = 真实值);
- R²=0:模型和 "直接用 y 的均值预测" 一样差;
- R² 越接近 1,模型效果越好。
注意:R² 的陷阱
- 增加特征时,R² 会 "假性上升"(哪怕是无用特征);
- 解决方案:用「调整后 R²」(Adjusted R²),会惩罚多余的无用特征:
- Adjusted R² = 1 - [(1-R²)(m-1)/(m-n-1)](m = 样本数,n = 特征数)
- 只有添加 "真正有用" 的特征,Adjusted R² 才会上升。
例:
模型:y = -3.67 + 1.53X₁(X₁= 面积)样本真实值 y:[118,153,177]预测值ŷ:[-3.67+1.53×80≈118.73, -3.67+1.53×100≈149.33, -3.67+1.53×120≈179.93]计算:
- MSE = [(118-118.73)² + (153-149.33)² + (177-179.93)²]/3 ≈ (0.53 + 13.47 + 8.58)/3 ≈ 7.53;
- RMSE = √7.53 ≈ 2.74(平均误差约 2.74 万元);
- R² = 1 - [7.53×3 / ((118-149.33)² + (153-149.33)² + (177-149.33)²)] ≈ 1 - [22.6 / 1848.67] ≈ 0.987(模型解释了 98.7% 的房价变异,效果很好)。
2.5 正则化:解决过拟合
出现情况:线性回归的过拟合通常发生在:特征太多、样本太少。
**原理:**在损失函数中加入「参数惩罚项」,限制参数 w 的绝对值大小 ------ 参数越大,惩罚越重,从而避免模型过度复杂(因为复杂模型的参数通常很大)
(1)L1 正则化(Lasso 回归)
- 损失函数:Loss = MSE + λΣ|wⱼ|(λ 是正则化强度,≥0);
- 核心特点:会把不重要特征的参数 wⱼ压缩到 0,实现「自动特征筛选」(比如 λ=0.1 时,"楼层" 特征的 w=0,相当于模型自动剔除了这个特征);
- 适用场景:特征多、有冗余特征时(比如 100 个特征,只想保留 20 个有用的)。
(2)L2 正则化(Ridge 回归)
- 损失函数:Loss = MSE + λΣwⱼ²(λ 是正则化强度,≥0);
- 核心特点:不会把参数压缩到 0,只会让参数变小,避免单个特征对模型影响过大;
- 适用场景:特征少、无明显冗余,但存在轻微共线性时(比如 "面积" 和 "阳台面积" 轻度相关)。
(3)弹性网(ElasticNet)
- 损失函数:Loss = MSE + λ₁Σ|wⱼ| + λ₂Σwⱼ²(结合 L1 和 L2);
- 适用场景:特征多且存在严重共线性时(比如基因数据,上万个特征,很多高度相关)。
正则化强度 λ 的选择:
- λ=0:无正则化,就是普通线性回归;
- λ 越大:惩罚越重,参数越接近 0,模型越简单(可能欠拟合);
- λ 越小:惩罚越轻,模型越复杂(可能过拟合);
- 实操方法:用交叉验证(比如 5 折交叉验证),选择使验证集 RMSE 最小的 λ。
3.小结
本文是笔者总结了关于人工智能中机器学习和深度学习了一些基础概念,详细的讲述了机器学习中的线性回归的原理以及简单的讲述了一些关于特征的选取和模型的简单评估方法,最后对正则化解决过拟合问题也一笔带过,在之后的章节会逐步解析人工智能中的机器学习相关的算法知识,希望给大家的学习带来帮助。