01背包问题:
一. 01背包(牛客网)


01背包问题的本质就是一个商品选不选,同时注意背包的容量问题,那么状态表示一般用二维,一维来表示选不选一维来表示容量,要注意背包体积是否有剩余,完全背包问题要注意体积是否刚好合适,初始化也是采用多增加一行一列来避免越界问题
cpp
#include <iostream>
#include <cstring>
using namespace std;
const int N=1010;
int n,V,v[N],w[N];
int dp[N][N];
int main() {
//获取数据
cin>>n>>V;
for(int i=1;i<=n;i++)
cin>>v[i]>>w[i];
//解决第一问
for(int i=1;i<=n;i++)
for(int j=0;j<=V;j++)
{
dp[i][j]=dp[i-1][j];
if(j-v[i]>=0)
dp[i][j]=max(dp[i][j],dp[i-1][j-v[i]]+w[i]);
}
//第一问答案输出
cout<<dp[n][V]<<endl;
//解决第二问
memset(dp,0,sizeof(dp));
//初始化第一行为-1的情况
for(int i=1;i<=V;i++) dp[0][i]=-1;
for(int i=1;i<=n;i++)
for(int j=0;j<=V;j++)
{
dp[i][j]=dp[i-1][j];
if(j-v[i]>=0&&dp[i-1][j-v[i]]!=-1)
dp[i][j]=max(dp[i][j],dp[i-1][j-v[i]]+w[i]);
}
cout<<(dp[n][V]==-1?0:dp[n][V])<<endl;
return 0;
}- 优化版本:
已知填表需要用到上一行的信息,用完之后就没有了,所以可以极限一点,只用一行一维数组来存储,但是遍历顺序要改为从后往前,因为一维数组中,dp[j] 既存储 i-1 层的旧状态,又要存储 i 层的新状态。正序遍历 j 时,较小的 j 会先被更新为 i 层状态(选了当前物品)。当计算较大的 j 时,j - v[i] 可能指向已经更新过的 i 层状态(而非原始的 i-1 层),导致同一物品被多次计入(违背 01 背包 "每个物品只能选一次" 的规则),而逆序遍历从大的位置开始覆盖,能保证只使用上一层的旧状态 - 方法:
所有的背包问题都可以进行空间上的优化
1.直接在原始代码上修改,删除第一维数组即可
2.改变j的遍历顺序
cpp
#include <iostream>
#include <cstring>
using namespace std;
const int N=1010;
int n,V,v[N],w[N];
int dp[N][N];
int main() {
//获取数据
cin>>n>>V;
for(int i=1;i<=n;i++)
cin>>v[i]>>w[i];
//解决第一问
for(int i=1;i<=n;i++)
for(int j=0;j<=V;j++)
{
dp[i][j]=dp[i-1][j];
if(j-v[i]>=0)
dp[i][j]=max(dp[i][j],dp[i-1][j-v[i]]+w[i]);
}
//第一问答案输出
cout<<dp[n][V]<<endl;
//解决第二问
memset(dp,0,sizeof(dp));
//初始化第一行为-1的情况
for(int i=1;i<=V;i++) dp[0][i]=-1;
for(int i=1;i<=n;i++)
for(int j=0;j<=V;j++)
{
dp[i][j]=dp[i-1][j];
if(j-v[i]>=0&&dp[i-1][j-v[i]]!=-1)
dp[i][j]=max(dp[i][j],dp[i-1][j-v[i]]+w[i]);
}
cout<<(dp[n][V]==-1?0:dp[n][V])<<endl;
return 0;
}二. 分割等和子集


可以将该问题转化为背包问题,选每个数就相当于在选商品,等和子集就相当于背包容量,注意容量要是偶数才能划分否则直接返回false,注意初始化第一列可以的情况
cpp
class Solution {
public:
bool canPartition(vector<int>& nums) {
int n=nums.size();
int sum=0;
for(auto e:nums) sum+=e;
if(sum%2==1) return false;
int s=sum/2;
vector<vector<bool>>dp(n+1,vector<bool>(s+1));
//初始化
for(int i=1;i<=n;i++) dp[i][0]=1;
//填表
for(int i=1;i<=n;i++)
for(int j=1;j<=s;j++)
{
dp[i][j]=dp[i-1][j];
if(j>=nums[i-1]) dp[i][j]=dp[i][j]||dp[i-1][j-nums[i-1]];
}
return dp[n][s];
}
};空间优化:
1.删掉第⼀维;
2.修改第⼆层循环的遍历顺序即可,从后往前
cpp
class Solution {
public:
bool canPartition(vector<int>& nums) {
int n=nums.size();
int sum=0;
for(auto e:nums) sum+=e;
if(sum%2==1) return false;
int s=sum/2;
vector<bool>dp(s+1);
//初始化
dp[0]=1;
//填表
for(int i=1;i<=n;i++)
for(int j=s;j>=nums[i-1];j--)
{
dp[j]=dp[j]||dp[j-nums[i-1]];
}
return dp[s];
}
};三. (494.) 目标和


关键点在于如何转化成背包问题,后面的分析思路就比较统一,本质就是在数组中选一些数能否等于目标值。
注意初始化:
由于需要用到上⼀行的数据,因此我们可以先把第⼀行初始化。第⼀行表示不选择任何元素,要凑成目标和 j 。只有当目标和为 0 的时候才能做到,因此第⼀
行仅需初始化第⼀个元素 dp[0][0] = 1
cpp
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int s=0,sum=0;
int n=nums.size();
for(auto e:nums) s+=e;
sum=(s+target)/2;
if(sum<0||(s+target)%2==1)return 0;
vector<vector<int>>dp(n+1,vector<int>(sum+1));
dp[0][0]=1;
for(int i=1;i<=n;i++)
for(int j=0;j<=sum;j++)
{
dp[i][j]=dp[i-1][j];
if(j>=nums[i-1]) dp[i][j]+=dp[i-1][j-nums[i-1]];
}
return dp[n][sum];
}
};空间优化:
cpp
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int s=0,sum=0;
int n=nums.size();
for(auto e:nums) s+=e;
sum=(s+target)/2;
if(sum<0||(s+target)%2==1)return 0;
vector<int>dp(sum+1);
dp[0]=1;
for(int i=1;i<=n;i++)
for(int j=sum;j>=nums[i-1];j--)
{
dp[j]+=dp[j-nums[i-1]];
}
return dp[sum];
}
};四. (1049.) 最后一块石头的重量 II

可以将问题转化为01背包问题,已知任意两块石头放在一起重量相同会被丢弃,重量不同会进行差值计算并保留,也就是说任意两块石头重量相同部分会被丢弃,重量差异部分相当于在原数据前加上加减符号,所以可以将该题转化为上题目标和一样的思路
当所有元素的和固定时,分成的两部分越接近数组总和的⼀半,两者的差越小。因此问题就变成了:在数组中选择⼀些数,让这些数的和尽量接近 sum / 2 ,如果把数看成物品,每个数的值看成体积和价值,问题就变成了01 背包问题

cpp
class Solution {
public:
int lastStoneWeightII(vector<int>& s) {
int sum=0;
int n=s.size();
for(auto e:s) sum+=e;
int aim=sum/2;
vector<vector<int>>dp(n+1,vector<int>(aim+1,0));
for(int i=1;i<=n;i++)
for(int j=0;j<=aim;j++)
{
dp[i][j]=dp[i-1][j];
if(j>=s[i-1]) dp[i][j]=max(dp[i][j],dp[i-1][j-s[i-1]]+s[i-1]);
}
return sum-2*dp[n][aim];
}
};- 空间优化版本:
cpp
class Solution {
public:
int lastStoneWeightII(vector<int>& s) {
int sum=0;
int n=s.size();
for(auto e:s) sum+=e;
int aim=sum/2;
vector<int>dp(aim+1,0);
for(int i=1;i<=n;i++)
for(int j=aim;j>=s[i-1];j--)
{
dp[j]=max(dp[j],dp[j-s[i-1]]+s[i-1]);
}
return sum-2*dp[aim];
}
};完全背包问题:
五. 完全背包


- 关于空间优化01背包和完全背包的区别:
都是通过空间覆盖来减少空间消耗,区别在于遍历顺序,遍历顺序的本质是状态依赖方向。01背包怕重复选,所以从右往左保护旧状态,完全背包需要重复选,所以从左往右利用新状态
cpp
#include <iostream>
#include<cstring>
using namespace std;
const int N=1010;
int dp[N][N],v[N],w[N];
int main() {
//获取输入
int n, V;
cin>>n>>V;
for(int i=0;i<n;i++) cin>>v[i]>>w[i];
//第一题
for(int i=1;i<=n;i++)
for(int j=0;j<=V;j++)
{
dp[i][j]=dp[i-1][j];
if(j>=v[i-1])dp[i][j]=max(dp[i][j],dp[i][j-v[i-1]]+w[i-1]);
}
cout<<dp[n][V]<<endl;
//第二问
memset(dp,0,sizeof(dp));
for(int i=1;i<=V;i++)dp[0][i]=-1;
for(int i=1;i<=n;i++)
for(int j=0;j<=V;j++)
{
dp[i][j]=dp[i-1][j];
if(j>=v[i-1]&&dp[i][j-v[i-1]]!=-1)
dp[i][j]=max(dp[i][j],dp[i][j-v[i-1]]+w[i-1]);
}
cout<<(dp[n][V]==-1?0:dp[n][V])<<endl;
return 0;
}- 空间优化版本:
cpp
#include <iostream>
#include<cstring>
using namespace std;
const int N=1010;
int dp[N],v[N],w[N];
int main() {
//获取输入
int n, V;
cin>>n>>V;
for(int i=0;i<n;i++) cin>>v[i]>>w[i];
//第一题
for(int i=1;i<=n;i++)
for(int j=v[i-1];j<=V;j++)
{
dp[j]=max(dp[j],dp[j-v[i-1]]+w[i-1]);
}
cout<<dp[V]<<endl;
//第二问
memset(dp,0,sizeof(dp));
for(int i=1;i<=V;i++)dp[i]=-1;
for(int i=1;i<=n;i++)
for(int j=v[i-1];j<=V;j++)
{
if(dp[j-v[i-1]]!=-1)
dp[j]=max(dp[j],dp[j-v[i-1]]+w[i-1]);
}
cout<<(dp[V]==-1?0:dp[V])<<endl;
return 0;
}六. (322.) 零钱兑换

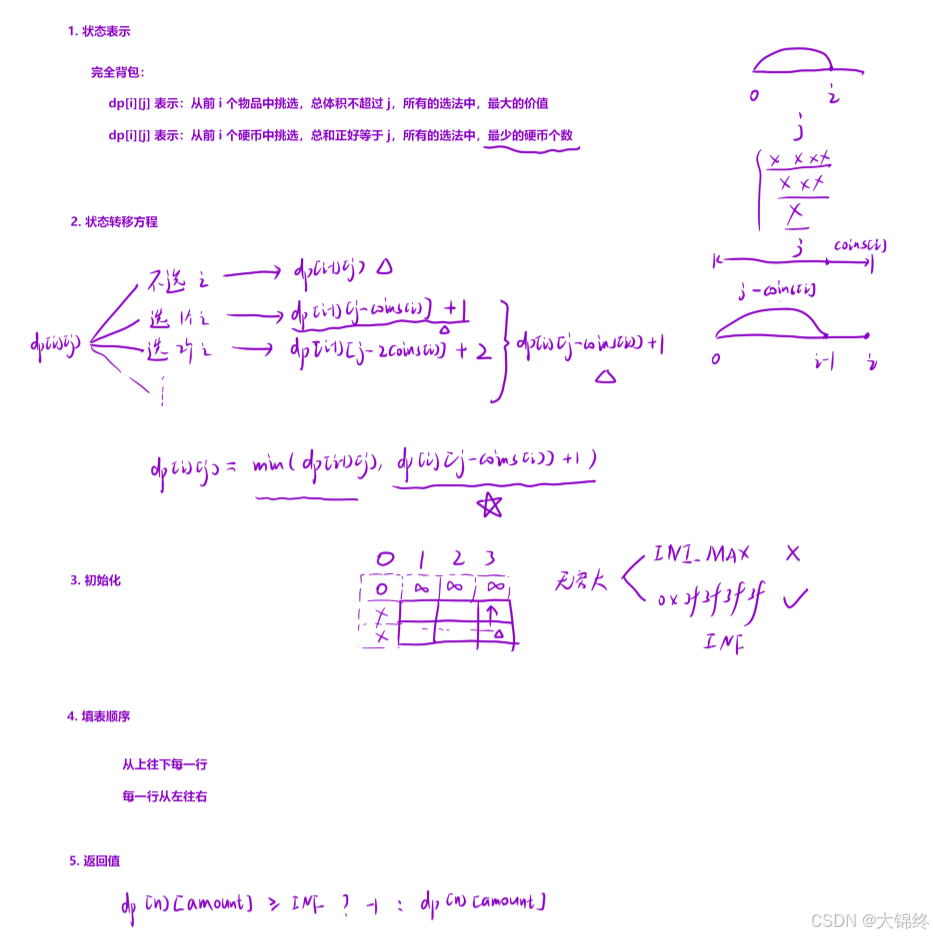
cpp
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
int n=coins.size();
vector<vector<int>>dp(n+1,vector<int>(amount+1));
//初始化
for(int i=1;i<=amount;i++) dp[0][i]=0x3f3f3f3f;
for(int i=1;i<=n;i++)
for(int j=0;j<=amount;j++)
{
dp[i][j]=dp[i-1][j];
if(j>=coins[i-1]) dp[i][j]=min(dp[i][j],dp[i][j-coins[i-1]]+1);
}
return dp[n][amount]>=0x3f3f3f3f?-1:dp[n][amount];
}
};空间优化:
cpp
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
int n=coins.size();
vector<int>dp(amount+1);
//初始化
for(int i=1;i<=amount;i++) dp[i]=0x3f3f3f3f;
for(int i=1;i<=n;i++)
for(int j=coins[i-1];j<=amount;j++)
{
dp[j]=min(dp[j],dp[j-coins[i-1]]+1);
}
return dp[amount]>=0x3f3f3f3f?-1:dp[amount];
}
};七. (518.) 零钱兑换 II

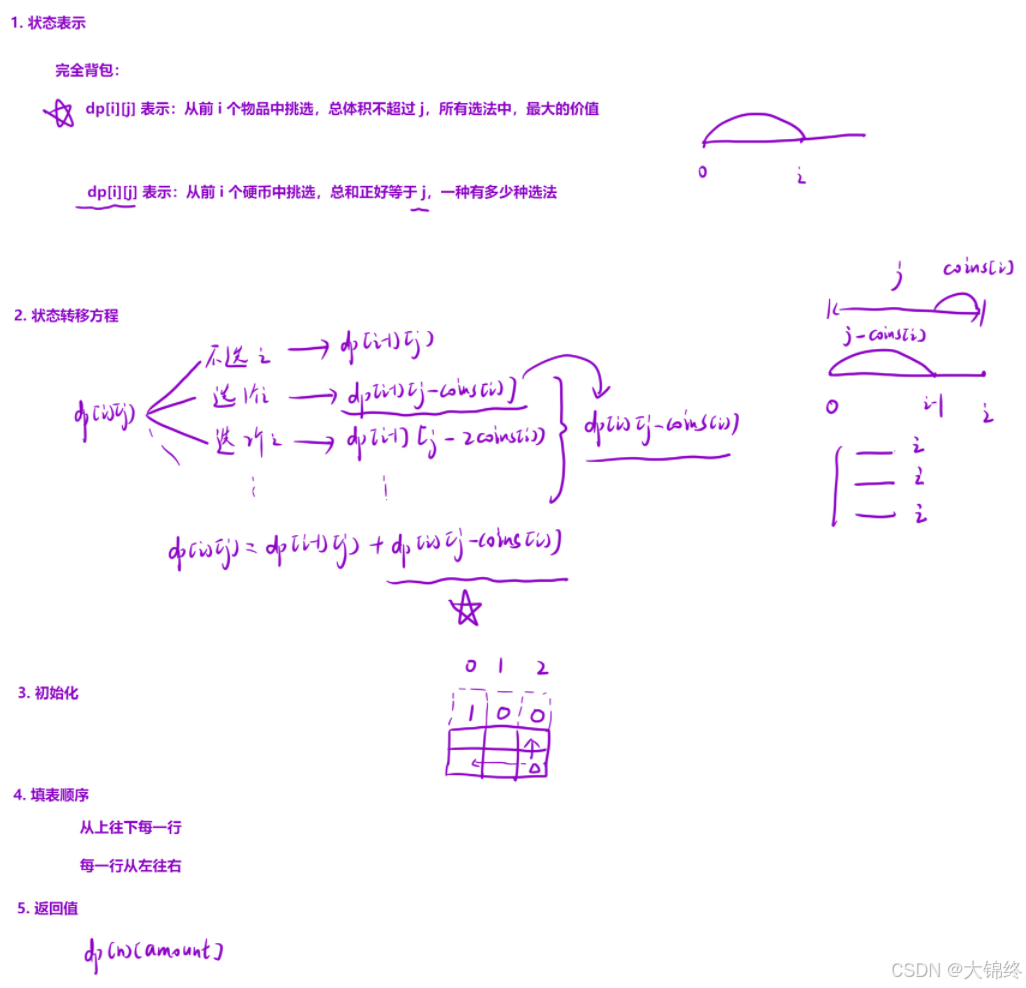
cpp
class Solution {
public:
int change(int amount, vector<int>& coins) {
int n=coins.size();
vector<vector<unsigned long long>>dp(n+1,vector<unsigned long long>(amount+1));
dp[0][0]=1;
for(int i=1;i<=n;i++)
for(int j=0;j<=amount;j++)
{
dp[i][j]=dp[i-1][j];
if(j>=coins[i-1]) dp[i][j]+=dp[i][j-coins[i-1]];
}
return dp[n][amount];
}
};八. (279.) 完全平方数


cpp
class Solution {
public:
int numSquares(int n) {
int m=sqrt(n);
vector<int>dp(n+1,0x3f3f3f3f);
dp[0]=0;
for(int i=1;i<=m;i++)
for(int j=i*i;j<=n;j++)
{
dp[j]=min(dp[j],dp[j-i*i]+1);
}
return dp[n];
}
};二维费用的背包问题:
九. (474.) ⼀和零


cpp
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
int k=strs.size();
vector<vector<vector<int>>>dp(k+1,vector<vector<int>>(m+1,vector<int>(n+1)));
for(int i=1;i<=k;i++)
{
//统计0(a)、1(b)个数
int a=0,b=0;
for(auto e:strs[i-1])
{
if(e=='0') a++;
else b++;
}
for(int j=0;j<=m;j++)
for(int x=0;x<=n;x++)
{
dp[i][j][x]=dp[i-1][j][x];
if(j>=a&&x>=b)
dp[i][j][x]=max(dp[i][j][x],dp[i-1][j-a][x-b]+1);
}
}
return dp[k][m][n];
}
};空间优化:
所有的背包问题,都可以进⾏空间上的优化
对于⼆维费⽤的 01 背包类型的,优化策略是:
i. 删掉第⼀维;
ii. 修改第⼆层以及第三层循环的遍历顺序即可
cpp
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
int k=strs.size();
vector<vector<int>>dp(m+1,vector<int>(n+1));
for(int i=1;i<=k;i++)
{
//统计0(a)、1(b)个数
int a=0,b=0;
for(auto e:strs[i-1])
{
if(e=='0') a++;
else b++;
}
for(int j=m;j>=a;j--)
for(int x=n;x>=b;x--)
dp[j][x]=max(dp[j][x],dp[j-a][x-b]+1);
}
return dp[m][n];
}
};十. (879.) 盈利计划


第三维盈利越多越好肯定,所以k-price[i-1]可能会小于0,但是数组下标不能用负数来表示,所以用0来统一表示下标为负数的情况,取max如果盈利目标-当前盈利小于0就取0,大于0就取本身
cpp
class Solution {
public:
int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit) {
const int mod=1e9+7;
int m=group.size();
vector<vector<vector<int>>>dp(m+1,vector<vector<int>>(n+1,vector<int>(minProfit+1)));
//初始化,选择为空集的情况
for(int i=0;i<=n;i++) dp[0][i][0]=1;
//填表
for(int i=1;i<=m;i++)
for(int j=0;j<=n;j++)
for(int k=0;k<=minProfit;k++)
{
dp[i][j][k]=dp[i-1][j][k];
if(j>=group[i-1])
dp[i][j][k]+=dp[i-1][j-group[i-1]][max(0,k-profit[i-1])];
dp[i][j][k]%=mod;
}
return dp[m][n][minProfit];
}
};空间优化:
cpp
class Solution {
public:
int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit) {
const int mod=1e9+7;
int m=group.size();
vector<vector<int>>dp(n+1,vector<int>(minProfit+1));
//初始化,选择为空集的情况
for(int i=0;i<=n;i++) dp[i][0]=1;
//填表
for(int i=1;i<=m;i++)
for(int j=n;j>=group[i-1];j--)
for(int k=minProfit;k>=0;k--)
{
dp[j][k]+=dp[j-group[i-1]][max(0,k-profit[i-1])];
dp[j][k]%=mod;
}
return dp[n][minProfit];
}
};似包非包问题:
十一.(377.) 组合总和 Ⅳ


- 背包问题本质求的是组合问题,是无序的,该题是排列问题,是有序的,不能用背包问题的思路来解决,用常规的动规思路来解决.dp[i]通过最后一个元素的位置,依次遍历整个原数组,若小于当前索引值就把dp[i-1]的情况累加起来
cpp
class Solution {
public:
int combinationSum4(vector<int>& nums, int target) {
vector<double>dp(target+1);
dp[0]=1;
for(int i=1;i<=target;i++)
for(auto e:nums)
if(i>=e) dp[i]+=dp[i-e];
return dp[target];
}
}; 十二. (96.) 不同的二叉搜索树
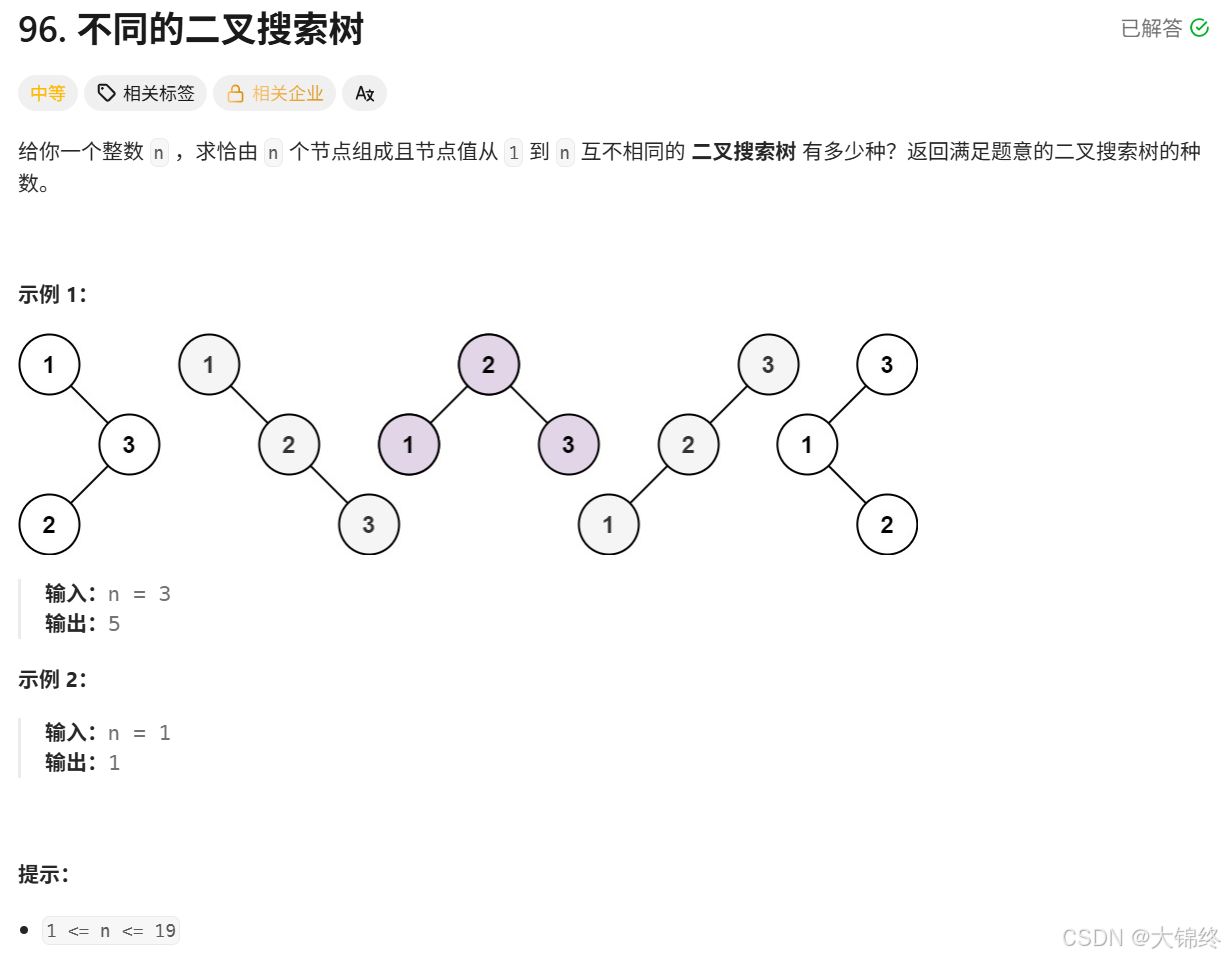

从1到当前下标位置依次遍历每一个元素作为根节点时有多少个二叉树。
外层循环 i 表示 "当前要组成的 BST 有 i 个节点(用 1到i 这 i 个数)";内层循环 j 表示 "选择 j 作为当前 BST 的 根节点"(j 必须是 1到i 中的某个数,因为 BST 的节点值是 1~i 连续的),0不能当作根节点,与题目要求不符,不是合法节点值,也会造成左子树计算越界
cpp
class Solution {
public:
int numTrees(int n) {
vector<int>dp(n+1);
dp[0]=1;
for(int i=1;i<=n;i++)
for(int j=1;j<=i;j++)
dp[i]+=dp[j-1]*dp[i-j];
return dp[n];
}
};总结:
- 关于状态转移方程的优化:
- 01背包:
商品只能选一次,依赖上一层的商品状态,所以状态转移方程一般形如:
dp[i][j]=max(dp[i][j],dp[i-1][j-v[i]]+w[i]) - 完全背包:
可以重复选择商品,所以可以依赖当前层状态,由于重复选择所以无法穷尽状态转移方程,可采用数学等价替换的方式来优化表达式。一般完全背包的优化方式如下:

- 关于空间优化:
- 01背包:
将第一维去掉,利用滚动数组的方式来覆盖计算。改变遍历顺序,从右往左,因为只能选一次商品,依赖上一层的状态,如果从左往右计算可能导致状突被提前覆盖,从右往左就不会 - 完全背包:
将第一维去掉,利用滚动数组的方式来覆盖计算。遍历顺序可以不用改变,因为可以重复选商品,所以不怕当前层元素被覆盖