郑州轻工业大学2025天梯赛解题

前言

嗨(✪ω✪)！我们又见面啦！在本专栏我将分享我遇到的编程题

文章目录

• 前言
• 第一阶段
• • [1-1 加油](#1-1 加油)
  • [1-2 车辆的运动（比较）](#1-2 车辆的运动（比较）)
  • [1-3 三年之约（比较）](#1-3 三年之约（比较）)
  • [1-4 凡事问AI](#1-4 凡事问AI)
  • [1-5 数学的进步](#1-5 数学的进步)
  • [1-6 时间计算](#1-6 时间计算)
  • [1-7 AI来做题](#1-7 AI来做题)
  • [1-8 奇变偶不变（枚举或前缀和）](#1-8 奇变偶不变（枚举或前缀和）)
  • • 暴力枚举
    • 前缀和
• 第二阶段
• • [2-1 堵塞的校园网（二次函数）](#2-1 堵塞的校园网（二次函数）)
  • [2-2 熊孩子开关灯（枚举或差分+前缀和）](#2-2 熊孩子开关灯（枚举或差分+前缀和）)
  • • 暴力枚举
    • 差分+前缀和
  • [2-3 吕布骑草履虫（排序）](#2-3 吕布骑草履虫（排序）)
  • [2-4 数学的退步（字符串）](#2-4 数学的退步（字符串）)
• 第三阶段
• • [3-1 数学题吗?（双指针/滑动窗口）](#3-1 数学题吗?（双指针/滑动窗口）)
  • [3-2 信号基站的最小干扰中转方案（暴力枚举/数位独立）](#3-2 信号基站的最小干扰中转方案（暴力枚举/数位独立）)
  • • 1、暴力枚举
    • 2、超级优化（数位独立）
  • [3-3 链表奇偶拆分（模拟）](#3-3 链表奇偶拆分（模拟）)
• 总结

个人主页：星轨初途

个人专栏：C语言，数据结构，C++学习（竞赛类） 算法及编程题分享

第一阶段

1-1 加油

输出就行

#include<bits/stdc++.h>
using namespace std;
int main()
{
     cout<<"大家加油!!!";
    return 0;
}

1-2 车辆的运动（比较）

比较一下，就出来啦！

#include<bits/stdc++.h>
using namespace std;
int main()
{
     int a,b;
    cin>>a>>b;
    if(a<b)cout<<"Speed up";
    else if(a==b)cout<<"Steady speed";
    else cout<<"Slow down";
    return 0;
}

1-3 三年之约（比较）

这个也是比较一下

#include<bits/stdc++.h>
using namespace std;
int main()
{
     int a,b,c,d;
    cin>>a>>b>>c>>d;
    if(a>=b+c+d)cout<<"莫欺少年穷"<<endl;
    else cout<<"再给我三年时间";
    return 0;
}

1-4 凡事问AI

比较一下就行

#include<bits/stdc++.h>
using namespace std;
int main()
{
     int a,b,c;
    cin>>a>>b>>c;
    int max1=a;
    max1=max(max1,b);
    max1=max(max1,c);
    int p=0;
    if(max1==a)p++;
    if(max1==b)p++;
    if(max1==c)p++;
    if(p>1)cout<<"多种原因"<<endl;
    else
    {
        if(max1==a)cout<<"打游戏";
        if(max1==b)cout<<"刷短视频";
        if(max1==c)cout<<"网上聊天";
    }
    return 0;
}

1-5 数学的进步

这个就是找出最大，和剩余的比较

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        int n;cin>>n;
        int num=0;
        int max1=-1;
        for(int i=1;i<=n;i++)
        {
            int x;cin>>x;
            max1=max(max1,x);
            num+=x;
        }
        if(!(max1>=num-max1))cout<<"Yes"<<endl;
        else cout<<"No"<<endl;
    }
    return 0;
}

1-6 时间计算

这个就是时间的相加，就是先把需要加的时间先加到分钟上，再/60加到小时上并%24

分钟就是自身再%60

#include<bits/stdc++.h>
using namespace std;
int main()
{
     int t;cin>>t;
    while(t--)
    {
        int h,m,ad;
        cin>>h>>m>>ad;
        m=m+ad;
        int p=0;
        if(m>=60)
        {
            p=m/60;
            m=m%60;
        }
        h=(h+p)%24;
        
        cout<<h<<" "<<m<<endl;
    }
    return 0;
}

1-7 AI来做题

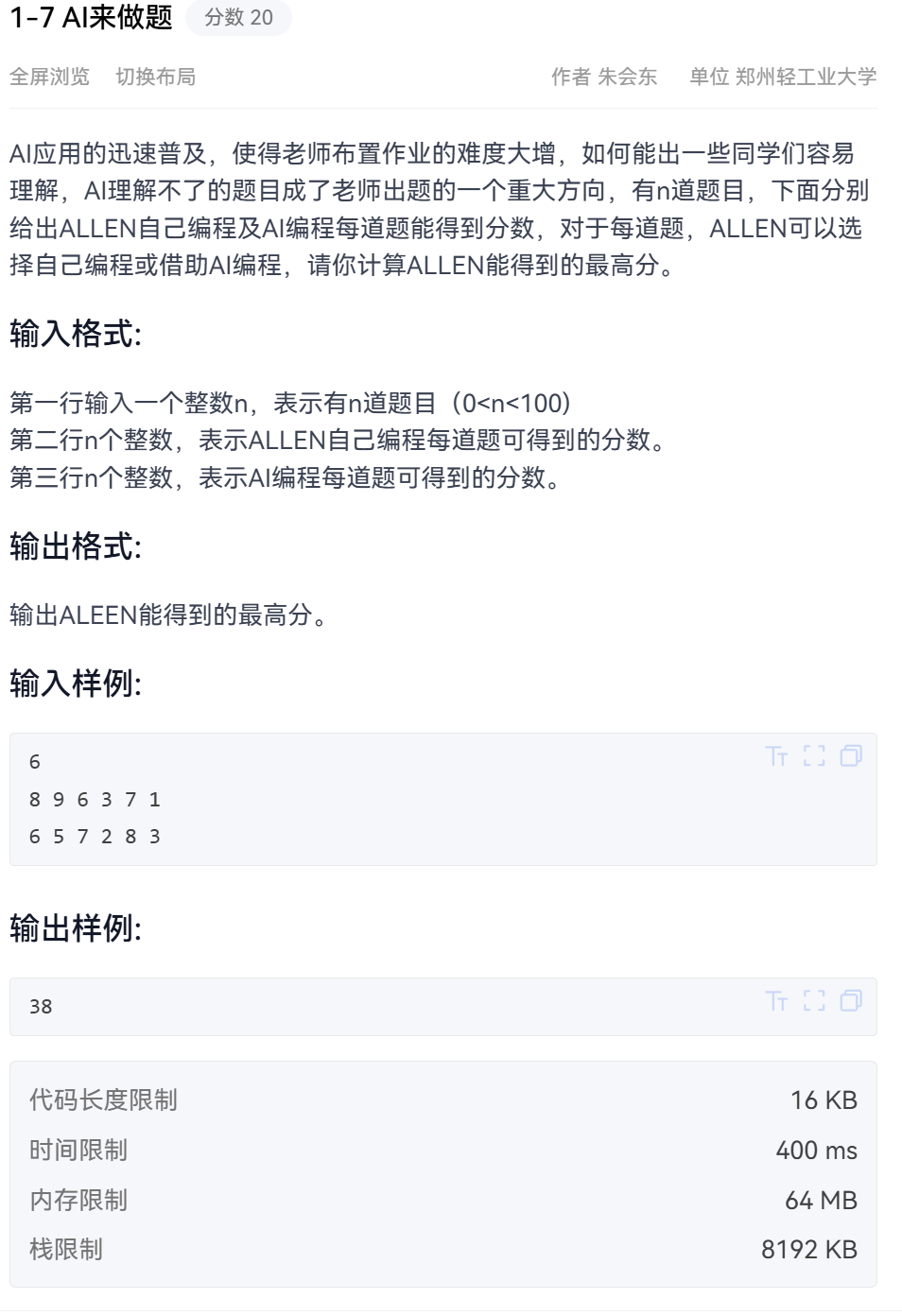
这个就是找每题AI和自己做最大值，相加

#include<bits/stdc++.h>
using namespace std;
int main()
{
     int t;cin>>t;
    int arr[t],brr[t];
    for(int i=0;i<t;i++)cin>>arr[i];
    for(int i=0;i<t;i++)cin>>brr[i];
    int num=0;
    for(int i=0;i<t;i++)
    {
        num+=max(arr[i],brr[i]);
    }
    cout<<num<<endl;
    return 0;
}

1-8 奇变偶不变（枚举或前缀和）

这个就是按照他的杀招范围，进行伤害，我们发现k的值很小，所以可以直接暴力枚举，或者用前缀和

暴力枚举

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10;
ll arr[N];
int main()
{
    ll n,x;cin>>n>>x;
    for(int i=1;i<=n;i++)cin>>arr[i];
    ll k;cin>>k;
    while(k--)
    {
        int l,r;
        cin>>l>>r;
        for(int i=l;i<=r;i++)arr[i]-=x;
        
    }
    int flag=0;int num=0;
    for(int i=1;i<=n;i++)
    {
        if(arr[i]>0)num++;
    }
    if(num==0)cout<<"YES"<<endl;
    else cout<<num<<endl;
    return 0;
}

前缀和

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10;
ll arr[N];ll brr[N];
int main()
{
    ll n,x;cin>>n>>x;
    for(int i=1;i<=n;i++)cin>>arr[i];
    ll k;cin>>k;
    while(k--)
    {
        int l,r;
        cin>>l>>r;
        brr[l]+=x;brr[r+1]-=x;
    }
    for(int i=1;i<=n;i++)
    {
        brr[i]=brr[i-1]+brr[i];
        arr[i]-=brr[i];
    }
    int flag=0;int num=0;
    for(int i=1;i<=n;i++)
    {
        if(arr[i]>0)num++;
    }
    if(num==0)cout<<"YES"<<endl;
    else cout<<num<<endl;
    return 0;
}

第二阶段

2-1 堵塞的校园网（二次函数）

这个就是二次函数

• 设总操作次数为q，单次扩容的带宽增量为b；
• 选择先扩容k次（操作二），再下载q - k次（操作一）（注：先扩容再下载是最优策略------若中途穿插下载，带宽未达最大值，下载量会更少）；
• 扩容k次后，带宽为b × k（初始带宽为0，每次扩容加b，共加k次）；
• 每次下载操作的下载量 = 当前带宽，因此总下载量 = 带宽 × 下载次数 = b × k × (q - k)。

利用我们二次函数性质，对称轴最大

当q为偶数时，k=q/2最大

当q为奇数时，k=q/2或k=(q+1)/2最大

由于二次函数对称性，当q为奇数时，k=q/2或k=(q+1)/2相等，所以这里我们直接用k=q/2啦

#include <bits/stdc++.h>
using namespace std;
int main() 
{
    int t;
    cin >> t;
    while (t--) 
    {
        int b, q;
        cin >> b >> q;
        if (b == 0 || q == 0) 
        {
            cout << 0 << endl;
            continue;
        }
        int k = q / 2;
        cout << b * k * (q - k) << endl;
    }
    return 0;
}

2-2 熊孩子开关灯（枚举或差分+前缀和）

很明显，这道题就是遍历所有开关所控制的灯,看哪些灯被2个以上开关同时控制

我们利用二维数组来解这道题，每个开关遍历二维数组+1,看谁最后>=2即可

我们发现b<=20，数据小，所以我们还可以利用暴力枚举，当然我们也可以用差分和前缀和来写

暴力枚举

#include<bits/stdc++.h>
using namespace std;
const int N = 110;
int arr[N][N];
int main()
{
    int n;
    cin >> n;
    int t; cin >> t;
    int pp = t;
    while (t--)
    {
        int x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2;
  
        for (int i = x1; i <= x2; i++)
        {
            for (int j = y1; j <= y2; j++)
            {
                arr[i][j]++;
            }
        }
    }
    int num = 0;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
  
            if (arr[i][j] >= 2)num++;
        }
    }
    if (num > n * n)num = n * n;
    cout << num << endl;
    return 0;
}

差分+前缀和

#include<bits/stdc++.h>
using namespace std;
const int N=110;
int arr[N][N];
int main()
{
    int n;
    cin>>n;
    int t;cin>>t;
    int pp=t;
    while(t--)
    {
        int x1,y1,x2,y2;cin>>x1>>y1>>x2>>y2;
        arr[x1][y1]++;
        arr[x1][y2+1]--;
        arr[x2+1][y1]--;
        arr[x2+1][y2+1]++;
    }
    int num=0;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            arr[i][j]=arr[i-1][j]+arr[i][j-1]-arr[i-1][j-1]+arr[i][j];
            if(arr[i][j]>=2)num++;
        }
    }
    if(num>n*n)num=n*n;
    cout<<num<<endl;
    return 0;
}

2-3 吕布骑草履虫（排序）

按照题目要求排序即可，我们通过样例可以看出处理器性能指数越大性能越小

#include<bits/stdc++.h>
using namespace std;
typedef struct
{
    string name;
    int p;
}ST;
bool comp(ST&a,ST&b)
{
    return a.p>b.p;
}
bool comp1(ST&a,ST&b)
{
    return a.p<b.p;
}
int main()
{
     int n;cin>>n;
    ST arr[n];
    ST brr[n];
    for(int i=0;i<n;i++)cin>>arr[i].name>>arr[i].p;
     for(int i=0;i<n;i++)cin>>brr[i].name>>brr[i].p;
    sort(arr,arr+n,comp1);sort(brr,brr+n,comp);
    ST crr[n];
    for(int i=0;i<n;i++)
    {
        crr[i].name=arr[i].name+" "+brr[i].name;
        crr[i].p=arr[i].p+brr[i].p;
    }
    for(int i=0;i<n;i++)
    {
        cout<<crr[i].name<<endl;
    }
    return 0;
}

2-4 数学的退步（字符串）

本道题原理十分简单，就是把两个数中2->5,5->2，在相加，得到的数再进行一次转换

这里我们把它转换为字符串进行操作，代码如下

#include<bits/stdc++.h>
using namespace std;
string swap25(string s)
{
    int len = s.size();
    for(int i=0;i<len;i++)
    {
        if(s[i]=='2')s[i]='5';
        else if(s[i]=='5')s[i]='2';
    }
    return s;
}
int main()
{
    int t;cin>>t;
    while(t--)
    {
        int num=0;
        string a,b;cin>>a>>b;
        a = swap25(a);
        b = swap25(b);
        int a1=stoi(a,NULL,10);
        int b1=stoi(b,NULL,10);
        num=a1+b1;
        string ll=to_string(num);
        ll = swap25(ll);
        cout<<ll<<endl;
    }
    return 0;
}

第三阶段

3-1 数学题吗?（双指针/滑动窗口）

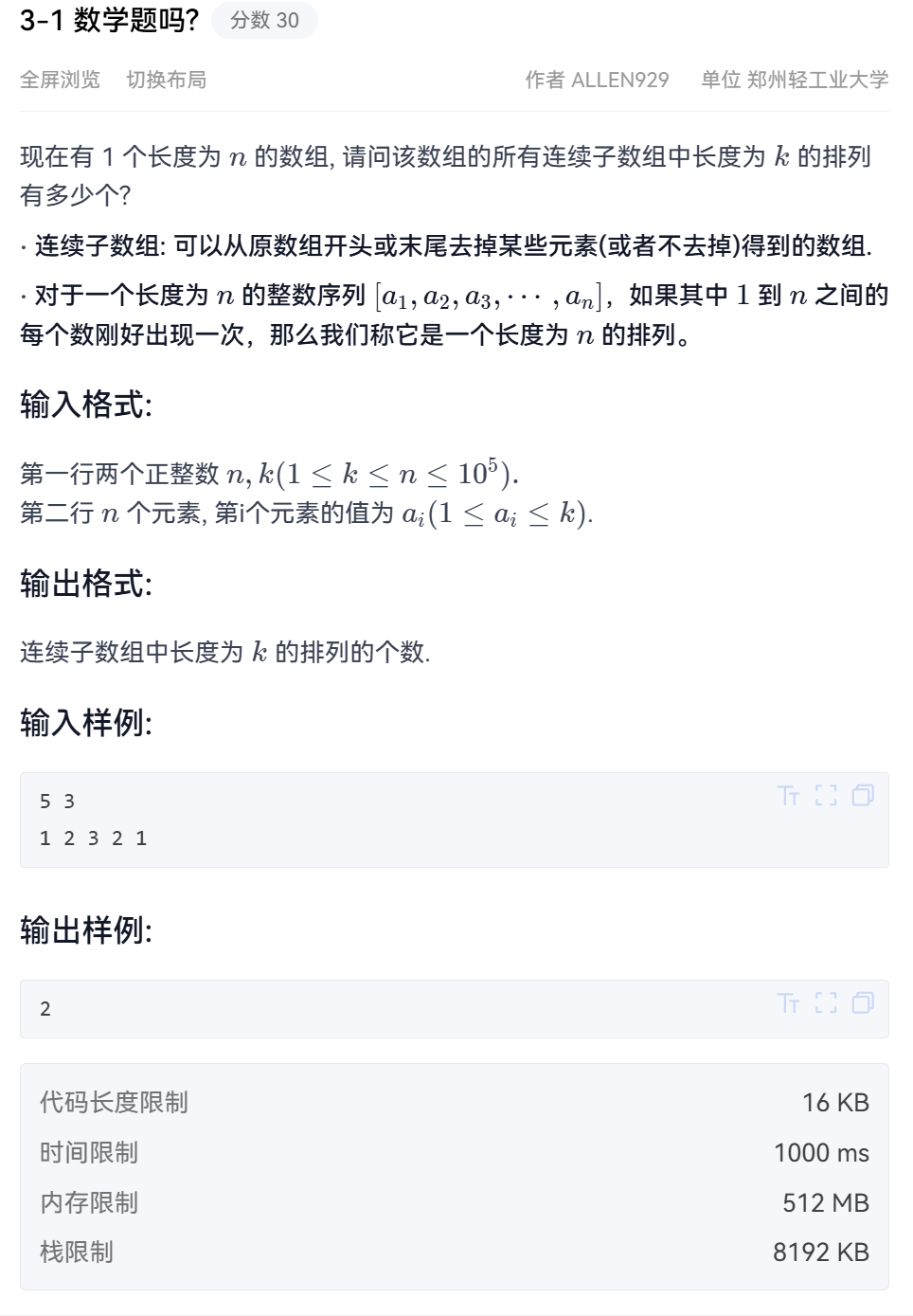
很经典的的一道滑动窗口（双指针），数据范围为10⁵暴力枚举时间复杂度为O(n²)会超时，所以我们用滑动窗口优化

这道题的核心是用滑动窗口（双指针）的方式，高效统计数组中长度恰好为k且元素无重复的连续子数组数量，整体执行逻辑分为初始化 、扩展右边界 、维护无重复窗口 、收缩至目标长度并计数四个关键步骤，具体做法如下：

1. 初始化核心变量

   先定义左指针left、右指针right（初始都指向数组第一个元素），用num记录符合条件的子数组数量，再用哈希表mp实时统计当前窗口内元素的出现次数。。

2. 扩展右边界遍历数组

   用right指针逐个遍历数组元素，每遍历一个元素，就将其加入哈希表并更新出现次数（mp[a[right]]++），这一步的目的是不断扩大窗口范围，纳入新的元素。

3. 维护窗口的无重复特性

   若当前右指针指向的元素在哈希表中的出现次数大于1（说明窗口内该元素重复），则持续将左指针left右移，并把左指针指向的元素从哈希表中计数减1（mp[a[left]]--），直到该重复元素的计数回到1，确保窗口内始终没有重复元素。

4. 收缩窗口至k长度并统计

   计算当前窗口的长度len = right - left + 1，如果窗口长度大于等于k，就继续右移左指针，将窗口收缩到恰好为k的长度；此时窗口满足"长度为k且无重复"的条件，将统计数num加1。

5. 循环推进

   右指针right继续右移，重复上述步骤，直到遍历完整个数组，最终num就是符合条件的子数组数量。

整个过程中，每个元素最多被左、右指针各访问一次，因此能把原本暴力枚举的 O ( n 2 ) O(n^2) O(n2)时间复杂度优化为 O ( n ) O(n) O(n)，实现高效求解。

代码如下：

#include <iostream>
#include <unordered_map>  // 引入哈希表头文件，用于统计窗口内元素出现次数
using namespace std; 
const int N = 1e6 + 10;  // 定义数组最大长度，适配题目大数据量（1e6级别）
int n, k;                // n：数组长度，k：目标子数组的长度
int a[N];                // 存储输入的数组
int main() 
{
    // 输入优化：关闭cin与stdio的同步，解除cin和cout的绑定，加速输入读取
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n >> k;       // 读取数组长度n和目标子数组长度k
    // 循环读取数组元素，数组从1开始索引（符合日常编程习惯）
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
    }

    // 滑动窗口双指针初始化：left左边界、right右边界，初始均指向第一个元素
    int left = 1, right = 1;
    int num = 0;         // 统计符合条件的子数组数量（长度为k且无重复）
    unordered_map<int, int> mp;  // 哈希表：键为数组元素，值为元素在窗口内的出现次数

    // 右指针遍历整个数组，扩展窗口右边界
    while (right <= n)
    {
        mp[a[right]]++;  // 将当前右边界元素加入哈希表，更新出现次数

        // 内层循环：维护窗口无重复特性------若当前右边界元素重复，收缩左边界
        while (mp[a[right]] > 1)
        {
            mp[a[left]]--;  // 左边界元素移出窗口，哈希表计数减1
            left++;         // 左边界右移
        }

        int len = right - left + 1;  // 计算当前窗口的实际长度
        // 若窗口长度≥k，需要收缩至恰好为k的长度
        if (len >= k)
        {
            // 内层循环：将窗口左边界右移，直到窗口长度等于k
            while (len > k)
            {
                mp[a[left]]--;  // 左边界元素移出窗口，哈希表计数减1
                left++;         // 左边界右移
                len = right - left + 1;  // 重新计算窗口长度
            }
            num++;  // 此时窗口满足"长度为k且无重复"，计数加1
        }

        right++;  // 右边界右移，继续遍历下一个元素
    }
    cout << num << '\n';  // 输出符合条件的子数组数量
    return 0;             // 程序正常结束
}

3-2 信号基站的最小干扰中转方案（暴力枚举/数位独立）

这道题我们很容易想到用暴力枚举L~r每个数，我们看数据范围组数t<=10⁴,枚举最多10⁴,最后10⁸可以尝试

1、暴力枚举

// 引入万能头文件，包含C++常用的标准库头文件（如iostream、algorithm等）
#include<bits/stdc++.h>
// 将int类型重定义为long long，避免数值溢出（题目中数值范围可能较大）
#define int long long
// 将endl宏定义为'\n'，减少cout输出时的缓冲区刷新开销，提升输出效率
#define endl '\n'
// 使用std命名空间，避免频繁写std::前缀
using namespace std;
int num; // 全局变量，用于存储每个测试用例中找到的最小相同位总数（干扰度最小值）

// 函数功能：计算两个数字a和b逐位相同的位数（核心逻辑：循环逐位比较）
// 参数：a和b为需要比较的两个数字（题目保证a、b位数相同）
// 返回值：a和b逐位相同的位数
int f(int a, int b)
{
    int cnt = 0; // 统计a和b逐位相同的位数，初始化为0
    while (true) // 无限循环，通过内部break终止
    {
        // 比较a和b的最后一位（个位），若相同则cnt加1
        cnt += (a % 10 == b % 10); 
        // 当a变为个位数时，已完成所有位的比较，终止循环
        if (a <= 9) 
            break; 
        a /= 10; // 去掉a的最后一位（向高位进一位）
        b /= 10; // 去掉b的最后一位（向高位进一位）
    }
    return cnt; // 返回最终统计的相同位数量
}

// 主函数，程序入口（signed main替代main是为了适配long long的重定义，避免链接错误）
signed main()
{
    // 关闭cin与stdio的同步，加速cin输入速度
    ios::sync_with_stdio(0);
    // 解除cin和cout的绑定，进一步提升输入输出效率
    cin.tie(0);
    cout.tie(0);
    
    int t; // 存储测试用例的数量
    cin>>t; // 读取测试用例数量
    // 循环处理每个测试用例
    while(t--)
    {
        int l,r; // l和r分别表示编号的左右边界
        cin>>l>>r; // 读取当前测试用例的l和r
        num=INT_MAX; // 初始化最小相同位总数为int类型的最大值（表示初始时未找到任何值）
        // 遍历[l, r]范围内的所有编号x，寻找最优中转编号
        for(int x=l;x<=r;x++)
        {
            // 计算f(l,x)+f(x,r)（即l到x的相同位数量 + x到r的相同位数量），并更新最小值
            num=min(num,f(l,x)+f(x,r));
            // 剪枝：若找到最小值0（理论上的最小，无法更小），直接终止遍历，减少计算
            if(!num) break;
        }
        cout<<num<<endl; // 输出当前测试用例的最小相同位总数
    }
    return 0; // 程序正常结束
}

---

虽然暴力思路直观，但当 l 和 r 的范围较大（例如 r-l 接近 (10^4)）时，遍历所有数字的次数会显著增加；若测试用例数量达到 (10^4)，整体运算量容易触及时间限制。因此我们需要基于问题的特性，优化计算逻辑。

2、超级优化（数位独立）

• 优化思路：利用"数位独立"直接计算
  观察干扰度的计算规则：f(l,x)+f(x,r) 是每一位贡献的总和 ------对 l 和 r 的某一位数字，x 的该位对总干扰度的贡献仅由这一位的取值决定，与其他位无关。

因此我们可以逐位分析 l 和 r 的对应位 ，直接计算该位的最小贡献，无需枚举所有 x。

过程

用一个标记 found1（初始为 true）表示"是否需要限制 x 的选数范围"，对每一位分场景处理：

1. 若当前位 l[i] == r[i] 且 found1=true ：x 只能选相同数字，该位贡献为 2；
2. 若当前位 r[i]-l[i] == 1 且 found1=true ：x 选 l[i] 或 r[i]，该位贡献为 1，同时将 found1 设为 false（后续位可自由选数，贡献为0）；
3. 若当前位 r[i]-l[i] > 1 ：x 可选中间数，该位贡献为0，直接终止后续计算；
4. 若当前位是 l[i]='9' 且 r[i]='0' ：x 选 9 或 0，该位贡献为 1，同时将 found1 设为 false。

代码如下

#include<iostream>
#define ll long long
#define endl '\n'
using namespace std;

int main()
{
    ll n;
    cin >> n;
    while (n--) // 处理n组测试用例
    {
        string a, b;
        cin >> a >> b;
        bool found1 = true; // 标记是否需限制选数范围
        ll l = a.size(); // a/b的长度（位数相同）
        ll count = 0; // 累加最小冗余度
        for (ll i = 0; i < l; i++) // 逐位分析
        {
            if (b[i] == a[i] && found1) 
            {
                count += 2; // 位相同，只能选该数，贡献2
            } 
            else if ((b[i] - a[i]) == 1 && found1) 
            {
                count++;
                found1 = false; // 位差1，贡献1，后续位可自由选
            } 
            else if ((b[i] - a[i]) > 1)
            {
                break; // 位差>1，后续贡献0，终止计算
            } 
            else if (b[i] == '0' && a[i] == '9')
            {
                count++;
                found1 = false; // 9/0循环，贡献1，后续位可自由选
            } 
            else 
            {
                count += 0; // 其他情况，贡献0
            }
        }
        cout << count << endl; // 输出最小冗余度
    }
    return 0;
}

代码说明

• 用字符串存储 l 和 r，方便逐位访问；
• found1 标记范围限制状态，一旦解除，后续位无需计算；
• 逐位处理后直接累加最小贡献，最终输出总和。

通过"数位独立"的特性，我们将遍历所有 x 的暴力逻辑，优化为逐位计算最小贡献，时间复杂度降至 (O(位数))（最多5位），既能保证正确性，又能高效通过所有测试用例。

3-3 链表奇偶拆分（模拟）

这道题就是简单的模拟题，按照题目要求就行

代码如下

#include<iostream>
#include<vector>
using namespace std;

const int N = 1e6 + 7;  // 数组最大容量，适配链表节点地址范围
// 链表节点结构体：模拟单链表节点
typedef struct
{
	int key;    // 节点地址（作为数组下标）
	int k;      // 节点存储的数据
	int next;   // 下一个节点的地址（-1表示尾节点）
}ST;

ST arr[N];  // 数组模拟链表：以节点地址为下标，快速查找节点

int main()
{
	int cur, n;
	cin >> cur >> n;  // cur-链表头节点地址，n-输入的节点总数
	int key1, k1, next1;

	// 1. 读取所有节点，按地址存入数组（数组下标=节点地址）
	for (int i = 0; i < n; i++)
	{
		cin >> key1 >> k1 >> next1;  // 读取节点地址、数据、下一个地址
		arr[key1].key = key1;        // 记录节点地址
		arr[key1].k = k1;            // 记录节点数据
		arr[key1].next = next1;      // 记录下一个节点地址
	}

	vector<ST>brr, crr;  // brr-存奇数位置节点（第2、4、6...位），crr-存偶数位置节点（第1、3、5...位）
	int pos = 0;         // 记录当前节点的位置（从0开始计数）

	// 2. 遍历链表，按位置奇偶拆分节点（终止条件：当前节点地址为-1）
	while (cur != -1)
	{
		if (pos % 2 != 0)  // 位置1、3、5...（第2、4、6...个节点）→ 存入brr
		{
			brr.push_back({ arr[cur].key, arr[cur].k, arr[cur].next });
		}
		else  // 位置0、2、4...（第1、3、5...个节点）→ 存入crr
		{
			crr.push_back({ arr[cur].key, arr[cur].k, arr[cur].next });
		}
		cur = arr[cur].next;  // 移动到下一个节点
		pos++;                // 节点位置计数+1
	}

	// 3. 输出偶数位置节点链表（crr）
	int len1 = crr.size();  // crr的节点数
	for (int i = 0; i < len1; i++)
	{
		printf("%05d %d ", crr[i].key, crr[i].k);  // 输出节点地址（补0到5位）、数据
		if (i != len1 - 1)  // 非最后一个节点，输出下一个节点地址（补0到5位）
		{
			printf("%05d\n", crr[i+1].key);
		}
		else  // 最后一个节点，下一个地址为-1
		{
			cout << -1 << '\n';
		}
	}

	// 4. 输出奇数位置节点链表（brr）
	int len2 = brr.size();  // brr的节点数
	for (int i = 0; i < len2; i++)
	{
		printf("%05d %d ", brr[i].key, brr[i].k);  // 输出节点地址（补0到5位）、数据
		if (i != len2 - 1)  // 非最后一个节点，输出下一个节点地址（补0到5位）
		{
			printf("%05d\n", brr[i+1].key);
		}
		else  // 最后一个节点，下一个地址为-1
		{
			cout << -1 << '\n';
		}
	}
	return 0;
}

总结

总体来说，本次天梯赛难度不难，许多题甚至暴力就可以解，但很有实际意义，也是一次考察自己代码能力的机会，博主会持续分享的，感谢大家的支持啦！