深入浅出蓝桥杯：算法基础概念与实战应用（二）基础算法(下)

铭哥的编程日记2025-11-16 0:02

算法基础概念与实战应用（二） 基础算法(下)

文章目录

  • [算法基础概念与实战应用（二） 基础算法(下)](#算法基础概念与实战应用（二） 基础算法(下))
  • 一、贪心算法
  • [8.1 简单贪⼼](#8.1 简单贪⼼)
    • [8.1.1 货仓选址](#8.1.1 货仓选址)
    • [8.1.2 最⼤⼦段和](#8.1.2 最⼤⼦段和)
    • [8.1.3 纪念品分组](#8.1.3 纪念品分组)
    • [8.1.4 排座椅](#8.1.4 排座椅)
    • [8.1.5 矩阵消除游戏](#8.1.5 矩阵消除游戏)
  • [8.2 推公式](#8.2 推公式)
    • [8.2.1 拼数](#8.2.1 拼数)
    • [8.2.2 保卫花园](#8.2.2 保卫花园)
    • [8.2.3 奶⽜玩杂技](#8.2.3 奶⽜玩杂技)
  • [8.3 哈夫曼编码](#8.3 哈夫曼编码)
    • [8.3.1 哈夫曼编码](#8.3.1 哈夫曼编码)
    • [8.3.2 合并果⼦](#8.3.2 合并果⼦)
  • [8.4 区间问题](#8.4 区间问题)
    • [8.4.1 线段覆盖](#8.4.1 线段覆盖)
    • [8.4.2 Radar Installation](#8.4.2 Radar Installation)
    • [8.4.3 Sunscreen](#8.4.3 Sunscreen)
    • [8.4.4 ⽜栏预定](#8.4.4 ⽜栏预定)
  • [9. 倍增思想](#9. 倍增思想)
    • [9.1 快速幂](#9.1 快速幂)
    • [9.2 ⼤整数乘法](#9.2 ⼤整数乘法)
  • [10. 离散化](#10. 离散化)
  • [11. 递归初阶](#11. 递归初阶)
  • 总结

一、贪心算法

8.1 简单贪⼼

8.1.1 货仓选址

牛客网链接

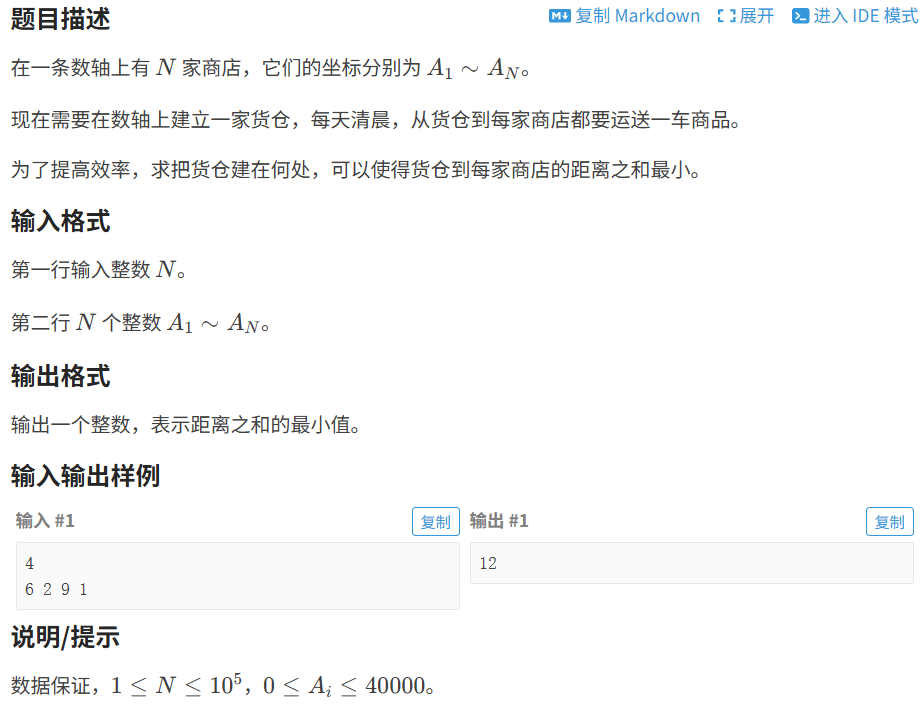
代码如下（示例）：

c 复制代码 
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int n;
LL a[N];
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	sort(a + 1, a + 1 + n);
	LL ret = 0;
	// 利⽤中间值来计算
	// for(int i = 1; i <= n; i++)
	// {
	// ret += abs(a[i] - a[n / 2]);
	// }
	// ⽤结论计算
	for (int i = 1; i <= n / 2; i++)
	{
		ret += a[n - i + 1] - a[i];
	}
	cout << ret << endl;
	return 0;
}

8.1.2 最⼤⼦段和

牛客网链接


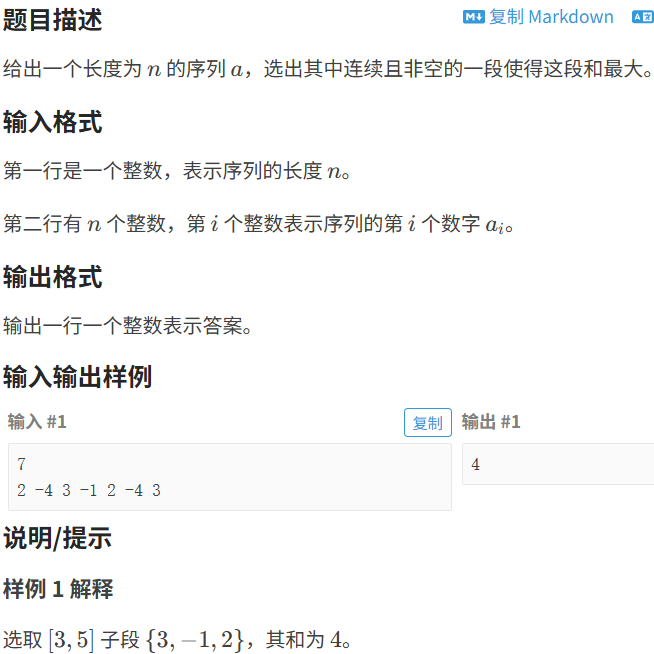
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 2e5 + 10;
int n;
LL a[N];
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	LL sum = 0, ret = -1e6;
	for (int i = 1; i <= n; i++)
	{
		sum += a[i];
		ret = max(ret, sum);
		if (sum < 0) sum = 0;
	}
	cout << ret << endl;
	return 0;
}

8.1.3 纪念品分组

牛客网链接


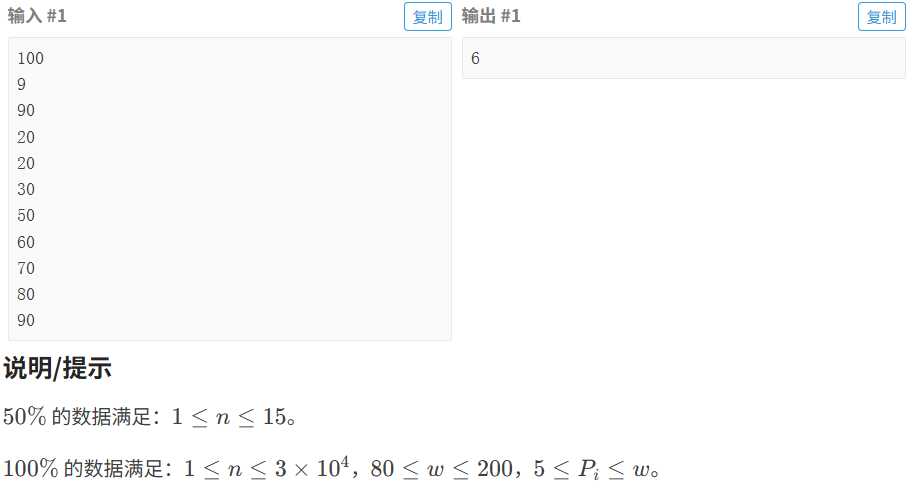
代码如下（示例）：

c 复制代码 
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 3e4 + 10;
int w, n;
int a[N];
int main()
{
	cin >> w >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	sort(a + 1, a + 1 + n);
	int l = 1, r = n, ret = 0;
	while (l <= r)
	{
		if (a[l] + a[r] <= w) l++, r--;
		else r--;
		ret++;
	}
	cout << ret << endl;
	return 0;
}

8.1.4 排座椅

牛客网链接


代码如下（示例）：

c 复制代码 
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
struct node
{
	int index;
	int cnt;
}row[N], col[N];
int m, n, k, l, d;
// 按照 cnt 从⼤到⼩排序
bool cmp1(node& x, node& y)
{
	return x.cnt > y.cnt;
}
// 按照 index 从⼩到⼤排序
bool cmp2(node& x, node& y)
{
	return x.index < y.index;
}
int main()
{
	cin >> m >> n >> k >> l >> d;
	// 初始化结构体数组
	for (int i = 1; i <= m; i++) row[i].index = i;
	for (int i = 1; i <= n; i++) col[i].index = i;
	while (d--)
	{
		int x, y, p, q; cin >> x >> y >> p >> q;
		if (x == p) col[min(y, q)].cnt++;
		else row[min(x, p)].cnt++;
	}
	// 对两个数组按照 cnt 从⼤到⼩排序
	sort(row + 1, row + 1 + m, cmp1);
	sort(col + 1, col + 1 + n, cmp1);
	// 对 row 数组，前 k 个元素，按照下标从⼩到⼤排序
	sort(row + 1, row + 1 + k, cmp2);
	// 对 col 数组，前 l 个元素，按照下标从⼩到⼤排序
	sort(col + 1, col + 1 + l, cmp2);
	for (int i = 1; i <= k; i++)
	{
		cout << row[i].index << " ";
	}
	cout << endl;
	for (int i = 1; i <= l; i++)
	{
		cout << col[i].index << " ";
	}
	cout << endl;
	return 0;
}

8.1.5 矩阵消除游戏

牛客网链接

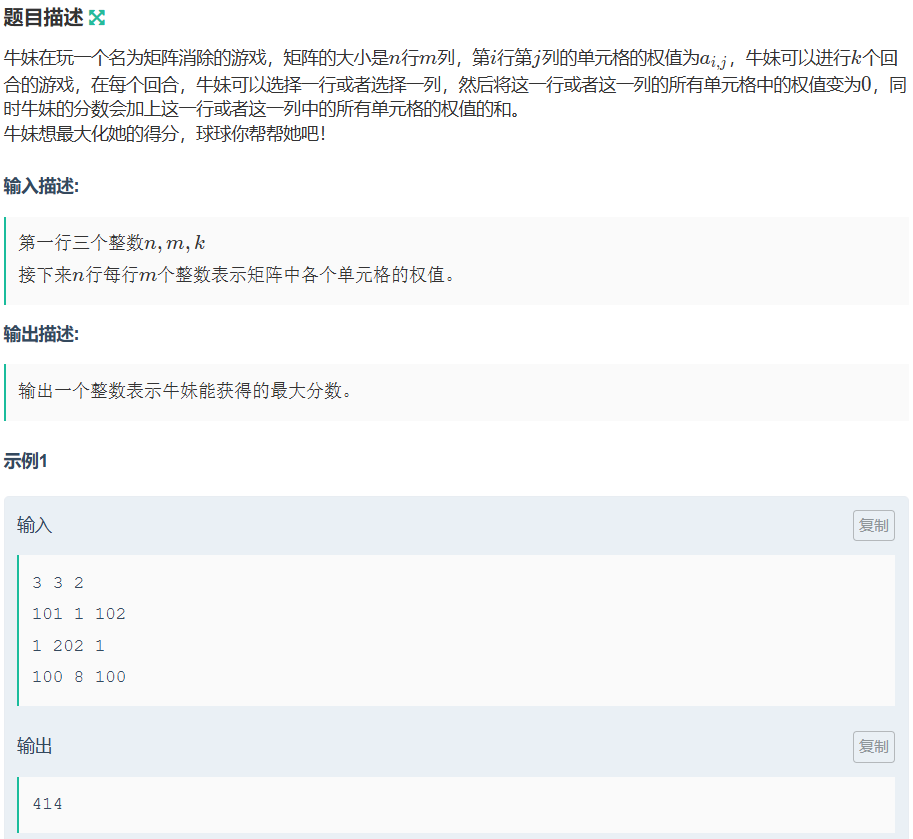
代码如下（示例）：

c 复制代码 
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 20;
int n, m, k;
int a[N][N];
int col[N]; // 统计列和
// 统计 x 的⼆进制表⽰中 1 的个数
int calc(int x)
{
	int ret = 0;
	while (x)
	{
		ret++;
		x -= x & -x;
	}
	return ret;
}
// 按照值从⼤到⼩排序
bool cmp(int a, int b)
{
	return a > b;
}
int main()
{
	cin >> n >> m >> k;
	for (int i = 0; i < n; i++)
		for (int j = 0; j < m; j++)
			cin >> a[i][j];
	int ret = 0;
	// 暴⼒枚举出⾏的所有选法
	for (int st = 0; st < (1 << n); st++)
	{
		int cnt = calc(st);
		if (cnt > k) continue; // 不合法的状态
		memset(col, 0, sizeof col);
		int sum = 0; // 记录当前选法中的和
		for (int i = 0; i < n; i++)
		{
			for (int j = 0; j < m; j++)
			{
				if ((st >> i) & 1) sum += a[i][j];
				else col[j] += a[i][j];
			}
		}
		// 处理列
		sort(col, col + m, cmp);
		// 选 k - cnt 列
		for (int i = 0; i < k - cnt; i++) sum += col[i];
		ret = max(ret, sum);
	}
	cout << ret << endl;
	return 0;
}

8.2 推公式

8.2.1 拼数

洛谷链接

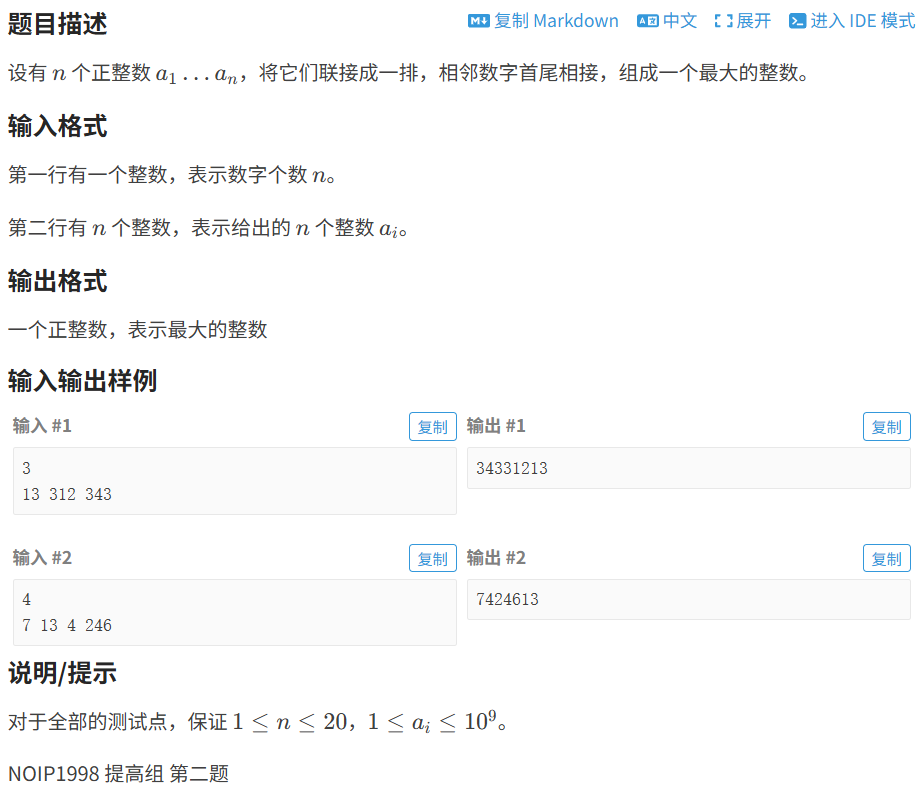
代码如下（示例）：

c 复制代码 
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 25;
int n;
string a[N];
bool cmp(string& x, string& y)
{
	return x + y > y + x;
}
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	// 排序
	sort(a + 1, a + 1 + n, cmp);
	for (int i = 1; i <= n; i++) cout << a[i];
	return 0;
}

8.2.2 保卫花园

洛谷链接

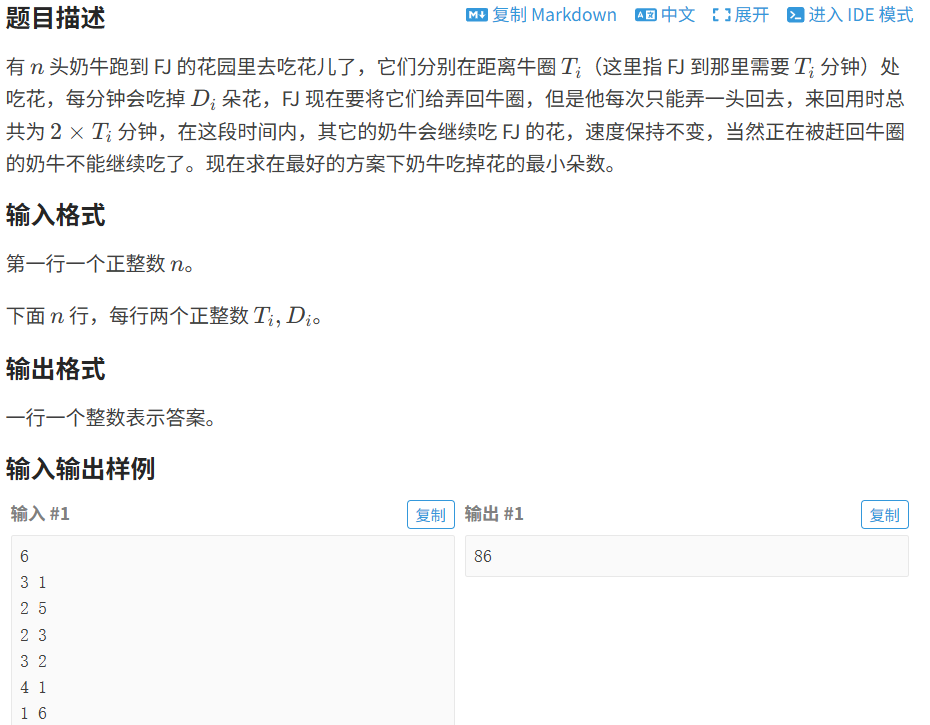
代码如下（示例）：

c 复制代码 
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int n;
struct node
{
	int t;
	int d;
}a[N];
bool cmp(node& x, node& y)
{
	return x.t * y.d < y.t* x.d;
}
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i].t >> a[i].d;
	}
	sort(a + 1, a + 1 + n, cmp);
	LL ret = 0, t = 0;
	for (int i = 1; i <= n; i++)
	{
		ret += a[i].d * t;
		t += 2 * a[i].t;
	}
	cout << ret << endl;
	return 0;
}

8.2.3 奶⽜玩杂技

洛谷链接


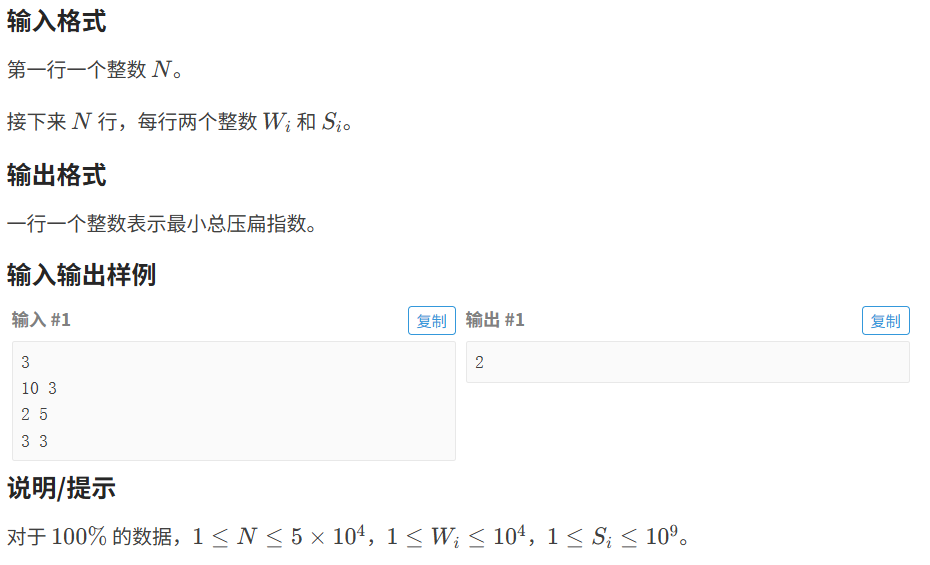
代码如下（示例）：

c 复制代码 
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 5e4 + 10;
int n;
struct node
{
	int w, s;
}a[N];
bool cmp(node& i, node& j)
{
	return i.w + i.s < j.w + j.s;
}
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i].w >> a[i].s;
	sort(a + 1, a + 1 + n, cmp);
	LL ret = -1e9 - 10, w = 0;
	for (int i = 1; i <= n; i++)
	{
		ret = max(ret, w - a[i].s);
		w += a[i].w;
	}
	cout << ret << endl;
	return 0;
}

8.3 哈夫曼编码

8.3.1 哈夫曼编码

洛谷链接

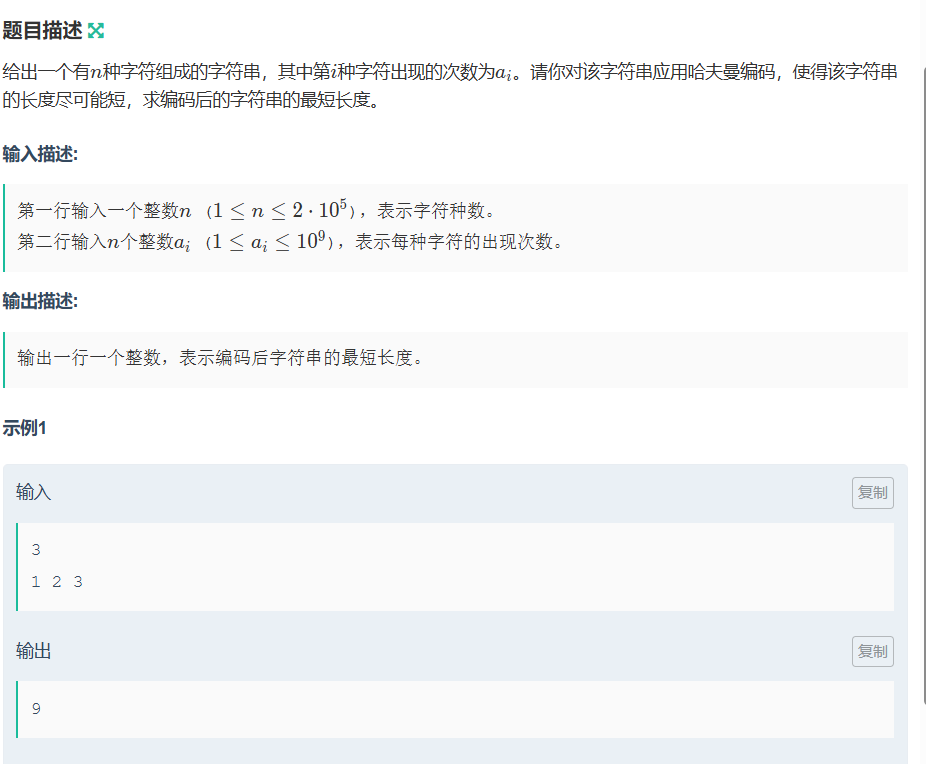
代码如下（示例）：

c 复制代码 
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
typedef long long LL;
const int N = 2e5 + 10;
int n;
priority_queue<LL, vector<LL>, greater<LL>> heap; // ⼩根堆
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		LL x; cin >> x;
		heap.push(x);
	}
	LL len = 0;
	while (heap.size() > 1)
	{
		// 每次拿出权值最⼩的两棵树合并
		LL x = heap.top(); heap.pop();
		LL y = heap.top(); heap.pop();
		LL t = x + y;
		len += t;
		heap.push(t);
	}
	cout << len << endl;
	return 0;
}

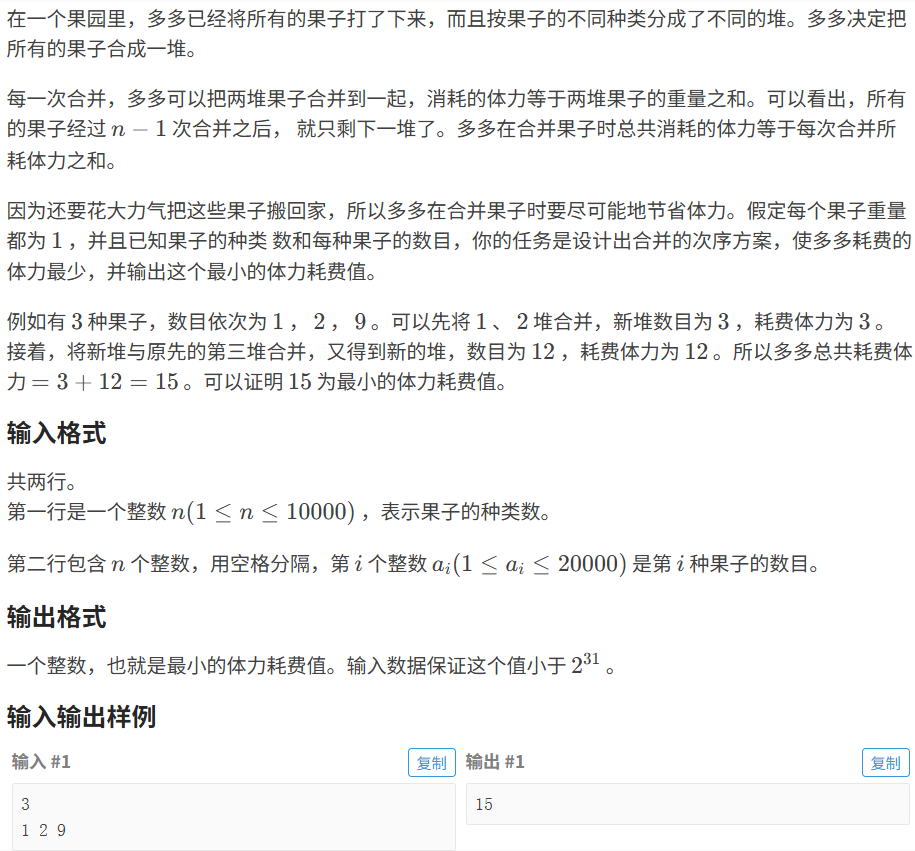
8.3.2 合并果⼦

洛谷链接

代码如下（示例）：

c 复制代码 
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
typedef long long LL;
int n;
priority_queue<LL, vector<LL>, greater<LL>> heap;
int main()
{
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		LL x;
		cin >> x;
		heap.push(x);
	}
	LL sum = 0;
	while (heap.size() > 1)
	{
		// 取出最⼩的两堆合并
		LL a = heap.top(); heap.pop();
		LL b = heap.top(); heap.pop();
		heap.push(a + b);
		sum += a + b;
	}
	cout << sum << endl;
	return 0;
}

8.4 区间问题

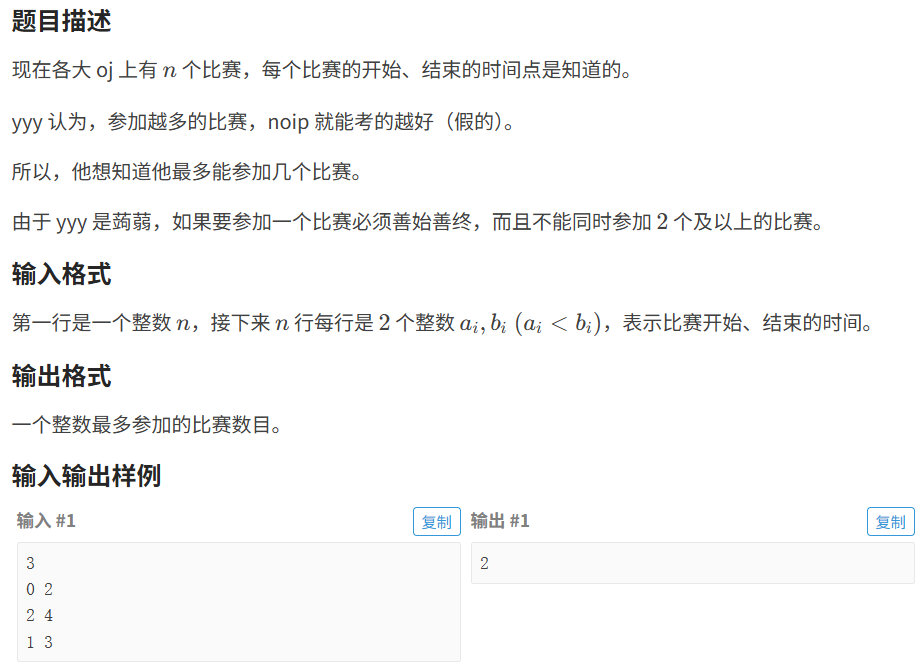
8.4.1 线段覆盖

洛谷链接

代码如下（示例）：

c 复制代码 
#include <iostream>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e6 + 10;
int n;
PII a[N];
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i].first >> a[i].second;
	sort(a + 1, a + 1 + n); // 默然按照⾸元素⽐较
	int r = a[1].second, ret = 1;
	for (int i = 2; i <= n; i++)
	{
		int x = a[i].first, y = a[i].second;
		if (r <= x) // 没有重叠
		{
			ret++;
			r = y;
		}
		else // 有重叠，就选右边界最⼩的那⼀个
		{
			r = min(r, y);
		}
	}
	cout << ret << endl;
	return 0;
}

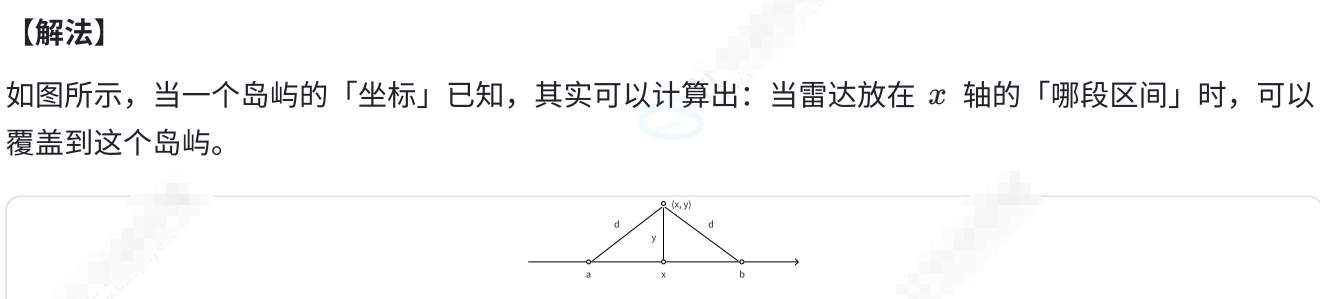
8.4.2 Radar Installation

洛谷链接



代码如下（示例）：

c 复制代码 
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, d;
struct node
{
	double l, r;
}a[N];
bool cmp(node& x, node& y)
{
	return x.l < y.l;
}
int main()
{
	int cnt = 0;
	while (cin >> n >> d, n && d)
	{
		cnt++;
		bool flag = false; // 有可能岛屿太远，⽆论如何也覆盖不到
		for (int i = 1; i <= n; i++)
		{
			double x, y; cin >> x >> y;
			if (y > d) flag = true;
			else
			{
				double t = sqrt(d * d - y * y);
				a[i].l = x - t, a[i].r = x + t;
			}
		}
		cout << "Case " << cnt << ": ";
		if (flag) cout << -1 << endl;
		else
		{
			sort(a + 1, a + 1 + n, cmp);
			int ret = 1;
			double r = a[1].r;
			for (int i = 2; i <= n; i++)
			{
				double x = a[i].l, y = a[i].r;
				if (x > r) // 没有重叠
				{
					ret++;
					r = y;
				}
				else // 有重叠
				{
					r = min(r, y);
				}
			}
			cout << ret << endl;
		}
	}
	return 0;
}

8.4.3 Sunscreen

洛谷链接


代码如下（示例）：

c 复制代码 
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 2510;
int n, m;
struct node
{
	int x, y;
}a[N], b[N];
bool cmp1(node& x, node& y)
{
	return x.y < y.y;
}
bool cmp2(node& x, node& y)
{
	return x.x < y.x;
}
bool cmp3(node & x, node & y)
{
	return x.x > y.x;
}
// 所有区间按照右端点从⼩到⼤排序
// 所有点按照从⼩到⼤排序
void solve1()
{
	sort(a + 1, a + 1 + n, cmp1);
	sort(b + 1, b + 1 + m, cmp2);
	int ret = 0;
	for (int i = 1; i <= n; i++)
	{
		int l = a[i].x, r = a[i].y;
		for (int j = 1; j <= m; j++)
		{
			// 选⼀个最⼩的，符合要求的点
			int& sp = b[j].x, & cnt = b[j].y;
			if (!cnt || sp < l) continue;
			if (sp > r) break;
			cnt--;
			ret++;
			break;
		}
	}
	cout << ret << endl;
}
// 所有区间按照左端点从⼤到⼩排列
// 所有点从⼤到⼩排列
void solve2()
{
	sort(a + 1, a + 1 + n, cmp3);
	sort(b + 1, b + 1 + m, cmp3);
	int ret = 0;
	for (int i = 1; i <= n; i++)
	{
		int l = a[i].x, r = a[i].y;
		for (int j = 1; j <= m; j++)
		{
			// 选⼀个最⼤的，符合要求的点
			int& sp = b[j].x, & cnt = b[j].y;
			if (!cnt || sp > r) continue;
			if (sp < l) break;
			ret++;
			cnt--;
			break;
		}
	}
	cout << ret << endl;
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++) cin >> a[i].x >> a[i].y;
	for (int i = 1; i <= m; i++) cin >> b[i].x >> b[i].y;
	// solve1(); // 按照右端点排序
	solve2(); // 按照左端点排序
}

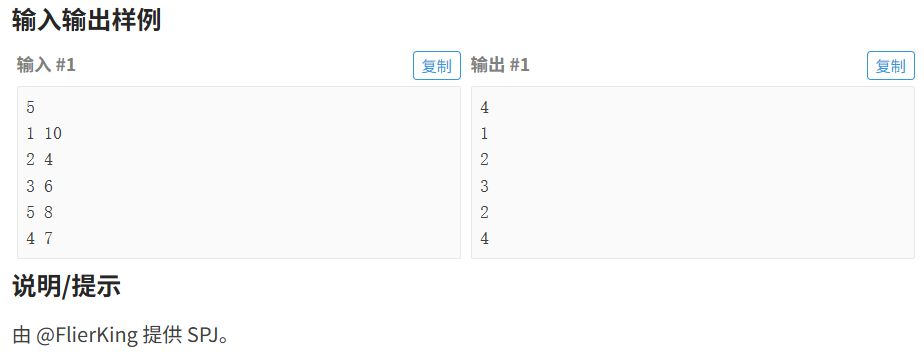
8.4.4 ⽜栏预定

洛谷链接



代码如下（示例）：

c 复制代码 
#include <iostream>
#include <map>
#include <algorithm>
using namespace std;
const int N = 5e4 + 10;
int n;
struct node
{
	// 存每⼀头⽜的信息：开始时间，结束时间，排序之前的位置，分配的⽜棚号
	int x, y, pos, num;
}a[N];
int cnt;
int ret[N];
multimap<int, int> st;
bool cmp(node& x, node& y)
{
	return x.x < y.x;
}
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i].x >> a[i].y;
		a[i].pos = i;
	}
	sort(a + 1, a + 1 + n, cmp);
	for (int i = 1; i <= n; i++)
	{
		int l = a[i].x, r = a[i].y;
		auto it = st.upper_bound(l);
		// 不能接在任何⼀个区间后⾯，那就新开⼀个区间
		if (it == st.end())
		{
			st.insert({ r, ++cnt });
			a[i].num = cnt;
		}
		else // 能接在某个区间后⾯，那就接上去
		{
			int p = it->second;
			st.erase(it); // 把之前⽜删掉
			st.insert({ r, p }); // 新来的⽜放进去
			a[i].num = p;
		}
	}
	cout << cnt << endl;
	for (int i = 1; i <= n; i++)
	{
		ret[a[i].pos] = a[i].num;
	}
	for (int i = 1; i <= n; i++) cout << ret[i] << endl;
	return 0;
}

9. 倍增思想

9.1 快速幂

洛谷链接


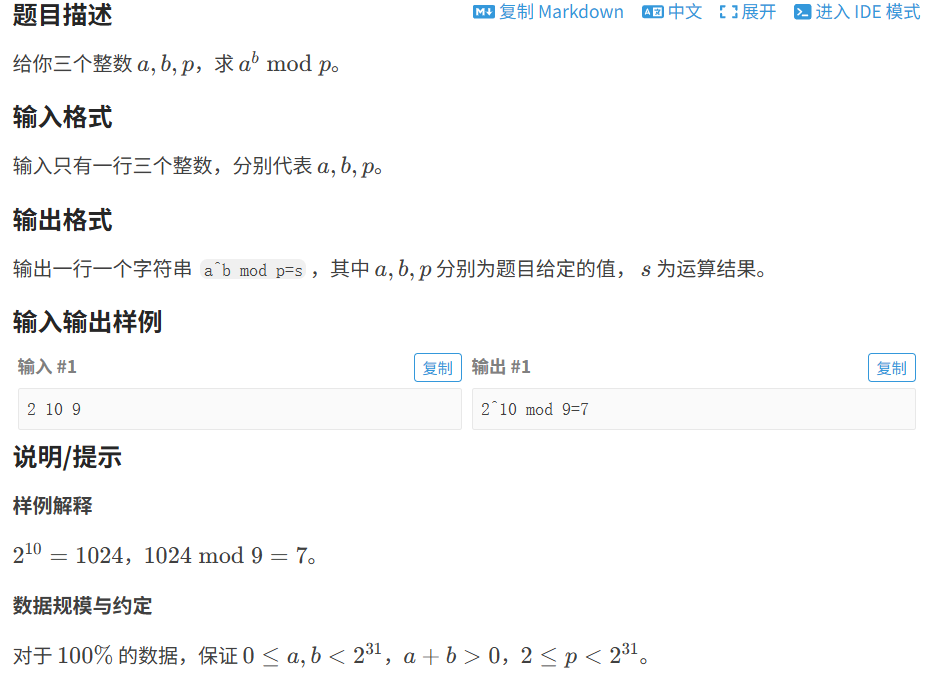
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
typedef long long LL;
// a^b % p 的值
LL quickpow(LL a, LL b, LL p)
{
	LL ret = 1;
	while (b)
	{
		if (b & 1) ret = ret * a % p;
		a = a * a % p;
		b >>= 1; // 提取 b 的⼆进制位
	}
	return ret;
}
int main()
{
	LL a, b, p;
	scanf("%lld%lld%lld", &a, &b, &p);
	printf("%lld^%lld mod %lld=%lld\n", a, b, p, quickpow(a, b, p));
	return 0;
}

9.2 ⼤整数乘法

洛谷链接

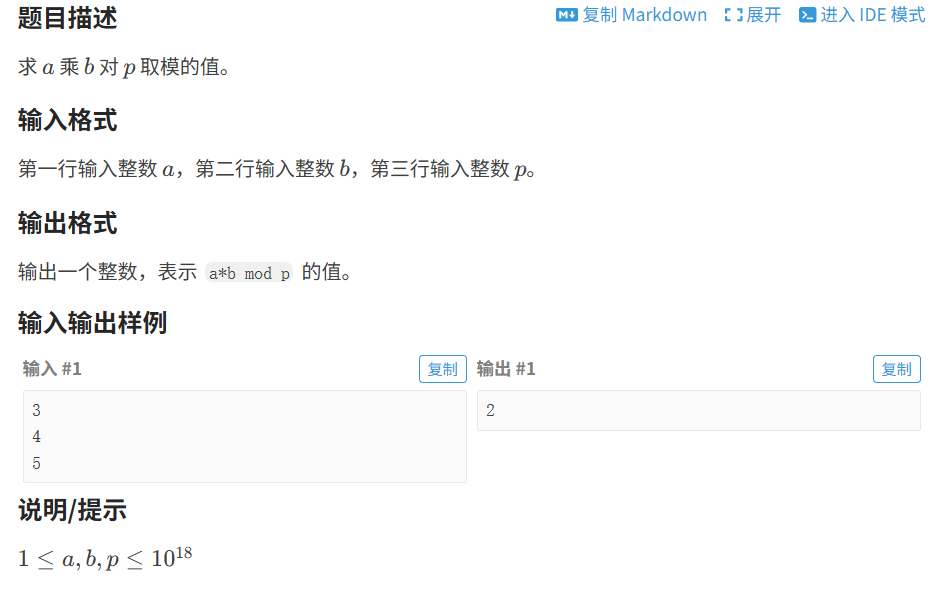
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
typedef long long LL;
// 加法⽐乘法快，⽽且防溢出
LL qmul(LL a, LL b, LL p)
{
	LL sum = 0;
	while (b) // 枚举 b 的⼆进制位
	{
		if (b & 1) sum = (sum + a) % p;
		a = (a + a) % p; // 计算下⼀个权值
		b >>= 1;
	}
	return sum % p;
}
int main()
{
	LL a, b, p;
	cin >> a >> b >> p;
	cout << qmul(a % p, b, p) << endl;
	return 0;
}

10. 离散化

模板一：

代码如下（示例）：

c 复制代码 
// 离散化⽅式⼀：排序 + 去重 + ⼆分查找离散化后的值
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int n;
int a[N]; // 原始数据
int pos; // 记录离散化数组中元素的个数
int disc[N]; // 离散化需要的数组
// ⼆分查找离散化之后的值，其实就是排序之后的下标
int find(int x)
{
	int l = 1, r = pos; // 注意查找的区间
	while (l < r)
	{
		int mid = (l + r) >> 1;
		if (disc[mid] >= x) r = mid;
		else l = mid + 1;
	}
	return l;
}
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		int x; cin >> x;
		a[i] = x;
		disc[++pos] = x; // 数据放进离散化数组中
	}
	// 离散化：排序 + 去重
	sort(disc + 1, disc + 1 + pos);
	pos = unique(disc + 1, disc + 1 + pos) - (disc + 1);
	// 找到离散化之后的值
	for (int i = 1; i <= n; i++)
	{
		int x = a[i];
		cout << x << "离散化之后是： " << find(x) << endl; // ⼆分查找离散化之后的值
	}
}

模板二：

代码如下（示例）：

c 复制代码 
// 离散化⽅式⼆：排序 + STL
// 本质是和⽅式⼀ 样的，只不过借助了 STL，去重以及查找更⽅便
#include <iostream>
#include <unordered_map>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int n;
int a[N]; // 原始数据
int tmp[N]; // ⽤来排序的数组
int cnt;
unordered_map<int, int> id; // 记录离散化之后的值
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		int x; cin >> x;
		a[i] = x;
		tmp[i] = x; // 数据放进离散化数组中
	}
	// 离散化：排序 + 放进哈希表中
	sort(tmp + 1, tmp + 1 + n);
	for (int i = 1; i <= n; i++)
	{
		if (id.count(tmp[i])) continue; // 如果已经存过这个数，不做处理
		cnt++; // 这个数映射之后的值
		id[tmp[i]] = cnt; // 放进哈希表中
	}
	// 找到离散化之后的值
	for (int i = 1; i <= n; i++)
	{
		int x = a[i];
		cout << x << "离散化之后是： " << id[a[i]] << endl; // ⼆分查找离散化之后的值
	}
	return 0;
}

10.1 火烧赤壁

洛谷链接


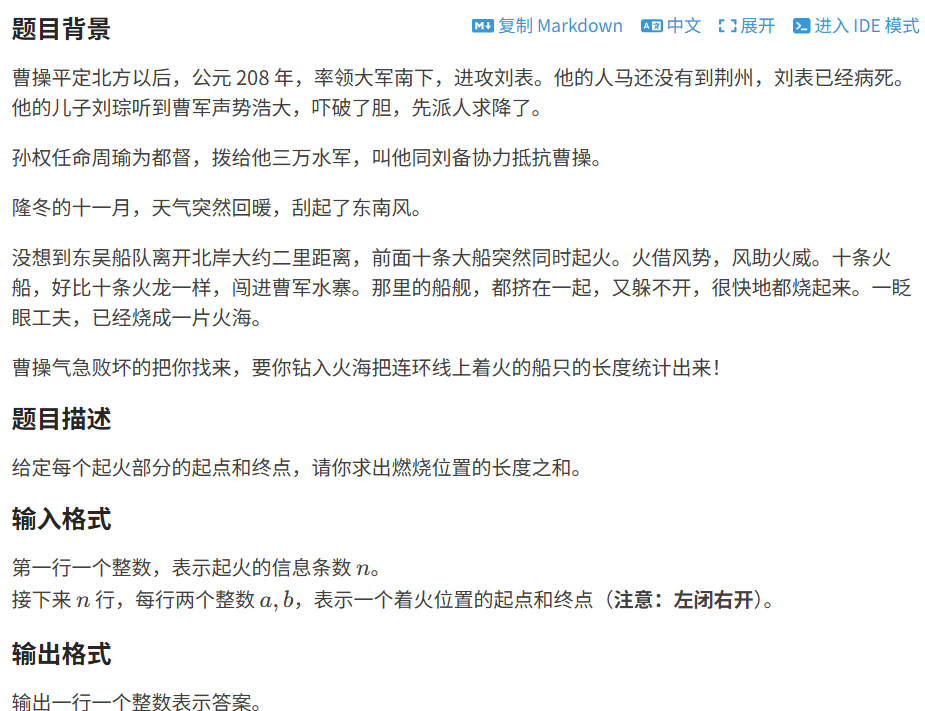
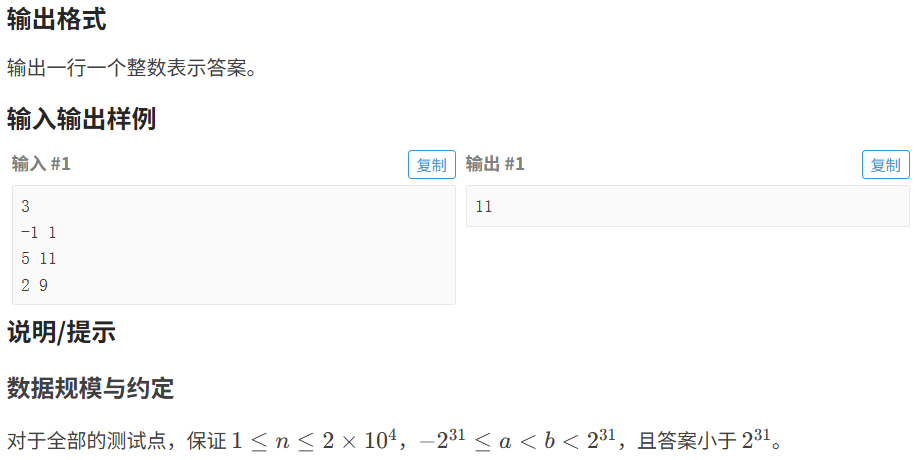
代码如下（示例）：

c 复制代码 
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 2e4 + 10;
int n;
int l[N], r[N];
int m; // 离散数组的⼤⼩
int disc[N * 2]; // 离散之后的数组
int f[N * 2]; // 差分数组
int find(int x)
{
	int l = 1, r = m;
	while (l < r)
	{
		int mid = (l + r + 1) >> 1;
		if (disc[mid] <= x) l = mid;
		else r = mid - 1;
	}
	return l;
}
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		int x, y; cin >> x >> y;
		l[i] = x, r[i] = y;
		disc[++m] = l[i], disc[++m] = r[i];
	}
	// 离散化处理
	sort(disc + 1, disc + 1 + m);
	m = unique(disc + 1, disc + 1 + m) - disc - 1;
	// 处理区间修改
	for (int i = 1; i <= n; i++)
	{
		int x = find(l[i]), y = find(r[i]);
		f[x] += 1, f[y] -= 1;
	}
	// 还原数组
	for (int i = 1; i <= m; i++) f[i] += f[i - 1];
	// 找出每⼀段⼤于0的区间，统计⻓度
	int sum = 0;
	for (int i = 1; i <= m; i++)
	{
		if (f[i] <= 0) continue;
		int j = i;
		while (j <= m && f[j] > 0) j++;
		// 累加⻓度的时候记得使⽤离散化之前的值
		sum += disc[j] - disc[i];
		i = j;
	}
	cout << sum << endl;
	return 0;
}

10.2 贴海报

洛谷链接




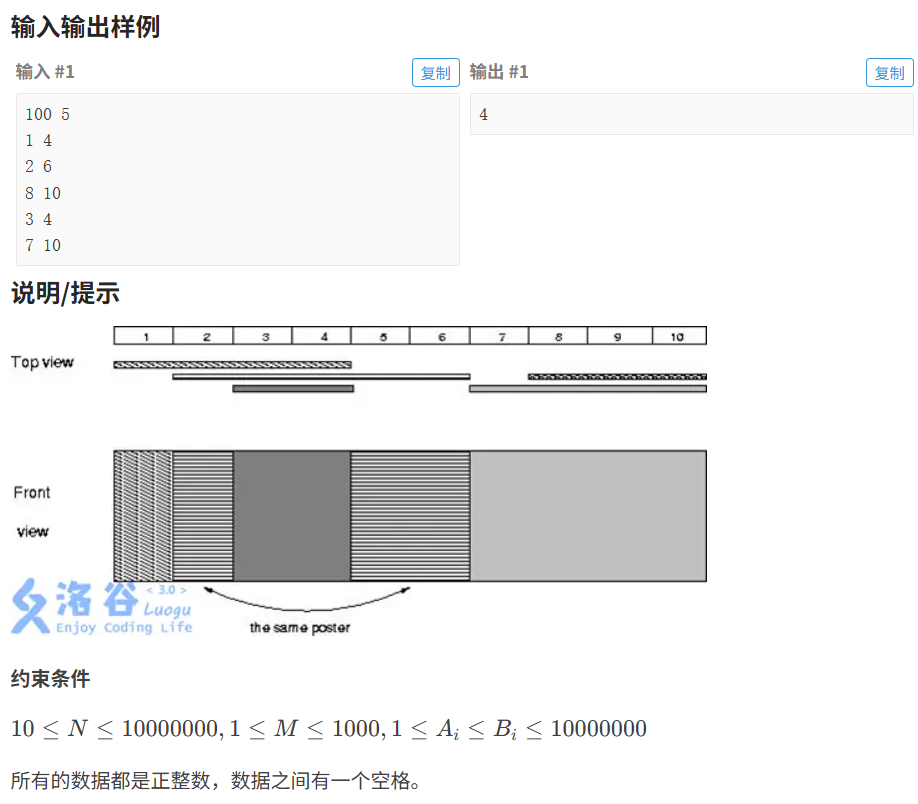
代码如下（示例）：

c 复制代码 
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int a[N], b[N];
int pos;
int disc[N * 4]; // 因为有两套位置
int w[N * 4];
bool mp[N];
// 找到 x 映射之后的数，也就是 x 的下标
int find(int x)
{
	int l = 1, r = pos;
	while (l < r)
	{
		int mid = (l + r) >> 1;
		if (disc[mid] >= x) r = mid;
		else l = mid + 1;
	}
	return l;
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= m; i++)
	{
		int x, y; cin >> x >> y;
		a[i] = x, b[i] = y;
		// 离散化之后有可能导致区间缩⼩，多加⼀个位置
		disc[++pos] = x, disc[++pos] = x + 1;
		disc[++pos] = y, disc[++pos] = y + 1;
	}
	// 离散化
	sort(disc + 1, disc + 1 + pos);
	pos = unique(disc + 1, disc + 1 + pos) - (disc + 1);
	// ⽤离散化之后的值覆盖区间
	for (int i = 1; i <= m; i++)
	{
		int x = find(a[i]), y = find(b[i]);
		for (int j = x; j <= y; j++) w[j] = i;
	}
	// 统计整个数组中，⼀共有多少个不同的数
	int cnt = 0;
	for (int i = 1; i <= pos; i++)
	{
		int x = w[i];
		if (!x) continue; // 不要统计 0
		if (mp[x]) continue;
		cnt++;
		mp[x] = true;
	}
	cout << cnt << endl;
	return 0;
}

11. 递归初阶

总结

相关推荐
Swift社区1 小时前
LeetCode 421 - 数组中两个数的最大异或值
算法·leetcode·职场和发展
cici158741 小时前
基于高光谱成像和偏最小二乘法（PLS）的苹果糖度检测MATLAB实现
算法·matlab·最小二乘法
StarPrayers.3 小时前
自蒸馏学习方法
人工智能·算法·学习方法
大锦终3 小时前
【动规】背包问题
c++·算法·动态规划
智者知已应修善业3 小时前
【c语言蓝桥杯计算卡片题】2023-2-12
c语言·c++·经验分享·笔记·算法·蓝桥杯
hansang_IR4 小时前
【题解】洛谷 P2330 [SCOI2005] 繁忙的都市 [生成树]
c++·算法·最小生成树
Croa-vo4 小时前
PayPal OA 全流程复盘｜题型体验 + 成绩反馈 + 通关经验
数据结构·经验分享·算法·面试·职场和发展
AndrewHZ4 小时前
【图像处理基石】 怎么让图片变成波普风？
图像处理·算法·计算机视觉·风格迁移·cv
无极小卒4 小时前
如何在三维空间中生成任意方向的矩形内部点位坐标
开发语言·算法·c#
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03BongoCat - 跨平台键盘猫动画工具04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05Linux下V2Ray安装配置指南06综合整理：pdf预览显示：你尝试预览的文件可能对你的计算机有害。如果你信任此文件以及其来源，请打开此文件以看其内容，如何解决以正常预览文件07jdk21下载、安装（Windows、Linux、macOS）08使用国内镜像网站在线下载安装Qt（解决官网慢的问题）——Qt09Labelme从安装到标注：零基础完整指南10MiniMax-M2 全方位配置手册：覆盖 Claude Code, Cursor, Cline 等工具