数据结构与算法——树和哈希表

VekiSon2025-12-06 21:06

一、树

1.树的基本定义

树是 n（n≥0）个结点的有限集合：

  • 当 n=0 时，称为空树；
  • 非空树中，有且仅有一个根结点；
  • 其余结点可分为 m 个互不相交的子集合（子树），每个子树本身也是一棵独立的树。

2.树的特征

  • 可以动态储存O(1)
  • 查找的速度也比较快O(logn)

3.树的核心概念

用 "家族树" 类比更易理解：

  • 结点的度：结点拥有的子树个数（比如家族中父亲有几个孩子）；
  • 叶结点：度为 0 的结点（无子女的 "晚辈"）；
  • 分支结点：度不为 0 的结点（有子女的 "长辈"）；
  • 树的度数：整棵树中最大的结点度数（家族中生育最多的长辈的子女数）；
  • 树的深度 / 高度：从根开始分层，根为第一层，根的孩子为第二层，依此类推（家族的 "辈分层数"）。

4.二叉树

二叉树是树中最常用的类型，定义为：n 个结点的有限集合，要么为空树，要么由一个根结点 + 两棵互不相交的左子树 和右子树组成。

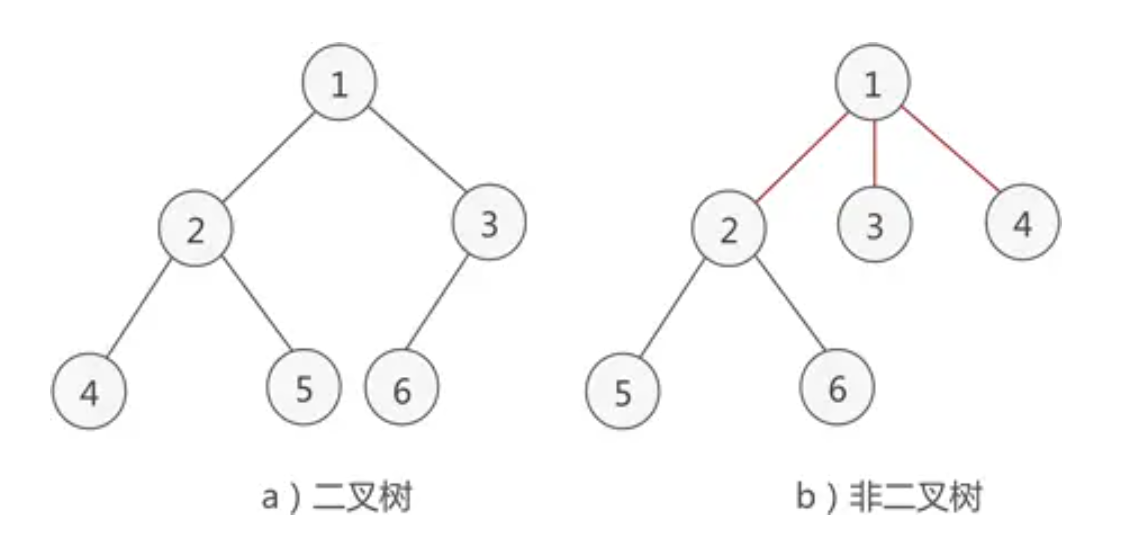
1）二叉树的核心特点

  • 每个结点最多有 2 棵子树（左、右）；
  • 左、右子树有严格顺序，不能颠倒（比如 "左子树是长子，右子树是次子"）；
  • 即使只有一棵子树，也必须区分左 / 右（比如独子也要明确是 "长子"）。

2）特殊二叉树

类型 定义特征
斜树 所有结点只有左子树（左斜树）或只有右子树（右斜树）（类似 "单链" 结构）
满二叉树 所有分支结点都有左右子树，且叶子结点都在同一层（"每层都满" 的二叉树）
完全二叉树 按层序编号后，每个结点的位置与同深度的满二叉树完全一致（"缺最后几个结点" 的满二叉树）

3）二叉树的关键特性

  1. 第 i 层最多有 2^(i-1) 个结点（i≥1）；
  2. 深度为 k 的二叉树至多有 2^k -1 个结点（k≥1）；
  3. 任意二叉树中，叶子结点数 n0 = 度数为2的结点数n2 + 1（推导：总边数 = 总结点数 - 1，而边数 = n1 + 2n2，总结点数 = n0 +n1 +n2，联立得 n0=n2+1）；
  4. n 个结点的完全二叉树深度为 ⌊log₂n⌋ + 1（比如 n=5，log₂5≈2.32，深度 = 2+1=3）。

4）二叉树的遍历

遍历是操作二叉树的基础，分为广度遍历（层序） 和深度遍历（前序 / 中序 / 后序）：

  • 层序遍历：从上到下、从左到右逐层访问结点；
  • 前序遍历：根 → 左 → 右；
  • 中序遍历：左 → 根 → 右；
  • 后序遍历：左 → 右 → 根。

代码实现：

cpp 复制代码 
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

// 二叉树结点定义
typedef struct BinaryTreeNode 
{
    int data;               // 结点数据
    struct BinaryTreeNode *left;  // 左子树指针
    struct BinaryTreeNode *right; // 右子树指针
} BTNode;

// 创建二叉树（递归）
BTNode* CreateBTNode(int data) 
{
    BTNode *node = (BTNode*)malloc(sizeof(BTNode));
    if (!node) 
    {
        perror("malloc failed\n");
        return NULL;
    }
    node->data = data;
    node->left = NULL;
    node->right = NULL;
    return node;
}

// 前序遍历
void PreOrder(BTNode *root) 
{
    if (root == NULL) return;
    printf("%d ", root->data); // 访问根
    PreOrder(root->left);      // 遍历左子树
    PreOrder(root->right);     // 遍历右子树
}

// 中序遍历
void InOrder(BTNode *root) 
{
    if (root == NULL) return;
    InOrder(root->left);       // 遍历左子树
    printf("%d ", root->data); // 访问根
    InOrder(root->right);      // 遍历右子树
}

// 后序遍历
void PostOrder(BTNode *root) 
{
    if (root == NULL) return;
    PostOrder(root->left);     // 遍历左子树
    PostOrder(root->right);    // 遍历右子树
    printf("%d ", root->data); // 访问根
}

// 层序遍历（借助队列）
void LevelOrder(BTNode *root) 
{
    if (root == NULL) return;
    // 简易队列实现
    BTNode *queue[100];
    int front = 0, rear = 0;
    queue[rear++] = root; // 根结点入队

    while (front < rear) 
    {
        BTNode *cur = queue[front++]; // 出队
        printf("%d ", cur->data);     // 访问当前结点
        if (cur->left) queue[rear++] = cur->left; // 左孩子入队
        if (cur->right) queue[rear++] = cur->right; // 右孩子入队
    }
}

// 测试示例
int main() 
{
    // 构建简单二叉树
    BTNode *root = CreateBTNode(1);
    root->left = CreateBTNode(2);
    root->right = CreateBTNode(3);
    root->left->left = CreateBTNode(4);
    root->left->right = CreateBTNode(5);

    printf("前序遍历："); PreOrder(root); printf("\n");
    printf("中序遍历："); InOrder(root); printf("\n");
    printf("后序遍历："); PostOrder(root); printf("\n");
    printf("层序遍历："); LevelOrder(root); printf("\n");

    // 释放内存（简化版，实际需递归释放）
    free(root->left->left);
    free(root->left->right);
    free(root->left);
    free(root->right);
    free(root);
    return 0;
}

输出结果：

复制代码 
前序遍历：1 2 4 5 3 
中序遍历：4 2 5 1 3 
后序遍历：4 5 2 3 1 
层序遍历：1 2 3 4 5

二、哈希表

哈希表（Hash Table）是一种通过 "键 - 值映射" 实现高效存取的结构，核心思想是：存储位置 = f(key)，其中 f 是哈希函数，key 是数据的关键字。

1.哈希表的核心设计

哈希表通常用顺序表（数组） 实现（支持随机访问），目标是让数据的存取效率接近 O (1)，适用于 "海量数据中快速查找" 的场景（比如缓存、字典）。

1）哈希函数设计要点

哈希函数是哈希表的灵魂，需满足两个核心要求：

  • **计算简单：**避免哈希函数本身消耗过多性能；
  • **地址分布均匀：**减少 "哈希冲突" 的概率。

2）常见哈希函数

方法 原理
直接定值法 f (key) = a*key + b（适用于 key 范围已知且连续的场景）
平方取中法 将 key 平方后取中间几位作为地址（适用于 key 分布不规则的场景）
折叠法 将 key 拆分成若干段，求和后取地址（适用于 key 位数较多的场景）
求余法 f (key) = key % size（最常用，size 建议取质数）

2.哈希冲突

当 f(key1) = f(key2) 且 key1≠key2 时，就会发生哈希冲突（不同数据映射到同一数组位置）。常见解决方法：

方法 原理 优缺点
线性探测 冲突后依次尝试 +1、+2、+3... 直到找到空位置 简单但易产生 "聚集"
二次探测 冲突后尝试 +1、-1、+4、-4...（±i²） 缓解聚集，冲突范围更小
随机探测 冲突后尝试 +rand()%size 随机位置 分布更均匀，但需随机数种子

3.哈希表的ADT实现

cpp 复制代码 
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// 定义数据类型
typedef int DATATYPE;
// 哈希表结构体
typedef struct 
{
    DATATYPE* head;  // 数组首地址
    int tlen;        // 数组总长度
} HS_TABLE;

// 哈希函数（求余法）
int HashFunc(DATATYPE key, int size) 
{
    return key % size;
}

// 1. 创建哈希表
HS_TABLE* CreateHsTable(int len) 
{
    if (len <= 0) return NULL;
    HS_TABLE *hs = (HS_TABLE*)malloc(sizeof(HS_TABLE));
    if (!hs) 
    {
        perror("malloc hs failed");
        return NULL;
    }
    // 初始化数组，-1表示空位置
    hs->head = (DATATYPE*)calloc(len, sizeof(DATATYPE));
    if (!hs->head) 
    {
        perror("malloc head failed");
        free(hs);
        return NULL;
    }
    for (int i = 0; i < len; i++) 
    {
        hs->head[i] = -1;
    }
    hs->tlen = len;
    return hs;
}

// 2. 插入数据（线性探测解决冲突）
int InsertHsTable(HS_TABLE* hs, DATATYPE* data) 
{
    if (!hs || !data || hs->head == NULL) return -1;

    int key = *data;
    int idx = HashFunc(key, hs->tlen); // 计算初始位置

    // 线性探测找空位置
    int count = 0;
    while (hs->head[idx] != -1 && count < hs->tlen) 
    {
        idx = (idx + 1) % hs->tlen; // 冲突后+1
        count++;
    }

    // 哈希表满了
    if (count >= hs->tlen) 
    {
        printf("哈希表已满，插入失败\n");
        return -1;
    }

    hs->head[idx] = key;
    return idx; // 返回插入位置
}

// 3. 查找数据
int SearchHsTable(HS_TABLE* hs, DATATYPE* data) 
{
    if (!hs || !data || hs->head == NULL) return -1;

    int key = *data;
    int idx = HashFunc(key, hs->tlen); // 初始位置

    // 线性探测查找
    int count = 0;
    while (hs->head[idx] != key && count < hs->tlen) 
    {
        if (hs->head[idx] == -1) break; // 空位置，说明不存在
        idx = (idx + 1) % hs->tlen;
        count++;
    }

    if (hs->head[idx] == key) 
    {
        return idx; // 找到，返回位置
    }
    else
    {
        return -1;  // 未找到
    }
}

// 4. 销毁哈希表
int DestroyHsTable(HS_TABLE* hs) 
{
    if (!hs) return -1;
    if (hs->head) 
    {
        free(hs->head);
        hs->head = NULL;
    }
    free(hs);
    return 0;
}

// 测试示例
int main() 
{
    // 创建长度为10的哈希表
    HS_TABLE *hs = CreateHsTable(10);
    if (!hs) return -1;

    // 插入数据
    int data1 = 12, data2 = 22, data3 = 33;
    printf("插入%d的位置：%d\n", data1, InsertHsTable(hs, &data1));
    printf("插入%d的位置：%d\n", data2, InsertHsTable(hs, &data2));
    printf("插入%d的位置：%d\n", data3, InsertHsTable(hs, &data3));

    // 查找数据
    int find_data = 22;
    int find_idx = SearchHsTable(hs, &find_data);
    if (find_idx != -1) 
    {
        printf("找到%d，位置：%d\n", find_data, find_idx);
    } 
    else 
    {
        printf("未找到%d\n", find_data);
    }

    // 销毁哈希表
    DestroyHsTable(hs);
    return 0;
}

输出结果：

复制代码 
插入12的位置：2
插入22的位置：3
插入33的位置：3
找到22，位置：3

三、总结

树和哈希表是 C 语言数据结构中最常用的两种结构：

  • 二叉树的核心是 "层级有序"，遍历是操作的基础，需掌握前 / 中 / 后 / 层序四种遍历方式；
  • 哈希表的核心是 "哈希函数 + 冲突解决"，求余法是最常用的哈希函数，线性探测是最易实现的冲突解决方式。
相关推荐
xu_yule2 小时前
数据结构与算法（1）（第一章复杂度知识点）（大O渐进表示法）
数据结构
大江东去浪淘尽千古风流人物2 小时前
【DSP】向量化操作的误差来源分析及其经典解决方案
linux·运维·人工智能·算法·vr·dsp开发·mr
fish_xk2 小时前
数据结构之排序
数据结构
Unstoppable223 小时前
代码随想录算法训练营第 56 天 | 拓扑排序精讲、Dijkstra（朴素版）精讲
java·数据结构·算法·图
potato_may3 小时前
CC++ 内存管理 —— 程序的“五脏六腑”在哪里？
c语言·开发语言·数据结构·c++·内存·内存管理
饕餮怪程序猿3 小时前
A*算法（C++实现）
开发语言·c++·算法
电饭叔3 小时前
不含Luhn算法《python语言程序设计》2018版--第8章14题利用字符串输入作为一个信用卡号之二（识别卡号有效）
java·python·算法
2301_800256114 小时前
8.2 空间查询基本组件 核心知识点总结
数据库·人工智能·算法
不穿格子的程序员4 小时前
从零开始写算法——矩阵类题：矩阵置零 + 螺旋矩阵
线性代数·算法·矩阵
热门推荐
01GitHub 镜像站点02React CVE-2025-55182漏洞排查与修复指南03【超详细教程】手把手教你从微软官网免费下载Windows 10官方原版ISO镜像（2025最新版）04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05UV安装并设置国内源06BongoCat - 跨平台键盘猫动画工具07打造高效订单处理！ZKmall开源商城的统一履约中心架构解析08智能库存管理的需求预测模型：从业务痛点到落地代码的完整实践09本地部署阿里最新开源的Z-Image10Linux下V2Ray安装配置指南