数维杯秋季赛正式开赛,数维杯为美赛开赛前第一场英文数模竞赛,比赛时间为五至下周二,美赛前(2026年1月中旬)出成绩,难度约为美赛0.6,题目类型与美赛相似,适合练手。本文将为大家带来D题详细版思路,为大家介绍D赛题需要解决的问题、涉及的模型、解题所需要的知识以及后续可能存在的难点。
D题的求解思路可以分为两大方向一收集数据,基于真实的洋流、温度数据构建三维模型;二基于公开文献/简化物理规律,设置简单网格或者单点预测模型建模。
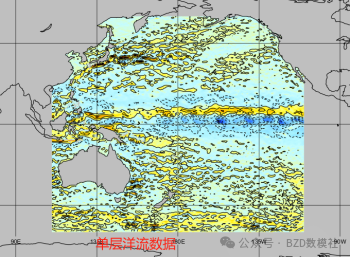
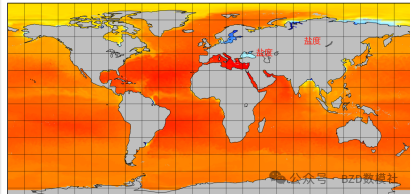
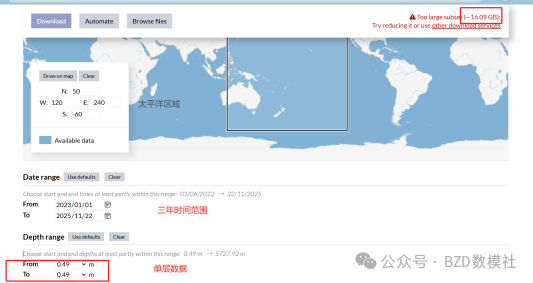
两种思路主要区别在于是否需要数据,以洋流数据为例,我们需要收集2023-2025年日平均单层数据就需要16g,一共50层。单独洋流数据全部下载需要800G,温度、盐度也为1T左右,针对96小时的数模竞赛,对网速、计算机存储、计算机配置都是非常高的挑战。因此,本论文针对第一种思路最后会尝试只针对日本附近构建小的三维模型(5G左右数据量)做展示。
第二种思路数据量较小可控制在1G左右,对大家的存储、配置会更加合适。下面分别介绍两种思路的大致方案。蓝色为第一方案,绿色为第二方案
任务1:核废水全球海洋扩散建模
****目标:****模拟核废水在0--10年内三维扩散路径,计算上海、洛杉矶、釜山邻近海域最早到达时间与浓度曲线。
****输入:****2023--2025年三大洋流速/方向、温盐、潮汐、Argo浮标、海底地形数据。
****输出:****时空浓度场,目标海域
第一种方案
必要假设 :核废水瞬时点源排放,初始体积可忽略;流场数据为年均值+ 季节扰动(可加随机项);放射性核素以保守示踪剂为主(不考虑生物降解,仅衰变);扩散遵循对流-扩散-衰变方程;

第二种方案
|--------|----------------------------|----------------|
| 参数 | 值 | 来源 |
| 排放点 | (37.42°N, 141.03°E, 深度30m) | TEPCO |
| 年排放量 | 4.5万吨 ≈ | 官方 |
| 氚初始浓度 | 1.5×10⁶ Bq/L | IAEA |
| 黑潮流速 | 0.5--1.5 m/s | Wikipedia/NOAA |
| 水平扩散系数 | | Okubo图 |

任务2:典型国家影响程度建模与风险分级
构建海洋生态 + 渔业经济 + 食品安全三维评价体系 → 输出高/中/低风险国家及核心指标曲线。
海洋生态(关键生态系统放射性核素累积量、浮游生物死亡率)、
渔业经济(30年渔获量减少率、出口量损失)、
食品安全(居民通过海鲜摄入的放射性核素剂量)

第二种做法
|----|-----------|--------------|-----------|----------|
| 国家 | 距离排放点(km) | 最早到达(年)问题一结果 | 富集因子(BCF) | 渔业依赖度(%) |
| 韩国 | 900 | 0.8 | 1(近海) | 85 |
| 中国 | 1800 | 1.7 | 0.6 | 60 |
| 美国 | 7500 | 3.4 | 0.2 | 30 |
任务3:核废水处理方案建模与优化决策
针对三种处理方案(当前海洋排放、强化处理+长期储存、零海洋排放),收集福岛核电站相关数据,建立涵盖成本、环境影响、安全时间的三维评价模型。量化各方案30年的海洋环境影响、总成本及放射性核素衰变达标时间,并进行多目标优化。
|---------|-------------|-------------|
| 方案 | 描述 | 关键参数 |
| A. 排海 | 当前ALPS处理后排放 | 每年4.5万吨,30年 |
| B. 强化+储 | 二次处理+混凝土固化 | 成本×3,排放为0 |
| C. 零排海 | 电解/蒸馏/长期陆储 | 成本×10,环境影响0 |