深入浅出蓝桥杯：算法基础概念与实战应用（三）搜索

铭哥的编程日记2025-11-18 20:20

算法基础概念与实战应用（三）搜索

文章目录

  • 算法基础概念与实战应用（三）搜索
  • [1.1 深度优先搜索 - DFS](#1.1 深度优先搜索 - DFS)
    • [1.1.1 枚举⼦集](#1.1.1 枚举⼦集)
    • [1.1.2 组合型枚举](#1.1.2 组合型枚举)
    • [1.1.3 枚举排列](#1.1.3 枚举排列)
    • [1.1.4 全排列问题](#1.1.4 全排列问题)
  • [1.2 DFS](#1.2 DFS)
    • [1.2.1 选数](#1.2.1 选数)
    • [1.2.2 ⻜机降落](#1.2.2 ⻜机降落)
    • [1.2.3 ⼋皇后](#1.2.3 ⼋皇后)
    • [1.2.4 数独](#1.2.4 数独)
  • [1.3 剪枝与优化](#1.3 剪枝与优化)
    • [1.3.1 数的划分](#1.3.1 数的划分)
    • [1.3.2 ⼩猫爬⼭](#1.3.2 ⼩猫爬⼭)
  • [1.4 记忆化搜索](#1.4 记忆化搜索)
    • [1.4.1 Function](#1.4.1 Function)
    • [1.4.2 天下第⼀](#1.4.2 天下第⼀)
    • [1.4.3 滑雪](#1.4.3 滑雪)
  • [2. 宽度优先搜索 - BFS](#2. 宽度优先搜索 - BFS)
  • 整体源代码总结

1.1 深度优先搜索 - DFS

1.1.1 枚举⼦集

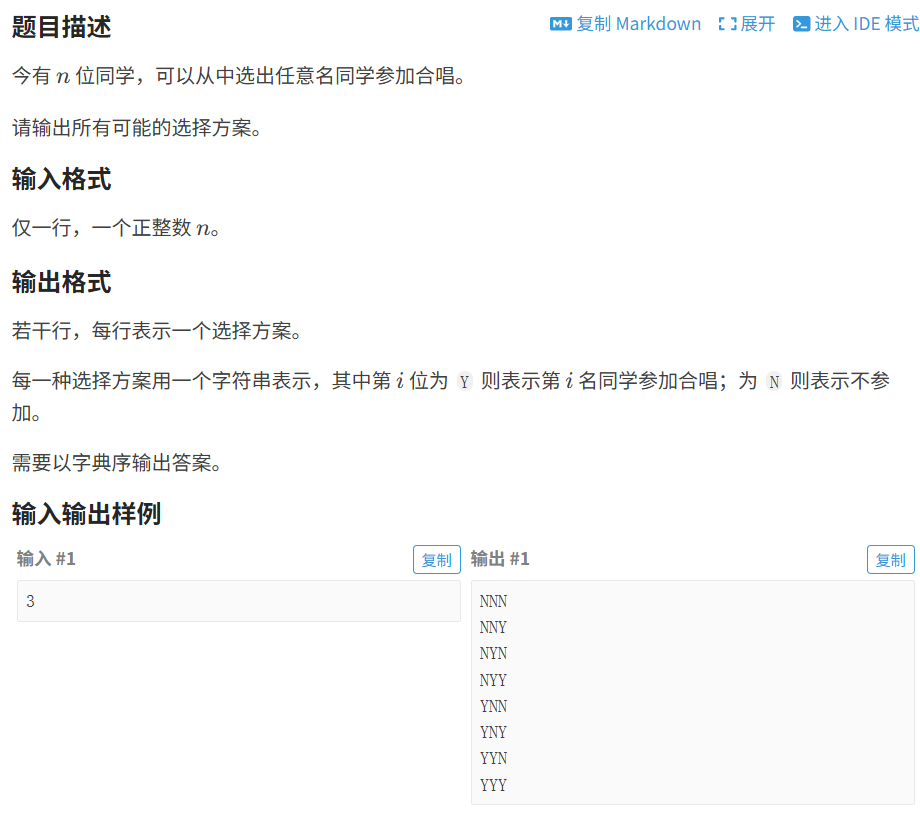
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
int n;
string path; // 记录递归过程中，每⼀步的决策
void dfs(int pos)
{
	if (pos > n)
	{
		// path 就存着前 n 个⼈的决策
		cout << path << endl;
		return;
	}
	// 不选
	path += 'N';
	dfs(pos + 1);
	path.pop_back(); // 回溯，清空现场
	// 选
	path += 'Y';
	dfs(pos + 1);
	path.pop_back(); // 清空现场
}
int main()
{
	cin >> n;
	dfs(1);
	return 0;
}

1.1.2 组合型枚举

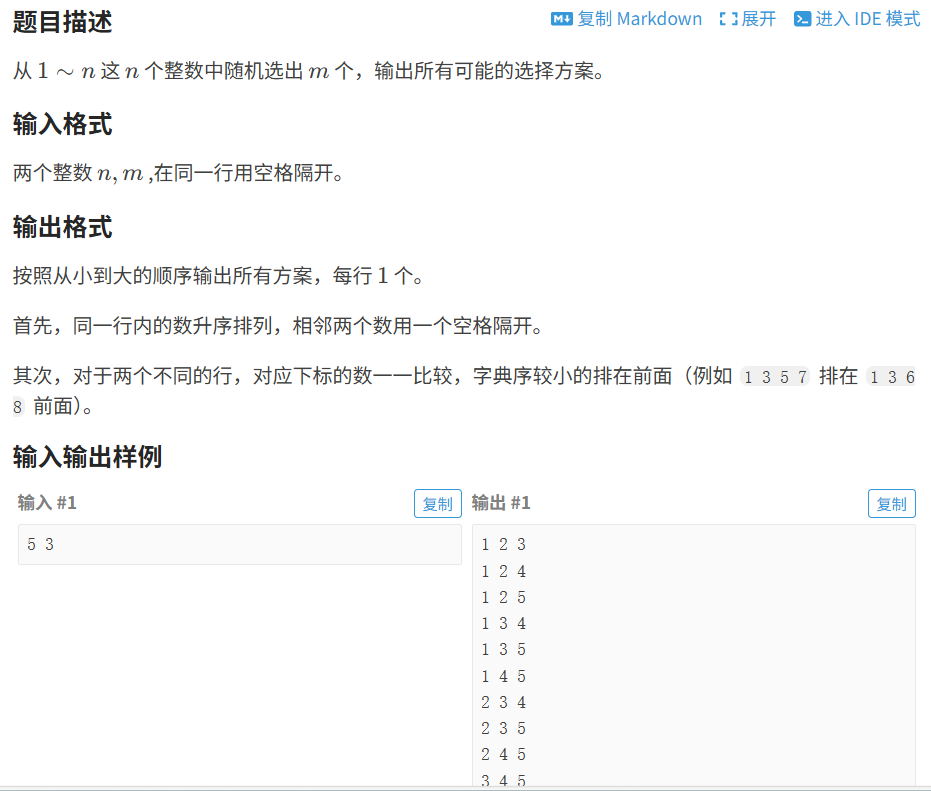
代码如下（示例）：

c 复制代码 
#include <iostream>
#include <vector>
using namespace std;
int n, m;
vector<int> path;
// path.size();
void dfs(int begin)
{
	if (path.size() == m)
	{
		for (auto x : path) cout << x << " ";
		cout << endl;
		return;
	}
	for (int i = begin; i <= n; i++)
	{
		path.push_back(i);
		dfs(i + 1);
		path.pop_back(); // 清空现场
	}
}
int main()
{
	cin >> n >> m;
	dfs(1);
	return 0;
}

1.1.3 枚举排列

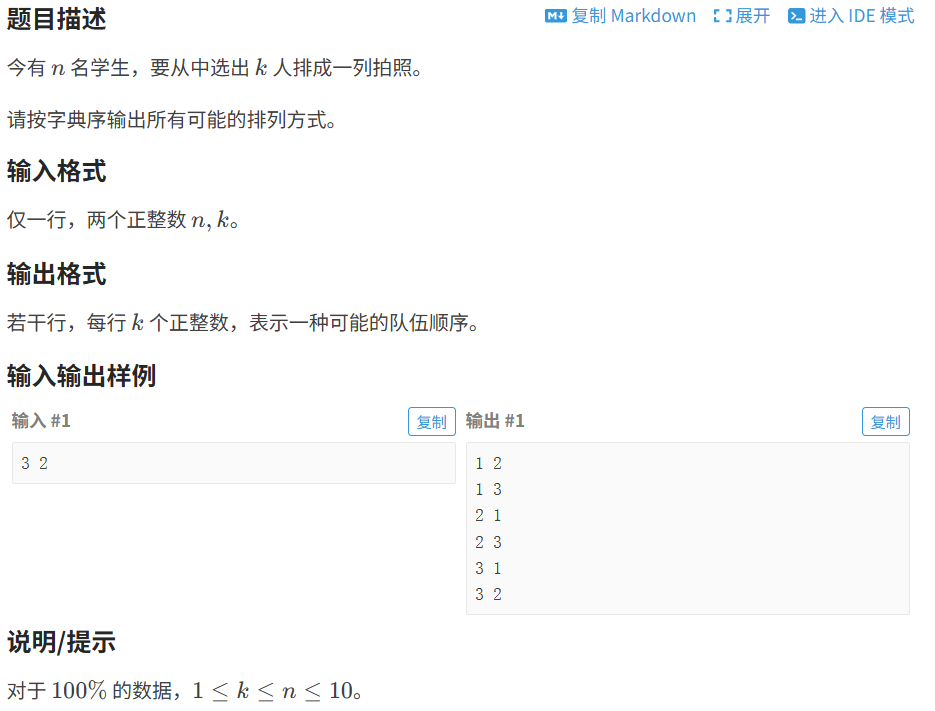
代码如下（示例）：

c 复制代码 
#include <iostream>
#include <vector>
using namespace std;
const int N = 15;
int n, k;
vector<int> path;
bool st[N]; // 标记⼀下哪些数已经选过了
void dfs()
{
	if (path.size() == k)
	{
		for (auto x : path) cout << x << " ";
		cout << endl;
		return;
	}
	for (int i = 1; i <= n; i++)
	{
		if (st[i]) continue;
		path.push_back(i);
		st[i] = true;
		dfs();
		// 恢复现场
		path.pop_back();
		st[i] = false;
	}
}
int main()
{
	cin >> n >> k;
	dfs();
	return 0;
}

1.1.4 全排列问题

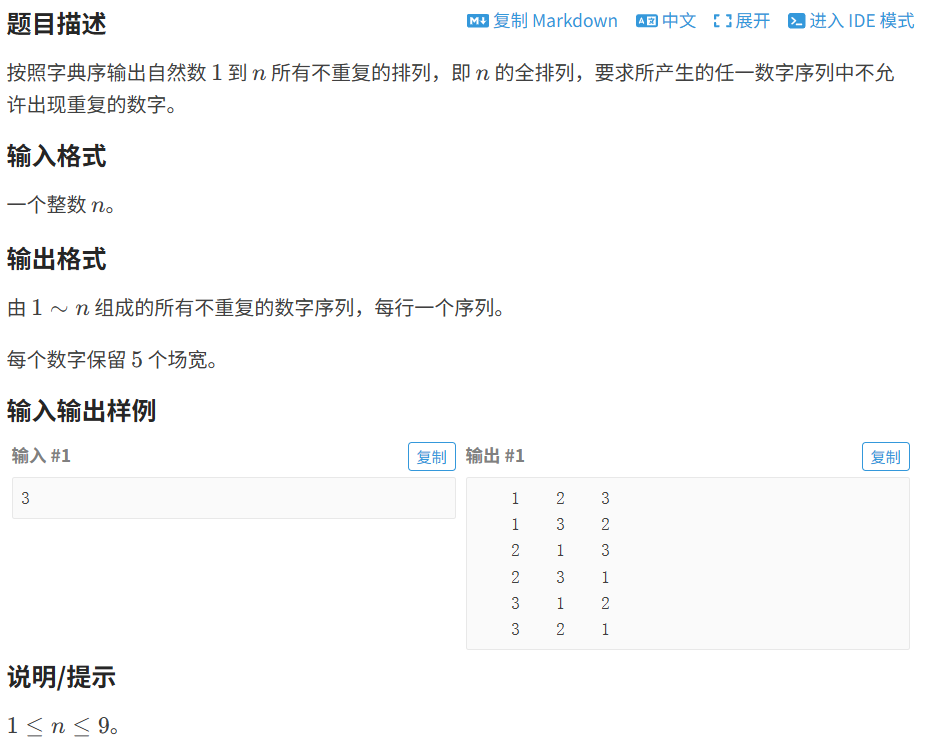
代码如下（示例）：

c 复制代码 
#include <iostream>
#include <vector>
using namespace std;
const int N = 15;
int n;
bool st[N];
vector<int> path;
void dfs()
{
	if (path.size() == n)
	{
		for (auto x : path)
		{
			printf("%5d", x);
		}
		cout << endl;
		return;
	}
	for (int i = 1; i <= n; i++)
	{
		if (st[i]) continue;
		path.push_back(i);
		st[i] = true;
		dfs();
		// 恢复现场
		path.pop_back();
		st[i] = false;
	}
}
int main()
{
	cin >> n;
	dfs();
	return 0;
}

1.2 DFS

1.2.1 选数

代码如下（示例）：

c 复制代码 
#include<iostream>
using namespace std;
const int N = 25;
int n, k;
int a[N];
int ret;
int path; // 记录路径中所选择的数的和
bool isprime(int x)
{
	if (x <= 1) return false;
	// 试除法
	for (int i = 2; i <= x / i; i++)
	{
		if (x % i == 0) return false;
	}
	return true;
}
void dfs(int pos, int begin)
{
	if (pos > k)
	{
		if (isprime(path)) ret++;
		return;
	}
	for (int i = begin; i <= n; i++)
	{
		path += a[i];
		dfs(pos + 1, i + 1);
		path -= a[i]; // 恢复现场
	}
}
int main()
{
	cin >> n >> k;
	for (int i = 1; i <= n; i++) cin >> a[i];
	dfs(1, 1);
	cout << ret << endl;
	return 0;
}

1.2.2 ⻜机降落


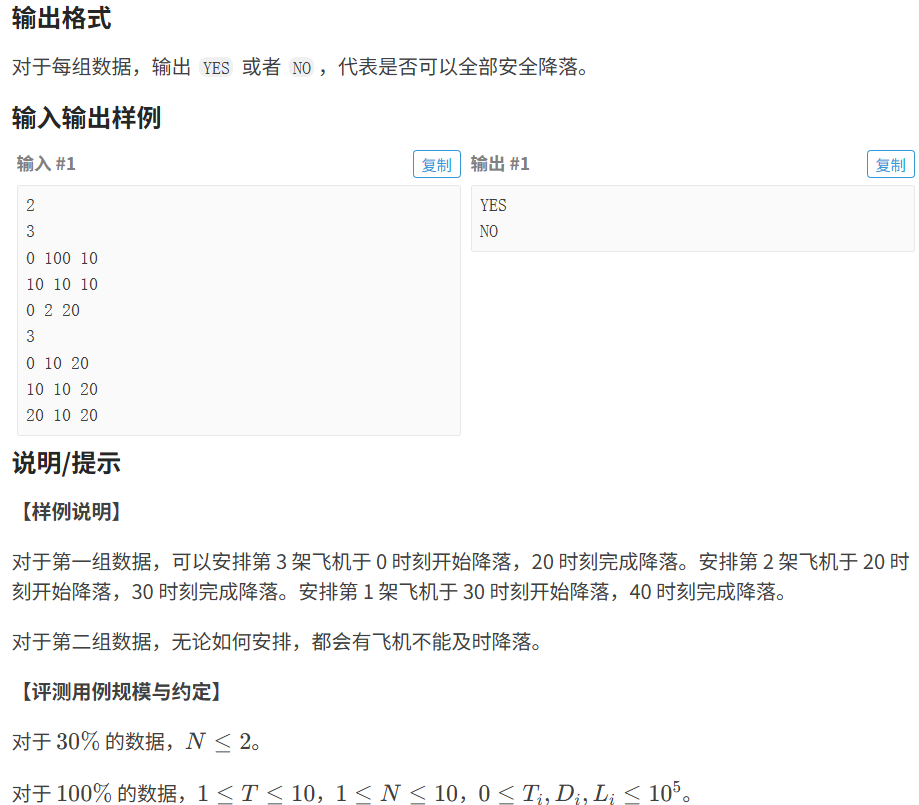
代码如下（示例）：

c 复制代码 
#include <iostream>
#include <cstring>
using namespace std;
const int N = 15;
int n;
int t[N], d[N], l[N];
bool st[N]; // 标记路径中哪些⻜机已经摆放过
bool dfs(int pos, int end)
{
	if (pos > n)
	{
		return true;
	}
	for (int i = 1; i <= n; i++)
	{
		if (st[i] == true) continue; // 剪枝
		if (end > t[i] + d[i]) continue; // 剪枝
		int newend = max(t[i], end) + l[i];
		st[i] = true;
		if (dfs(pos + 1, newend)) return true;
		st[i] = false; // 回复现场
	}
	return false;
}
int main()
{
	int T; cin >> T;
	while (T--) // 多组测试数据的时候，⼀定要注意清空数据
	{
		memset(st, 0, sizeof st);
		cin >> n;
		for (int i = 1; i <= n; i++) cin >> t[i] >> d[i] >> l[i];
		if (dfs(1, 0)) cout << "YES" << endl;
		else cout << "NO" << endl;
	}
	return 0;
}

1.2.3 ⼋皇后



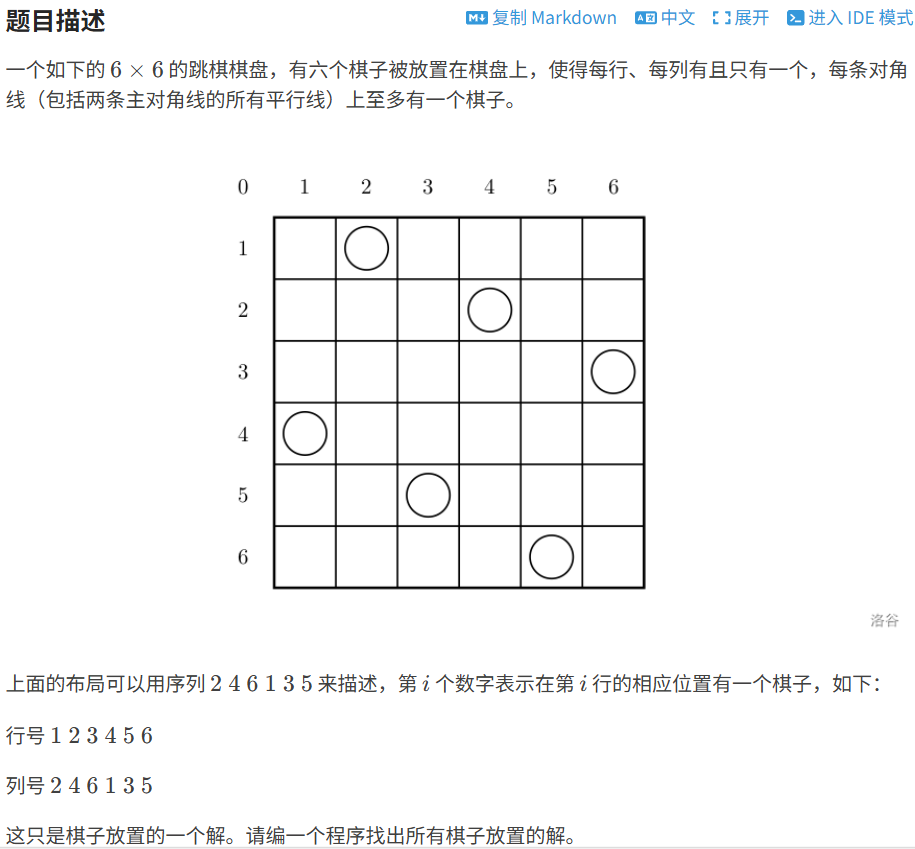
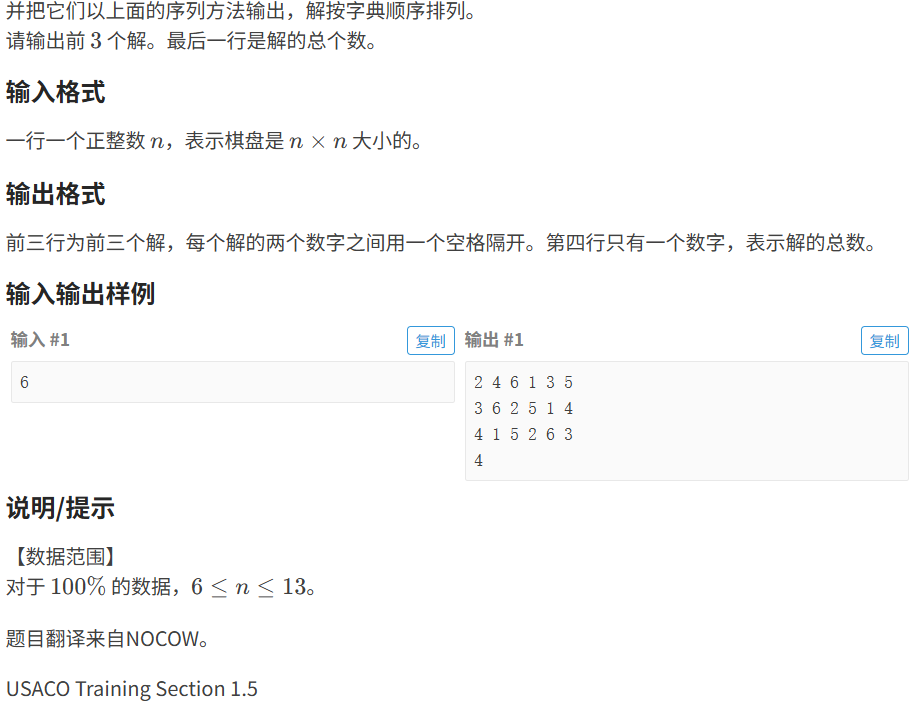
代码如下（示例）：

c 复制代码 
#include <iostream>
#include <vector>
using namespace std;
const int N = 15;
int n;
bool col[N], st1[N * 2], st2[N * 2];
int ret;
vector<int> path;
void dfs(int x)
{
	if (x > n)
	{
		ret++;
		if (ret <= 3)
		{
			for (auto x : path) cout << x << " ";
			cout << endl;
		}
		return;
	}
	for (int y = 1; y <= n; y++)
	{
		// 判断能不能摆在这⼀列
		if (col[y] || st1[y - x + n] || st2[y + x]) continue; // 剪枝
		col[y] = st1[y - x + n] = st2[y + x] = true;
		path.push_back(y);
		dfs(x + 1);
		col[y] = st1[y - x + n] = st2[y + x] = false;
		path.pop_back();
	}
}
int main()
{
	cin >> n;
	dfs(1);
	cout << ret << endl;
	return 0;
}

1.2.4 数独



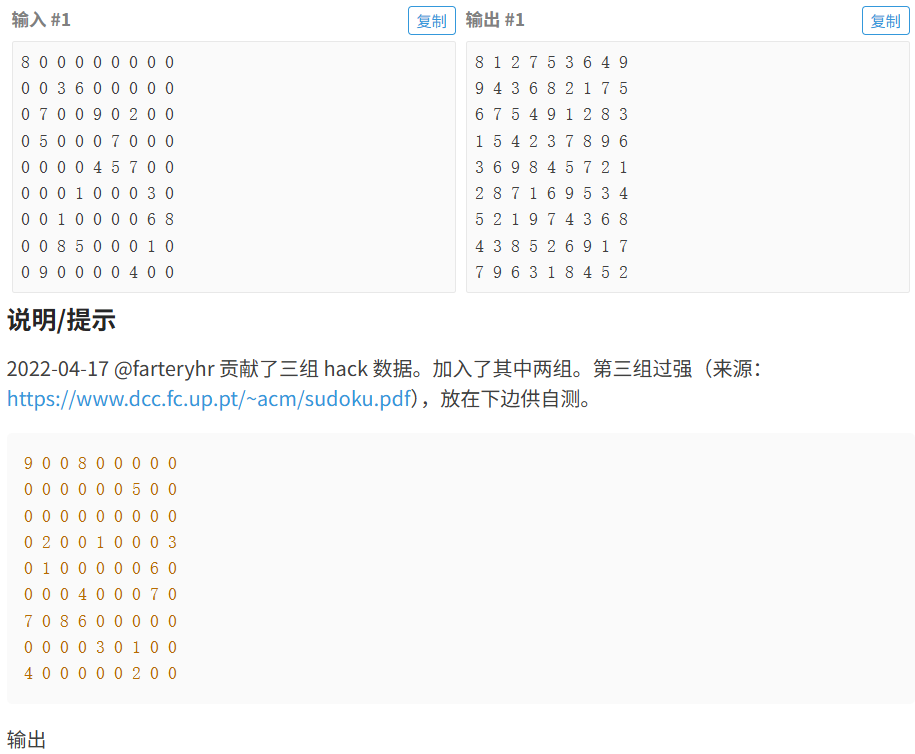
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
const int N = 10;
int n = 9;
int a[N][N];
bool row[N][N], col[N][N], st[N][N][N];
bool dfs(int i, int j)
{
	if (j == n)
	{
		// 当这⼀⾏填满之后
		i++;
		j = 0;
	}
	if (i == n) return true; // 找到⼀种合法的情况，就停⽌递归
	if (a[i][j]) return dfs(i, j + 1);
	for (int x = 1; x <= 9; x++)
	{
		if (row[i][x] || col[j][x] || st[i / 3][j / 3][x]) continue; // 剪枝
		row[i][x] = col[j][x] = st[i / 3][j / 3][x] = true;
		a[i][j] = x;
		if (dfs(i, j + 1)) return true;
		// 恢复现场
		row[i][x] = col[j][x] = st[i / 3][j / 3][x] = false;
		a[i][j] = 0;
	}
	return false;
}
int main()
{
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			cin >> a[i][j];
			int x = a[i][j];
			if (x)
			{
				// 标记⼀下
				row[i][x] = col[j][x] = st[i / 3][j / 3][x] = true;
			}
		}
	}
	dfs(0, 0);
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			cout << a[i][j] << " ";
		}
	}
	return 0;
}

1.3 剪枝与优化

1.3.1 数的划分

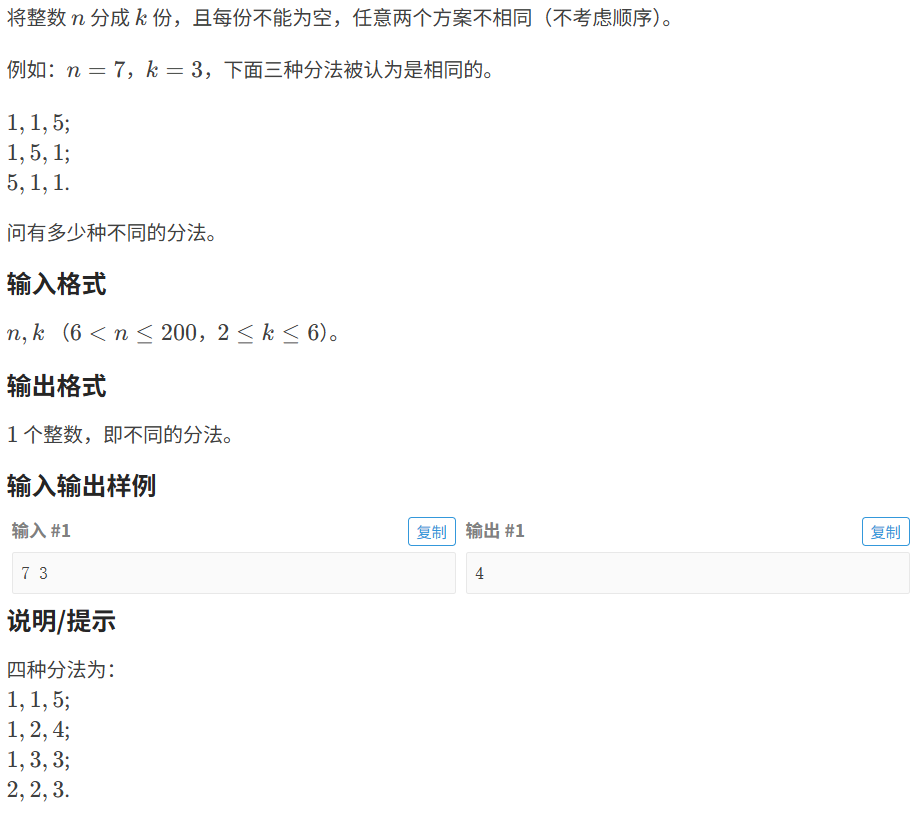
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
int n, k;
int path, ret;
void dfs(int pos, int begin)
{
	if (pos == k)
	{
		if (path == n) ret++;
		return;
	}
	// 可⾏性剪枝
	// if(path + begin * (k - pos) > n) return;
	for (int i = begin; i <= n; i++)
	{
		// 可⾏性剪枝
		if (path + i * (k - pos) > n) return;
		path += i;
		dfs(pos + 1, i);
		path -= i;
	}
}
int main()
{
	cin >> n >> k;
	dfs(0, 1);           
	cout << ret << endl;
	return 0;
}

1.3.2 ⼩猫爬⼭

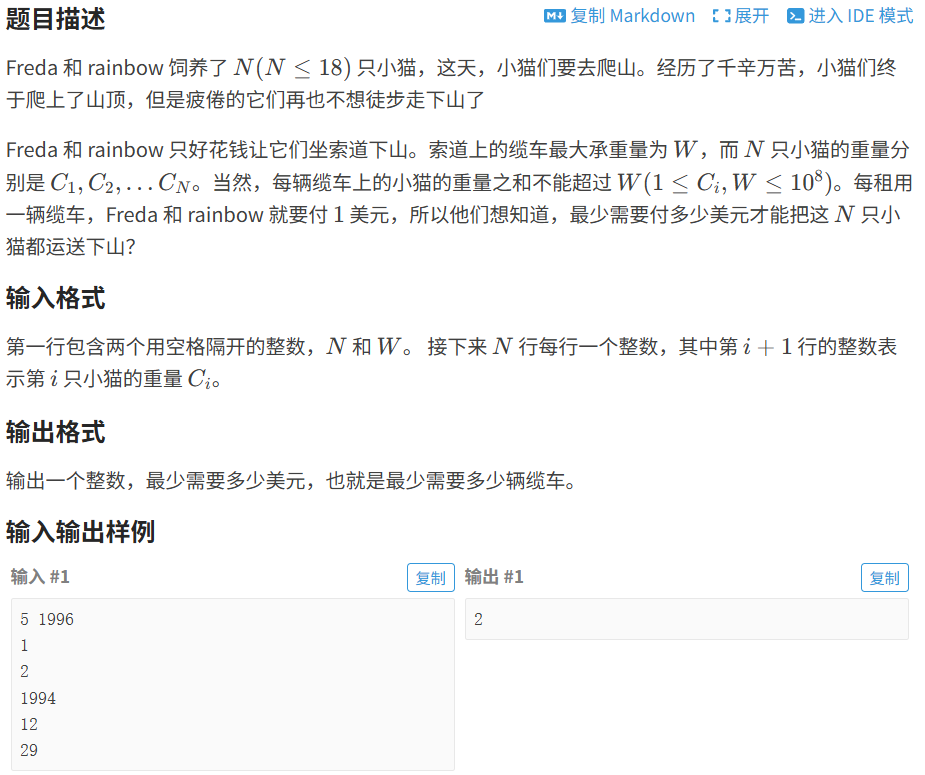
代码如下（示例）：

c 复制代码 
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 20;
int n, w;
int c[N]; // ⼩猫的信息
int cnt; // 当前⽤了多少⻋
int s[N]; // 每⼀辆⻋⽬前的总重
int ret = N; // 最优解
bool cmp(int a, int b)
{
	return a > b;
}
void dfs(int pos)
{
	// 策略⼆：最优性剪枝
	if (cnt >= ret) return;
	if (pos > n)
	{
		ret = cnt;
		return;
	}
	// 策略三：优化搜索顺序
	// 先安排在已有的⻋辆上
	for (int i = 1; i <= cnt; i++)
	{
		// 策略⼀：可⾏性剪枝
		if (s[i] + c[pos] > w) continue;
		s[i] += c[pos];
		dfs(pos + 1);
		s[i] -= c[pos]; // 恢复现场
	}
	// 重开⼀辆⻋
	cnt++;
	s[cnt] = c[pos];
	dfs(pos + 1);
	// 恢复现场
	s[cnt] = 0;
	cnt--;
}
int main()
{
	cin >> n >> w;
	for (int i = 1; i <= n; i++) cin >> c[i];
	// 策略三：优化搜索顺序
	sort(c + 1, c + 1 + n, cmp);
	dfs(1);
	cout << ret << endl;
	return 0;
}

1.4 记忆化搜索

1.4.1 Function


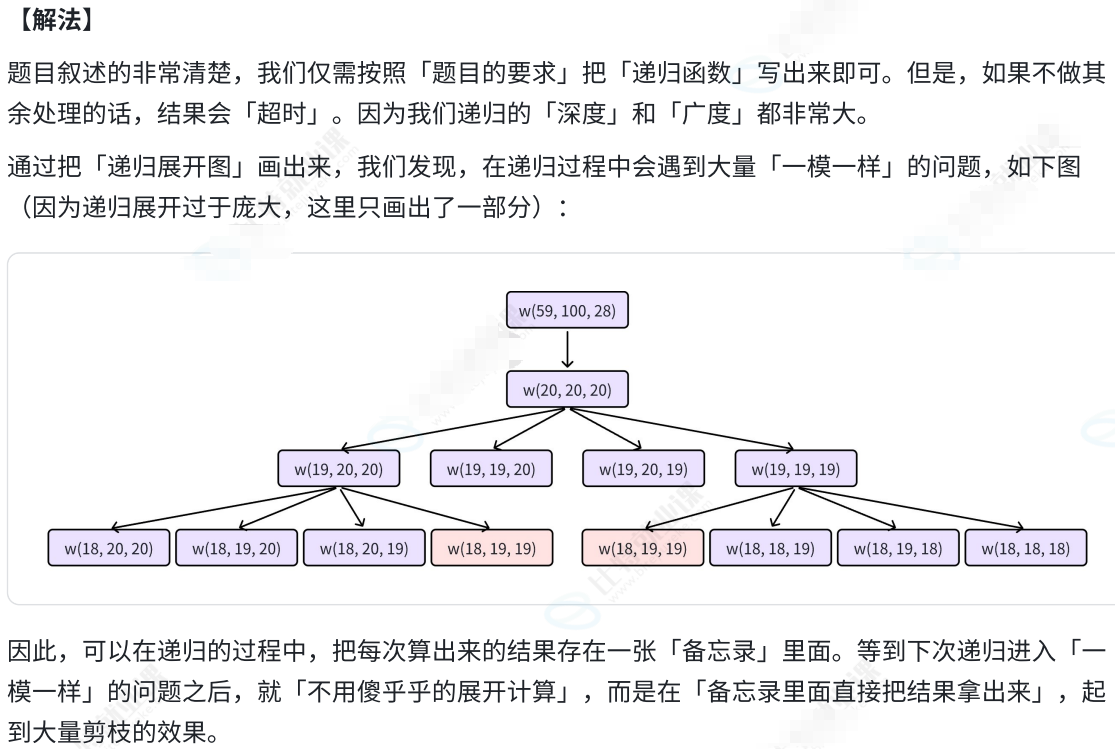
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 25;
LL a, b, c;
LL f[N][N][N]; // 备忘录
LL dfs(LL a, LL b, LL c)
{
	if (a <= 0 || b <= 0 || c <= 0) return 1;
	if (a > 20 || b > 20 || c > 20) return dfs(20, 20, 20);
	if (f[a][b][c]) return f[a][b][c];
	if (a < b && b < c) return f[a][b][c] = dfs(a, b, c - 1) + dfs(a, b - 1, c
		- 1) - dfs(a, b - 1, c);
	else return f[a][b][c] = dfs(a - 1, b, c) + dfs(a - 1, b - 1, c) + dfs(a
		- 1, b, c - 1) - dfs(a - 1, b - 1, c - 1);
}
int main()
{
	while (cin >> a >> b >> c)
	{
		// 多组测试数据：不需要清空
		if (a == -1 && b == -1 && c == -1) break;
		printf("w(%lld, %lld, %lld) = %lld\n", a, b, c, dfs(a, b, c));
	}
	return 0;
}

1.4.2 天下第⼀


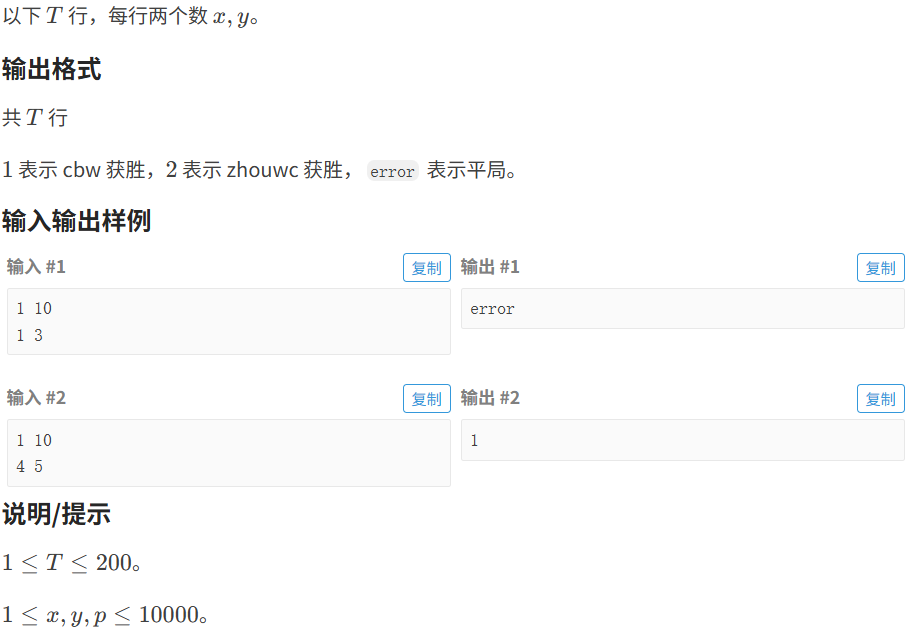
代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
const int N = 1e4 + 10;
int x, y, p;
char f[N][N]; // 备忘录
char dfs(int x, int y)
{
	if (f[x][y]) return f[x][y]; // 剪枝
	f[x][y] = '3'; // 这个状态已经访问过了，之后再遇到时，表⽰平局
	if (x == 0) return f[x][y] = '1';
	if (y == 0) return f[x][y] = '2';
	return f[x][y] = dfs((x + y) % p, (x + y + y) % p);
}
int main()
{
	int T; cin >> T >> p;
	while (T--)
	{
		cin >> x >> y;
		char ret = dfs(x, y);
		if (ret == '1') cout << 1 << endl;
		else if (ret == '2') cout << 2 << endl;
		else cout << "error" << endl;
	}
}

1.4.3 滑雪


代码如下（示例）：

c 复制代码 
#include <iostream>
using namespace std;
const int N = 110;
int n, m;
int a[N][N];
int f[N][N]; // 备忘录
int dx[] = { 0, 0, 1, -1 };
int dy[] = { 1, -1, 0, 0 };
int dfs(int i, int j)
{
	if (f[i][j]) return f[i][j];
	int len = 1;
	// 上下左右四个⽅向搜
	for (int k = 0; k < 4; k++)
	{
		int x = i + dx[k], y = j + dy[k];
		if (x < 1 || x > n || y < 1 || y > m) continue;
		if (a[i][j] <= a[x][y]) continue;
		len = max(dfs(x, y) + 1, len);
	}
	return f[i][j] = len;
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
			cin >> a[i][j];
	int ret = 1;
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
			ret = max(ret, dfs(i, j));
	cout << ret << endl;
	return 0;
}

2. 宽度优先搜索 - BFS

整体源代码总结

代码如下（示例）：

c 复制代码
相关推荐
2501_941111892 小时前
低延迟系统C++优化
开发语言·c++·算法
2501_941111992 小时前
C++中的装饰器模式变体
开发语言·c++·算法
Espresso Macchiato3 小时前
Leetcode 3748. Count Stable Subarrays
算法·leetcode·职场和发展·leetcode hard·leetcode 3748·leetcode周赛476·区间求和
大袁同学3 小时前
【哈希hash】：程序的“魔法索引”，实现数据瞬移
数据结构·c++·算法·哈希算法·散列表
一水鉴天3 小时前
整体设计 全面梳理复盘 之39 生态工具链 到顶级表征及其完全公理化
大数据·人工智能·算法
Moonbit3 小时前
入围名单公布｜2025 MGPIC 决赛即将拉开帷幕！
后端·算法
2501_941112614 小时前
C++与Docker集成开发
开发语言·c++·算法
智者知已应修善业4 小时前
【51单片机：两边向中间流水：即两边先点亮然后熄灭，次边的点亮再熄灭，直到最中间的两个点亮再熄灭，然后重复动作。】2023-3-4
c语言·c++·经验分享·笔记·嵌入式硬件·算法·51单片机
热门推荐
01GitHub 镜像站点02今天 Cloudflare 全球事故，连 GPT 和你的网站都一起“掉线”了03UV安装并设置国内源04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05BongoCat - 跨平台键盘猫动画工具06Linux下V2Ray安装配置指南07Valdi：Snapchat 开源的新一代跨平台 UI 框架08Labelme从安装到标注：零基础完整指南092025 最新教程：注册并切换到美区 Apple ID10Visual Studio Code设置个性化背景教程