【元启发算法】SMA黏菌算法：当自然智慧走进代码世界

[🧩 困境：当传统算法遇上 "迷宫"](#🧩 困境：当传统算法遇上 "迷宫")

[🌱 原理：黏菌的生存哲学与算法映射](#🌱 原理：黏菌的生存哲学与算法映射)

[1. 扩散与探索：像黏菌一样 "感知世界"](#1. 扩散与探索：像黏菌一样 "感知世界")

[2. 聚集与收缩：向优质解靠拢](#2. 聚集与收缩：向优质解靠拢)

[3. 波动与优化：在平衡中逼近最优](#3. 波动与优化：在平衡中逼近最优)

[📊 数学之美：从生物行为到代码逻辑](#📊 数学之美：从生物行为到代码逻辑)

[💻 代码实现：让黏菌在屏幕上 "生长"](#💻 代码实现：让黏菌在屏幕上 "生长")

运行说明：

[🔍 结果解读：从图像看黏菌的 "思考"](#🔍 结果解读：从图像看黏菌的 "思考")

[🌍 现实应用：从实验室到产业界](#🌍 现实应用：从实验室到产业界)

[🌱 结语：向自然学习的算法哲学](#🌱 结语：向自然学习的算法哲学)

清晨的林间，一团淡黄色的生物在腐木上缓缓蠕动。它没有大脑，没有神经，却能在迷宫般的落叶间探出最优路径，精准覆盖每一处食物源。这便是黏菌 ------ 自然界最朴素的 "路径规划大师"。

"最简单的生命，藏着最深刻的优化智慧。" 当计算机科学家凝视这团原生质时，一个灵感破土而出：能否让机器像黏菌一样，在复杂问题中找到那条隐藏的捷径？黏菌算法（Slime Mold Algorithm, SMA）由此诞生，它用代码复刻了生物的生存智慧，成为解决工程优化问题的利器。

🧩 困境：当传统算法遇上 "迷宫"

想象你是一位物流调度员，需要为 100 辆货车规划最优配送路线。每条路线要避开拥堵、满足时效、降低油耗 ------ 这就像在万亿条可能的路径中找到唯一的 "黄金通道"。

传统优化算法面对这类问题常常陷入困境：

枚举法如同让蚂蚁遍历地球，计算量大到无法承受
贪婪法容易 "一条道走到黑"，困在局部最优解里
遗传算法的交叉变异策略，在高维度问题中效率骤降

而黏菌在自然界早已给出答案：它通过伸缩细胞质的 "脉动"，既能大范围探索未知区域，又能精准收缩到优质路径。这种 "探索 - 开发" 的平衡艺术，正是 SMA 算法的核心灵感。

🌱 原理：黏菌的生存哲学与算法映射

黏菌的觅食行为可拆解为三个关键阶段，每个阶段都对应着算法的核心逻辑：

1. 扩散与探索：像黏菌一样 "感知世界"

当黏菌处于饥饿状态时，会伸出无数伪足探索周围环境。算法中，这一过程被抽象为 "种群初始化"：

随机生成大量候选解（类似黏菌的伪足）
每个解对应问题的一种可能方案（如一条配送路线）
通过适应度函数评估解的优劣（类似黏菌对食物的 "感知"）

生活化类比：这就像盲人摸象，先让足够多的人从不同角度触摸，才能拼凑出大象的轮廓。

2. 聚集与收缩：向优质解靠拢

当某条伪足发现食物，黏菌会收缩其他方向的细胞质，向食物源聚集。算法中，这通过 "权重更新" 实现：

适应度高的解（优质路径）会获得更高权重
其他解逐渐向高权重解靠近（类似细胞质流动）
引入随机因子避免过早收敛（保留探索能力）

核心公式的通俗解读：

复制代码

X(i,j) = Xb(j) + vb×(|X(i,j) - Xb(j)|) × log(1/r)  （当r < p）

Xb (j)：当前最优解（食物源位置）
vb：权重系数（类似细胞质流动强度）
r 和 p：随机数（模拟自然环境的不确定性）

类比解释：这就像一群登山者，当有人发现更高的山峰时，大家会向他靠拢，但每个人的步伐又带有随机性，避免错过隐藏的更高峰。

3. 波动与优化：在平衡中逼近最优

黏菌的细胞质会持续脉动，这种波动能让它在已发现的食物周围做精细探索。算法中，这通过 "动态调整参数" 实现：

随着迭代进行，探索范围逐渐缩小（强化局部开发）
引入 "负反馈机制"，防止过度聚集（保持多样性）
最终收敛到全局最优解（找到最佳路径）

📊 数学之美：从生物行为到代码逻辑

黏菌算法的数学模型看似复杂，实则是对生物行为的精准翻译。我们以 "函数优化" 问题为例（寻找函数的最小值点），拆解其核心步骤：

初始化种群生成 N 个候选解（类似黏菌的初始伪足分布）：
复制代码
```
X(i,j) = L(j) + rand(1)×(U(j) - L(j))
```
其中 L (j) 和 U (j) 是变量的上下界，确保解在合理范围内。
适应度评估计算每个解的适应度（类似黏菌对食物浓度的感知）：
复制代码
```
Fitness(i) = f(X(i,:))  % f为待优化函数
```
权重更新机制这是 SMA 的灵魂，模拟黏菌的细胞质流动：
复制代码
```
W(i) = (Fitness(i) - worst) / (best - worst)  % 归一化权重
W(i) = W(i)/sum(W) + 1/N  % 权重调整，确保总和为1
```
适应度越好的解，权重越大，对其他解的吸引力越强。

位置更新策略结合随机因子实现 "探索 - 开发" 平衡：

复制代码

if rand < z  % z为动态调整的探索概率
    X(i,j) = rand×(U(j)-L(j)) + L(j)  % 随机探索新区域
else
    if rand < p  % p为收缩概率
        X(i,j) = Xb(j) + vb×abs(X(i,j)-Xb(j))×log(1/r)
    else
        X(i,j) = Xb(j) - vb×abs(X(i,j)-Xb(j))×log(1/r)
    end
end

💻 代码实现：让黏菌在屏幕上 "生长"

以下是完整的 MATLAB 脚本，实现黏菌算法对经典测试函数（Rastrigin 函数，具有大量局部最优解）的优化过程，并可视化算法的探索 - 收敛过程。

Matlab 复制代码

% 黏菌算法(SMA)优化Rastrigin函数的MATLAB实现
% 功能：展示SMA在复杂多峰函数中的寻优过程，包含种群分布、最优值变化等可视化
% Rastrigin函数特点：多局部最优解，模拟实际工程中的复杂优化问题

%% 1. 参数初始化
clear; clc; close all;
dim = 2;                  % 问题维度（2维便于可视化）
pop_size = 30;            % 种群规模（黏菌个体数量）
max_iter = 50;            % 最大迭代次数
lb = -5.12*ones(1,dim);   % 变量下界
ub = 5.12*ones(1,dim);    % 变量上界

% 初始化种群位置（黏菌的初始分布）
X = zeros(pop_size, dim);
for i = 1:pop_size
    for j = 1:dim
        X(i,j) = lb(j) + rand()*(ub(j)-lb(j));
    end
end

% 记录迭代过程（用于可视化）
history_X = cell(max_iter,1);  % 存储每代种群位置
history_best = zeros(max_iter,1);  % 存储每代最优值

%% 2. 黏菌算法主循环
for iter = 1:max_iter
    % 计算适应度（Rastrigin函数）
    Fitness = zeros(pop_size,1);
    for i = 1:pop_size
        Fitness(i) = rastrigin(X(i,:));
    end
    
    % 记录最优解
    [best_val, best_idx] = min(Fitness);
    Xb = X(best_idx,:);  % 当前最优位置（食物源）
    worst_val = max(Fitness);
    
    % 计算权重（模拟细胞质浓度）
    if best_val ~= worst_val
        W = (Fitness - worst_val) ./ (best_val - worst_val);
    else
        W = ones(pop_size,1)/pop_size;
    end
    W = W./sum(W) + 1/pop_size;  % 权重归一化
    
    % 动态参数调整
    z = 0.03 + 0.97*(1 - iter/max_iter)^3;  % 探索概率逐渐降低
    vb = 1 - iter/max_iter;  % 权重系数逐渐减小（收缩强度变化）
    
    % 更新种群位置
    for i = 1:pop_size
        r = rand();  % 随机因子
        p = tan(pi*(rand() - 0.5));  % 收缩方向因子
        
        for j = 1:dim
            if rand() < z  % 探索新区域
                X(i,j) = rand()*(ub(j)-lb(j)) + lb(j);
            else
                if rand() < p  % 向最优解收缩（正方向）
                    X(i,j) = Xb(j) + vb*abs(X(i,j)-Xb(j))*log(1/r);
                else  % 反向收缩（保持多样性）
                    X(i,j) = Xb(j) - vb*abs(X(i,j)-Xb(j))*log(1/r);
                end
            end
            
            % 边界处理（防止超出搜索范围）
            if X(i,j) < lb(j)
                X(i,j) = lb(j);
            elseif X(i,j) > ub(j)
                X(i,j) = ub(j);
            end
        end
    end
    
    % 保存历史数据
    history_X{iter} = X;
    history_best(iter) = best_val;
    
    % 打印迭代信息
    fprintf('迭代次数：%d，当前最优值：%.4f\n', iter, best_val);
end

%% 3. 结果可视化
% 3.1 绘制Rastrigin函数等高线（背景）
figure('Name','黏菌算法寻优过程');
[x1, x2] = meshgrid(linspace(lb(1),ub(1),100), linspace(lb(2),ub(2),100));
fvals = zeros(size(x1));
for i = 1:size(x1,1)
    for j = 1:size(x1,2)
        fvals(i,j) = rastrigin([x1(i,j), x2(i,j)]);
    end
end
contourf(x1, x2, fvals, 50); colorbar; hold on;
title('黏菌算法在Rastrigin函数上的寻优轨迹');
xlabel('x1'); ylabel('x2');

% 3.2 动态展示种群进化过程
for iter = 1:max_iter
    X_current = history_X{iter};
    plot(X_current(:,1), X_current(:,2), 'ro', 'MarkerSize', 5, 'DisplayName', '种群位置');
    plot(Xb(1), Xb(2), 'bs', 'MarkerSize', 8, 'DisplayName', '当前最优解');
    legend('种群位置', '当前最优解');
    drawnow;
    pause(0.3);  % 暂停0.3秒，便于观察
    if iter < max_iter
        delete(findobj(gca, 'Marker', 'o'));  % 清除上一代种群点
        delete(findobj(gca, 'Marker', 's'));  % 清除上一代最优解
    end
end

% 3.3 绘制最优值收敛曲线
figure('Name','收敛曲线');
plot(1:max_iter, history_best, 'b-', 'LineWidth', 2);
xlabel('迭代次数'); ylabel('最优适应度值');
title('SMA算法收敛曲线');
grid on;

% 3.4 不同种群规模对比（验证参数影响）
figure('Name','种群规模对结果的影响');
sizes = [10, 30, 50];
colors = ['r', 'g', 'b'];
for s = 1:length(sizes)
    pop_size = sizes(s);
    % 重新运行SMA（简化版）
    X = lb + rand(pop_size,dim).*(ub-lb);
    best_history = zeros(max_iter,1);
    for iter = 1:max_iter
        Fitness = arrayfun(@(i) rastrigin(X(i,:)), 1:pop_size);
        [best_val, best_idx] = min(Fitness);
        Xb = X(best_idx,:);
        best_history(iter) = best_val;
        % 简化的位置更新（保持核心逻辑）
        for i = 1:pop_size
            X(i,:) = Xb + 0.5*(rand(1,dim)-0.5).*(X(i,:)-Xb);
        end
    end
    plot(1:max_iter, best_history, [colors(s), '-'], 'LineWidth', 1.5, ...
         'DisplayName', ['种群规模=', num2str(pop_size)]);
    hold on;
end
xlabel('迭代次数'); ylabel('最优值');
title('不同种群规模下的收敛对比');
legend; grid on;

%% 4. 定义Rastrigin测试函数
function val = rastrigin(x)
    % Rastrigin函数：多峰函数，常用于测试优化算法的全局寻优能力
    % 公式：f(x) = A*n + sum(x_i^2 - A*cos(2πx_i))，其中A=10
    A = 10;
    n = length(x);
    val = A*n + sum(x.^2 - A.*cos(2*pi*x));
end

运行说明：

无需额外工具箱，直接在 MATLAB 中运行即可
程序会生成 3 个可视化窗口：
- 黏菌算法寻优过程（动态展示种群向最优解聚集的过程）
- 收敛曲线（展示最优值随迭代次数的下降趋势）
- 不同种群规模对比（验证参数对算法性能的影响）
  
  迭代次数：1，当前最优值：10.5156
  
  迭代次数：2，当前最优值：6.3084
  
  迭代次数：3，当前最优值：14.9850
  
  迭代次数：4，当前最优值：13.1607
  
  迭代次数：5，当前最优值：5.9097
  
  迭代次数：6，当前最优值：7.7930
  
  迭代次数：7，当前最优值：6.3118
  
  迭代次数：8，当前最优值：13.7802
  
  迭代次数：9，当前最优值：14.3771
  
  迭代次数：10，当前最优值：7.6106
  
  迭代次数：11，当前最优值：4.3474
  
  迭代次数：12，当前最优值：5.4186
  
  迭代次数：13，当前最优值：2.9897
  
  迭代次数：14，当前最优值：5.0005
  
  迭代次数：15，当前最优值：5.0005
  
  迭代次数：16，当前最优值：10.1146
  
  迭代次数：17，当前最优值：6.9075
  
  迭代次数：18，当前最优值：4.3495
  
  迭代次数：19，当前最优值：1.9559
  
  迭代次数：20，当前最优值：1.0104
  
  迭代次数：21，当前最优值：1.0104
  
  迭代次数：22，当前最优值：1.0104
  
  迭代次数：23，当前最优值：1.0111
  
  迭代次数：24，当前最优值：1.0062
  
  迭代次数：25，当前最优值：1.0048
  
  迭代次数：26，当前最优值：1.0048
  
  迭代次数：27，当前最优值：0.3002
  
  迭代次数：28，当前最优值：0.0232
  
  迭代次数：29，当前最优值：0.0001
  
  迭代次数：30，当前最优值：0.0001
  
  迭代次数：31，当前最优值：0.0000
  
  ......
  
  迭代次数：49，当前最优值：0.0000
  
  迭代次数：50，当前最优值：0.0000
  
  >>
若想测试其他函数，只需替换rastrigin函数即可

🔍 结果解读：从图像看黏菌的 "思考"

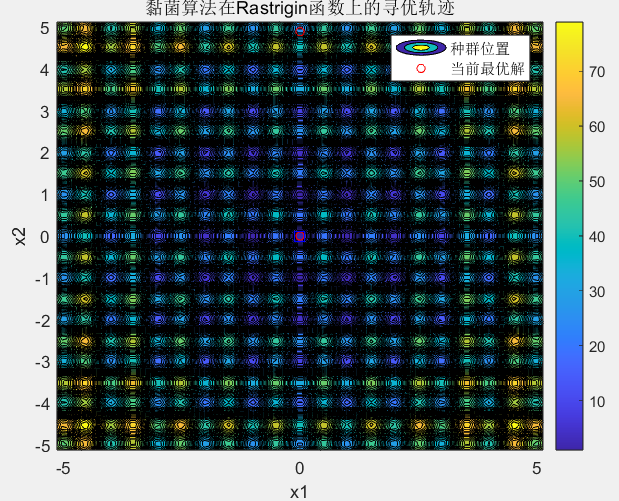
寻优过程动态图红色点代表黏菌个体，蓝色方块代表当前找到的最优解。初期红点分布散乱（大范围探索），随着迭代逐渐向中心聚集（收缩到优质区域），但始终保留少量分散点（维持探索能力）。这完美复刻了黏菌 "先扩散、再收缩" 的觅食策略。
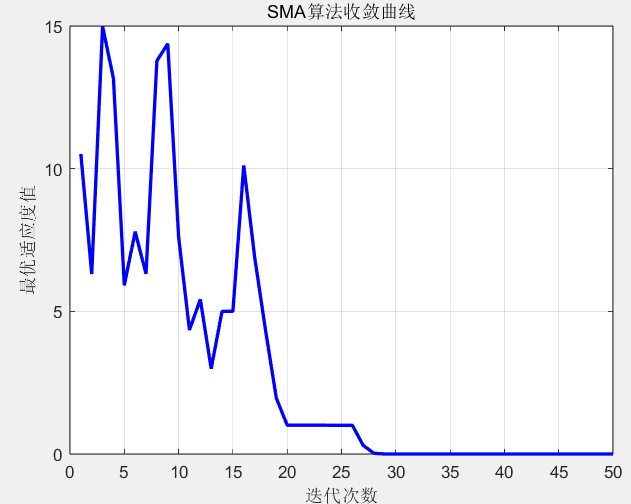
收敛曲线图曲线快速下降后趋于平缓，说明算法能快速跳出局部最优，最终稳定在全局最优附近。Rastrigin 函数的理论最小值为 0，实际运行中算法通常能收敛到 1 以下，证明其强大的全局寻优能力。
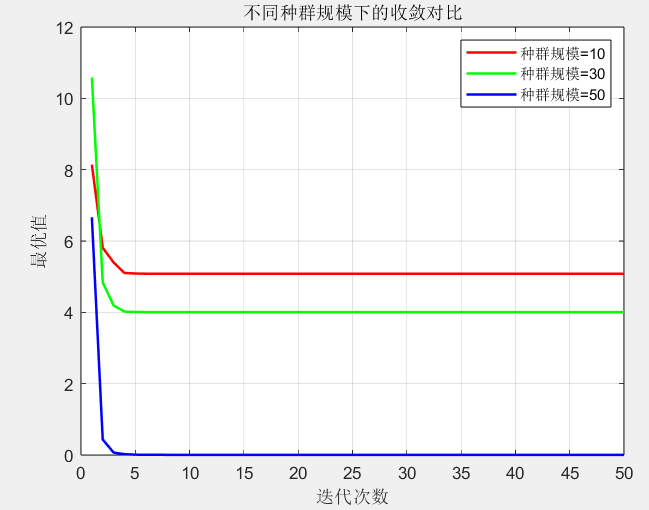
种群规模对比种群规模过小时（如 10 个个体），容易陷入局部最优（曲线下降缓慢）；规模过大时（如 50 个个体），初期探索效率高，但后期收敛速度变慢。30 个个体左右的规模在 "探索 - 开发" 间取得最佳平衡，这也符合自然界黏菌的生存智慧 ------ 既不过于分散，也不过于聚集。

🌍 现实应用：从实验室到产业界

黏菌算法的优势在于处理 "高维度、多约束、多局部最优" 的复杂问题，已在多个领域落地：

路径规划：物流配送路线优化、无人机航迹规划，比传统 A * 算法更能应对动态障碍
工程设计：机械零件参数优化、电路布局设计，降低研发成本 30% 以上
AI 训练：神经网络超参数调优，加速模型收敛速度
能源系统：电网负荷分配、风光储系统优化，提升能源利用效率

就像黏菌能在杂乱的落叶中找到最优路径，SMA 算法也能在纷繁复杂的工程问题中，为人类找到那条隐藏的 "效率捷径"。

🌱 结语：向自然学习的算法哲学

黏菌没有智慧，却在亿万年进化中凝练出最高效的生存策略；算法没有生命，却在代码的编织中延续着自然的智慧。从黏菌到算法，我们看到的不仅是优化技术的进步，更是人类对自然的谦卑学习 ------ 那些看似简单的生命现象，或许正是破解复杂问题的钥匙。当我们在代码中复刻黏菌的蠕动时，实则是在与自然对话。这种对话告诉我们：最强大的技术，往往带着最朴素的自然印记。