LeetCode(python)——73.矩阵置零

题目

给定一个 mxn 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用原地算法**。**

示例 1：

复制代码

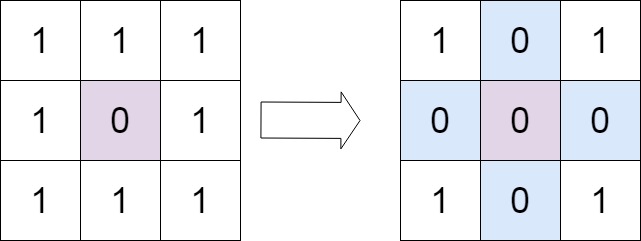
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

复制代码

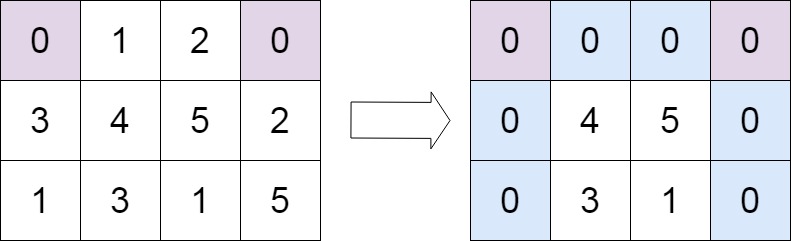
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

提示：

m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-231 <= matrix[i][j] <= 231 - 1

思路

1.非常直观的想法：遍历矩阵，用一个ans数组存矩阵中的零存在的位置，再遍历ans，找到对应行、列，置零------空间复杂度O(m*n）

2.优化：将ans拆分成两个数组：一个存需要置零的行，一个存需要置零的列，分别遍历这两个数组，将原数组置零------空间复杂度O(m + n)

3.优化：先单独处理原数组的第一行、第一列（用bool变量标识是否需要置零），再利用原数组的第一行和第一列存需要置零的行和列------空间复杂度O(1)

代码

python 复制代码

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        m = len(matrix)
        n = len(matrix[0])
        first_row = False   # 标识第一行、第一列是否需要置零
        first_col = False

        for i in range(m):
            if matrix[i][0] == 0:
                first_col = True
        for j in range(n):
            if matrix[0][j] == 0:
                first_row = True
        
        for i in range(1,m):   # 从第二行、第二列开始遍历数组
            for j in range(1,n):
                if matrix[i][j] == 0:
                    matrix[i][0] = 0   # 将需要置零的行、列分别存进第一列、第一行
                    matrix[0][j] = 0

        for j in range(1, n):   # 从第二行、第二列开始置零
            if matrix[0][j] == 0:
                for i in range(m):
                    matrix[i][j] = 0
        for i in range(1, m):
            if matrix[i][0] == 0:
                for j in range(n):
                    matrix[i][j] = 0
        if first_row:   # 单独处理第一行、第一列
            for j in range(n):
                matrix[0][j] = 0
        if first_col:
            for i in range(m):
                matrix[i][0] = 0